引言

磁共振成像（Magnetic Resonance Imaging, MRI）信号包含有幅值信息和相位信息.通常情况下，常规的MR成像方法大多利用幅值信息而忽略了相位信息.然而，磁共振信号的相位信息一样包含有丰富的信息.通过对获取的相位信息进行一定的预处理，我们可以获得反映组织局部磁场变化的信息，这种局部磁场变化主要由组织间的磁化率差异引起.磁化率是组织的一种内在性质，可以为临床医生提供一些相关疾病的重要的诊断信息.

磁化率加权成像（Susceptibility Weighted Imaging, SWI）是一种尝试通过采集组织的相关磁化率信息来获得脑疾病诊断信息的技术.该技术是近年来新开发的核磁共振（Nuclear Magnetic Resonance, NMR）对比增强成像技术，最早由E. Mark Haacke等人于1997年发明^[1].SWI基于组织间磁化率的差异，提供不同于质子密度、T₁及T₂加权的新型对比技术.在足够长的回波时间条件下，磁敏感区域的信号将与周围区域信号反相，因此相位图像可以提供一个新型对比增强技术.尤其在灰质与白质（GM/WM）、铁沉积组织、静脉血管以及其他磁敏感组织上，相位图像提供的对比更加明显^[2].SWI以梯度回波（Gradient Recalled-Echo, GRE）作为序列基础.在大量的神经系统诊断评估中，SWI可以提供更细节的临床信息，与常规MR成像序列相辅相成.

SWI自诞生之初就得到了快速发展，在临床医学上做出了很大的贡献.但不足之处是，SWI不能对组织内的磁化率信息进行定量分析.随着现代医疗科技的发展，只对组织内铁沉积等顺磁性物质做定性分析已经满足不了临床医学的需要，在SWI技术的基础上，21世纪初开始有学者提出对磁敏感性物质的磁化率做定量分析^[3-5]，即定量磁化率成像（Quantitative Susceptibility Mapping, QSM）.利用MRI方法获取磁化率定量图像，在临床和前临床研究^[6-9]中可以提供一种非创伤性手段，如检测白质束和皮层灰质中的髓鞘^{[6, 10-12]}、测量缺氧或功能退化血液中的铁含量、检测非氯化血红素铁沉积^[13-18]等.不仅如此，对组织内部顺磁性铁含量的测量，有利于对动脉血氧合水平和器官（如肝脏和心脏）内铁负载的评估，也有利于对脑部血管疾病和神经病变疾病的诊断和监控^[19].在这些巨大潜力的优势下，QSM在科学研究和临床应用上得到了快速发展.

同SWI一样，QSM也以梯度回波作为序列基础，并同样需要对相位信息进行一定的预处理，包括对相位信息进行解缠绕及去除背景场处理，以获得反映局部磁场变化的场图.不同之处在于，QSM需要结合特有的重建算法，根据处理后的场图信息重建出磁化率图像.组织的局部磁化率差异会引起组织周围场的差异并对MR信号产生影响.假设沿z方向施加一个外磁场B₀，样品在该磁场下的磁化率分布为${\boldsymbol{\chi }}\left( {\boldsymbol{r}} \right)$，那么：

$\delta B\left( \boldsymbol{r} \right) = \delta \left( \boldsymbol{r} \right){B_0} = {B_0}\int\limits_{\boldsymbol{r}' \ne \boldsymbol{r}} {\chi \left( {\boldsymbol{r}'} \right)\frac{{3{{\cos }^2}\left( {{\theta _{rr'}}} \right) - 1}}{{4\pi {{\left| {\boldsymbol{r}' - \boldsymbol{r}} \right|}^3}}}{{\text{d}}^3}r'} = {B_0}\left( {\boldsymbol{r} \otimes \boldsymbol{d}} \right)\left( \boldsymbol{r} \right)$ [19]

(1)

其中$\delta $为标准域变换，θ_rr'是B₀与r'-r的相角，$\delta B\left( r \right)$表示由B₀引起的变化.由（1）式可以看出，这个变化可以表示为磁化率分布与沿B₀向单元磁偶极子$d\left( \boldsymbol{r} \right)={\left( 3{{\cos }^{2}}\left( \theta \right)-1 \right)}/{4\pi {{\left| \boldsymbol{r} \right|}^{3}}}\;$的卷积，θ是B₀与r之间的角度.空间的积分运算在傅里叶变换域改写成乘积运算：

$\boldsymbol{B}\left( \boldsymbol{k} \right) = \boldsymbol{\chi} \left( \boldsymbol{k} \right) \cdot \left( {\frac{1}{3} - \frac{{k_z^2}}{{{k^2}}}} \right)$ [10]

(2)

其中k为傅氏域坐标.引入${{D}_{2}}\left( \boldsymbol{k} \right)=\left( {1}/{3}\;-{k_{z}^{2}}/{{{k}^{2}}}\; \right)$，其中$k={{\left( k_{x}^{2}+k_{y}^{2}+k_{z}^{2} \right)}^{{1}/{2}\;}}$，B(k)由回波时间（TE）内的相位偏移决定，反映了由磁化率分布决定的相位分布，属于相位的全局特征，受D₂(k)影响它的各向异性会变得明显.最后引入$\psi \left( \boldsymbol{k} \right){\boldsymbol{ = }}B\left( \boldsymbol{k} \right)/{B_0}$，可以得到：

$\boldsymbol{\psi} \left( \boldsymbol{k} \right){\boldsymbol{ = }}\boldsymbol{\chi} \left( \boldsymbol{k} \right) \cdot {\boldsymbol{D}_2}\left( \boldsymbol{k} \right)$ [10]

(3)

这里${\boldsymbol{\psi }}\left( {\boldsymbol{k}} \right)$和${\boldsymbol{\chi }}\left( {\boldsymbol{k}} \right)$分别是${\boldsymbol{\psi }}\left( {\boldsymbol{r}} \right)$和${\boldsymbol{\chi }}\left( {\boldsymbol{r}} \right)$的傅立叶变换.通过频移变换可以得到：

$\boldsymbol{\chi} \left( \boldsymbol{k} \right){\boldsymbol{ = }}\boldsymbol{\psi} \left( \boldsymbol{k} \right) \cdot {\boldsymbol{D}_2}{\left( \boldsymbol{k} \right)^{ - 1}}$ [10]

(4)

显然，这种${\boldsymbol{\chi }}\left( {\boldsymbol{k}} \right)$的求解形式要比积分形式简单得多.然而，频域中定义的圆锥表面上存在${\boldsymbol{D}_2}\left( \boldsymbol{k} \right) = 0$的点，直接求解${\boldsymbol{D}_2}{\left( \boldsymbol{k} \right)^{ - 1}}$并不可行.因此，如何在求解过程中避免${\boldsymbol{D}_2}\left( \boldsymbol{k} \right) = 0$的点成为求解磁化率分布${\boldsymbol{\chi }}\left( {\boldsymbol{k}} \right)$的关键，也是QSM图像重建算法的关键.

由(4)式我们可以获知，通过测量得到的磁场来求解任意磁化率分布，本质上是不适定的.那么，如何求解不适定逆问题成为QSM技术的关键，也成为QSM研究领域的一个关键问题.本文将首先介绍两种目前使用较广泛的去除背景场方法，接着介绍3种最具有代表性的QSM重建方法，以及QSM在MRI中的应用，并对QSM的未来发展前景进行展望.

1 去除背景场方法

在MRI中，包括匀场不完全及组织与空气交界的磁化率变化在内的多种因素，均可能导致强烈的背景场变化.大量背景场相位的存在不仅掩盖了局部组织对比度，还使本来不理想的相位缠绕变得更差.如果计算磁化率分布前没有去除背景场相位的影响，会导致严重的磁化率计算错误.为了获得高质量的SWI和QSM，首先要做的就是，区分出背景场与这些局部磁化率产生的局部磁场.对于SWI来说，由于无需进行反演重建，简单的高通滤波已经足够.然而，对于QSM来说，在病态逆问题的求解情况下，背景场去除效果不理想会对磁化率的求解产生较大影响，甚至会导致最终的磁化率成像结果不可用.因此，QSM技术的出现对背景场的去除提出了更高的要求.本文将介绍两种目前去除背景场效果最好的方法：复杂谐波伪影去除法（Sophisticated Harmonic Artifact Reduction for Phase data, SHARP）^[16]和偶极场投影法（Projection onto Dipole Fields, PDF）^[20].

1.1 复杂谐波伪影去除法--SHARP

复杂谐波伪影去除法SHARP由德国的Schweser F小组在2011年提出^[16].该方法认为磁场扰动由外部磁场扰动（External Magnetic Field Perturbations, EMP）和内部磁场扰动（Internal Magnetic Field Perturbations, IMP）^[21]共同构成，EMP由兴趣体积（Volume of Interest, VOI）外的磁化源产生，IMP由VOI内的磁化源产生，而只有内部磁场扰动${{\boldsymbol{B}}_{\operatorname{int} }}$才会决定磁化率分布${\boldsymbol{\chi }}\left( {\boldsymbol{r}} \right)$.EMP在整个VOI内具有谐波性质，因此满足拉普拉斯方程${\nabla ^2}{{\boldsymbol{B}}_{ext}} = 0$^{[3, 22]}，IMP在整个VOI内不具有谐波性质，因此可以利用这个区别将IMP从磁场扰动中提取出来.首先对总磁场扰动${{\boldsymbol{B}}^\Delta } = {{\boldsymbol{B}}_{ext}} + {{\boldsymbol{B}}_{\operatorname{int} }}$实施拉普拉斯方程可以得到：${\nabla ^2}{{\boldsymbol{B}}^\Delta } = {\nabla ^2}{{\boldsymbol{B}}_{\operatorname{int} }}$，然后引入谐波均值理论来求解方程${{\boldsymbol{B}}_{\operatorname{int} }}$.谐波均值理论指一个均值函数${{\boldsymbol{B}}_{\operatorname{int} }}$与非负的径向对称的标准化函数$u\left( {\boldsymbol{r}} \right)$的卷积等于它本身，即$u\left( {\boldsymbol{r}} \right) = \left( {\rho \otimes u} \right)\left( {\boldsymbol{r}} \right)$.因此，利用${{\boldsymbol{B}}_{ext}}$的谐波均值性质可以消除磁场扰动${{\boldsymbol{B}}^\Delta }$中的EMP，得到：

${B_{\operatorname{int} }} = \left( {\delta - \rho } \right){ \otimes ^{ - 1}}{\hat B^\Delta }$ [16]

(5)

(5)式中$\delta $是位于径向函数中心的单位脉冲，这样，就可以通过去卷积（${ \otimes ^{ - 1}}$）把${{\boldsymbol{B}}_{\operatorname{int} }}$从过渡数据${\hat B^\Delta }$中重建出来.

SHARP算法在处理相位数据的同时也结合了幅值数据，利用脑部提取工具和二进制侵蚀操作，从幅值数据中得到一张侵蚀掩膜，这张掩膜与数据集$\left( {\delta - \rho } \right){ \otimes ^{ - 1}}{\hat B^\Delta }$相乘最后得到${{\boldsymbol{B}}_{\operatorname{int} }}$.SHARP算法的运行环境为MATLAB（Ver. 2010a），在16 GB RAM的双处理器工作站（Quad-Core Xeon L5430, Intel, Santa Clara, CA）上，处理数据集的时间范围为30 s~120 s.由于其他方法大多采用内部频率偏移（Internal Frequency Shift, IFS），而不是IMP来呈现最后结果，为了更好地与其他方法的结果比较，最后将IMP转化为IFS：${{\boldsymbol{f}}_{\operatorname{int}}}\left( \boldsymbol{r} \right)=-{\gamma {{\boldsymbol{B}}_{\operatorname{int}}}\left( \boldsymbol{r} \right)}/{2\pi }\;$.

图 1展示了使用SHARP算法得到的大脑组织的IFS图像.SHARP算法计算时，将大脑组织外的相位值置为0来避免不可靠的相位数据.IFS图像清晰地反映出了大脑磁化率分布的非局部性，图中可以清楚地看到很多大脑组织结构，如齿状核[图 1(c)]、基底神经节的子结构[图 1(d)]以及灰白质[图 1(e)].这些大脑中的顺磁性组织，都显示出了与周围组织不同的对比度，有利于临床诊断.可以看出，SHARP算法在保持VOI内部有用信息的同时，去除了叠加在VOI内部的外部磁场扰动.此外，SHARP算法具有较短的计算时间和较低的数学复杂度，在目前是一个具有优势的去除背景场方法.

1.2 偶极场投影法--PDF

偶极场投影法是由美国王乙小组于2011年所提出的^[20].该方法认为背景场主要由不均匀场和兴趣区（Region of Interest, ROI）外的磁化源引起，因此在一个特定有限空间内分离局部场和背景场非常困难，往往会导致对局部场的错误估计.同时，给定ROI的背景磁化源的先验知识，常常很难精确地得到，尤其在图像视野（Field of View, FOV）外存在磁化源的时候，会导致背景场无法完全去除.最可靠的去除背景场方法是使用扫描参考物法，即扫描一个跟样品完全相同，但没有磁化率变化的样品来计算出参考背景场^{[7, 15]}，但这在活体实验中是不可实现的.王乙小组率先发现除了边界处的局部偶极场，ROI外的偶极背景场与ROI内的局部偶极场在ROI内的内积接近于0这一现象.基于此特性他们提出了偶极场投影法来分离局部场和背景场，并取得了较好的效果.

在给定的ROI中，局部场${{\boldsymbol{f}}_L}$定义为：ROI内M的磁化率分布${{\boldsymbol{\chi }}_L}$产生的磁场，背景场${{\boldsymbol{f}}_B}$为FOV中ROI外$\bar M$的磁化率分布${{\boldsymbol{\chi }}_B}$产生的磁场.值得注意的是，背景场可以延伸到ROI内，局部场也可延伸到ROI外.PDF方法的目的，是把所有ROI内的测量磁场投影到包含所有背景场单位偶极场的子空间上，这由Hilbert空间的投影定理启发而得.PDF法来估计背景场的核心为：

$\arg \min {{\boldsymbol{\chi }}_{B \in \overline M }}{\left\| {{\boldsymbol{f}} - {\boldsymbol{d}} \otimes {{\boldsymbol{\chi }}_B}} \right\|_2}$ 20

(6)

一般情况下，正交需要满足：对于每一个局部单位偶极子场，它与任意背景场单位偶极子场的内积都为0.于是，PDF方法定义一个相关量$c\left( {{r_L}} \right)$，由位于任意位置${{\boldsymbol{r}}_L} \in M$的单位偶极子产生的局部场与任意背景单位偶极子场标准化内积的最大绝对值决定：

$0\le c\left( {{r}_{L}} \right)={{\max }_{{{r}_{B\in \overline{M}}}}}\left| {\left\langle {{d}_{{{r}_{L}}}},{{d}_{{{r}_{B}}}} \right\rangle }/{\left( {{\left\| {{d}_{{{r}_{L}}}} \right\|}_{2}}\times {{\left\| {{d}_{{{r}_{B}}}} \right\|}_{2}} \right)}\; \right|\le 1$ 20

(7)

(7)式中$c\left( {{r_L}} \right)$满足远远 < 1时认为背景场子空间与局部场子空间满足正交性.对一个真实脑部扫描图的典型脑部ROI进行分段评估后，除了位于边界处的5个体素[图 2(a)~(c)]，其他体素$c\left( {{r_L}} \right)$的最大绝对值几乎为都$0[c\left( {{r}_{L}} \right)\ll 0.1]$，因此近似认为背景场子空间与局部场子空间的正交性可以得到比较好的区分结果.

为了验证PDF方法的可行性，将PDF方法同高通滤波法（High-Pass Filtering，HPF）一起应用到脑部出血症病人的MRI图像中（图 3）.与PDF方法计算出的局部场[图 3(f)]相比，用HPF方法得到的局部场在脑部ROI外围包含较多的对病情诊断无用的场变化，推断是由空气-组织交界面引起的高频残余背景场[图 3(h)，白色箭头处]，很明显，PDF方法在空气-组织交界面的处理结果相比于HPF方法具有更少的伪影.不仅如此，PDF方法更好地刻画了出血病变，由出血症状引起的局部场比HPF方法得到的局部场更强[图 3(f), (h)黑色箭头处]，在局部场图中提供了更好的对比度.

2 QSM重建方法

众所周知，由场图信息重建磁化率图像是一个不适定逆问题，如何求解稳定解，并且对磁化率精确定量，成为QSM技术的关键.常用的QSM重建方法有Wharton S等人提出的k空间阈值分割法（Threshold-based k-space Division，TKD）、王乙小组提出的多方向采样磁化率计算方法^[15]、MEDI方法（Morphology Enabled Dipole Inversion，MEDI）和贝叶斯正则化方法^[19]，以及刘春雷小组提出的k空间加权微分法^[10].下面将介绍其中3种QSM重建算法：多方向采样磁化率计算方法、贝叶斯正则化方法和k空间加权微分法.

2.1 多方向采样磁化率计算方法--COSMOS

COSMOS（Calculation of Susceptibility Through Multiple Orientation Sampling）方法是指通过多方向抽样来计算磁化率^[15].COSMOS方法的中心思想为：首先关于极化场B₀对由磁化率分布引起的感应场进行多方向抽样，然后采用线性加权最小二乘法来计算出场噪声和无信号区域，最后重建出磁化率图像.下面将对逆问题的不适定性进行本质分析，详细介绍关于B₀多方向抽样计算磁化率的方法，即COSMOS方法.

该小节中没有特殊说明的磁化率都是指体积磁化率.在求解引言中(2)式的逆问题时，COSMOS方法提出通过将样品关于主磁场旋转并且多次采样来求解磁化率分布.图 4对此作了直观解释，在两次扫描位置的相交处形成两组相对的锥面，由于锥面的顶角都 > 90°(54.7×2)，在这两组相对锥面上会形成截断，存在公零点线，因此要通过第3次扫描来避开零值点线.

在分析离散逆问题的误差传播时，需要用到条件数.条件数直接决定了绝对误差传播的上限，为了得到好的效果，要尽量使矩阵的条件数最小.那么对于特定采样方向$\left\{ {{\theta _n}} \right\},{\kern 1pt} \,n = 1,2, \cdots ,N$的条件数为：

${\kappa _{{\theta _1},{\theta _2}, \ldots ,{\theta _N}}} = \frac{{\mathop {\max }\limits_{{k_x},{k_y},{k_z}} \sqrt {{{\sum\limits_{i = 1}^N {\left[ {\frac{1}{3} - \frac{{{{\left( {{k_z}\cos {\theta _i} + {k_y}\sin {\theta _i}} \right)}^2}}}{{{k^2}}}} \right]} }^2}} }}{{\mathop {\min }\limits_{{k_x},{k_y},{k_z}} \sqrt {{{\sum\limits_{i = 1}^N {\left[ {\frac{1}{3} - \frac{{{{\left( {{k_z}\cos {\theta _i} + {k_y}\sin {\theta _i}} \right)}^2}}}{{{k^2}}}} \right]} }^2}} }}$ [15]

(8)

最佳采样方向为$\left\{ {\theta _n^*} \right\} = \arg {\min _{\left\{ {\theta _n^{}} \right\},n = 1,2, \cdots ,N}}{\kappa _{{\theta _1},{\theta _2}, \cdots ,{\theta _N}}},\;n = 1,2, \cdots ,N$.

找到最佳采样方向后，利用最小二乘法对后期数据进行QSM重建可以得到磁化率分布图像.下面将展示并讨论模拟和模型实验结果.对于模拟数据来说，最小条件数为2.031，相应的最佳采样方向为0°、60°、120°.图 5为模拟数据的处理结果，图 5(d)种没有出现魔角旋转磁化率重建法中常见的分散条状伪影，说明3个方向旋转采样可以更好地重建出原始磁化率分布.重建的磁化率与真实磁化率误差的平均值为$4.627{\text{ }}2{{\text{e}}^{ - 3}}$，相对于真实磁化率值来说是可忽略的.

MRI模型采用的是不同浓度的钆对比剂，图 6展示了钆-水模型的结果，并且给出了磁化率计算值与磁化率期望值的关系[图 6(d)]，获得了合理的磁化率估计（斜率为0.96，≈1），与线性模型（R²=0.999 7）的拟合度很高.图 6(b)为测量得到的场偏移，在钆对比剂管附近可以明显地看到偶极子模式，灰色箭头所指处出现很强的噪声，包括背景噪声和玻璃壁噪声.图 6(c)展示了由COSMOS方法得到磁化率重建图像，不同浓度的钆对比剂具有不同大小的磁化率分布，并且没有出现条状伪影.

总体上说，COSMOS在有噪声的情况下压制了常见的条状伪影，关于钆对比剂产生了正对比度，提供了一个稳定的磁化率定量方法.随着磁性纳米粒子在细胞疗法中的应用，这无疑将有利于细胞追踪技术的发展.由局部磁性纳米粒子产生的T₂^*效应，也已经用来实现纳米粒子的可视研究，但这种对比度常常被误认为是伪影，因此COSMOS方法对组织任意磁化率分布的定量能力将极大地促进QSM的发展.然而，COSMOS最大的问题是其在临床应用中会受到极大的限制，由于成像仪器腔体的限制，同时再考虑病人舒适角度，很难获得多个不同摆放方向的脑部成像.

2.2 贝叶斯正则化方法

贝叶斯正则化方法^[19]由美国王乙小组于2010年所提出，该方法从数学问题的矩阵解法入手，在求解磁化率重建的不适定逆问题之前利用贝叶斯统计为这个不适定逆问题找到一个最接近的先验概率，之后添加一个Tikhonov正则化项，再结合加权最小二乘法，共同求解磁化率分布.

一般而言，不同的体素具有任意不同的磁化率，那么一个位于r的体素就可以认为是一个具有强度$\chi \left( {\boldsymbol{r}} \right)$的磁偶极子.一个特定体素产生的频率响应就是所有体素的场偏移之和.可以用矩阵表示为${\boldsymbol{\delta }} = {\boldsymbol{C\chi }}$，${\boldsymbol{\delta }}$指标准化场移动的一个列向量，χ是磁化率列向量，C是由离散化卷积核$d\left( r \right)={\left[ 3{{\cos }^{2}}\left( \theta \right)-1 \right]}/{4\pi {{\left| r \right|}^{3}}}\;$得到的卷积矩阵.利用贝叶斯正则化方法求解磁化率分布的核心公式为：

${\min _{\boldsymbol{X}}}\left\| {{\boldsymbol{W}}\left( {{\boldsymbol{C\chi - \delta }}} \right)} \right\|_{\,2}^{\,2} + {\alpha ^2}\left\| {{{\boldsymbol{W}}_0}{\boldsymbol{\chi }}} \right\|_{\,2}^{\,2} + {\beta ^2}\left\| {{{\boldsymbol{W}}_1}{\boldsymbol{G\chi }}} \right\|_{\,2}^{\,2}$

(9)

(9)式中第一项是常规项，用来在最小二乘意义上保证采样数据的保真度.第二项的W₀为加权矩阵，与W类似也是一个对角矩阵，若一个区域内磁化率分布均匀，W₀对角线元素全为1，这时候将给出统一零解.求解这个偏微分方程类似于施加狄氏边界条件，这一项的相对影响受制于参数a.若W₀是一个单位矩阵，则相当于用标准Tikhonov正则化在小范数$\left\| {\boldsymbol{\chi }} \right\|_{{\kern 1pt} 2}^{}$条件下求解问题.最后一项与施加Neumann-like边界条件相似，采用渐变求解法.矩阵$G = [{G_x}{\kern 1pt} {\kern 1pt} {G_y}{\kern 1pt} {\kern 1pt} {G_z}]'$表示3个方向的梯度算子，β是相应的正则化参数.与w类似，${W_1}{\boldsymbol{ = }}[{W_{1x}}{\kern 1pt} {\kern 1pt} {W_{1y}}{\kern 1pt} {\kern 1pt} {W_{1z}}]$的每一个子阵都是对角阵，确保给定区域有平滑解.通常情况下，这个加权矩阵来自于MR幅值信号，目的是在一个平滑区域内得到与MR幅值信号匹配的解.

若W₁中的每一个子阵都是单位矩阵，则相当于在小范数$\left\| {{\boldsymbol{G\chi }}} \right\|_{{\kern 1pt} 2}^{}$条件下求解统一零梯度解.Berkin Bilgic等人^[23]提出将(9)式改写为：

${{\boldsymbol{\chi }}_{in}} = \arg {\min _{\boldsymbol{\chi }}}\left\| {{{\boldsymbol{\delta }}_{in}} - {\boldsymbol{C\chi }}} \right\|_{\,2}^{\,2} + {\boldsymbol{\lambda }}{\left\| {{\boldsymbol{G\chi }}} \right\|_{\,1}}$ [23]

(10)

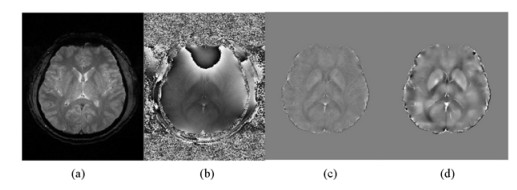
即l₁范数方法.其中下标in表示在ROI内，λ为正则化参数，保证数据一致性和空间平滑度.这个凸规划类似于压缩传感法（Compressed Sensing，CS）中为了在欠采样k空间数据中重建出MR图像而引入的目标函数.由CS理论可以知道，当欠采样数据在变换域近似稀疏时，可以利用非线性重建法从随机欠采的k空间数据中重建出图像.本研究小组利用l₁范数方法重建出了脑部磁化率分布图像[图 7(d)]，脑部图像来自于厦门大学附属中山医院.从图 7(d)中可以看到清晰的脑部解剖结构，并且在磁化率较强的位置具有较明显的对比度（如苍白球），这些细节信息在幅值图[图 7(a)]中是看不到的，由于存在大量的背景场影响，相位图[图 7(b)]也没有直观地显示出脑部细节信息.在局部场图[图 7(c)]和磁化率分布图中，ROI的边缘出现了计算噪声，但对ROI内部细节信息的影响不大.

下面将展示贝叶斯正则化方法在模拟及MRI模型实验上的应用.模拟模型的实验选用了4种不同正则化加权参数作对比，如表 1.每一种方法选择了3种噪声参数，即：0.1倍匹配噪声参数，匹配噪声参数和10倍匹配噪声参数，分别对应欠正则化，匹配参数正则化和过正则化，结果如图 8所示.图中可以看出，方法4得到的磁化率重现图像在4种方法中效果最好，其他3种方法的结果中出现了明显的由尖峰噪声引起的条纹伪影^{[24, 25]}，匹配噪声参数增大，这些伪影有所减弱，但同时降低了图像的清晰度.方法4对磁化率的重建图像并没有随着匹配噪声参数的变化发生明显变化，鲁棒性比较强.

MRI实验模型为不同浓度的钆对比剂组合模型，钆对比剂浓度依次为0.5%、1%、1.5%、2%、2.5%、3%，室温下各自的磁化率分别为0.81、1.63、2.45、3.26、4.08、4.89 ppm，利用这7种对比剂的磁化率，拟合出该浓度梯度下的磁化率斜率约为0.93.图 9展示了使用贝叶斯正则化方法对不同横截面的磁化率重建图像，钆对比剂管周围出现明显的偶极模式，并且相位值随对比剂浓度的增加而增大.图 9(c)、(g)为在匹配噪声参数下，贝叶斯方法重建出的磁化率图像，磁化率与匹配噪声的斜率为0.95.图 9(d)、(h)为10倍匹配噪声参数下贝叶斯方法重建出的磁化率图像，磁化率与匹配噪声的斜率为0.92.可以明显看出，随着参数增大，磁化率重建图像的清晰度变好，显示出极好的去噪能力.

综上所述，基于贝叶斯正则化的QSM方法可以精确地重建出磁化率图像，空间先验项提高了该不适定逆问题解的稳定性.正则化参数对实验结果的影响也在模拟及模型实验中得到验证.随着临床磁化率定量研究的发展，该方法将在磁性对比剂的定量中发挥极大的作用.

2.3 k空间加权微分法(WKD)

MRI采样中得到的大部分相位图像都含有噪声，缺少组织对比度，限制了相位图像在临床诊断上的应用.随着相位图像处理技术的发展及信噪比的改善，Rauscher^[26]提出相位图像可以提供极好的对比度，反映出组织结构，比如深核和白质结构，这些在幅值图像中是看不到的.由于相位对比度具有非局部性，并且依赖于方向，直接处理相位信息存在内在限制，因此可以先从组织的磁化率入手.基于这些考虑，Li Wei等人^[10]提出利用两个互补方程来消除锥面上的零值点：其一，相位与磁化率的傅立叶变换方程；其二，第一个方程在空间频域的一阶偏微分方程.

由于${\boldsymbol{D}_2}\left( \boldsymbol{k} \right)$在锥面上=0时它的一阶偏微分≠0，因此为了在锥面上求解磁化率分布${\boldsymbol{\chi }}\left( {\boldsymbol{k}} \right)$，可以先对引言中的(3)式在频域求一阶偏微分.利用梯度场计算${\boldsymbol{\chi }}\left( {\boldsymbol{k}} \right)$需要磁化率分布的频谱满足一阶可微，脑组织是空间连续的，且可以做傅立叶变换，因此满足上述条件.(3)式在频域关于k_z的一阶偏微分方程为：

$\chi \left( \boldsymbol{k} \right) \cdot {D_3}\left( \boldsymbol{k} \right) + FT\left[ {i{r_z}\chi \left( r \right)} \right] \cdot {\boldsymbol{D}_2}\left( \boldsymbol{k} \right) = FT\left[ {i{r_z}\psi \left( r \right)} \right]$ [10]

(11)

其中${D_3}\left( \boldsymbol{k} \right) = (k_x^2 + k_y^2)k_z^{}/\pi {k^4}$.在锥面附近，${\boldsymbol{D}_2}\left( \boldsymbol{k} \right)$值非常小，因此可以忽略$FT\left[ {i{r_z}\chi \left( r \right)} \right] \cdot {\boldsymbol{D}_2}\left( \boldsymbol{k} \right)$，这样，微分的非局部性质消除了(3)式中${\boldsymbol{D}_2}\left( \boldsymbol{k} \right)$的零值点.由于${D_3}\left( \boldsymbol{k} \right)$的值只有在锥面附近很大，因此(11)式的微分关系在k空间的锥面附近才成立.结合方程$\chi \left( \boldsymbol{k} \right){\boldsymbol{ = }}\psi \left( \boldsymbol{k} \right) \cdot {\boldsymbol{D}_2}{\left( \boldsymbol{k} \right)^{ - 1}}$可以得到：

$\chi \left( \boldsymbol{k} \right){\boldsymbol{ = }}\psi \left( \boldsymbol{k} \right) \cdot {\boldsymbol{D}_2}{\left( \boldsymbol{k} \right)^{ - 1}},{\text{ }}{\boldsymbol{D}_2}\left( \boldsymbol{k} \right) \geqslant \varepsilon $ [10]

(12)

$\chi \left( \boldsymbol{k} \right) \approx FT\left[ {i{r_z}\psi \left( r \right)} \right] \cdot {D_3}{\left( \boldsymbol{k} \right)^{ - 1}},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\boldsymbol{D}_2}\left( \boldsymbol{k} \right) < \varepsilon $ [10]

(13)

这里ε是预先确定的阈值.这种求解磁化率的方法叫做直接法.作为对比结果，同时也利用阈值法计算出了锥面附近的${\boldsymbol{\chi }}\left( {\boldsymbol{k}} \right)$，即用下式代替(13)式：

$\chi \left( \boldsymbol{k} \right){\boldsymbol{ = }}{\varepsilon ^{ - 1}}\psi \left( \boldsymbol{k} \right),{\text{ }}{\boldsymbol{D}_2}\left( \boldsymbol{k} \right) < \varepsilon $ [10]

(14)

值得注意的是，(12)和(13)式成立依赖于视野（Field of View，FOV）内的全部相位值都存在.因此在计算脑部图像的磁化率分布时，(3)和(11)式要修改为：

${M_{brain}} \cdot \psi \left( r \right){\boldsymbol{ = }}{M_{brain}} \cdot F{T^{ - 1}}\left[ {\chi \left( \boldsymbol{k} \right) \cdot {\boldsymbol{D}_2}\left( \boldsymbol{k} \right)} \right]$ [10]

(15)

$\begin{gathered} {M_{D3}} \cdot FT\left\{ {{M_{brain}} \times F{T^{ - 1}}\left\{ {\chi \left( \boldsymbol{k} \right) \cdot {D_3}\left( \boldsymbol{k} \right) + FT\left[ {i{r_z}\chi \left( r \right)} \right] \cdot {\boldsymbol{D}_2}\left( \boldsymbol{k} \right)} \right\}} \right\} \hfill \\ = {M_{D3}} \cdot FT\left[ {i{r_z}{M_{brain}}\psi \left( r \right)} \right]\, \hfill \\ \end{gathered} $ [10]

(16)

这里${{\boldsymbol{M}}_{brain}}$是一个组织为1，背景场为0的二元掩膜，${{\boldsymbol{M}}_{D{\text{3}}}}$为光滑加权函数，用来强调锥面附近的微分关系.

由于求解活体脑部的磁化率分布图像时引入了二元掩膜${{\boldsymbol{M}}_{brain}}$，直接法不再适用.Li Wei等人提出使用正交及上三角分解最小二乘法LSQR^[27]来求解，同时在(15)式两边同时乘上系数矩阵的共轭转置来稳定数值解，即${{\boldsymbol{C}}^T}{\boldsymbol{C}} \cdot {\boldsymbol{\chi }}\left( {\boldsymbol{r}} \right){\boldsymbol{ = }}{{\boldsymbol{C}}^T}{\boldsymbol{\psi }}\left( {\boldsymbol{r}} \right)$.这里矩阵C是(15)式中定义的相位与磁化率关系矩阵，称这种求解方法为k空间加权微分法（Weighted k-space Derivative，WKD）.为了评估(16)式中微分关系的影响，利用LSQR方法直接求解(15)式，得到磁化率分布图像作为WKD方法的对比结果.

数值模型由多个插在均匀背景场中的椭圆体组成，每个椭圆体的磁化率值分别为0、0.2、0.3、1 ppm.同时使用了直接法[图 10(d)]和阈值法[图 10(c)]来计算磁化率分布${\boldsymbol{\chi }}({\boldsymbol{r}})$，图 10为数学模型的磁化率重建图.X-Z截面图[图 10(a)]中出现了明显的偶极模式，在与主磁场方向垂直的X-Y截面图[图 10(b)]中没有出现.在区域放大的图像中可以看到，阈值法计算得到磁化率分布的频谱在锥面附近出现了不连续点，说明出现了计算错误，而这些不连续在直接法[图 10(d)]中没有观察到.图 10(e)、(g)和图 10(f)、(h)分别为利用阈值法和直接法计算得到的X-Y、X-Z截面的磁化率分布图，图 10(i)、(j)为在SNR=30时分别用阈值法和直接法计算得到的X-Y截面的磁化率分布图.可以很直观地看到，阈值法的计算结果中出现了明显的条状伪影，而直接法计算得到的磁化率分布图不论有没有噪声都没有出现条状伪影.

这里使用了两种方法来重建磁化率分布图，即WKD法和LSQR法，两种方法的结果展示在图 11中.图 11(a)、(e)分别为使用LSQR方法重建的X-Y、X-Z截面磁化率分布图，图 11(b)、(f)分别为使用WKD方法重建的X-Y、X-Z截面磁化率分布图. LSQR方法提供了比较高质量的磁化率分布图[图 11(a)、(e)]，图中没有看到明显的条状伪影.但不足之处是，在k空间图像[图 11(g)]中，LSQR方法在锥面附近出现了明显的信号不连续（白色箭头所指处），这是因为LSQR法需要牺牲这些锥面附近数据来提高结果的稳定性，在磁化率重建图中可能会引起被误认为局部相位信息的伪影，不利于临床诊断.而WKD方法恢复出了锥面附近的信号，这不仅提高了磁化率对比度，而且在磁化率分布图[图 11(f)]中可以得到更多的局部细节（白色箭头所指处）.

LSQR方法和WKD方法重建出的磁化率分布图都显示了脑组织的局部细节信息，并且没有出现明显的条状伪影.该方法的优势将在日常临床应用或者科学研究中展现更大的价值.值得注意的是，成像参数，比如场强、回波时间、翻转角和空间分辨率等，也会对相位处理和磁化率分布图的精度产生影响，这个方面还值得进一步的研究.

3 QSM在临床中的应用 3.1 QSM在检测大脑髓磷脂中的应用

神经轴突周围缠绕的多层磷髓鞘，对中枢神经系统的正常运行非常重要，异常的髓鞘形成会导致很多神经系统疾病和神经系统紊乱^[28-30].现有的工作表明，战栗鼠神经系统髓磷脂的缺失会大大降低白质轴突磁化率，导致白质与灰质之间磁化率对比的消失.美国杜克大学的刘春雷小组提出，利用QSM与扩散张量成像（Diffusion Tensor Imaging，DTI）结合^[31]，来检测战栗鼠与正常鼠大脑中的髓磷脂含量，证明了髓磷脂是大脑灰质与白质磁化率差异的主要来源.

图 12为正常鼠与战栗鼠大脑磁化率分布图与相位图的对比，并且展示了正常鼠与战栗鼠的电子显微镜图像.正常鼠的相位图[图 12(a)]显示出了明显的白质与灰质对比度，相应的磁化率分布图[图 12(b)]也看到了高对比度，这个对比度在战栗鼠中几乎消失[图 12(d)、(e)].正常鼠的电子显微镜图像[图 12(c)]中可以看到稠密的磷髓鞘，而在战栗鼠的电子显微镜图像[图 12(f)]中只看到稀疏的磷髓鞘.

图 13展示了正常鼠和战栗鼠大脑中3个ROI，脑室附近的白质[图 13(a)]、前连合[图 13(b)]和小脑[图 13(c)]的扩散张量图、磁化率分布图和相位图.图中FA为部分各向异性，ADC为表观扩散系数.在脑室的扩散张量图[图 13(a)]中，在脑脊液CSF与脑组织之间出现了模糊边界，但在磁化率分布图中得到了恢复.图 13(b)中的相位图和磁化率分布图相比于FA扩散张量图都显示出了更加明显的轮廓.在3个ROI中，定量磁化率图像都证明了战栗鼠大脑中髓磷脂的缺失.

刘春雷小组的工作，验证了髓磷脂的缺失会引起白质与灰质对比度的大大降低，这表明髓磷脂可能是引起大脑对比度的主要原因.同时显示了QSM在刻画组织特性时相对于相位图和幅值图的优势，并且指出白质与灰质的相对磁化率值在评估髓鞘形成的强度时是一个有用的内源性生物标记.

3.2 QSM在大脑出血病人中的应用

以贝叶斯正则化方法为例，展示QSM方法在大脑出血病人中的应用.图 14为来自两个大脑出血病人的脑部图像，其中前面3个层面来自病人1，后3层来自病人2.在T₂^*加权的幅值图像[图 14(a)~(f)]中可以看到明显的信号暗区，说明有海绵状血管畸形出血症状.图 14(g)~(l)为相应的SWI图像，图 14(m)~(r)为相应的局部场图，图 14(s)~(x)为相应的磁化率重建图像.图 14(n)中有一个很强的局部场变化，说明在该处磁化率变化剧烈，对于强畸形和弱畸形其相应的场偏移是正的，而临近体素的场偏移是负的，说明存在顺磁性物质.在场图中，除了出血区附近的不均匀场外，整个脑部都能看到清晰的结构细节信息，尤其在纹状体和苍白球[图 14(m)、(p)]，红核和黑质[图 14(n)、(p)]，小脑核[图 14(o)]以及侧脑室中的其他结构[图 14(r)]附近.

利用方法4得到的磁化率重建图像[图 14(s)~(x)]，在脑部的不同位置都可以观测到出血处呈现出亮斑，说明具有非常强顺磁性的脱氧血红蛋白和高铁血红蛋白.脑部较高位置的层面可以看到灰质和白质具有不同的磁化率，纹状体和苍白球也比周围的组织具有更强的顺磁性[图 14(s)、(v)箭头所指处]，同样可以看到红核和黑质也是顺磁性的[图 14(t)、(w)箭头所指处].图 14(u)中侧脑室的小脑核是顺磁的，同时在病人2的侧脑室中检测到抗磁性物质[图 14(x)箭头所指处]，推测可能是脉络出现了钙化现象.

贝叶斯正则化方法成功地从梯度回波图像中重建出了精确的磁化率图像.它利用了通常被忽略的相位信息，在利用加权最小二乘逆问题求解局部场时考虑进了噪声，并且在基于幅值信息计算磁化率时添加了空间先验.合理的先验可以充分地稳定之前提到的不适定逆问题.施加贝叶斯正则化时基于噪声信息自动地选择正则化参数，最后得到磁化率重建图像.这是一个新颖的基于体素的定量磁化率成像方法，适用于活体大脑成像.

3.3 QSM在大脑灰白质中的应用

由于大脑白质的磁化率是依赖于方向的^{[6, 32]}，多方向扫描的方法不适用于对大脑白质的研究.那么只能考虑使用单方向扫描的方法来研究大脑灰白质以及其他大脑结构.这里介绍k空间加权微分法（WKD）在大脑结构中的研究应用.众所周知，大脑内部部分结构的磁化率是与脑脊液（Cerebrospinal Fluid, CSF）相关的，如苍白球、红核、黑质等.表 2给出了部分脑解剖结构及它们相对脑脊液的磁化率值.图 15给出了大脑轴截面的幅值图、相位图与磁化率分布图.

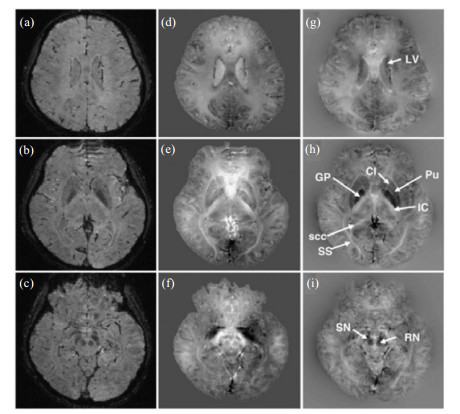
首先，磁化率分布图显示出了与相应的幅值图和相位图不一样的对比度.大脑中含铁量较多的结构，包括苍白球[图 15(h)]、红核和黑质[图 15(i)]等，相对于周围组织展示出了强烈的顺磁偏移.在相位图[图 15(e), (f)]中可以看到模糊的组织边界，表明了相位的非局部性质，另一方面，上面提到的大脑解剖结构都得到了准确的定位，说明定量磁化率分析具有明显的优势.不仅如此，磁化率分布图中大脑灰白质的对比度也很明显.图 15(h)中可以轻易地辨认出白质结构，如胼胝体压部、内囊以及矢状层等.在磁化率分布图中，矢状层部位比周围组织更亮，显示出较强的抗磁性，但在幅值图中的亮度较暗.其他结构，如红核、黑质和苍白球，在幅值图和磁化率分布图中也都显示了较暗的对比度.此外，从磁化率分布图中可以轻易地看到内囊[图 15(h)]，而在幅值图中是无法辨别的.图 15(g)还显示出了白质的磁化率不均匀性，这些不均匀性可能是由白质中的纤维束方向造成的.

大脑组织包含大量的可能会影响组织磁化率的分子混合物，比如非血红素铁，脱氧血红蛋白铁，髓磷脂和蛋白质等.WKD方法的结果表明，在铁含量丰富的结构，如大脑白质周围的红核、黑质、苍白球、齿状核等相对于CSF具有较强的顺磁偏移.铁含量的变化可能预示着神经系统疾病，如亨廷顿舞蹈病、帕金森病、阿耳滋海默氏病、多发性硬化以及慢性出血等^[33].WKD方法重建得到的磁化率分布图对白质的纤维束具有很强的识别能力，该方法可以作为一个精确的磁化率定量方法，应用到脑部铁离子定量和白质微结构的研究中.

4 总结与展望

QSM以梯度回波作为序列基础，对相位图像进行去除背景场处理后得到一张局部场分布图，结合特有的重建算法重建出磁化率图像.对组织内部顺磁性物质的定量评估，有利于大量脑血管疾病和神经病变疾病的诊断和监控.一个优秀的QSM算法可以实现对任意磁化率分布的重建，并且提供精确的磁化率定量和丰富的局部细节信息.目前的QSM算法已经应用到活体大脑中，并且有很好的表现，QSM技术在神经系统疾病等微结构病变上的应用，将是其未来的发展方向之一.