文章信息
- 张宗富, 肖立志, 刘化冰, 李新, 邓峰, 许巍, 安天琳, 成家杰
- ZHANG Zong-fu, XIAO Li-zhi, LIU Hua-bing, LI Xin, DENG Feng, XU Wei, AN Tian-lin, CHENG Jia-jie
- 水分子在微孔隙介质中的受限扩散模拟
- Simulation of Restricted Diffusion of Water Molecules in Micropores
- 波谱学杂志, 2014, 31(1): 49-60
- Chinese Journal of Magnetic Resonance, 2014, 31(1): 49-60
-
文章历史
收稿日期: 2012-12-12
收修改稿日期: 2012-12-29


核磁共振技术可以应用在石油测井行业[1, 2],来研究岩石的孔隙结构[3, 4]、油水饱和度、及渗透率等岩石物理性质[5].二维扩散-弛豫核磁共振[6]技术可以进行流体类型的识别和饱和度的计算.其中,流体的扩散系数作用重大,其值大小与流体类型相关.Song等人[3]利用内部梯度场中的扩散信息进行孔隙尺寸和孔隙连通性的判别.
岩石中的流体由于受到固体骨架的影响,其分子的扩散运动为受限扩散,其表观扩散系数小于流体的自由扩散系数,因此,在二维核磁共振测井及岩石物理实验中,利用扩散系数对数平均值[7]求取的油水饱和度会产生偏差;同时,受限扩散特征曲线能提供丰富的岩石物理信息,Zielinski等人[8]利用较短回波间隔的CPMG脉冲序列来探测更小尺寸的岩石孔隙,Kadayam Viswanathan等人[9]利用高压探测到了页岩气中的气体运动特征,并用此来进行微小孔隙的计算.
本文简述了受限扩散理论;介绍了有限差分和蒙特卡洛随机游走两种数值模拟方法;利用3种核磁共振脉冲梯度序列对单孔隙模型(平行板状、圆柱状、球形)模拟,并与前人对Bloch方程的解析解进行对比,得到两种模拟方法的优缺点及解析方法的准确度对比;建立球形周期性堆积模型、随机堆积模型,并对水分子在这两种连通多孔介质中的受限扩散曲线变化进行分析,由此来指导实际生产.
1 受限扩散理论分子自由扩散为随机的布朗运动,其均方根位移由爱因斯坦方程决定:
| $ \left\langle {{{\left[{r\left( t \right)-r\left( 0 \right)} \right]}^2}} \right\rangle = 6{D_0}t $ | (1) |
其中,r(t)表示任意t时刻分子的位置,D0为分子的自由扩散系数.
然而,在岩石中的流体由于受到骨架的影响,其分子运动为受限扩散,其表观扩散系数表达式由Sen等人[10]提出:
| $ D\left( t \right) = \frac{{\left\langle {{{\left[{r\left( t \right)-r\left( 0 \right)} \right]}^2}} \right\rangle }}{{6t}} $ | (2) |
当扩散时间td较短的时候,只有孔壁表面厚度为(D0td)1/2的分子受到受限扩散的影响,此时的表观扩散系数表达式[11]为:
| $ D\left( {{t_{\rm{d}}}} \right) = {D_0}\left[{1-\frac{4}{{9\sqrt \pi }}\;\frac{{S\sqrt {{D_0}{t_{\rm{d}}}} }}{V} + O\left( {{D_0}{t_{\rm{d}}}} \right)} \right] $ | (3) |
(3)式中S为孔隙表面积,V为孔隙体积,S/V则表征孔隙尺寸,O(D0td)表示比D0td高阶的无穷小量.D(td)与S/V成正比,因此,通过短时扩散系数的衰减曲线,可以求取孔隙尺寸的平均值[12].
当扩散时间td很长的时候,其表观扩散系数逐渐趋近一个常数[11],其表达式为:
| $ \mathop {\lim }\limits_{{t_{\rm{d}}} \to \infty } \frac{{D\left( {{t_{\rm{d}}}} \right)}}{{{D_0}}} = \frac{1}{{F\varphi }} \equiv \frac{1}{{{\tau _r}}} $ | (4) |
(4)式中F,φ,τr分别表示电法测井中的地层因子,孔隙度和弯曲度.利用长时扩散系数的渐进值可以确定孔隙的连通性.
2 数值模拟方法简介在多孔介质核磁共振实验中,分子磁化矢量衰减遵循的是Bloch-Torrey[13]方程:
| $ \frac{{\partial M\left( {r, t} \right)}}{{\partial t}} = {D_0}{\nabla ^2}M\left( {r, t} \right)-{\rm{i}}\gamma {B_z}\left( r \right)M\left( {r, t} \right)-\frac{{M\left( {r, t} \right)}}{{{T_2}}} $ | (5) |
边界条件为:
| $ D\frac{{\partial M\left( {r, t} \right)}}{{\partial v}} + \rho M\left( {r, t} \right) = 0 $ | (6) |
(6)式中,ρ为表面弛豫率,M(r, t)表示磁化矢量,γ为质子的旋磁比,Bz为静磁场,T2为横向弛豫时间,r为方向矢量.
2.1 有限差分方法(5)式为热传导方程的一个特例,因此可利用有限差分方法[14]进行数值求解.式中自由弛豫率1/T2与孔隙形态无关,只与流体分子的类型有关,且该值相对较小,因此,(5)式中最后一项不予以考虑.
如图 1所示,扩散沿着x轴,范围为-a/2 < x < a/2,其孔隙尺寸大小,即板间距为a,把板距分成N等份,间隔Δx=a/(N-1),则第j个位置的坐标xj=(j-1)×Δx-a/2,其中j=1,2,3,…,N.所对应的扩散时间的微分Δt=(Δx)2/2/D0,其满足爱因斯坦的扩散方程.因此,(5)式中的二阶导数可以表示为:
|
| 图 1 平行板模型有限差分示意图 Fig. 1 Graphical illustration of finite difference in slab model |
| $ {\nabla ^2}M\left( {x, t} \right) = \frac{{{\partial ^2}M\left( {x, t} \right)}}{{\partial {x^2}}}\left| {_{{x_j}} \to \frac{{M\left( {{x_{j + 1}}, t} \right)-2M\left( {{x_j}, t} \right) + M\left( {{x_{j-1}}, t} \right)}}{{{{\left( {\Delta x} \right)}^2}}}} \right. $ | (7) |
在上下两个边界上,其磁化矢量的衰减遵循(6)式,因此,其差分为:
| $ \begin{array}{l} \frac{{{\partial ^2}M\left( {x, t} \right)}}{{\partial {x^2}}}\left| {_{{x_i}}} \right. \to \frac{{M\left( {{x_2}, t} \right)-M\left( {{x_1}, t} \right)-\Delta x \cdot \rho /{D_0}}}{{{{\left( {\Delta x} \right)}^2}}}\\ \frac{{{\partial ^2}M\left( {x, t} \right)}}{{\partial {x^2}}}\left| {_{{x_N}}} \right. \to \frac{{M\left( {{x_{N-1}}, t} \right) - M\left( {{x_N}, t} \right) - \Delta x \cdot \rho /{D_0}}}{{{{\left( {\Delta x} \right)}^2}}} \end{array} $ | (8) |
因此,把(7)式和(8)式带入到(5)式(省略自由扩散项),可以得到:
| $ \frac{{{\rm{d}}M}}{{{\rm{d}}t}} = \left[{-{\rm{i}}\Omega + W} \right]M $ | (9) |
(9)式中,M是N阶向量,W是包含边界条件的拉普拉斯算符N×N矩阵,其表达式为:
| $ W = \frac{1}{{{{\left( {Vx} \right)}^2}}} = \left( {\begin{array}{*{20}{c}} {-\left( {1 + \frac{{Vx \cdot \rho }}{{{D_0}}}} \right)}&1&0&0& \cdot & \cdot & \cdot \\ 1&{-2}&1&0& \cdot & \cdot & \cdot \\ 0&1&{-2}&1&0& \cdot & \cdot \\ \cdot & \cdot & \cdot & \cdot & \cdot & \cdot & \cdot \\ \cdot & \cdot &0&1&{ - 2}&1&0\\ \cdot & \cdot & \cdot &0&1&{ - 2}&1\\ \cdot & \cdot & \cdot & \cdot &0&1&{ - \left( {1 + \frac{{Vx \cdot \rho }}{{{D_0}}}} \right)} \end{array}} \right) $ | (10) |
Ω是与磁场相关的矩阵,其计算公式为:
| $ {\Omega _{ij}} = \gamma {B_z}\left( {{x_j}} \right) * {\delta _{ij}} $ | (11) |
(9)式通过积分可以得到其一般表达式为:
| $ M\left( t \right) = \exp \left[{-{\rm{i}}\Omega + W} \right]M\left( 0 \right) $ | (12) |
其中,M(0)为磁化矢量的初始分布,设零时刻的磁化矢量在全空间均匀分布,即每个节点的磁化矢量相等,设为M(x, 0)=1/a.利用Crank-Nicholson方法可以将(12)式变为更稳定的数值求解形式:
| $ M\left( {t + \Delta t} \right) = {{\rm{e}}^{-{\rm{i}}\Omega \Delta t/2}}{\left( {1-W\Delta t/2} \right)^{-1}}\left( {1 + W\Delta t/2} \right){{\rm{e}}^{ - {\rm{i}}\Omega \Delta t/2}}M\left( t \right) = UM\left( t \right) $ | (13) |
因此各个时刻的磁化矢量就可以通过此数值求解过程得到.
2.2 随机游走方法(5)式也可以通过随机游走方法进行求解[15].该方法通过模拟大量粒子的布朗运动来实现,首先,随机游走的粒子随机的均匀分布在孔隙中,经过一个时间步长,粒子从初始位置运动到一个新位置点,这个新位置点处于以初始位置为球心、半径为s的球面上.时间步长Δt由下式给出:
| $ \Delta t = \frac{{{s^2}}}{{6{D_0}}} $ | (14) |
每一时间步长后的新位置点的计算公式如下:
| $ \begin{array}{l} x\left( {t + \Delta t} \right) = x\left( t \right)| + s\;\sin \phi \cos \theta \\ y\left( {t + \Delta t} \right) = y\left( t \right)| + s\;\sin \phi \sin \theta \\ z\left( {t + \Delta t} \right) = z\left( t \right)| + s\;\cos \phi \end{array} $ | (15) |
(15)式中角度θ是[0, 2π]随机产生的,
| $ \zeta = \frac{{2\rho S}}{{3{D_0}}} $ | (16) |
如果粒子存活下来,则在边界发生非弹性碰撞,其计算公式由模型的形状而定.这样,粒子各时刻的位置即可记录下来.
以上的方法为常规随机游走方法,为了使得粒子运动更加准确,半径s要求非常小,一般为几纳米,这样会导致模拟步骤增加,计算时间增长.Zheng和Chiew等人[16]通过定义一个累计密度函数,提出了第一旅行时间算法,其表达式为:
| $ \begin{array}{l} P\left( x \right) = 1 + 2\sum\limits_{n = 1}^\infty {{{\left( {- 1} \right)}^n}\exp \left[{-{{\left( {n\pi } \right)}^2}x} \right]} \\ x = \frac{{{D_0}\Delta t}}{{{r^2}}} \end{array} $ | (17) |
(17)式中0 < P(x) < 1,r表示初始位置到最近骨架的距离,如图 2所示,从位置0开始,半径为r1的最大球体决定了颗粒在非受限状态下可以运动的最大距离,给定一个随机的角度就可以确定粒子位移到达的位置,此次随机游走的时间步长通过累计概率密度曲线求取,首先,在[-1, 1]区间产生一个均匀分布的随机数赋予P(x),然后通过(17)式即可得到Δt.重复该过程,当颗粒落入距离骨架表面λ(一般取3s,为图 2中的外壳厚度)范围内时,采用常规随机游走算法进行计算.

|
| 图 2 第一旅行时间算法示意图 Fig. 2 Graphical illustration of principle of First-Passage-Time method |
岩石孔隙中的流体具有3种横向弛豫机制,分别为体弛豫T2B、表面弛豫T2S、扩散弛豫T2D,总的弛豫时间可以概括为下式:
| $ \frac{1}{{{T_2}}} = \frac{1}{{{T_{{\rm{2S}}}}}} + \frac{1}{{{T_{{\rm{2B}}}}}} + \frac{1}{{{T_{{\rm{2D}}}}}} $ | (18) |
Brownstein和Tarr[17]指出,在快扩散条件下(ρa/D0
| $ \frac{1}{{{T_{2s}}}} = \rho \frac{S}{V} $ | (19) |
S/V反映孔隙尺寸.例如,(1)单球形孔隙中,S/V=6/d,d为单球直径;(2)同一半径球形堆积为骨架的孔隙中,S/V=[6(1/φ-1)]/d.
梯度磁场中,由于分子的扩散引起磁化矢量额外的衰减,用扩散弛豫来表示.对CPMG脉冲序列,扩散弛豫表达式为:
| $ \frac{1}{{{T_{{\rm{2D}}}}}} = \frac{{{D_0}{{\left( {\gamma G{T_{\rm{E}}}} \right)}^2}}}{{12}} $ | (20) |
(20)式中,TE=2τ为回波间隔,τ为半回波间隔,G为磁场梯度值.为了模拟受限扩散对CPMG脉冲序列的影响,我们根据核磁共振测井中的实际情况设置模拟参数,根据斯伦贝谢CMR的参数,G=0.13 T/m,表面弛豫率ρ =10 μm/s,样品为蒸馏水T2B=3 s,TE=4 ms和0.2 ms进行比较.模型为板状模型,其磁场垂直于平行板延伸方向,板间距a分布为双峰模型,利用(19)式计算得到的T2S如图 3所示.

|
| 图 3 不同回波间隔下CPMG脉冲序列的自由扩散及受限扩散模拟对比结果.(a)TE=0.2 ms;(b)TE=4 ms Fig. 3 Comparison between theoretical calculations for free diffusion and simulation result for restricted diffusion with different echo spacing in slab. (a) TE=0.2 ms; (b) TE=4 ms |
磁化矢量计算步骤[18]简述如下:令半回波间隔τ=NΔt,即,把时间分成N个时间步长.对于CPMG脉冲序列,90°脉冲之后到第一个180°脉冲施加之前,其磁化矢量进动矩阵根据(13)式可以得到U+=UN.同样的,施加180°脉冲序列之后的进动矩阵为U-=U+T.因此,第一个回波幅度值为M(2τ)=U-U+M(0)=U2τM(0).第二个回波的计算为:M(4τ)=U+U-U-U+M(0)=U4τM(0).利用同样的方法可以计算第n个回波时的幅度值:
| $ M\left( {2n\tau } \right) = U_{2\tau }^{\mathit{\bmod} \left( {n, 2} \right)}U_{4\tau }^{\mathit{floor}\left( {n, 2} \right)}M\left( 0 \right) $ | (21) |
(21)式中,mod(n, 2)和floor(n, 2)分别表示n/2的余数及n/2的整数值.图 3为TE=0.2 ms和4 ms情况下的有限差分模拟结果.当TE=0.2 ms,扩散时间小,表观扩散系数与自由扩散系数相差不大,在模型中利用有限差分模拟得到的数据反演得到的总横向弛豫时间,与(18)式得到的自由扩散下的理论曲线几乎重合;当TE=4 ms,根据(18)式计算得到的点划线和模拟反演得到的圈线不再重合,这是因为扩散时间增大,表观扩散系数会小于自由扩散系数,(18)式中的D0将变小,而且孔隙越小,D(TE)越小,对应的圈线往右平移程度越大.
3.2 PFG(Pulsed Field Gradient)技术的模拟自从1963年发现了受限扩散现象,前人设计了很多技术来研究扩散效应,最重要的为PFG[19](脉冲梯度场),其脉冲序列如图 4所示.

|
| 图 4 脉冲梯度场脉冲序列示意图 Fig. 4 Graphical illustration of Pulsed-field Gradient |
图 4中,t1为脉冲梯度激发时间,g为脉冲梯度的大小,δ为脉冲梯度持续时间,Δ为分子的扩散时间.对自由扩散的流体而言,经过图 4所示的脉冲序列之后,磁化矢量的衰减大小为:
| $ M\left( {\delta, \Delta, g, \tau } \right) = \exp \left[{-\frac{{2\tau }}{{{T_2}}}-{D_0}{\gamma ^2}{g^2}{\delta ^2}\left( {\Delta-\frac{\delta }{3}} \right)} \right] $ | (22) |
当流体分子在受限几何形状中,(22)式不再成立.前人对简单几何形状(平行板状、单圆柱、单球形)中的理论利用各种数学方法进行求解,例如,高斯相近似方法(GPD),短脉冲梯度方法(SPG),长脉冲梯度方法(LPG).
由于圆柱和球形孔隙中边界条件用简单的矩阵不容易表达,而蒙特卡罗随机游走方法易于实现,因此可以利用随机游走进行数值模拟.由上述介绍可知,随机游走每一步步长和相应的时间步长都可以控制,对于脉冲梯度脉冲序列,其信号的采集计算可以通过下述方法实现.
如图 4所示,回波产生时刻第i个分子由于扩散造成的模拟相位变化为:
| $ {\phi _i} = \gamma g\left[{\int_{{t_1}}^{{t_1} + \delta } {{z_i}\left( t \right){\rm{d}}t}-\int_{{t_1} + \Delta }^{{t_1} + \Delta + \delta } {{z_i}\left( t \right){\rm{d}}t} } \right] \approx \gamma g\left[{\sum\limits_{j = a}^{a + b} {{z_{i, j}}}-\sum\limits_{j = a + c}^{a + b + c} {{z_{i, j}}} } \right]\left( {\Delta t} \right) $ | (23) |
(23)式中a, b, c分别表示t1,δ和Δ.得到所有粒子的相位以后,可以通过下式进行磁化矢量大小的计算:
| $ M\left( {\delta, \Delta, g, \tau } \right) \approx \frac{1}{N}\sum\limits_{i = 1}^N {\cos {\phi _i}} $ | (24) |
值得注意的是,(24)式中时间间隔对于常规随机游走是固定的,而对第一旅行时间算法是随步长的变化而变化的.粒子总数N一般要不 < 104.
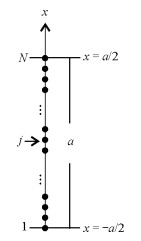
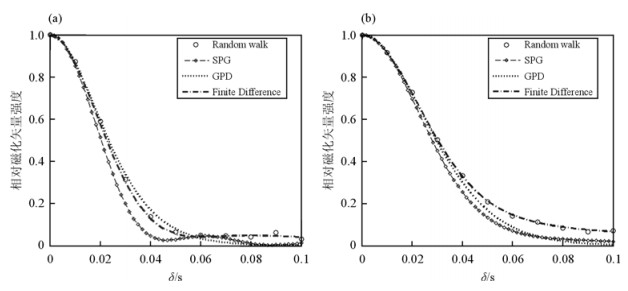
在板状模型中,与图 4所对应的回波的磁化矢量值与脉冲持续时间关系图如图 5所示.
|
| 图 5 脉冲梯度场板状模型模拟结果.(a)D0Δ/(a/2)2=1;(b)D0Δ/(a/2)2=0.2 Fig. 5 Simulation results of PFG pulse in slab. (a) D0Δ/(a/2)2=1;(b)D0Δ/(a/2)2=0.2 |
图 5(a)和(b)分别为两种板间距下的结果图,圈表示随机游走结果,较粗点划线表示利用有限差分得到的模拟结果,二者结果基本重合,表明了两种方法的可靠性,其他线条为GPD、SPG方法得到的理论曲线.模拟参数为(a):g=0.157 T/m和(b):g=0.009 8 T/m,磁场垂直板延伸方向.
利用随机游走方法对单球和单圆柱孔隙得到的模拟结果与理论结果对比图如下图 6所示.(a)表示单球形孔隙,(b)表示圆柱孔隙.模拟参数为(a):g=0.116 T/m,D0Δ/(R/2)2=0.2,R为球形半径长度,脉冲梯度施加方向为z轴方向;(b):g=0.116 T/m,D0Δ/(r/2)2=0.2,r为圆柱半径,脉冲梯度及磁场方向为垂直圆柱延伸方向的x轴方向.由于脉冲持续时间较短,因此,模拟结果与SPG理论结果基本一致.

|
| 图 6 脉冲梯度场模拟结果.(a)单球模型;(b)单圆柱模型 Fig. 6 Simulation results of PFG pulse in (a) single sphere and (b) single cylinder |
斯伦贝谢-道尔研究中心提出了二维扩散-弛豫核磁共振脉冲序列,如图 7所示,前面窗口进行扩散系数D的编辑,后面窗口是短回波间隔的CPMG脉冲.

|
| 图 7 扩散编辑脉冲序列示意图 Fig. 7 Graphical illustration of diffusion-editing pulse sequence |
建立与图 3相同的模型,同样是在板状模型中,利用有限差分进行模拟,把模拟得到的二维数据反演得到T2-D的分布图,如图 8所示.图中td表示分子扩散时间,等于Δ,由于回波间隔很小,故得到的T2分布表征孔隙尺寸的分布,T2越小,孔隙尺寸越小,同等的扩散时间下,流体分子受限的程度越大,表观扩散系数偏离自由扩散系数的距离越大.深色实线是扩散系数的对数平均值,反映了表观扩散系数的变化趋势.由于板状模型在磁场方向不连通,因此,表观扩散系数随着孔隙的减小而减小,表观扩散系数与自由扩散系数的比值甚至衰减一个数量级.核磁共振测井二维谱定义的自由流体水线在微小孔隙中不再准确,对岩石物理参数的求取产生一定的误差.

|
| 图 8 板状模型二维核磁共振模拟结果 Fig. 8 2D distribution for simulation in slab |
以上3个数值模拟结果都是基于板状、单球、单圆柱孔隙,而核磁共振测井研究的岩石是孔隙连通的介质,其运动特征更为复杂.因此,为了考察连通介质中的受限扩散现象,建立了球体堆积的两种模型.如图 9所示,半径为1的球堆积模型,(a)为周期堆积介质,孔隙是由半径大小相同的球按照一定规律排列形成的,此模型为1 000个球形成的孔隙空间,孔隙度为47.6%;(b)为随机堆积介质[20],孔隙是有大小相同的球随机堆积形成的,此模型球为1 149,孔隙度为39.9%.流体分子在其中均匀分布,然后利用随机游走算法对两种模型中的扩散进行模拟.为了观察流体分子在多孔介质中的运动趋势,不考虑表面弛豫,即分子的死亡概率为0.

|
| 图 9 孔隙介质模型.(a)周期球形堆积;(b)随机球形堆积 Fig. 9 The model for porous media. (a) periodic particle packing, (b) Random particle packing |
分子在多孔介质中的随机游走模拟结果如图 10所示,图中实线、虚线以及圈线分别为半径为60 μm、40 μm、20 μm下的结果.与闭合单孔隙介质中不同的是,连通介质中表观扩散系数与自由扩散系数的比值趋近于一个非零的常数,例如,图 10(a)中趋近于0.73;图 10(b)趋近于0.65.随着孔隙半径越小,其达到渐进值的时间越小.在20 μm情况下,其表观扩散系数在扩散时间为4 ms时,其值已经衰减为自由扩散系数的80%,因此,在扩散时间不变的情况下,随着孔隙的减小,表观扩散系数也随之减小.页岩气、煤层气等非常规油气资源所在的页岩孔隙有时空间尺寸达到几微米,甚至纳米级,此时分子的受限扩散不可忽略.

|
| 图 10 多孔介质中表观扩散系数随扩散时间的模拟结果图.(a)周期堆积模型;(b)随机堆积模型 Fig. 10 Simulation result of the apparent diffusion coefficient as a function of diffusion time in porous media |
通过有限差分和随机游走对分子在单孔隙及周期堆积、随机堆积模型多孔隙介质的数值模拟,得到以下结论.
(1)有限差分适用于板状模型这种简单模型,此方法快速、精确;常规随机游走对于随机堆积等复杂孔隙结构更方便,易于实现,弊端为需要大量粒子,计算时间较长,第一旅行时间算法的引入能够使得随机游走步长随粒子所在位置到孔壁骨架的距离相关,大大节省了时间.
(2)闭合孔隙和连通孔隙在微小孔隙中,分子表观扩散系数均会小于自由扩散系数,当孔隙尺寸 < 20 μm时,其受限扩散现象明显.
(3)无论在测井还是实验室条件下的核磁共振测量中,微小孔隙中的流体扩散系数均需重新考虑,因此利用二维核磁共振谱进行饱和度等岩石物理参数求取时,需要对这一现象予以校正.
| [1] | Coats G R, Xiao L Z, Prammer M G . NMR Logging Principles and Applications[M]. Houston: Gulf Professional Publishing, 1999 . |
| [2] | Li Xin(李新), Xiao Li-zhi(肖立志), Hu Hai-tao(胡海涛) . Characteristics of NMR logging while drilling tools(随钻核磁共振测井仪器探测特性研究)[J]. Chinese J Magn Reson(波谱学杂志) , 2011, 28 (1) : 76-83 |
| [3] | Song Y Q, Ryu S, Sen P N . Determining multiple length scales in rocks[J]. Nature , 2000, 406 (6 792) : 178-181 |
| [4] | Gong Guo-bo(龚国波), Sun Bo-qin(孙伯勤), Liu Mai-li(刘买利) et al . NMR relaxation of the fluid in rock porous media(岩石孔隙介质中流体的核磁共振弛豫)[J]. Chinese J Magn Reson(波谱学杂志) , 2006, 23 (3) : 379-395 |
| [5] | Freedman R, Heaton N, Flaum M, et al. Wettability, Saturation, and Viscosity from NMR measurements[C]. SPE Journal, 2003, 8(4): 317-327. |
| [6] | Hürlimann M D, Venkataramanan L . Quantitative measurement of two-dimensional distribution functions of diffusion and relaxation in grossly inhomogeneous fields[J]. J Magn Reson , 2002, 157 (1) : 31-42 DOI:10.1006/jmre.2002.2567 |
| [7] | Minh C C, Heaton N, Ramamoorthy R, et al. Planning and interpreting NMR fluid-characterization logs[C]. Society of Petroleum Engineers, 2003, SPE 84478. |
| [8] | Zielinski L J, Hürlimann M D . Probing short length scales with restricted diffusion in a static gradient using the CPMG sequence[J]. J Magn Reson , 2005, 172 (1) : 161-167 DOI:10.1016/j.jmr.2004.10.006 |
| [9] | Viswanathan K, Kausik R, Minh C C, et al. Characterization of Gas Dynamics in Kerogen Nanopores by NMR[C]. Society of Petroleum Engineers, 2011, SPE 147198. |
| [10] | Mitra P P, Sen P N . Effects of microgeometry and surface relaxation on NMR pulsed-field-gradient experiments: Simple pore geometries[J]. Phys Rev B , 1992, 45 (1) : 143 DOI:10.1103/PhysRevB.45.143 |
| [11] | Mitra P P, Sen P N, Schwartz L M et al . Diffusion propagator as a probe of the structure of porous media[J]. Phys Rev Lett , 1992, 68 (24) : 3555-3558 DOI:10.1103/PhysRevLett.68.3555 |
| [12] | Helmer K, Hurlimann M D, Deswiet T et al . Determination of ratio of surface area to pore volume from restricted diffusion in a constant field gradient[J]. J Magn Reson , 1995, 115 (2) : 257-259 DOI:10.1006/jmra.1995.1175 |
| [13] | Torrey H C . Bloch equations with diffusion terms[J]. Phys Rev , 1956, 104 (3) : 563-565 DOI:10.1103/PhysRev.104.563 |
| [14] | Blees M H . The effect of finite duration of gradient pulses on the pulsed-field-gradient NMR method for studying restricted diffusion[J]. J Magn Reson , 1994, 109 (2) : 203-209 DOI:10.1006/jmra.1994.1156 |
| [15] | Ramakrishnan T, Schwartz L, Fordham E et al. Forward models for nuclear magnetic resonance in carbonate rocks[C]. SPWLA 39th Annual Logging Symposium, 1998. |
| [16] | Zheng L H, Chiew Y C . Computer simulation of diffusion controlled reaction in dispersions of spherical sinks[J]. J Chem Phys , 1989, 90 (1) : 32-327 |
| [17] | Brownstein K R, Tarr C . Importance of classical diffusion in NMR studies of water in biological cells[J]. Phys Rev A , 1979, 19 (6) : 2446-2453 DOI:10.1103/PhysRevA.19.2446 |
| [18] | Sen P N, André A, Axelrod S . Spin echoes of nuclear magnetization diffusing in a constant magnetic field gradient and in a restricted geometry[J]. J Chem Phys , 1999, 111 : 6548-6555 DOI:10.1063/1.480009 |
| [19] | Stejskal E O, Tanner J . Spin diffusion measurements: Spin echoes in the presence of a time‐dependent field gradient[J]. J Chem Phys , 1965, 42 : 288-292 DOI:10.1063/1.1695690 |
| [20] | Valfouskaya A, Adler P, Thovert J F et al . Nuclear-magnetic-resonance diffusion simulations in porous media[J]. J Appl Phys , 2005, 97 (8) : 083510(01-12) |
 2014, Vol. 31
2014, Vol. 31



