Article Information
- 张晓东, 胡小平
- ZHANG Xiao-dong, HU Xiao-ping
- 基于多尺度计算方法的活体磁共振谱自动相位矫正和代谢物定量分析
- Peak-Specific Phase Correction for Automated Spectrum Processing of In Vivo Magnetic Resonance Spectroscopic Imaging Using a Multiscale Approach
- 波谱学杂志, 2014, 31(1): 32-39
- Chinese Journal of Magnetic Resonance, 2014, 31(1): 32-39
-
Article History
Received date: 2013-10-08
Revised date: 2013-11-18


2. Biomedical Imaging Technique Center, The Wallace H. Coulter Department of Biomedical Engineering, Emory University and Georgia Institute of Technology, Atlanta, GA 30322, USA
2. Biomedical Imaging Technique Center, The Wallace H. Coulter Department of Biomedical Engineering, Emory University and Georgia Institute of Technology, Atlanta, GA 30322, USA
In vivo proton magnetic resonance spectroscopic imaging (MRSI) or chemical shift imaging (CSI) is a non-invasive multi-voxel approach to detect the neurochemical distribution of the brain and has been widely used in preclinical and clinic studies[1-9]. Comprehensive data processing strategies have been developed for robust metabolite mapping of the human brain[10]. However, because of gradient induced eddy currents, local susceptibility variations and drift of the static field[11, 12], water suppression and lipid and macromolecule signals, in vivo MRSI of the brain is often associated with poor line shape and phase and baseline distortion. Reference signal based deconvolution is sometimes used to correct the phase errors arising from various instrument imperfections in order to obtain pure absorption spectra for quantification. While the reference scan approach is applicable in many situations, it prolongs the experimental time, particularly for multi-slice or whole brain studies. Furthermore, deconvolution with single reference peak only accounts for a zero-order phase error and is inadequate when high order phase corrections are needed. Many automated quantification approaches are developed for one-dimensional NMR spectra or single voxel MRS[13-17]. In addition, LC-model is a robust in vivo MRS processing package which uses a basis set for automatic metabolite quantification with single voxel or multi-voxel data analysis[18]. However, the popularity and application are limited in general MRS/MRSI users due to license cost.
Due to the complexity in quantifying cerebral metabolites with in vivo MRS, most approaches incorporate the use of prior knowledge in order to simplify the computational procedure and derive more reliable results. The prior knowledge can be obtained experimentally or empirically[13, 19, 20] to improve the spectral peak fitting for automatic quantification of brain metabolites. However, these approaches are not always robust and/or efficient when applied to multi-slice in vivo MRSI data because of large variations in the spectral line-shape, peak location, and baseline from voxel to voxel in different brain regions. As a result, the metabolite mapping can be biased by using a single piece of prior knowledge for fitting every spectrum in multi-slice MRSI. A multiscale approach for analyzing the in vivo MRSI has been explored previously[21]. In the multiscale approach, a pyramid representation of the original data is created by recursively averaging the voxels in each block from the bottom level to the top level. As a result, the spectra on the top of the pyramid have the best SNR (and poorest spatial resolution) due to voxel averages, while the ones at the bottom remain unchanged. The desired analysis is applied to the pyramid in a top-down fashion with the analysis at each scale guided by results at its previous scale as prior knowledge to define initial values of fitting parameters (such as peak frequency, line-width) and boundary constrains to simplify the optimization procedure of the curve fitting. This procedure is repeated until the bottom of the tree (i.e., the full resolution) is reached. Therefore, the prior knowledge of each voxel is estimated from the voxel itself and its neighbors. The multiscale approach has been demonstrated to be robust in the automatic analysis of MRSI in the human brain[21]. However, the need for phase correction in preprocessing may complicate the data analysis procedure in multi-slice or whole brain MRSI data analysis. In the present work, we implemented a robust and simple method for automatic quantification in multi-slice in vivo MRSI by incorporating the peak-specific phase-correction in the multiscale strategy.
1 Methods and materials 1.1 Data acquisitionTwo-slice in vivo proton MRSI data sets were acquired with a circular k-space coverage of 36-point diameter in normal volunteers (with proper consent and institutional approval) on a 1.5 T whole body Siemens scanner (Siemens Medical Systems, Iselin, NJ) with the standard Siemens quadrature head coil. The customer-built MRSI pulse sequence used an inversion recovery prepared spin echo sequence (TR/TE/TI: 2 000/135/170 ms, FOV=240 mm×240 mm, slice thickness=10 mm) with 3 CHESS pulses for water suppression. The data acquisition took approximately 40 min.
The original data matrix in each slice was 36×36×1 024. The data were zero-filling to 64×64×4096 during the preprocessing. Also, to simplify the whole data processing procedure, each spectrum was dividedinto the N-acetyl-aspartate (NAA) segment and the segment containing Choline (Cho) and Creatine (Cr). The phase correction and peak fitting of each segment were performed independently. In addition, in order to improve data processing efficiency, a brain mask was created to retain only voxels in the brain and eliminate the unwanted voxels in each slice for the processing.
1.2 Data ProcessingThe flowchart for the MRSI data analysis is illustrated in Fig. 1. All the data processing scripts were coded in MATLAB 5.2 (Mathworks, Inc., Boston, MA). The specific steps in the flowchart are described below.
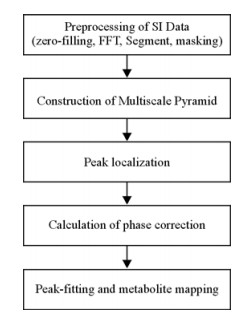
|
| Fig. 1 Flowchart of the data processing for multi-slice in vivo proton magnetic resonance spectroscopic imaging (MRSI) using the multiscale approach |
MRSI Reconstruction: The MRSI data of each slice were reconstructed in the spatial and temporal domains by using FFT after Zero-padding. A zero-padding factor of 2 was used in each dimension for the interpolation purpose. A Hanning window function was applied in the spatial reconstruction, and a Lorentzian window function (line Hz) was used in the time domain during the spectral reconstruction of MRSI. As Lorentzian function is the natural line shape of a single spin NMR signal, the Lorentzian window function applied in the time domain affects the linewidth of each metabolite peak in the frequency domain due to apodization effect. Therefore, the linewidth of Lorentzian window function is defined based upon the SNR of acquired MRSI data of Lorentzian window function with larger linewidth will improve the spectral SNR but reduce spectral resolution.
Metabolite Peak Identification and Subspectrum Extraction: A three-level multiscale approach was employed for searching the peak locations, starting from the largest scale (i.e. poorest spatial resolution) and moving to the finest scale (i.e. highest spatial resolution). In the specific case of the present study, the first (bottom) level was composed of the original 64×64 data matrix. The second level was a 32×32 data matrix reconstructed by averaging each block of 2×2 voxels in the first level. Similarly, the third (top) level was a 16×16 data matrix reconstructed by averaging each block of 2×2 voxels in the second level. The multiscale approach permits the frequency and linewidth of each metabolite peak at one scale as prior knowledge for identifying the same metabolite peak at the next (finer) scale. During the coarse-to-fine optimization procedure of spectral peak identification, the NAA peak is located first at each level since it usually has the best signal-to-noise ratio (SNR). As the frequency difference between the NAA, and Cho or peaks are fixed and known, the positions of Cho or Cr peak can be derived automatically after the NAA peak is identified. In the present study, the NAA segment and the segment containing Cho and Cr peaks were extracted from the original spectrum to simplify the spectral fitting and reduce the calculation time in multi-slice MRSI (Fig. 2).
Phase Correction: The phase correction was performed separately for each spectral segment. Although each spectrum is simplified due to the segmentation, its distorted baseline and phase varies from voxel to voxel, and not perfect in comparison with a standard absorption spectrum. Therefore, the contribution from both the real and imaginary parts is considered during the iterative optimization for automatic phase correction. The following function is minimized in the phase correction processing:
| $ S{\rm{ = abs}}\left[{\sum {\left( {{\rm{Imaginary}}\;{\rm{part}}} \right)} } \right] + {\rm{abs}}\left[{W/\sum {\left( {{\rm{Real}}\;{\rm{part}}} \right)} } \right] $ |
where W is an adjustable weighting factor to balance the contributions from the real and imaginary parts. W is adjusted empirically and its default value is estimated by equalizing contributions from the real (absorption) and imaginary (dispersion) parts which need to be maximized and minimized respectively. Subsequently, the real part of the spectrum was used for the spectral curve fitting in the next step.
Metabolite Map Generation: A Gaussian line shape with a linear baseline was fitted to each peak with the least-square fitting. The area under the Gaussian peak was then calculated to give the metabolite level of the corresponding metabolite in each segmented spectrum.
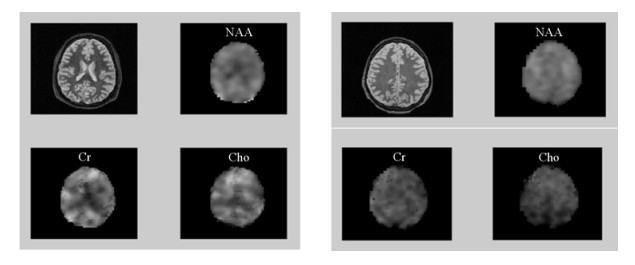
2 Results and DiscussionThe stacked spectra of a set of healthy human brain MRSI data with and without the multiscale-based phase correction are displayed in Fig. 2. In comparison with the original spectra, the corrected spectra demonstrate well improved line shapes in either the NAA sections or Cho and Cr sections [Fig. 2(b)]. The derived NAA, Cho, Cr metabolite maps for two-slice MRSI data set of the human brain are illustrated in Fig. 3.

|
| Fig. 2 (a) Uncorrected spectra from the in vivo proton MRSI data of a healthy human brain, (b) spectra with the phase distortion corrected using the multiscale approach in the same MRSI data set |
|
| Fig. 3 T2-weighted images and cerebral metabolite maps generated from the two-slice in vivo proton MRSI data of a healthy human brain with the phases corrected automatically using the multiscale approach |
As seen in the multiscale approach reported in the present study, the multiscale method is used to identify and localize the peaks of interest in each spectral segment and the peaks are then locally phase-corrected using an automatic algorithm proposed in the present study. Subsequently, the absorption spectra within these segments are curve-fitted to generate the corresponding metabolite map. By focusing on the metabolites of interest, each metabolite peak of interest can be isolated from the complex in vivo spectra containing signals from residual water, macromolecules, lipids, and other metabolites of no interest. Therefore, the phase correction procedure for each isolated peak is simplified substantially. Also as the reconstructed spectra at the coarsest scale have best SNR, the peak identification (frequency and linewidth parameters) can be estimated automatically at the coarsest scale and the resultant peak information can be passed onto the next level as prior knowledge, making the procedure fully automatic. Although only the most widely examined metabolites, NAA, Cho, and Cr, were quantified in the present work, our approach can be applied to quantification of other metabolites. Also, as the prior information is used for locating the peaks of interest, it may be applicable in EPI-related MRSI data acquisition[22, 23] which has the reduced SNR or large scale data processing for whole brain MRSI[8].
Prior knowledge has been used in several studies of in vivo MRS data analysis[18-20], demonstrating their effectiveness in in vivo metabolite quantification. In general, the prior information in these studies is normally fixed and will not change from voxel to voxel to incorporate the large variation in peak position, line shape, baseline of every voxel in human brain in vivo MRSI. In addition, most previous approaches focus on the distorted baseline removal with complicated algorithms. In contrast, the multiscale approach provides the prior information of metabolite peaks from the averaged spectra on the top level of the pyramid, and then optimized progressively from the coarse spatial resolution to the fine one. Therefore, the prior knowledge for the spectral fitting of each voxel is self-adaptive and more reliable. In comparison with other reported approaches of in vivo MRSI data analysis, the multiscale-derived metabolite maps are comparable but the calculation procedure is more simplified and robust and can be incorporated readily for various needs of spectral peak identification and spectrum curve fitting fitting of in vivo MRSI.
3 ConclusionIn summary, a robust algorithm has been presented for automatic phase correction in multi-slice in vivo proton MRSI. Results on in vivo MRSI data have demonstrated the effectivenvess and robustness in metabolite quantification of human brain MRSI studies. The approach may be used for data processing of multi-slice in vivo MRSI in preclinical and clinical studies.
| [1] | Podo F, Henriksen O, Bovee W M et al . Absolute metabolite quantification by in vivo NMR spectroscopy: I. Introduction, objectives and activities of a concerted action in biomedical research[J]. Magn Reson Imaging , 1998, 16 (9) : 1085-1092 DOI:10.1016/S0730-725X(98)00117-9 |
| [2] | Nelson S J, Vigneron D B, Star-Lack J et al . High spatial resolution and speed in MRSI[J]. NMR Biomed , 1997, 10 (8) : 411-422 DOI:10.1002/(ISSN)1099-1492 |
| [3] | Kurhanewicz J, Swanson M G, Wood P J et al . Magnetic resonance imaging and spectroscopic imaging: Improved patient selection and potential for metabolic intermediate endpoints in prostate cancer chemoprevention trials[J]. Urology , 2001, 57 (4 Suppl 1) : 124-128 |
| [4] | He Q, Xu R Z, Shkarin P et al . Magnetic resonance spectroscopic imaging of tumor metabolic markers for cancer diagnosis, metabolic phenotyping, and characterization of tumor microenvironment[J]. Dis Markers , 2003, 19 (2-3) : 69-94 |
| [5] | Golder W . Magnetic resonance spectroscopy in clinical oncology[J]. Onkologie , 2004, 27 (3) : 304-309 |
| [6] | Glunde K, Jiang L, Moestue S A et al . MRS and MRSI guidance in molecular medicine: targeting and monitoring of choline and glucose metabolism in cancer[J]. NMR Biomed , 2011, 24 (6) : 673-690 DOI:10.1002/nbm.1751 |
| [7] | Barker P B, Lin D D M . In vivo proton MR spectroscopy of the human brain[J]. Prog Nucl Mag Res Sp , 2006, 49 (2) : 99-128 DOI:10.1016/j.pnmrs.2006.06.002 |
| [8] | Stagg C J, Knight S, Talbot K et al . Whole-brain magnetic resonance spectroscopic imaging measures are related to disability in ALS[J]. Neurology , 2013, 80 (7) : 610-615 DOI:10.1212/WNL.0b013e318281ccec |
| [9] | Pan J W, Twieg D B, Hetherington H P . Quantitative spectroscopic imaging of the human brain[J]. Magn Reson Med , 1998, 40 (3) : 363-369 DOI:10.1002/(ISSN)1522-2594 |
| [10] | Maudsley A A, Darkazanli A, Alger J R et al . Comprehensive processing, display and analysis for in vivo MR spectroscopic imaging[J]. NMR Biomed , 2006, 19 (4) : 492-503 DOI:10.1002/(ISSN)1099-1492 |
| [11] | Spielman D M, Adalsteinsson E, Lim K O . Quantitative assessment of improved homogeneity using higher-order shims for spectroscopic imaging of the brain[J]. Magn Reson Med , 1998, 40 (3) : 376-382 DOI:10.1002/(ISSN)1522-2594 |
| [12] | Maudsley A A . Spectral lineshape determination by self-deconvolution[J]. J Magn Reson Ser B , 1995, 106 (1) : 47-57 DOI:10.1006/jmrb.1995.1007 |
| [13] | Alm E, Slagbrand T, Aberg K M et al . Automated annotation and quantification of metabolites in 1H NMR data of biological origin[J]. Anal Bioanal Chem , 2012, 403 (2) : 443-455 DOI:10.1007/s00216-012-5789-x |
| [14] | Song X, Zhang B L, Liu H M et al . IQMNMR: Open source software using time-domain NMR data for automated identification and quantification of metabolites in batches[J]. BMC Bioinformatics , 2011, 12 : 337 DOI:10.1186/1471-2105-12-337 |
| [15] | Kaartinen J, Mierisova S, Oja J M et al . Automated quantification of human brain metabolites by artificial neural network analysis from in vivo single-voxel 1H NMR spectra[J]. J Magn Reson , 1998, 134 (1) : 176-179 DOI:10.1006/jmre.1998.1477 |
| [16] | Hao J, Astle W, De Iorio M et al . BATMAN-an R package for the automated quantification of metabolites from nuclear magnetic resonance spectra using a Bayesian model[J]. Bioinformatics , 2012, 28 (15) : 2088-2090 DOI:10.1093/bioinformatics/bts308 |
| [17] | Osorio-Garcia M I, Sima D M, Nielsen F U et al . Quantification of in vivo 1H magnetic resonance spectroscopy signals with baseline and lineshape estimation[J]. Meas Sci Technol , 2011, 22 (11) : 114011-114020 DOI:10.1088/0957-0233/22/11/114011 |
| [18] | Provencher S W . Estimation of metabolite concentrations from localized in vivo proton NMR spectra[J]. Magn Reson Med , 1993, 30 (6) : 672-679 DOI:10.1002/(ISSN)1522-2594 |
| [19] | De Graaf A A, Bovee W M . Improved quantification of in vivo 1H NMR spectra by optimization of signal acquisition and processing and by incorporation of prior knowledge into the spectral fitting[J]. Magn Reson Med , 1990, 15 (2) : 305-319 DOI:10.1002/(ISSN)1522-2594 |
| [20] | Young K, Govindaraju V, Soher B J et al . Automated spectral analysis I: Formation of a priori information by spectral simulation[J]. Magn Reson Med , 1998, 40 (6) : 812-815 DOI:10.1002/(ISSN)1522-2594 |
| [21] | Zhang X, Heberlein K, Sarkar S et al . A multiscale approach for analyzing in vivo spectroscopic imaging data[J]. Magnet Reson Med , 2000, 43 (3) : 331-334 DOI:10.1002/(ISSN)1522-2594 |
| [22] | Metzger G, Sarkar S, Zhang X et al . A hybrid technique for spectroscopic imaging with reduced truncation artifact[J]. Magn Reson Imaging , 1999, 17 (3) : 435-443 DOI:10.1016/S0730-725X(98)00187-8 |
| [23] | Labadie C, Hetzer S, Schulz J et al . Center-out echo-planar spectroscopic imaging with correction of gradient-echo phase and time shifts[J]. Magn Reson Med , 2013, 70 (1) : 16-24 DOI:10.1002/mrm.v70.1 |
 2014, Vol. 31
2014, Vol. 31



