2. 浙江省疾病预防控制中心, 浙江 杭州 310051
2. The Center for Disease Control and Prevention of Zhejiang Province, Hangzhou 310051, China
流行性感冒(influenza)简称流感,是一种由流感病毒引起的急性发热性呼吸道传染病,临床表现为起病急、病程短、高热、头痛、乏力和全身酸痛等症状[1],主要通过空气飞沫或接触传播,具有很强的传染性,非常容易在人群中引起暴发或流行,甚至造成全球范围内的大流行,对社会的稳定和经济的发展产生严重威胁[2, 3]。浙江省位于中国东南沿海地区,近几年流感疫情时有发生。2009年全球甲型H1N1流感暴发,浙江省报告全年流感病例12 894例,死亡33例[4]。2010年底甲型H1N1流感再次袭来,死亡数人[5]。2011年中国卫生统计年鉴显示,浙江省甲型H1N1流感的发病率排在全国前五[6]。然而,流感发生频繁的浙江省目前仍缺乏适用于本省的流感预警技术,故探索适用且能应用于实际指导公众预防流感的流感预警技术是当前浙江省流感防控工作的迫切需求。
支持向量机(support vector machine,SVM)是一种基于统计学习理论的新型机器学习算法[7],它基于结构风险最小化原则,能够逼近复杂的非线性系统,具有较强的学习泛化能力,在解决分类和回归问题上表现出良好的性能。该方法所需样本数量少、建模方便、训练时间短、通用性较强。本研究通过收集近年来哨点医院门、急诊中的流感相关疾病病例资料,辅以气象条件、病原检测情况等数据资料,分析这些指标与流感样病例(influenza-like illness,ILI)发生的相关性,并尝试用SVM方法进行ILI预警,以期为流感疫情的早期发现提供有效的预测手段,尽可能降低流感带来的社会危害和经济损失。
1 资料与方法 1.1 流感和ILI相关疾病资料来源于浙江省国家级流感哨点医院的监测数据,每个地级市取1家哨点医院,共11家。时间跨度从2012年1月2日至2013年12月29日(即2012年第1周到2013年第52周),共计728天,104周。ILI的定义为发热(体温≥38 ℃)、同时伴有咳嗽或咽痛之一的急性呼吸道感染病例。收集同时期上述流感哨点医院内门急诊中流感相关疾病的初步诊断数据资料。科室范围包括内科门诊、内科急诊、发热门诊、儿内科门诊、儿内科急诊,其中内科门诊包括所有内科诊室和感染性疾病诊治科室。
1.2 气象资料气象资料来源于中国气象科学数据共享服务网站(http://cdc.nmic.cn/home.do),为同期浙江省24个国家气象台站的逐日气象资料,主要气象指标包括日降水量、日平均气压、日平均风速、日平均气温、日平均水汽压、日平均相对湿度、日最高气温、日最低气温等。
1.3 病原检测资料收集同期浙江省各个地级市疾病预防控制中心对哨点医院ILI采样的核酸检测结果和流感病原体的类型等。
1.4 数据预处理本研究是以周为时间尺度对流感的发生进行预警,故需对逐日收集的各项资料进行预处理,将其转换成以周为时间尺度的数据,方法如下:①将ILI每日报告数、门急诊中与流感相关的疾病病例数按周为单位进行合计;②计算日降水量、日平均气压、日平均风速、日平均气温、日平均水汽压、日平均相对湿度、日温差的周平均值;③取每周7 d内日最高气温的最大值为周最高气温,最低气温的最小值为周最低气温;④统计每周ILI样本中核酸检测结果为阳性的个数,并除以每周样本总数,得到周流感病毒检出阳性率。
1.5 ILI与其他因素的相关性分析将按周整理后的ILI例数与流感相关疾病患病数、各项气象因素、病原检出阳性率做相关性分析,筛选出与ILI发生有关的因素纳入预警模型。若资料满足二元正态分布,则采用Pearson积矩相关分析;若资料不满足二元正态分布,则采用Spearman秩相关分析。
1.6 建立ILI预警模型选取与ILI相关的因素,选用SVM中常用的ε-SVR算法和径向基(RBF)核函数,利用交叉验证选择最佳参数。利用前74周的数据建立ILI预警的SVM模型,并利用后30周的数据对模型进行验证。
1.7 统计学软件采用Excel 2010软件进行数据整理,SAS 9.2软件进行相关性分析,Matlab R2013a软件中的Libsvm软件包进行SVM模型的建立。检验水准α=0.05。
2 结 果 2.1 ILI报告病例基本情况104周内11家医院ILI报告病例数244 313人次。其中患者年龄在5岁以下的病例数为180 409人次,占57.59%;5岁及以上15岁以下的病例数为71 336人次,占22.77%;15岁及以上25岁以下的病例数为17 374人次,占5.55%;25岁及以上60岁以下的病例数为35 902人次,占11.46%;患者年龄在60岁及以上的病例数为8223人次,占2.63%。
2.2 ILI例数与其他因素的相关性分析考虑到发病前的潜伏期和疾病后效表现期,对ILI例数和流感相关疾病病例数、各类气象因素、病原检出阳性率做时滞相关性分析,相关系数见表1。根据相关性分析的结果,又考虑到对流感预警至少需要提前1周的数据,故最终选取以下8个相关因素:提前1周的流感相关疾病例数、病原检出阳性率;提前3周的周平均风速、周平均相对湿度;提前4周的周平均水汽压、周平均气温、周最低气温及周最高气温。
| 因 素 | 滞后0周 | 滞后1周 | 滞后2周 | 滞后3周 | 滞后4周 |
| 流感相关疾病例数 | 0.825** | 0.756** | 0.626** | 0.438** | 0.303** |
| 周平均气压 | -0.035 | 0.006 | 0.043 | 0.097 | 0.156 |
| 周平均风速 | -0.091 | -0.148 | -0.200* | -0.246* | -0.192 |
| 周平均气温 | -0.124 | -0.199* | -0.247* | -0.302** | -0.357** |
| 周平均水汽压 | -0.042 | -0.126 | -0.197* | -0.250* | -0.320** |
| 周平均相对湿度 | 0.007 | 0.122 | 0.132 | 0.220* | 0.198* |
| 周最低气温 | -0.101 | -0.165 | -0.212* | -0.260** | -0.313** |
| 周最高气温 | -0.076 | -0.145 | -0.162 | -0.240* | -0.288** |
| 周平均温差 | 0.060 | -0.077 | -0.081 | -0.097 | -0.132 |
| 病原检出阳性率 | 0.485** | 0.458** | 0.418** | 0.372** | 0.324** |
| *P<0.05;**P<0.01. | |||||
选择上述8个相关因素进行建模。为了避免在建模时因为数据之间数量级差别较大或量纲不同对模型的预测准确性产生影响,保证输出数据中数值较小的数据不会被吞食,提高收敛速度,缩短训练的时间,故在建模之前对数据进行归一化处理。
归一化公式为: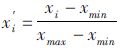
上式中,xi′为归一化后各因素的输入值;xi为归一化前各因素的输入值;xmax为各因素中的最大值;xmin为各因素中的最小值。
参数的选择:ε-SVR算法中的参数主要包括C、γ、ε,其中C为惩罚系数,γ为RBF核函数的宽度系数,ε为不敏感系数。研究采用交叉验证中的“留一法”,利用归一化后的前74周的数据来选择最佳参数。首先固定γ=0.1、ε=0.1,调整C值来观察拟合结果,见表2。从表2中可以看到,C值不同时模型的平方相关系数差别较大,而均方误差变化相对较小。当C<3时,平方相关系数不断增加;当C>3时,平方相关系数不断降低,故选取3为最佳C值。
| (γ=0.1,ε=0.1) | ||
| C值 | 均方误差 | 平方相关系数 |
| 0.001 | 0.0290 | 0.0289 |
| 0.01 | 0.0281 | 0.1359 |
| 0.1 | 0.0200 | 0.4227 |
| 1 | 0.0134 | 0.5421 |
| 2 | 0.0122 | 0.5788 |
| 3 | 0.0121 | 0.5804 |
| 4 | 0.0123 | 0.5708 |
| 5 | 0.0125 | 0.5662 |
| 10 | 0.0131 | 0.5459 |
| 100 | 0.0202 | 0.3816 |
固定C=3、γ=0.1,调整ε值来观察拟合结果,见表3。当ε<0.009时,平方相关系数不断增加;当ε>0.009时,平方相关系数不断降低;尤其是当ε≥1时,平方相关系数大幅度降低,故确定0.009为最佳ε值。
| (C=3,γ=0.1) | ||
| ε 值 | 均方误差 | 平方相关系数 |
| 0.0001 | 0.0115 | 0.6078 |
| 0.001 | 0.0114 | 0.6097 |
| 0.006 | 0.0113 | 0.6125 |
| 0.007 | 0.0112 | 0.6146 |
| 0.008 | 0.0111 | 0.6171 |
| 0.009 | 0.0111 | 0.6176 |
| 0.01 | 0.0111 | 0.6174 |
| 0.1 | 0.0121 | 0.5804 |
| 1 | 0.0357 | 0.0889 |
| 10 | 0.0357 | 0.0889 |
| 100 | 0.0357 | 0.0889 |
固定C=3、ε=0.009,调整γ值,结果见表4。当γ<0.4时,平方相关系数不断增加;当γ>0.4时,平方相关系数不断降低。故选取0.4为最佳γ值。
| (C=3,ε=0.009) | ||
| γ值 | 均方误差 | 平方相关系数 |
| 0.0001 | 0.0281 | 0.2244 |
| 0.001 | 0.0248 | 0.2701 |
| 0.01 | 0.0140 | 0.5212 |
| 0.1 | 0.0111 | 0.6176 |
| 0.2 | 0.0115 | 0.6039 |
| 0.3 | 0.0113 | 0.6135 |
| 0.4 | 0.0111 | 0.6198 |
| 0.5 | 0.0117 | 0.6015 |
| 1 | 0.0123 | 0.5901 |
| 10 | 0.0142 | 0.5067 |
| 100 | 0.0266 | 0.1180 |
经过上述分析,我们确定了模型的最优参数为:C=3,ε=0.009,γ=0.4,此时模型拟合的平方相关系数为0.6198,均方误差为0.0111。
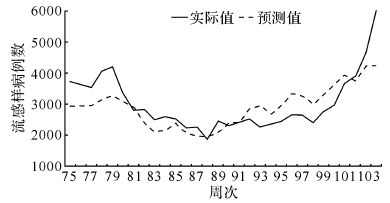
2.4 ILI预警模型的验证根据上述分析确定的最优参数,将前74周的数据纳入到模型中建立ILI预警模型。在对预警模型进行验证之前,我们先对ILI例数进行等级划分。根据常识,流感非流行时期在所有时期中占的比例较大,随着流行强度的增大,所出现的概率也越低。若简单地用ILI例数的四分位数来划分流感等级,则四个等级出现的概率相差不大,与实际不符;若用ILI例数的均值和标准差来划分,则会出现两头少、中间多的现象,与事实也不符合。根据经验,我们按照百分位P40、P70、P90来划分流感流行等级,将流感流行强度由弱到强的比例分为4︰3︰2︰1。将最后30周的数据代入两个预测模型中,得到最后30周的ILI例数的预测值(见表5)。结果显示:SVM模型预测流感等级与实际流感等级相符的有15周,同级预报正确率为50.0%;预测流感等级与实际流感等级相符或相差一级的有29周,预报正确率为96.7%。且预测值曲线与实际值曲线的总体趋势大体一致,但较实际值曲线平缓,峰谷不明显,见图1。
| 周次 | 实际ILI例数 | 预测ILI例数 | 实际流感等级 | 预测流感等级 |
| 75 | 3717 | 2926 | 3 | 2 |
| 76 | 3620 | 2954 | 3 | 2 |
| 77 | 3537 | 2927 | 3 | 2 |
| 78 | 4045 | 3131 | 3 | 2 |
| 79 | 4185 | 3265 | 4 | 2 |
| 80 | 3359 | 3112 | 3 | 2 |
| 81 | 2785 | 2881 | 2 | 2 |
| 82 | 2823 | 2405 | 2 | 1 |
| 83 | 2490 | 2097 | 1 | 1 |
| 84 | 2589 | 2126 | 1 | 1 |
| 85 | 2508 | 2377 | 1 | 1 |
| 86 | 2220 | 2038 | 1 | 1 |
| 87 | 2263 | 1978 | 1 | 1 |
| 88 | 1865 | 1949 | 1 | 1 |
| 89 | 2451 | 2062 | 1 | 1 |
| 90 | 2304 | 2383 | 1 | 1 |
| 91 | 2407 | 2397 | 1 | 1 |
| 92 | 2524 | 2838 | 1 | 2 |
| 93 | 2265 | 2972 | 1 | 2 |
| 94 | 2356 | 2661 | 1 | 2 |
| 95 | 2450 | 2934 | 1 | 2 |
| 96 | 2649 | 3330 | 1 | 2 |
| 97 | 2634 | 3285 | 1 | 2 |
| 98 | 2392 | 2961 | 1 | 2 |
| 99 | 2740 | 3297 | 2 | 2 |
| 100 | 2963 | 3610 | 2 | 3 |
| 101 | 3650 | 3923 | 3 | 3 |
| 102 | 3900 | 3733 | 3 | 3 |
| 103 | 4645 | 4205 | 4 | 4 |
| 104 | 6005 | 4245 | 4 | 4 |
|
| 图1 SVM模型的预测值与实际值比较 Fig.1 The comparison between predictive value and actual value |
SVM是一种基于统计学习理论的新型机器学习算法[7]。统计学习理论是目前针对小样本统计和预测学习的最佳理论和数学框架。在本研究中,我们共收集了两年共104周的数据,利用前74周数据训练模型,后30周数据验证模型,符合小样本的范畴,在这方面SVM方法是适用于本次研究的。其次,与小样本紧密联系的是高维问题。样本数的多少是相对的,在低维空间中小样本就可以描述整个样本空间;但是在高维空间,所需的样本数量会随着维数的增加而呈指数形式增长[8],进而产生维数灾难。SVM方法通过引入核函数有效解决了这一问题,使得操作可以直接在输入空间进行而不必到潜在的高维空间。因此,在使用SVM研究问题时不需要事先对高维数据进行降维,所以可以很方便地处理高维数据问题。在本研究中,我们利用医院门急诊中与流感相关疾病的病例数、各类气象因素以及病原检出阳性率来拟合ILI预警模型,而这些因素与ILI例数之间并非只是简单的线性相关,可能还存在复杂的非线性相关。SVM通过“核映射”,把输入样本空间映射到高维的特征空间,在特征空间中进行线性回归来实现非线性处理[9, 10]。因此,SVM也能很好地处理非线性问题,同样适用于本次研究。
SVM能充分利用样本的分布特征,在使用时不需过多的先验信息,根据一部分训练样本就可构建判别函数。而且其算法最终转化为二次寻优问题,理论上来说得到的是全局最优解。这样一来可以有效地避免其他机器学习算法(如神经网络等)易陷入的局部极值问题[11, 12]:SVM通过引入核函数和非线性变换巧妙地解决了高维问题,使其算法的复杂性与样本的维数无关;二来加快了训练学习的速度。另外,它还能根据有限的样本资料在模型的复杂性和学习能力之间寻求最佳折衷,保证了模型具有良好的泛化性能[13]。
此前没有适用于浙江省的ILI预警技术,对流感流行强度的等级划分也无特定的标准。本研究根据经验按照ILI例数的百分位数P40、P70、P90来划分流感流行等级,较平常简单地用ILI例数的四分位数或用ILI例数的均值和标准差来划分等级更符合实际情况。从本次研究的结果来看,SVM模型的同级预报正确率为50.0%,相差一级的预报正确率为96.7%,模型的正确率并不高,可能原因如下:①研究的时间序列是从2012年1月2日到2013年12月29日,而且是按周为单位来整理数据以及建模,时间序列不算长,无法考虑到季节等周期性较强的因素,对模型的拟合产生了一定的影响;②本次研究是针对全浙江省的研究,但是只收集了11家哨点医院的信息,医院样本数不够大,模型不够稳定,稍有偏差就会造成预测值与实际值相差很大,故预测结果不太理想;③本研究采用新方法对流感进行等级划分,而流感等级的划分对预测结果的准确性也有一定的影响,在等级划分这一问题上还需进行深入研究;④可能还存在其他的外界条件,如人员流动、空气污染等因素。我们没有将这些因素纳入模型,而这些因素恰恰也会影响流感的发生。在用SVM建模时,参数的选择也会影响到模型的拟合程度,故在参数选择方法上有必要作进一步研究。
| [1] | 李兰娟. 传染病学[M]. 北京: 高等教育出版社, 2004:13. LI Lan-juan. Epidemiology[M]. Beijing: Higher Education Press, 2014:13. (in Chinese) |
| [2] | VAN-DIJK A, ARAMINI J, EDGE G, et al. Real-time surveillance for respiratory disease outbreaks, ontario, Canada[J]. Emerg Infect Dis, 2009,15(5):799-801. |
| [3] | CHRETIEN J P, TOMICH N E, GAYDOS J C, et al. Real-time public health surveillance for emergency preparedness[J]. Am J Public Health, 2009,99(8):1360-1363. |
| [4] | 林君芬, 方 乐, 方琼珊, 等. 浙江省2009年甲型H1N1流感流行特征研究[J]. 浙江预防医学, 2010:22(9):5-7. LIN Jun-fen, FANG Le, FANG Qiong-shan, et al. Epidemiological characteristics of novel influenza A (N1H1) in Zhejiang Province in year 2009. Zhejiang Journal of Preventive Medicine, 2010:22(9):5-7. (in Chinese) |
| [5] | 侯 岩. 中国卫生年鉴.2010[M]. 北京: 人民卫生出版社, 2011: 45. HOU Yan. Year Book of Health in the People's Republic of China. 2010[M]. Beijing: People's Health Publishing House,2011:45. (in Chinese) |
| [6] | 中华人民共和国卫生部. 2011中国卫生统计年鉴[M]. 北京: 中国协和医科大学出版社, 2011: 266-273. Ministry of Health of the People's Republic of China. 2011 China Health Statistical Yearbook [M]. Beijing: Peking Union Medical College Press,2011:266-273. (in Chinese) |
| [7] | 张学工. 关于统计学习理论与支持向量机[J]. 自动化学报, 2000,26(1):36-46. ZHANG Xue-gong. Introduction to statistical learning theory and support vector machines[J]. Acta Automatica Sinica, 2000,26(1):36-46. (in Chinese) |
| [8] | 李应红, 尉询楷. 支持向量机和神经网络的融合发展[J]. 空军工程大学学报(自然科学版), 2005,6(4):74-77. LI Ying-hong, WEI Xun-kai. Fusion development of support vector machine and neural networks[J]. Journal of Air Force Engineering University(Natural Science Edition), 2005,6(4):74-77. (in Chinese) |
| [9] | 李 佳, 王 黎, 马光文, 等. LS-SVM在径流预测中的应用[J]. 中国农村水利水电, 2008,(5):12-14. LI Jia, WANG Li, MA Guang-wen, et al. Application of least squares support vector machines in runoff forecast[J]. China Rural Water and Hydropower, 2008,(5):12-14. (in Chinese) |
| [10] | GRITIANINI N, SHAW E-TAYLOR J. An introduction to support vector machines[M]. Cambridge: Cambridge University Press, 2000. |
| [11] | 姜万禄, 刘庆平, 刘 涛. 神经网络学习算法存在的问题及对策[J]. 机床与液压, 2003,(5):29-32. JIANG Wan-lu, LIU Qing-ping, LIU Tao. Drawbacks of neural network learning algorithms and countermeasures[J]. Machine Tool & Hydraulics, 2003,(5):29-32. (in Chinese) |
| [12] | 卢 敏, 张展羽. 径流预测的支持向量机应用研究[J]. 中国农村水利水电, 2006,(2):50-52. LU Min, ZHANG Zhan-yu. Application of support vector machine in runoff forecast[J]. China Rural Water and Hydropower, 2006,(2):50-52. (in Chinese) |
| [13] | 徐劲力. 支持向量机在水质评价中的应用[J]. 中国农村水利水电, 2007,(3):11-13. XU Jin-li. Application of support vector machine in water quality evaluation[J]. China Rural Water and Hydropower, 2007,(3):11-13. (in Chinese) |




