文章信息
- 刘晓默, 张梦琦, 林久祥
- LIU Xiaomo, ZHANG Mengqi, LIN Jiuxiang
- 正畸托槽与弓丝间摩擦力性能的实验研究
- Experimental Research on Friction between Domestic Brackets and Archwires
- 中国医科大学学报, 2019, 48(1): 23-28
- Journal of China Medical University, 2019, 48(1): 23-28
-
文章历史
- 收稿日期:2018-11-02
- 网络出版时间:2018-12-29 14:04
目前,轻力矫治的理念越来越受到正畸医生的关注。托槽与弓丝之间的摩擦力贯穿于整个正畸治疗的过程,研究显示临床上约50%~60%的正畸力要用来克服正畸过程中产生的摩擦力。减小摩擦力可以减轻患者的疼痛不适程度,降低牙根吸收和牙槽骨吸收潜在的风险,减少支抗丢失的可能性。正畸医生有必要了解正畸过程中摩擦力的影响因素,以便在临床治疗上有的放矢,对牙齿施以适当的正畸力,以获得牙齿及牙周等生物组织最佳反应及最佳矫治效果。
影响托槽和弓丝间摩擦力的因素很多,临界角是关键因素之一。临界角是牙齿发生倾斜至弓丝刚刚开始同时接触槽沟龈牙合两端时,托槽槽沟与弓丝之间的角度,是托槽与弓丝处于被动状态和主动状态交接点处的倾斜角度。当倾斜角未达到临界角时,摩擦力基本保持恒定,仅为经典摩擦力,大小不随倾斜角的变化而变化;当倾斜角达到临界角后(弓丝未达到刻痕状态之前),摩擦力包括经典摩擦力、约束摩擦力,大小随倾斜角的增加而呈线性增大。
本研究拟应用自主研发的正畸摩擦力测试仪[1],测试2种国产矫治器中的尖牙托槽与不锈钢弓丝呈不同倾斜角度情况下的摩擦力大小,探索不同托槽-弓丝组合的最大被动状态范围及临界角值。
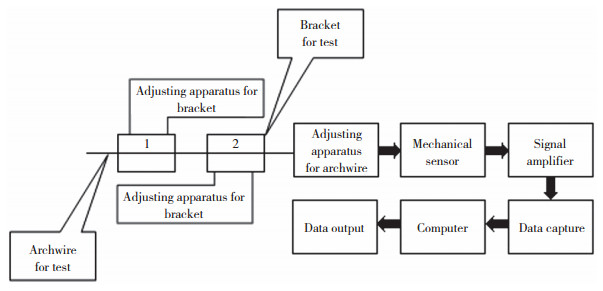
1 材料与方法 1.1 实验材料选用中国杭州新亚公司的MBT普通金属托槽和传动直丝弓标准托槽(第二代)为研究对象,2种托槽均为0.022”系统,均选取上颌尖牙托槽作为研究对象,采用美国TP公司的弹力结扎圈结扎,传动直丝弓标准托槽由于自身的“台阶”结构设计(图 1),采用全结扎和斜结扎2种弹力结扎方式。测试弓丝选用0.016”不锈钢圆丝和0.019”×0.025”不锈钢方丝(美国Plasdent公司)。摩擦力测试仪的工作原理如图 2所示。

|
| 图 1 传动直丝弓托槽的“台阶”结构 Fig.1 Step structure of transmission straight archwire bracket |
|
| 图 2 摩擦力测试仪工作原理图 Fig.2 Working principle of friction test instrument |
1.2 测试环境
每次实验测试前,更换新的弹力结扎圈并等待5 min,以消除结扎圈弹力释放不均对实验结果造成的影响;更换新的托槽和弓丝,以消除磨损对实验结果造成的影响;用95%乙醇棉球对托槽和弓丝进行脱脂处理,以消除各类附着物对实验结果造成的影响。
通过尖牙托槽调节装置中的手动角位台,调整尖牙托槽槽沟与弓丝之间的倾斜角θ,θ角的大小在弓丝滑动过程中保持不变。由于2种托槽临界角的理论计算值相差较大,实验测定的θ角设定为2种范围,MBT金属托槽θ角设为0°、0.5°、1°、1.5°、2°、2.5°、3°、4°、5°、6°、7°、8°;传动直丝弓标准托槽θ角设为0°、1°、2°、3°、4°、5°、6°、7°、8°、9°、10°、11°、12°、13°、14°、15°、16°、17°、18°、19°、20°、21°、22°、23°。分别测试不同θ角下,托槽与弓丝之间摩擦力的大小。实验在干态环境室温(23 ℃±2 ℃)下进行。
1.3 数据分析本研究除了测试出不同托槽-弓丝组合的摩擦力大小外,还需统计分析不同托槽-弓丝组合的临界角θc。采用二阶多项式回归法计算临界角(θc),该方法是本研究在分析既往研究的基础上探索出的新方法。首先,构造二阶多项式回归模型N = aθ2+bθ+c(a为二次项系数,b为一次项系数,c为常数),以托槽槽沟与弓丝间的倾斜角(θ)为自变量,测得的力值(N)为因变量,进行二阶多项式回归,得到第一个回归方程。根据理论分析可知,当θ < θc时(被动状态范围内),滑动摩擦力仅为经典摩擦力FR;当θ≥θc时(主动状态范围内),滑动摩擦力等于FR与约束力BI之和,即FR+BI[2-3]。因此,θ < θc时的摩擦力可近似地由θ=0时测得的摩擦力来表示,即FR=c(c为第一个回归方程中的常数项)。在实验的观测力值中扣除c(即FR)部分,得到的数值为BI。选择观测力值减去c后,仍稳定 > 0的部分进行一元线性回归,回归模型为N = aθ+b,仍以托槽槽沟与弓丝间的倾斜角(θ)为解释变量,测得的力值(N)为被解释变量,得到第二个回归方程,即为到达临界角后摩擦力值与倾斜角形成的方程。第二个回归方程的拟合线与N = c的交点对应的值就是临界角θc的数值,见图 3。

|
| 图 3 二阶多项式回归法的分析模式 Fig.3 Analysis paradigm of second-order polynomial regression |
2 结果 2.1 摩擦力
本研究对6组托槽-弓丝组合进行了不同倾斜角θ下的摩擦力测试,见图 4、表 1。各组数据均遵循同样的趋势,即首先摩擦力值保持平稳,随角度的增加变化不大,而在特定的角度(临界角)之后随角度的增加出现上升,并基本保持线性上升。各组托槽与弓丝间的摩擦力值不相同,临界角的大小也有所差异。

|
| 图 4 不同“托槽-弓丝”组合的摩擦力图 Fig.4 Friction force (gf) of combinations of brackets and archwire |
| Contact angel(°) | MBT & 0.016'' s.s. | MBT & 0.019''×0.025'' s.s. | TSA & 0.016'' s.s.(full ligation) | TSA & 0.019''×0.025'' s.s.(full ligation) | TSA & 0.016'' s.s.(oblique ligation) | TSA & 0.019'' ×0.025'' s.s.(oblique ligation) |
| 0 | 91.93±1.596 | 132.16±3.464 | 110.27±0.990 | 234.68±2.778 | 3.89±0.912 | 63.262±1.456 |
| 0.5 | 92.04±0.991 | 115.11±0.010 | - | - | - | - |
| 1 | 93.29±0.938 | 143.20±0.009 | 116.67±1.250 | 239.04±2.446 | 3.62±1.152 | 69.462±1.939 |
| 1.5 | 96.02±1.369 | 125.37±0.020 | - | - | - | - |
| 2 | 95.17±1.354 | 196.25±0.024 | 110.79±1.008 | 237.11±3.417 | 3.09±0.503 | 58.317±1.279 |
| 2.5 | 94.12±1.115 | 198.18±0.019 | - | - | - | - |
| 3 | 91.04±1.881 | 284.45±0.023 | 115.26±2.305 | 233.88±7.312 | 3.29±0.721 | 60.622±3.324 |
| 4 | 96.24±0.987 | 346.14±0.020 | 111.86±2.347 | 223.85±5.267 | 3.11±0.725 | 57.834±1.162 |
| 5 | 106.88±1.294 | 441.94±0.020 | 112.65±1.497 | 237.73±3.003 | 3.24±0.585 | 61.068±1.847 |
| 6 | 133.36±1.505 | 576.74±0.022 | 113.05±1.910 | 216.56±2.862 | 3.87±0.526 | 62.562±1.150 |
| 7 | 206.74±2.606 | 626.13±0.022 | 114.87±2.374 | 209.17±3.257 | 3.18±0.566 | 64.856±3.430 |
| 8 | 292.12±3.902 | 755.96±0.037 | 113.31±1.390 | 230.99±4.847 | 3.21±0.718 | 71.125±3.887 |
| 9 | - | - | 118.00±1.924 | 211.46±4.424 | 3.58±0.637 | 63.195±2.203 |
| 10 | - | - | 113.65±1.621 | 209.36±2.871 | 3.36±0.614 | 57.409±2.274 |
| 11 | - | - | 119.45±7.070 | 221.74±2.740 | 3.51±0.452 | 59.464±0.910 |
| 12 | - | - | 115.73±1.466 | 208.44±5.225 | 3.57±0.664 | 58.063±3.898 |
| 13 | - | - | 112.54±2.370 | 206.13±2.315 | 3.67±0.674 | 63.217±4.315 |
| 14 | - | - | 109.92±1.513 | 200.04±2.545 | 3.74±1.134 | 71.258±3.186 |
| 15 | - | - | 111.67±1.529 | 211.87±3.528 | 3.77±0.726 | 52.103±1.200 |
| 16 | - | - | 112.48±1.285 | 208.45±3.971 | 3.33±1.154 | 56.282±2.043 |
| 17 | - | - | 114.69±0.942 | 209.19±2.476 | 3.63±1.229 | 57.679±1.669 |
| 18 | - | - | 115.28±0.801 | 211.77±4.647 | 3.59±0.608 | 71.057±2.438 |
| 19 | - | - | 116.42±2.124 | 206.80±3.149 | 3.77±0.594 | 74.211±2.445 |
| 20 | - | - | 113.81±1.079 | 204.15±1.832 | 3.97±0.874 | 94.153±1.796 |
| 21 | - | - | 123.79±1.821 | 258.07±5.522 | 10.61±0.873 | 142.386±3.502 |
| 22 | - | - | 141.75±1.599 | 290.00±4.387 | 57.12±1.153 | 225.060±4.283 |
| 23 | - | - | 164.53±2.072 | 365.27±9.213 | 113.33±2.102 | 338.550±6.623 |
2.2 临界角
利用二阶多项式回归法,得出不同“托槽-弓丝”组合的回归方程和线性方程,并计算出临界角值θc,见表 2。
| Combination of brackets and archwire | Regression equation | Linear regression | Critical Contact angle(°) |
| MBT & 0.016'' s.s. | N=0.587θ2-0.94θ+90.847 | N=94.661θ-15.503 | 4.55 |
| MBT & 0.019''×0.025'' s.s. | N=118.535θ2-116.48θ+195.99 | N=94.661θ-15.503 | 2.23 |
| TSA & 0.016'' s.s.(full ligation) | N=9.509θ2-5.991θ+119.489 | N=20.372θ-304.833 | 20.83 |
| TSA & 0.019''×0.025'' s.s.(full ligation) | N=42.357θ2-30.997θ+233.184 | N=53.601θ-874.766 | 20.67 |
| TSA & 0.016'' s.s.(oblique ligation) | N=20.466θ2-13.295θ+6.11 | N=51.358θ-1 069.533 | 20.94 |
| TSA & 0.019''×0.025'' s.s.(oblique ligation) | N=55.082θ2-34.376θ+67.971 | N=52.521θ-919.115 | 18.79 |
3 讨论
在使用方托槽正畸治疗的过程中,牙齿不断发生着“倾斜-直立-倾斜-直立”的复杂变化[4],托槽槽沟表面及托槽翼内壁不可避免地要与弓丝相接触,互相间便随之产生了摩擦力。托槽与弓丝之间的摩擦力贯穿于整个正畸治疗的过程。
临界角(θc)的概念由KUSY等[2]于1997年提出,是牙齿发生倾斜至弓丝刚刚开始同时接触槽沟龈牙合两端时,托槽槽沟与弓丝之间的角度,是托槽与弓丝处于被动状态和主动状态交界点处的倾斜成角。正畸中的滑动摩擦力包括经典摩擦力、约束摩擦力和刻痕阻力3部分。托槽与弓丝间的摩擦力组成随两者相互状态的不同而变化:当托槽与弓丝之间的倾斜角小于临界角时,托槽与弓丝处于被动状态范围之内,滑动摩擦力仅为经典摩擦力,不随倾斜角的变化而变化;当倾斜角大于临界角时,托槽与弓丝处于主动状态范围之内,在弓丝没有到达刻痕状态之前[5],滑动摩擦力等于FR与BI之和(FR+BI),随倾斜角的增加呈线性增大[6];在弓丝到达了刻痕状态之后,滑动摩擦力等于FR、BI、刻痕阻力之和(FR+BI+NO)[2-3],这种情况不在正畸学研究范畴之内。
本研究结果提示,托槽与弓丝之间的摩擦力临界角大小与托槽的设计密切相关,传动直丝弓的尖牙托槽的临界角在18.79°~20.94°之间,MBT直丝弓托槽的临界角仅仅在2.23°~4.55°之间。可见传动直丝弓的尖牙托槽的临界角值显著大于MBT托槽。因此,传动直丝弓托槽在临床上允许尖牙发生更大范围的倾斜,利于牙齿移动,无论是对于不拔牙病例的牙齿排齐,还是对于拔牙病例的近远中向移动牙齿关闭间隙,都有积极的作用[7-9]。传动直丝弓矫治器及矫治技术,是林久祥教授经过10余年的研究与实践,探索研发出的具有自主知识产权的新一代低摩擦力直丝弓矫治器及矫治技术[10]。该矫治器的核心之处是尖牙托槽,吸纳了自锁托槽和Tip-Edge Plus托槽的优点。本研究显示传动直丝弓尖牙托槽具有如下特点:通过不同的结扎方式,与不同尺寸的弓丝组合,既能提供较小的摩擦力,又能提供较大的摩擦力。如图 2所示,传动直丝弓托槽与0.016''不锈钢圆丝斜结扎,其摩擦力值最小,几乎可以达到自锁托槽的效果[11-12];而传动直丝弓托槽与0.019''×0.025''不锈钢方丝全结扎时摩擦力较大,其被动范围内的摩擦力值最大。传动直丝弓托槽能够达到自锁托槽的“自锁”效果,主要是因为传动直丝弓托槽的设计者在近远中托槽翼之间增加了台阶(图 1),因此在对弓丝进行斜结扎时,该“台阶”结构使结扎圈(或结扎丝)与弓丝不接触或者少接触,大大减小了弓丝受到的结扎力,从而减少了托槽与弓丝之间的摩擦力。
该矫治器及矫治技术于2006年在第二届海峡两岸四地口腔正畸学术大会上公布,引起热烈反响,标志着我国正畸领域不是仅仅停留在引进、学习国外先进技术的水平,而是能够通过总结、比较、研究、实践进行自主创新,进入了一个新的阶段[13-15]。林久祥教授在研制矫治系统的同时,提出了“传动力及传动效应”的理论机制,在临床中实现轻力矫治,因此仅依靠简单的口内支抗基本满足临床需要。目前,第三代传动直丝弓矫治器正在研发之中,试图通过改进尖牙托槽的结构,进一步加大尖牙托槽的临界角[13]。本研究的结果将为传动直丝弓的临床应用及进一步研发提供实验依据。
临界角的实验值并非通过测试直接得出,而是依据测试出的摩擦力值,经过统计分析计算得来。不同的统计方法、不同的计算方法会导致临界角实验值不同。目前有关临界角体外实验的报道仅限于国外的KUSY等[16]和国内的LIU等[1]、丁鹏等[11],他们使用的都是理论临界值参考回归法,其方法是以临界角的理论计算值[6]作为被动范围和主动范围回归分析的分界点,分别求得回归方程后取交点,交点处的倾斜角即为临界角的实验值。这种统计方法相对简单,结论较为可靠。但是需要指出的是,理论临界值参考回归法预先设定了2个回归方程的范围,最终的回归结果在一定程度上依赖于理论临界角的数值,而非完全依据实验测量出的摩擦力观测值,因此,该统计方法仍存在一定的局限性。
本研究应用的二阶多项式回归法是首次提出并探索性应用于临界角计算的统计方法。这一大胆的尝试基于KUSY等[16]的研究,该研究发现二阶多项式的曲线能够很好地拟合各个倾斜角度下的实验观测值,但并未进一步应用二阶多项式计算临界角。本研究以这一发现为基础,尝试通过建立二阶多项式模型,计算临界角的数值,其优势在于数据的统计过程脱离了对理论值的依赖,完全依据实验测量出的摩擦力观测值。
在托槽相同的条件下,弓丝尺寸越大,临界角越小。在弓丝相同的条件下,托槽槽沟的设计对临界角大小的影响非常显著,如传动直丝弓托槽的临界角远大于MBT直丝弓托槽的临界角。
当托槽-弓丝之间倾斜角小于临界角时,摩擦力变化不大,不随倾斜角的变化而变化;当托槽—弓丝之间倾斜角大于临界角时,摩擦力随倾斜角的增大呈线性增加。
传动直丝弓托槽能够通过全结扎和斜结扎2种结扎方式,提供较大或较小的摩擦力,其独特的设计能够增大临界角,增加托槽与弓丝的被动范围,允许牙齿在移动过程中发生更大的倾斜。
| [1] |
LIU XM, DING P, LIN JX. Effects of bracket design on critical contact angle[J]. Angle Orthod, 2013, 83(5): 877-884. DOI:10.2319/080112-621.1 |
| [2] |
KUSY RP, WHITLEY JQ. Friction between different wire-bracket configurations and materials[J]. Semin Orthod, 1997, 3(3): 166-177. DOI:10.1016/S1073-8746(97)80067-9 |
| [3] |
KUSY RP, WHITLEY JQ. Influence of archwire and bracket dimensions on sliding mechanics:derivations and determinations of the critical contact angles for binding[J]. Eur J Orthod, 1999, 21(2): 199-208. DOI:10.1093/ejo/21.2.199 |
| [4] |
DRESCHER B, BOURANEL C, SCHUMACHER H. Frictional forces between bracket and archwire[J]. Am J Orthod Dentofac, 1989, 96(5): 397-404. DOI:10.1016/0889-5406(89)90324-7 |
| [5] |
KUSY RP. Ongoing innovations in biomechanics and materials for the new millennium[J]. Angle Orthod, 2000, 70(5): 366-376. DOI:10.1043/0003-3219(2000)070<0366:OⅡBAM>2.0.CO;2 |
| [6] |
THORSTENSON GA, KUSY RP. Resistance to sliding of self-ligating brackets versus conventional stainless steel twin brackets with second-order angulation in the dry and wet (saliva) states[J]. Am J Orthod Dentofac, 2001, 120(4): 361-370. DOI:10.1067/mod.2001.116090 |
| [7] |
封净, 范俊恒, 张佐, 等. 传动直丝弓技术矫治安氏Ⅱ类错颌临床疗效研究[J]. 宁夏医学杂志, 2017, 39(6): 556-557. DOI:10.16458/j.cnki.1007-0893.2017.05.064 |
| [8] |
赵伟. 传动直丝弓矫治器治疗安氏Ⅲ类错颌的临床研究[J]. 全科口腔医学电子杂志, 2018, 5(21): 40-41, 43. DOI:10.16269/j.cnki.cn11-9337/r.2018.21.023 |
| [9] |
王琦. 传动直丝弓矫治器在口腔正畸的临床应用效果分析[J]. 社区医学杂志, 2017, 15(21): 41-42. |
| [10] |
林久祥.牙齿矫正用传动矫治器[P].专利号: 200620108466.4. 2008-01-09.
|
| [11] |
丁鹏.两种自锁托槽拔牙矫治的临床研究及摩擦力实验研究[D].北京: 北京大学, 2007.
|
| [12] |
KAPUR R, SINHA PK, NANDA RS. Frictional resistance of the Damon SL bracket[J]. J Clin Orthod, 1998, 32(8): 485-489. |
| [13] |
林久祥. 矫正器及技术进展[J]. 中国实用口腔科杂志, 2009, 2(1): 5-8. DOI:10.3969/j.issn.1674-1595.2009.01.002 |
| [14] |
邹宏艺, 万志刚, 熊伟, 等. 传动直丝弓矫治器用于青少年牙齿矫正中的效果分析[J]. 中国继续医学教育, 2018, 10(24): 92-93. DOI:10.3969/j.issn.1674-9308.2018.24.049 |
| [15] |
杨永平, 刘广昌, 周沛玲. 传动直丝弓矫治器对青少年安氏Ⅱ类1分类错矫治的临床效果[J]. 深圳中西医结合杂志, 2017, 27(5): 131-132. DOI:10.16458/j.cnki.1007-0893.2017.05.064 |
| [16] |
KUSY RP, WHITLEY JQ. Assessment of second-order clearances between orthodontic archwires and bracket slots via the critical contact angle for binding[J]. Angle Orthod, 1999, 69(1): 71-80. DOI:10.1043/0003-3219(1999)069<0071:AOSOCB>2.3.CO;2 |
 2019, Vol. 48
2019, Vol. 48