0 引言

油气勘探风险分析实质上是对油气勘探成功率的预测，预测结果不仅可以为油气风险勘探目标优选提供科学依据，而且对提高油气勘探成效具有重要的实践意义和技术价值。因此近几十年来，许多国家的大型石油公司以及不同学者逐渐重视油气勘探风险预测问题，并围绕该问题开展广泛研究。2010年之前，油气勘探风险预测方法主要分为3类：基于不同地质条件的叠图法、信息融合法和基于随机过程及多元统计学的数据分析法。叠图法相对研究较早，其核心是将勘探要素(如烃源岩、储层、保存等)分为不同的图层进行叠加，从而凸显勘探风险信息，该类方法技术的优点是工作流程简单易懂且计算难度低^[1-2]。信息融合法改进了叠图法的缺点，基于多元统计理论，对多元地质数据进行处理，通过设计函数、分配权重、标准化等技术手段，实现对多元地质数据的降维，并进一步结合地理信息系统制图工具，实现地质风险的空间可视化^[3]。数据分析法着重体现对油气勘探风险概率在空间分布上的预测，其特点是利用已有探井、油气地质条件、储量区块分布等资料，从分析预测的角度表征油气资源在勘探工作中的空间分布特征; 该类典型方法包括马氏距离判别法^[4]、谱分解法^[5]、序贯高斯随机模拟法^[6]等。上述3类方法虽然取得了一定的效果，但是在应用过程中仍存在一些不足：(1)叠图法存在结果图中内容过于繁冗，且不同地质要素间主次关系不明确等缺点。(2)叠图法对专家经验依赖程度较强，其评价过程多以定性、半定性为主，且在分析过程中对探井约束的重视程度有所不足，因此评价结果主观程度较高，不同的专家对同一地区的预测结果可能存在较大的偏差。(3)信息融合法和数据分析法，在数据量较大时，存在数据挖掘不够，以及无法充分而有效地利用数据等缺点。2010年以来，为克服上述方法的不足，根据量化地质风险的不确定性，油气勘探风险评价中引入了三维马尔可夫链模型^[7]、地质模型的随机模拟^[8]和贝叶斯概率^[9-10]分析方法。综合应用经验，将地质、钻井、工程等不同领域的信息进行融合，量化表征地质风险，实现了地质风险概率预测模型的构建和勘探成功率预测^[11-15]。此外，贝叶斯网络作为不确定知识表示与推理的有效工具，近年来也被用来解决油气勘探问题，例如，基于贝叶斯网络编码油气系统在烃源岩层、储层和圈闭层面上的相关性，解决勘探远景分析问题^[16-18]; 基于贝叶斯网络整合地质因素预测油气空间分布^[19-20]。然而，上述文献中的贝叶斯网络方法只适用于某个特定的研究区，其通用性以及各个方法之间的优缺点和适用范围还有待进一步研究。

本文将贝叶斯网络技术引入到油气勘探风险预测中，分别构建了朴素贝叶斯分类器、树增强贝叶斯分类器、平均一阶依赖估计器和k阶依赖贝叶斯分类器4种油气勘探风险预测模型，总结了各种模型的优缺点及适用范围，并以准噶尔盆地腹部侏罗系三工河组203口探井及相关地质资料为数据基础，对各模型开展五折交叉验证。通过模型对比，优选出最优模型并对研究区油气勘探风险进行预测，预测结果可为该区未来油气勘探目标优选及探井部署提供定量的决策依据。

1 预测方法 1.1 石油地质问题转化概率预测模型

油气勘探风险预测，即油气资源空间分布预测，是根据地球科学资料、探井资料、盆地模拟资料并结合专家知识来定量预测潜在目的层的含油气空间变化规律。换句话说，就是在钻井之前有效地预测地下某个位置含有油气资源的概率。该地质问题可以转化为在多维地质因素空间中求解具有不确定性的二分类问题。假设某含油气区带中已经钻探m口探井，探井结果分为油气井和非油气井两类，相对应的区域为生产区和非生产区。实际勘探结果表明：(1)决定地下特定位置是否含有油气是多个地质因素共同作用的结果; (2)同一地质因素在生产区和非生产区具有不同的特征。因此分类的基本假设是，同一地质因素在不同组(类)间有显著差异，但在同一组(类)中没有显著差异。通过研究探井结果与影响油气发生的地质因素(假设有n个)之间的关系，可知地质因素$\boldsymbol{X}=\left\{X_1, X_2, \cdots, X_n\right\} $与探井结果C有如下映射关系：

$ f: \boldsymbol{X} \rightarrow C $

(1)

其中，C=0和C=1分别表示探井结果为非油气井和油气井。上述映射关系表明，多维地质因素X与探井结果C之间存在函数关系，即如果确定了X和C之间的函数关系，在钻井之前则可以利用未开发地区的多维地质信息计算地下含油气的概率，从而减少勘探风险及优化钻井策略。通过前人研究发现，这种计算可以用条件概率的形式表示。为了便于阅读和理解，本文约定大写字母(如X，Y)表示变量名称，小写字母(如x, y)表示对应变量的特定值，大写字母粗体(如X，Y)表示变量集合，小写字母粗体(如x, y)表示对应变量特定取值集合。假设已知某地下未勘探地点的地质信息为$ \boldsymbol{x}=\left\{x_1, x_2, \cdots, x_n\right\}$，则该位置的含油气后验概率可以表示为$P(C=1 \mid \boldsymbol{x}) $，根据贝叶斯定理可进行如下转化：

$ P(C=1 \mid \boldsymbol{x})=\frac{P(C=1, \boldsymbol{x})}{P(\boldsymbol{x})} $

(2)

为了减少计算公式(2)的复杂度，本文研究采用贝叶斯网络整合相关地质变量，进而计算油气的发生概率。

1.2 贝叶斯网络分类基本原理

贝叶斯网络是一种基于概率理论与图论进行大数据分析、推理和预测的数学模型。贝叶斯网络用来解决分类问题时称为贝叶斯网络分类器，其分类原理为：基于某一对象的先验概率，使用贝叶斯定理计算出其后验概率，然后使用最大后验(MAP)估计选出具有最大后验概率的类标签作为该事件的预测类标签^[21-22]。假设已知贝叶斯网络B，对于待分类的测试实例$ \boldsymbol{x}=\left\{x_1, x_2, \cdots, x_n\right\}$(n表示属性个数)，预测类标签c^*的MAP计算过程如下：

$ \begin{aligned} c^* & =\arg \max _{c \in \Omega_C} P_B(c \mid \boldsymbol{x})=\arg \max _{c \in \Omega_C} \frac{P_B(\boldsymbol{x}, c)}{P_B(\boldsymbol{x})} \\ & =\arg \max _{c \in \Omega_C} \frac{P_B(\boldsymbol{x}, c)}{\sum\limits_{c 1 \in \Omega_C} P_B(c 1, \boldsymbol{x})} \propto \arg \max _{c \in \Omega_C} P_B(c, \boldsymbol{x}) \\ & =\arg \max _{c \in \Omega_C} P_B(c) \prod\limits_{i=1}^n P_B\left(x_i \mid P a\left(x_i\right)\right) \end{aligned} $

(3)

其中，P_B表示根据贝叶斯网络B的概率分布。Ω_C表示变量C的所有可能取值的集合，即公式(3)中Ω_C={0, 1}。Pa(X_i)表示变量X_i的父节点集合，Pa(x_i)表示Pa(X_i)的具体取值，即$ P a\left(x_i\right) \in \Omega_{P a\left(X_i\right)}$。

1.3 贝叶斯网络分类器基本模型

本文主要介绍4种不同的贝叶斯网络分类器，分别为朴素贝叶斯分类器(NB)、树增强贝叶斯分类器(TAN)^[23]、k阶依赖贝叶斯分类器(KDB)^[24]和平均一阶依赖估计器(AODE)^[25]。NB是最简单的贝叶斯网络分类器，它假设给定类标签C时属性彼此独立，即

$ P_B(\boldsymbol{x} \mid c)=\prod\limits_{i=1}^n P_B\left(x_i \mid c\right) $

(4)

由于NB具有有效性和简洁性的特点，已广泛应用于分类学习。NB分类决策公式如下：

$c^*=\arg \max\limits _{c \in \Omega_C} P_B(c) \prod\limits_{i=1}^n P_B\left(x_i \mid c\right) $

(5)

TAN放松了NB中属性之间独立性的假设，将NB从零阶依赖扩展到一阶依赖，即$ \left|P \mathrm{a}\left(X_i\right)\right| \leqslant 2$。TAN使用条件互信息$ C M I\left(X_i ; X_j \mid C\right)$度量任意不相等的属性对X_i和X_j的依赖程度，CMI定义如下：

$C M I\left(X_i ; X_j \mid C\right)=\sum\limits_{x_i, x_j, c} P\left(x_i, x_j \mid c\right) \log _2 \frac{P\left(x_i, x_j \mid c\right)}{P\left(x_i \mid c\right) P\left(x_j \mid c\right)} $

(6)

一般情况下，TAN比NB具有更好的分类性能，通常被认为是最佳的单依赖分类器。TAN分类决策公式如下：

$ c^*=\arg \max \limits_{c \in \Omega_C} P_B(c) P_B\left(x_r \mid c\right) \prod\limits_{i=1, i \neq r}^n P_B\left(x_i \mid c, x_{j(i)}\right) $

(7)

其中，x_r代表根节点X_r的具体取值，X_j(i)表示X_i父节点集Pa(X_i)中除了C以外的节点，x_j(i)为X_j(i)的具体取值。

KDB允许每个属性节点最多有k个父节点。在构造KDB结构的过程中，首先对属性排序，即根据属性变量X_i与类变量C之间的互信息值对所有属性进行降序排列。然后为每个属性节点找到k个父节点。假设当前待选节点为X_i，依次为其找到k个具有最大$C M I\left(X_i ; X_j \mid C\right)$值的属性X_j作为父节点，且$X_j \in\left\{X_1, X_2, \cdots, X_{i-1}\right\}$。KDB分类决策公式如下：

$ c^*=\arg \max \limits_{c \in \Omega_C} P_B(c) \prod\limits_{i=1}^n P_B\left(x_i \mid c, x_{i 1}, \cdots, x_{i p}\right) $

(8)

其中，$\left\{x_{i 1}, \cdots, x_{i p}\right\}$是变量X_i的父变量集中除了C以外的节点的具体取值，$p=\min (i-1, k) $。

AODE基于集成的思想来提高NB的分类性能。在AODE模型构建过程中，依次选择属性节点X_i作为超父节点，并使用类变量C作为其他属性的共同父节点来构建子分类器，即子分类器的数量等于属性节点的数量。最后，所有子分类器结果的平均值就是AODE的分类结果。AODE分类决策公式如下：

$ c^*=\arg \max \limits_{c \in \Omega_C} \frac{1}{n} \sum\limits_{1 \leqslant i \leqslant n}\left(P_B\left(c, x_i\right) \prod\limits_{j=1, j \neq i}^n P_B\left(x_j \mid c, x_i\right)\right) $

(9)

假设C表示探井类别，$ \boldsymbol{X}=\left\{X_1, X_2, \cdots, X_n\right\}$表示n个与油气相关的地质因素，$\boldsymbol{x}=\left\{x_1, x_2, \cdots, x_n\right\} $表示某个待计算位置的地质信息(在本文中，节点、变量和地质因素的含义是等价的，他们分别对应图模型、概率论及石油地质上的概念，即属性节点、属性变量和地质属性表示相同的含义)。本文以AODE模型为例说明基于贝叶斯分类器的油气空间分布模型构建与预测过程，主要步骤如下：

(1) 如图 1所示，依次选择每个地质属性作为其他属性的超父节点，建立n个子分类器的拓扑结构(AODE_s1, AODE_s2, …, AODE_sn)。

(2) 根据每一个拓扑结构AODE_si计算其条件概率分布θ_si，得到n个子分类器(AODE₁, AODE₂, …, AODE_n)。

(3) 对于每一个类标签$c_p(p=0,1) $重复以下步骤：

① 对于每一个AODE_o$(o=1,2, \cdots, n) $，使用AODE_o计算x属于c_p的概率$P\left(c_p \mid \boldsymbol{x}\right)_o $。

② 平均所有概率$P\left(c_p \mid \boldsymbol{x}\right)=\frac{1}{n} \sum\limits_{o=1}^n P\left(c_p \mid \boldsymbol{x}\right)_o $。

(4) 返回所有类标签概率$P\left(c_o \mid \boldsymbol{x}\right), P\left(c_1 \mid \boldsymbol{x}\right) $。

1.4 4种不同贝叶斯网络分类器的优缺点及适用范围

通过对各个方法进行深入分析研究，表 1总结了4种不同贝叶斯网络分类器的优缺点及适用范围。

2 应用实例 2.1 研究区地质背景

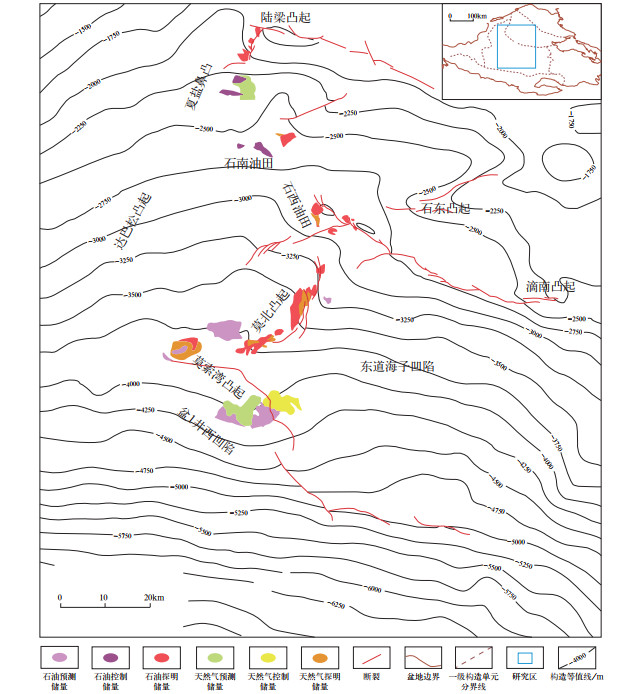
研究区位于准噶尔盆地腹部(图 2)，东西宽160km，南北长170km，面积约为2.7×10⁴km²，包括盆1井西凹陷、莫索湾凸起和石东凸起等^[26]。目的层为侏罗系三工河组(J₁s)，烃源岩为二叠系下乌尔禾组(P₂w)，盖层为侏罗系内部泥岩(图 3)。研究区南低北高，岩相南细北粗，油气自下而上、由南向北运移，形成断鼻型、断块型和岩性地层型等油气藏。截至2019年底，钻遇三工河组并完成试油的探井和评价井为203口，已发现三级石油、天然气地质储量分别为1.128×10⁸t和459×10⁸m³，主要分布在莫索湾凸起、莫北凸起、石西油田、石南油田和夏盐鼻凸(图 2)。

2.2 地质条件定量评价

从供烃条件(油气来源与充注条件)、储层条件、圈闭条件、盖层与保存条件四大方面定量评价油气成藏地质条件，成藏地质条件评价值高的地区油气资源分布概率高。

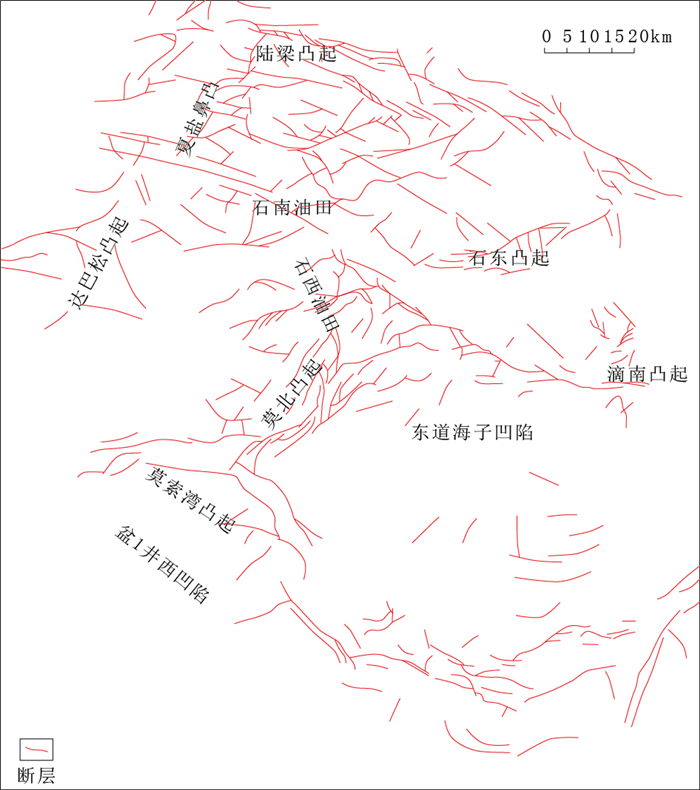
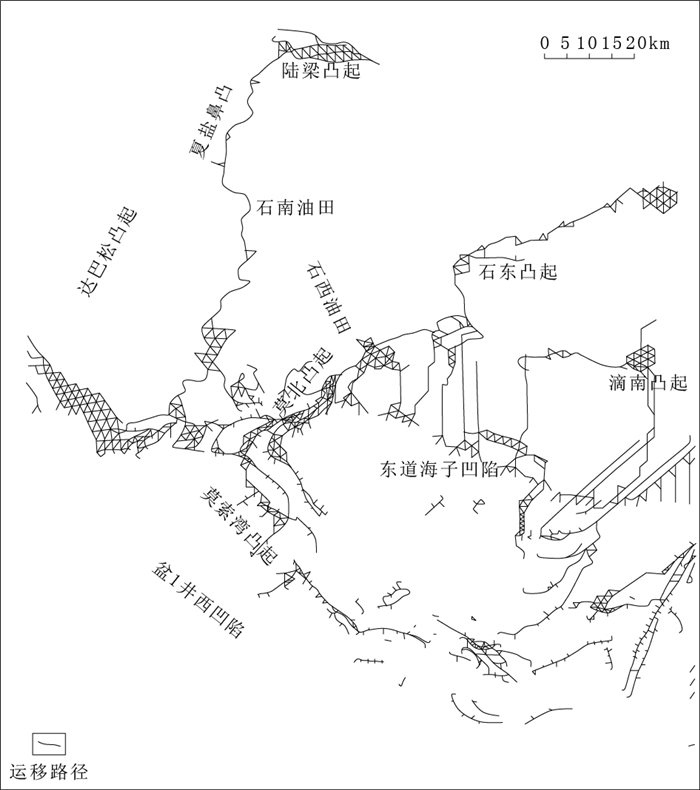
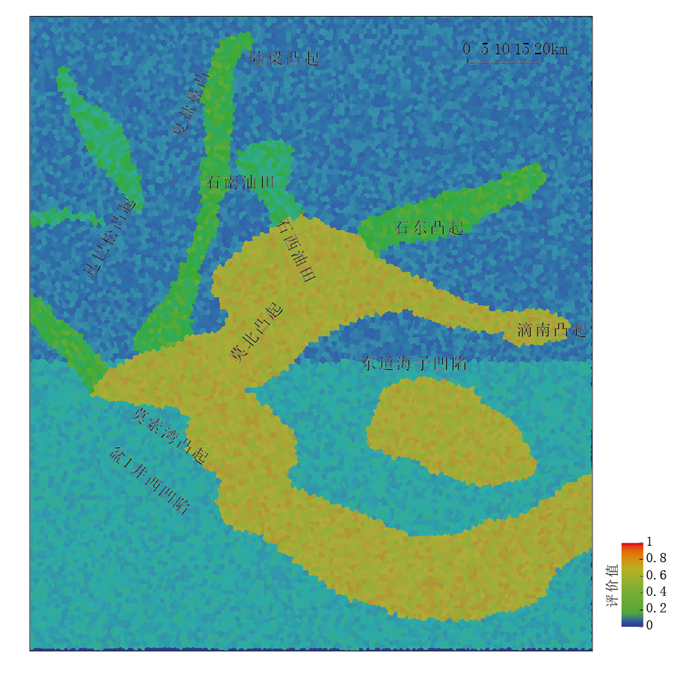
2.2.1 供烃条件

研究区三工河组油气主要来自下伏二叠系下乌尔禾组烃源岩，垂向上主要通过烃源断裂沟通，侧向运移主要受砂体和构造脊控制。研究区南部离油源较近，断层起到重要沟通作用，供烃条件整体相对有利; 北部离油源远，多达上百千米，断层不能沟通烃源岩，主要依靠长距离侧向运移提供油气，供烃条件整体相对不利。基于以上认识，在完成断裂分布研究和油气运移路径模拟的基础上(图 4、图 5)，将供烃条件划分为5个等级，即：沟通油源断裂+主路径、主路径、次要路径、南部近源区和北部远源区(表 2)。同样，采用随机抽样方法，绘制出供烃条件定量评价图(图 6)。

2.2.2 储层条件

根据研究区38个三工河组油藏评价数据，可知油藏储层平均有效厚度为8.6m，平均有效孔隙度为13.87%，平均含油饱和度为58.7%，平均原油密度为0.857t/m³(表 3);通过分析研究区16个三工河组天然气藏评价数据，可知气藏储层平均有效厚度为7.6m，平均有效孔隙度为12.64%，平均含气饱和度为60.4%，平均体积换算系数为285.7(表 3)。总体看，研究区储层有效厚度较薄、有效孔隙度较大，属于常规储层。

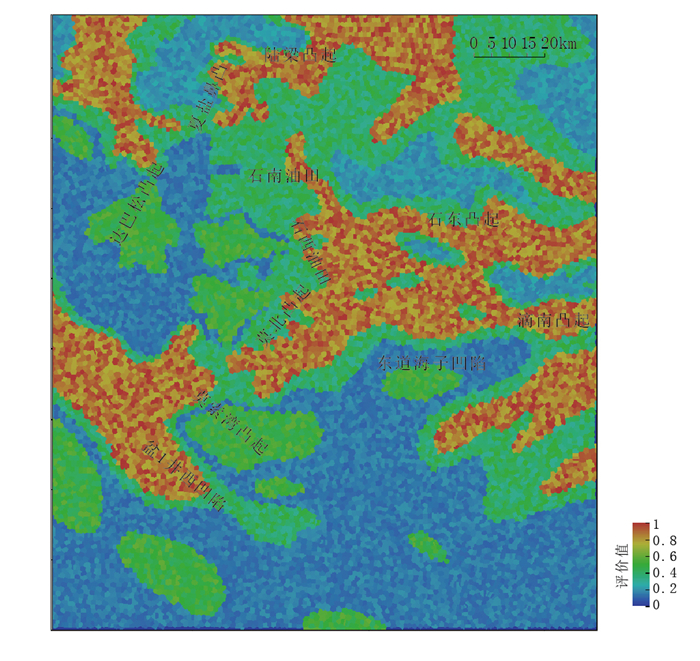
沉积相图(图 7)揭示，研究区主要发育水下分流河道、分流间湾、砂质碎屑流、席状砂、滩坝等三角洲相和滨浅湖相。由统计分析可知：位于水下分流河道和席状砂的井中，油气井占66.2%;位于滩坝、砂质碎屑流和分流间湾的井中，油气井占37.8%;位于滨浅湖的井中，油气井占21.2%。以沉积相为基础，以统计数据为依据，结合38个油藏和16个气藏的物性数据(表 3)，对储层条件进行定量评价，按优劣顺序依次为：水下分流河道、席状砂、滩坝及砂质碎屑流、分流间湾和滨浅湖，相应的评价值见表 4。在同一个沉积相中，每一个点的评价值为所属沉积相最小值到最大值之间的随机抽样结果。以水下分流河道为例，抽样范围为0.7到0.9，随机抽样结果为0.7到0.9之间的任意实数，包括0.7和0.9。根据以上方法，将沉积相图转化为储层条件定量评价图(图 8)，实现储层定量评价。

2.2.3 圈闭条件

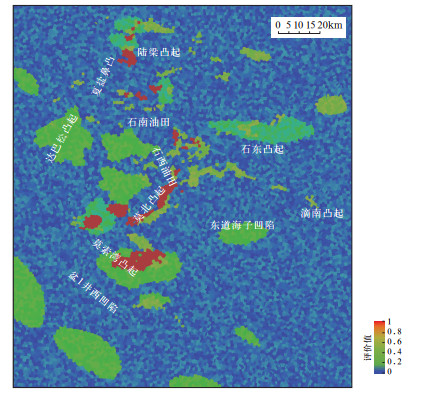
根据研究区三工河组顶界构造图及圈闭解释成果资料，将构造型圈闭划分为落实圈闭和待落实圈闭两级(表 5)。根据沉积相图将岩性圈闭划分为岩性透镜体(滩坝等)圈闭和岩性遮挡(分流间湾等)圈闭两级。另外，已发现油气藏为确定性圈闭。同样采用随机抽样方法，绘制出圈闭条件定量评价图(图 9)。

2.2.4 盖层与保存条件

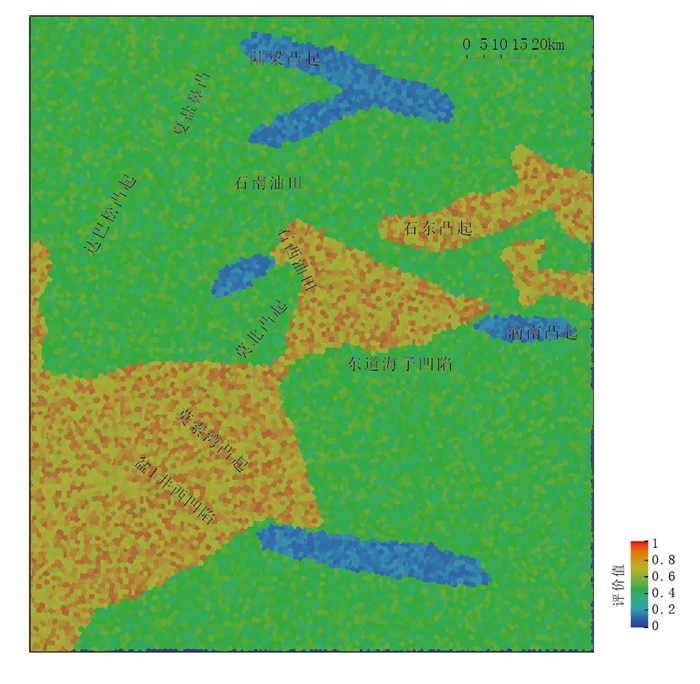
盖层与保存条件主要考虑上覆地层断裂发育情况和不整合风化带分布。上覆地层断裂起到破坏作用，评价值较低，取0.1~0.2;不整合风化带起到较好的遮挡作用，评价值较高，取0.7~0.9;其他区域泥岩相对发育，具备局部盖层作用，评价值取0.4~0.6。同样，通过随机抽样的方法获得盖层与保存条件定量评价图(图 10)。

2.3 训练集地质参数构建 2.3.1 油气井与非油气井分布

研究区钻遇三工河组试油井203口，其中油气井109口，非油气井94口(图 11)。将这203口井作为贝叶斯网络分类器的训练集。

2.3.2 数据集

依次采集研究区三工河组供烃条件定量评价值(图 6)、储层条件定量评价值(图 8)、圈闭条件定量评价值(图 9)、盖层与保存条件定量评价值(图 10)，得到203口井的地质参数表(表 6)，即三工河组探井数据集。

2.4 五折交叉验证与方法选择 2.4.1 数据分组

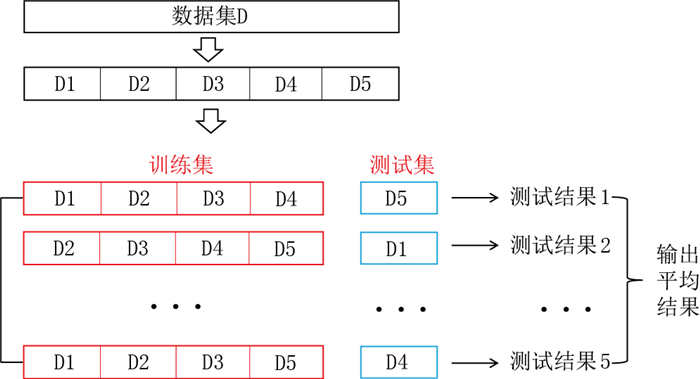
本文采用五折交叉验证方法测试4种贝叶斯网络的分类表现。图 12展示了五折交叉验证原理示意图。具体而言，首先将203口探井数据集随机近似等分成5组，其中4组作为训练集，剩余的1组作为测试集; 然后通过5次不同的组合形成5套训练集和测试集; 最后将5次测试结果的平均值作为评估方法的最终输出值。表 7详细地描绘了不同的分组情况及对应的实验结果。

2.4.2 结果分析

从表 7可知，NB、TAN、AODE和KDB在训练集上判别正确率分别为85.71%、86.70%、87.32%和88.92%，均大于85%，说明训练集参数分类有效; 测试集判别正确率分别为82.76%、83.25%、85.22%和82.76%，均大于82%，说明预测成功率高。

2.4.3 方法选择

从训练集准确度结果来看，KDB和AODE高于TAN和NB，表明KDB和AODE对数据的拟合程度更好; 但是从测试集准确度来看，AODE和TAN高于KDB和NB，说明AODE和TAN的泛化能力(预测能力)更好。综合来看，KDB过拟合数据，NB欠拟合数据，而AODE无论是对数据的拟合还是泛化能力均好于TAN，因此选择AODE作为研究区油气勘探风险预测方法。

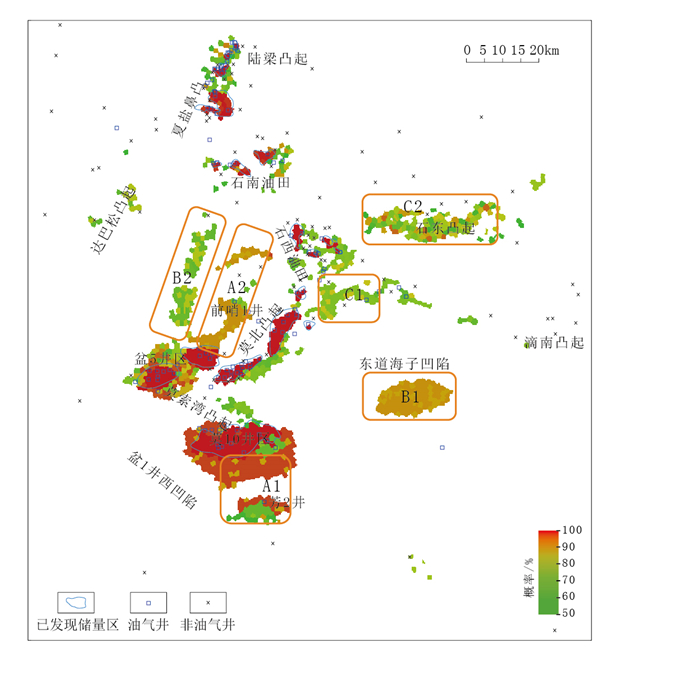
2.5 油气勘探风险预测结果及有利区优选

本文采用二维PEBI(Perpendicular Bisection)网格技术构建了15951个评价单元。利用研究区203口井组建的训练集进行AODE模型训练，然后采用AODE模型对所有评价单元进行含油气概率预测，并绘制出含油气概率分布图(图 13)，概率大于50%的单元为可能的含油气单元。

从图 13中可以发现，已发现储量区(三级储量)预测的油气概率最大，说明预测结果与勘探结果吻合度高。在储量区外，预测出一些油气概率大于50%的区域，主要包括3类不同类型的有利区：

(1) A类有利区。A类有利区位于储量区周边。根据预测结果优选两块(图 13)：①莫索湾凸起东南侧(A1)，包括芳2井附近; ②莫北凸起西北侧(A2)，包括前哨1井附近。

(2) B类有利区。B类有利区目前暂时还未布置探井，根据预测结果优选两块(图 13)：①东道海子凹陷附近(B1);②莫北凸起与达巴松凸起之间(B2)。

(3) C类有利区。C类有利区属于复杂区，已有一些钻探和发现，但未能提交储量。根据预测结果优选两块(图 13)：①莫北凸起东北侧(C1);②石东凸起附近(C2)。

A类有利区，把握程度较高，是下一步油田扩边和滚动勘探的重点区; B类有利区，不确定性相对较高，是下一步风险勘探和甩开勘探的重点区; C类有利区，地质条件复杂，需要进一步开展研究，取得新认识后，才能制定钻探部署，提交储量。

3 结论

地质风险预测既是基于多维地质因素空间中具有不确定性的二分类问题，也是推算目的层是否存在油气资源的技术性问题。本文采用4种贝叶斯网络分类器对准噶尔盆地腹部三工河组地质风险进行预测，得出以下结论：

(1) NB、TAN、AODE和KDB 4种方法在训练集和测试集上的准确度分别均高于85%和82%，说明4种方法的有效性。通过系统分析4种方法表明AODE综合性能最好，说明选择AODE模型作为研究区油气勘探风险预测方法的合理性。

(2) 模型预测符合率达到80%以上，还存在一定的不确定性，根据模型预测数据，结合地质认识，在储量区外，预测出了一些概率大于50%的区域，主要包括三类有利区，其中，A类有利区位于莫索湾凸起东南部和莫北凸起西北部，该类有利区属于扩边类型，把握程度较高，也是下一步油田扩边和滚动勘探的重点区; B类有利区位于莫北凸起和达巴松凸起之间以及东道海子凹陷附近，该类有利区属于前沿未钻探新区，且不确定性相对较高，是下一步风险勘探和甩开勘探的重点区; C类有利区位于石东凸起附近和莫北凸起东北侧。