扩展功能
文章信息
- 韩晓莉, 赵勇, 高文, 马丽华, 宋纪文
- HAN Xiao-li, ZHAO Yong, GAO Wen, MA Li-hua, SONG Ji-wen
- 基于季节性分解的圆形分布法在蚊虫监测数据统计分析中的应用
- Application of circular distribution method based on seasonal decomposition in the statistical analysis of mosquito surveillance data
- 中国媒介生物学及控制杂志, 2021, 32(5): 604-607
- Chin J Vector Biol & Control, 2021, 32(5): 604-607
- 10.11853/j.issn.1003.8280.2021.05.019
-
文章历史
- 收稿日期: 2020-12-15
蚊虫是很多媒介生物性疾病的传播媒介,其密度的高低与蚊媒传染病的流行程度有着密切的关系,由于蚊媒传染病是一个全球性的国际卫生问题,为了更好地掌控蚊虫的种类、数量、分布、季节变化等信息,从而制定全面而合理的蚊媒传染病防控方案,国内外的很多学者都致力于运用新的方法或其他领域的指标,对蚊虫监测结果及蚊媒传染病进行研究和探讨。目前,国内对蚊虫监测结果的分析和统计一般使用描述性分析,通常运用Excel表绘制季节消长曲线,并根据监测结果计算蚊虫种群构成及不同生境密度分布特点等,还有运用地理信息系统(Geographic Information System,GIS)、遥感(Remote Sensing,RS)等技术对监测数据和环境数据进行分析,这些虽然能直观地表现出蚊虫季节消长等基本情况,但未能获得蚊虫季节分布的高峰日、高峰期以及其分布是否具有季节性特征[1];GIS和RS等技术虽然对媒介生物及其相关传染病有较好的监测效果[2-3],但是这些技术与媒介生物性疾病空间流行病学的交叉渗透还处于初步研究阶段[4]。圆形分布法是一种对单峰资料进行季节性特征分析的统计方法,近年来已广泛应用于季节性发生的传染病,尤其是媒介生物性疾病的流行病学调查资料的分析[5-6],并逐渐应用于蚊、蝇等病媒生物监测数据的统计和分析中[7-8]。对蚊虫密度监测结果的科学分析,有利于提早发现蚊虫密度的异常变化,为有效应对蚊媒传染病的发生和流行提供依据。本文将季节分解得出的季节指数加入到圆形分布法,旨在探索分析蚊虫的季节性特征,估测河北省蚊虫密度的高峰日和高峰时段,为制定科学合理的蚊媒精准防控措施提供科学依据。
1 材料与方法 1.1 材料河北省石家庄、唐山、邯郸、秦皇岛等11个市2016-2019年按照《全国病媒生物生态学监测实施方案》诱蚊灯法开展蚊虫监测获得的数据。
1.2 方法应用季节性分解法和圆形分布法进行分析。
1.2.1 季节趋势模型构建[9]采用加法模型来分解长期趋势和季节变动,将河北省蚊虫密度序列分解为:STC(趋势和循环成分,即Tt);SAF(季节成分,即St);和ERR(不规则或随机成分,即It)。
1.2.1.1 模型的构建过程计算季节指数→获得趋势值序列→建立趋势拟合模型→加入季节指数进行预测。
将2016-2019年河北省蚊密度用SPSS 19.0软件进行季节分解:用移动平均法消除季节性变动和不规则变动,得到循环性变动和长期趋势序列值(TC);利用月平均法消除干扰因素,得到季节指数St;以时间序号为自变量,季节调整序列值为因变量,对TC序列进行拟合,构建趋势季节模型。
根据加法模型:Ÿt=Tt+St,其中Ÿt为某月的预测蚊密度,Tt为趋势蚊密度,St为季节指数。
1.2.1.2 St的计算季节指数即时间序列在1个年度内各月份的典型季节特征。St=Y/Tt,Y为蚊密度,Tt为未考虑季节影响的预测值(即趋势蚊密度)。
1.2.1.3 趋势蚊密度(Tt)的计算Tt=a+bt,以时间序列号t为自变量,蚊密度Y为因变量,用最小二乘法可求出a、b 2个参数值:

|
根据统计模型,将分解出来的季节因子加入到圆形分布法中,先将蚊虫监测数据进行角度转化:以1月1日0时为0°角,并依此确定各监测月份的角度,蚊虫密度用月中位角表示。计算公式为:
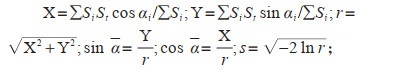
|
当X > 0,Y > 0时,a=arctg(Y/X);当X < 0时,a=180°+arctg(Y/X);当X > 0,Y < 0时,a=360°+arctg(Y/X)。式中,St为季节指数,α为月角度,r为圆形分布离散程度指标,s为角标准差,a为平均角。将度数表示的平均角和角标准差换算出天数,利用a±s对高峰时段做出估测,推算出蚊密度的季节性高峰日和高峰时段。评定标准:r值表示蚊密度在1年内的季节性。r=1,表示最大极限,蚊虫全部集中在某个月出现;r=0,表示最小极限,1年内蚊密度均匀分布在12个月;r > 0.9,有严格季节性;0.7 < r≤0.9,有很强季节性;0.5 < r≤0.7,有明显的季节性;0.3 < r≤0.5,有一定季节性;r≤0.3,季节性差。
1.3 统计学处理圆形分布运用Excel 2007软件建立数据并进行分析,平均角的假设检验采用雷氏Z检验;季节分解法使用SPSS 19.0软件进行分析,用平均相对误差(MRE)来比较原始拟合蚊密度与原始蚊密度的拟合程度,
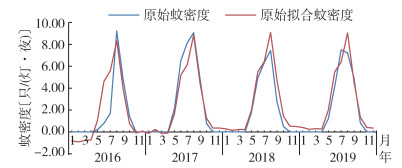
2016-2019年河北省蚊密度均呈现5月开始上升,9月逐渐下降的季节趋势,且均在8月达到高峰,分别为8.33、8.86、9.10和9.05只/(灯·夜)(图 1,原始蚊密度)。2016-2019年平均密度高峰在8月,为8.24只/(灯·夜)。
|
| 图 1 2016-2019年河北省蚊密度和原始拟合的蚊密度对比 Figure 1 Comparison between mosquito density and original fitted mosquito density in Hebei province from 2016 to 2019 |
| |
构建的季节趋势模型(图 2)如下:Ÿt=(1.328+0.072t-0.001t2)+St(Ÿt为某月的预测蚊密度,t为序列号,St为季节指数,F=2.679,P=0.015)。

|
| 图 2 河北省蚊密度季节指数、TC序列值及曲线拟合的TC序列值的对比 Figure 2 Comparison of seasonal index of mosquito density, TC sequence value, and curve-fitted TC sequence value in Hebei province |
| |
通过趋势季节模型获得预测值,用预测值加上季节指数最终得到原始拟合的蚊密度(图 1),t检验结果显示原始拟合蚊密度与原始蚊密度差异无统计学意义(t=-1.456,P=0.189),二者的平均相对误差为7.87%,原始拟合蚊密度与原始蚊密度的走向基本一致。
2.3 圆形分布由季节分解获得季节指数见表 1,河北省蚊密度在1年内呈单峰分布,在每年的6-8月达到密度高峰,符合圆形分布法的应用条件。r=0.812,平均角a=210.11°,角标准差为89.06°。对a进行雷氏Z检验,P < 0.001,平均角有意义,蚊密度存在集中趋势,2016-2019年河北省平均蚊密度高峰日为8月2日,平均高峰期为6月27日至9月5日。
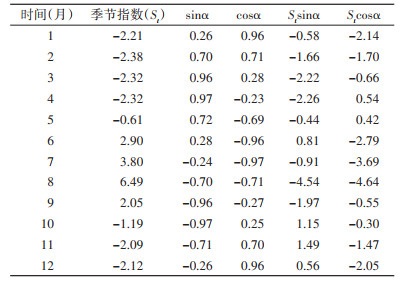
|
在分析蚊虫监测数据时,目前最常用的方法是以图表的形式描述,即用月密度作成曲线图,以峰值的高低表示蚊虫密度的多少,这种方法简便、直观,但是不能确定其确切的密度高峰日和高峰期;用圆形分布法对病媒生物密度进行统计分析具有简捷、准确等诸多优点[11-14],可以方便地推测病媒生物密度的高峰日和高峰时段[14],但由于蚊虫监测数据会受到监测人员、布灯位置及监测时间等因素的影响,如果不剔除这些非季节性因素的影响,而直接使用圆形分布法对蚊密度分布的季节特征进行分析,会对分析结果产生不同程度的影响[15]。季节分解的目的就是对季节性特征进行识别、提取,如果将季节分解法分解出的季节指数加入到圆形分布法中,通过二者的综合运用对蚊虫密度进行统计分析,就可以剔除监测人员、监测时间等非季节因素的影响,更加准确地推测出蚊虫密度的高峰日和高峰时段。笔者使用该方法对2016-2019年河北省蚊虫季节特征进行分析发现,蚊虫密度的r值为0.812,P < 0.001,说明河北省蚊虫密度具有很强的季节性,且均呈现先升后降的季节趋势。以1年为一个周期,每个周期内蚊密度均呈单峰分布,蚊密度趋势分析结果与描述性图表的分析结果相一致[16],说明基于季节性分解的圆形分布法对蚊虫密度的季节性分析是适用的。通过分析结果可知,河北省蚊密度平均高峰日为8月2日,平均高峰期为6月27日至9月5日,提示应在蚊虫密度高峰期前的6月上中旬采取合理措施,有效控制蚊虫孳生地,以降低蚊媒传染病的传播和流行。综上所述,数据序列满足圆形分布法的条件时,基于季节性分解的圆形分布法可以应用于对蚊虫监测数据的分析[15],尤其适用于蚊虫的季节性分析,可以合理估测蚊虫密度高峰期,为制定蚊虫防制措施提供科学依据。
需要说明的是圆形分布仅适用于单峰性资料,并需要将具体单位换算为角度,如1 h相当于15°,1 min相当于0.25°,只有满足这些条件的资料,再通过季节分解法得到的季节指数利用圆形分布进行统计分析,才能合理预测蚊虫密度的高峰日和高峰期。
| [1] |
罗林峰, 王德全. 圆形分布法及生物多样性指标在蚊蝇等监测中的应用[J]. 中国热带医学, 2014, 14(1): 121-124. Luo LF, Wang DQ. Application of circular distribution method and biodiversity indicators in monitoring of mosquitoes flies and other vectors[J]. China Trop Med, 2014, 14(1): 121-124. DOI:10.13604/j.cnki.46-1064/r.2014.01.009 |
| [2] |
Jacob BG, Burkett-Cadena ND, Luvall JC, et al. Developing GIS-based eastern equine encephalitis vector-host models in Tuskegee, Alabama[J]. Int J Health Geogr, 2010, 9(1): 12. DOI:10.1186/1476-072X-9-12 |
| [3] |
Jacob BG, Muturi EJ, Caamano EX, et al. Hydrological modeling of geophysical parameters of arboviral and protozoan disease vectors in internally displaced people camps in Gulu, Uganda[J]. Int J Health Geogr, 2008, 7(1): 11. DOI:10.1186/1476-072X-7-11 |
| [4] |
何隆华, 周明浩, 褚宏亮, 等. 遥感技术在蚊媒传染病研究中的应用进展[J]. 中国媒介生物学及控制杂志, 2014, 25(2): 184-188. He LH, Zhou MH, Chu HL, et al. Application of remote sensing technology in research on mosquito-borne diseases: a review[J]. Chin J Vector Biol Control, 2014, 25(2): 184-188. DOI:10.11853/j.issn.1003.4692.2014.02.028 |
| [5] |
毛明飞. 灌云县2010-2019肾综合征出血热流行病学特征[J]. 江苏预防医学, 2020, 31(5): 537-538. Mao MF. Epidemiological characteristics of hemorrhagic fever with renal syndrome in Guanyun county from 2010 to 2019[J]. Jiangsu J Prev Med, 2020, 31(5): 537-538. DOI:10.13668/j.issn.1006-9070.2020.05.022 |
| [6] |
宋仙保, 郭建花, 张世勇. 1949-2018年石家庄市流行性乙型脑炎发病趋势分析[J]. 中国人兽共患病学报, 2019, 35(11): 1047-1050. Song XB, Guo JH, Zhang SY. Epidemic trend of Japanese encephalitis in Shijiazhuang city, China, 1949-2018[J]. Chin J Zoonoses, 2019, 35(11): 1047-1050. DOI:10.3969/j.issn.1002-2694.2019.00.167 |
| [7] |
刘丽军, 施文平, 席韵, 等. 应用圆形分布法分析闵行区蝇类密度季节消长规律[J]. 热带医学杂志, 2012, 12(8): 1019-1021. Liu LJ, Shi WP, Xi Y, et al. Seasonal change analysis of flies in Minhang district, Shanghai from 2006 to 2010 by circular distribution method[J]. J Trop Med, 2012, 12(8): 1019-1021. |
| [8] |
毛龙飞, 韦悦, 裘剑飞. 圆形分布法在蝇类季节消长规律中的应用[J]. 中国媒介生物学及控制杂志, 2007, 18(6): 456-458. Mao LF, Wei Y, Qiu JF. Application of circular distribution method to probe the seasonal change of flies[J]. Chin J Vector Biol Control, 2007, 18(6): 456-458. DOI:10.3969/j.issn.1003-4692.2007.06.008 |
| [9] |
杨亮. 临沂市手足口病发病率的趋势季节模型预测研究[J]. 社区医学杂志, 2015, 13(17): 13-15. Yang L. Research on forecasting of hand-foot-mouth disease incidence in Linyi by the trend season model[J]. J Commun Med, 2015, 13(17): 13-15. |
| [10] |
付凌姣, 马建新, 葛申, 等. 应用集中度和圆形分布法分析2016-2018年北京市朝阳区手足口病季节性特征[J]. 中国病毒病杂志, 2020, 10(4): 289-292. Fu LJ, Ma JX, Ge S, et al. Concentration and circular distribution-based analyses of the seasonal characteristics of hand, foot and mouth disease from 2016 to 2018 in Chaoyang district of Beijing, China[J]. Chin J Viral Dis, 2020, 10(4): 289-292. DOI:10.16505/j.2095-0136.2020.0009 |
| [11] |
尚文旭, 海秀萍, 秦丰程. 圆形分布法在探讨蝇类季节消长规律中的应用[J]. 中国媒介生物学及控制杂志, 2005, 16(1): 17-18. Shang WX, Hai XP, Qin FC. Application of the round distribution method to probe the seasonal change of flies[J]. Chin J Vector Biol Control, 2005, 16(1): 17-18. DOI:10.3969/j.issn.1003-4692.2005.01.005 |
| [12] |
许筱红, 佘桂芝, 唐月娥, 等. 圆形分布法分析江苏省传疟按蚊季节性消长规律变化[J]. 中国卫生统计, 2014, 31(6): 990-991. Xu XH, She GZ, Tang YE, et al. Analysis of seasonal changes of Anopheles malaria mosquitoes in Jiangsu province by circular distribution method[J]. Chin J Health Stat, 2014, 31(6): 990-991. |
| [13] |
何业计, 闫清源, 尔夏提江·阿迪力江, 等. 2005-2017年全国3种主要蚊媒传染病发病数的圆形分布分析[J]. 上海交通大学学报(农业科学版), 2019, 37(2): 14-18. He YJ, Yan QY, Erxat A, et al. Circular distribution of the incidences of three mosquito-borne infectious diseases in China from 2005 to 2017[J]. J Shanghai Jiaotong Univ(Agric Sci), 2019, 37(2): 14-18. DOI:10.3969/J.ISSN.1671-9964.2019.02.003 |
| [14] |
蒋莹, 徐哲, 许旭红. 应用圆形分布法探讨建德市病媒生物季节性消长规律[J]. 中国媒介生物学及控制杂志, 2014, 25(5): 474-475. Jiang Y, Xu Z, Xu XH. Application of circular distribution method in investigation of seasonal fluctuation of vectors in Jiande, China[J]. Chin J Vector Biol Control, 2014, 25(5): 474-475. DOI:10.11853/j.issn.1003.4692.2014.05.025 |
| [15] |
王永斌, 柴峰, 李向文, 等. 基于周期分解的圆形分布法分析我国流行性乙型脑炎季节特征[J]. 郑州大学学报(医学版), 2016, 51(4): 486-489. Wang YB, Chai F, Li XW, et al. Application of circular distribution method based on seasonal decomposition in analysis on seasonal feature of epidemic encephalitis B in China[J]. J Zhengzhou Univ(Med Sci), 2016, 51(4): 486-489. DOI:10.13705/j.issn.1671-6825.2016.04.013 |
| [16] |
高文, 黄钢, 韩晓莉. 基于蚊密度差分自回归移动平均模型预测流行性乙型脑炎的贝叶斯判别分析研究[J]. 中国媒介生物学及控制杂志, 2018, 29(6): 557-563. Gao W, Huang G, Han XL. Application of Bayes analysis in Japanese encephalitis prediction based on multiple seasonal autoregressive integrated moving average model[J]. Chin J Vector Biol Control, 2018, 29(6): 557-563. DOI:10.11853/j.issn.1003.8280.2018.06.003 |
 2021, Vol. 32
2021, Vol. 32


