中国媒介生物学及控制杂志  2021, Vol. 32 Issue (3): 339-343,364
|
蚊媒传染病是由蚊类传播病原体导致的一类传染病。成蚊密度具有一定的季节性，是蚊媒传染病发生的重要因素之一[1-2]。蚊媒传染病的防控需要建立在准确的成蚊密度季节消长趋势研判和科学的防蚊灭蚊决策之上。因此，成蚊密度是重要的病媒生物监测和评价指标。研究表明，成蚊密度与气温、降水、湿度等气象因素存在一定程度的关联[3-4]。人工智能算法领域的快速发展，有助于将表观抽象的关联转变为直观具体的函数模型，揭示多者之间存在的自然规律[5-6]。本研究尝试通过多元线性回归（multiple linear regression algorithm，MLR）和基因表达式编程（gene expression programming，GEP）算法，探讨成蚊密度与气象因素之间的关系，建立可用于成蚊密度预测的函数模型。
1 材料与方法 1.1 数据来源数据来自青岛市2016－2019年3－11月的成蚊密度监测资料。按照《全国病媒生物监测实施方案》（中疾控传防发〔2016〕56号）[7]要求，在青岛市10个区（市）的居民区、公园、医院、农村民房、牲畜棚等生境分别选择2处开展成蚊密度监测，每月开展2次，相邻2次测定间隔时间不少于10 d。监测时，将诱蚊灯挂于室外避风的场所，光源距离地面1.5 m，远离干扰光源。于日落前1 h接通电源，开启诱蚊灯诱捕蚊虫，直至次日日出后1 h关闭电源，将集蚊袋取出，于冰箱冷冻处死捕获的蚊虫，并进行计数，鉴定种类、性别，根据该月监测布放总灯数、总诱灯夜数和捕获总雌蚊数计算成蚊密度。计算公式如下：
|
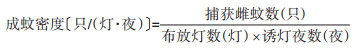
气象资料由中国气象局官方网站获得[8]，该网站公开发布了青岛市每日的气温、湿度、降水等信息。本文收集整理了成蚊监测月份的月最高气温、月最低气温、月平均气温、月平均湿度、月累计降水量和月累计降水天数6种地面气象数据资料做为函数预测模型的自变量，当月的成蚊密度为因变量。将2016－2018年的6种气象数据和成蚊密度数据作为训练集，分别采用多元线性回归算法和基因表达式编程算法建立2种不同的成蚊密度回归预测模型。外部验证时，2019年的气象和成蚊密度数据作为测试集，将6种气象数据代入新建立的2个成蚊密度预测模型计算理论的蚊密度，并与2019年实际监测的成蚊密度作比较，检验模型的预测能力。
1.2 多元线性回归算法多元线性回归算法在很多研究领域有着广泛的应用，是数据挖掘的重要方法。在成蚊密度预测中，利用函数关系式，由自变量气象资料数据计算因变量成蚊密度数值，得到预测的成蚊密度。该方法的多元线性回归数学模型在本研究中表示为：
|
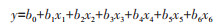
式中，b0为常数项，b1、b2、b3、b4、b5、b6为偏回归系数，表示在其他自变量固定的条件下，xi改变1个单位时应变量的改变量。x1、x2、x3、x4、x5、x6分别代表月最高气温、月最低气温、月平均气温、月平均湿度、月累计降水量和月累计降水天数。最后，该模型在SPSS 17.0软件中构建生成。
多元线性回归模型建立的成蚊密度预测模型，有2个方面的检验：（1）拟合度检验；（2）回归方程的显著性检验。拟合度检验主要应用决定系数R2（0≤R2≤1），公式为：
|
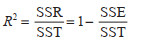
式中，SSR为回归平方和，SSE为残差平方和，SST为离差平方和。R2越接近1，则拟合度越好，越接近0，拟合度越差。通常，R2≥0.85的回归方程模型可用于进行成蚊密度的预测分析[9]。
回归方程和回归系数的统计学显著性检验以P < 0.05表示差异有统计学意义。模型的预测性能采用相关系数（r）和方差（S2）检验，由SPSS 17.0软件计算生成。同时采用2019年3－11月的6种气象数据和成蚊密度数据作为测试集对该模型的预测能力进行外部验证。
1.3 基因表达式编程算法基因表达式编程算法是一种典型的非线性回归分析方法，该算法通过模拟基因的遗传规律，以基因组为单位，借助线性染色体来表达数学函数[10-11]。该算法吸收了遗传算法和遗传程序设计的优点，以固定长度的线性编码表示个体，从而提升了遗传操作效率，具备更强的函数挖掘和探索能力。气象因素与成蚊密度间除了线性关系外，可能存在某种非线性的关系。因此，本文尝试借助非线性的函数挖掘方法揭示两者之间的函数关系。
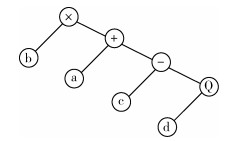
GEP算法由染色体和表达式树2部分组成。在研究中，月最高气温、月最低气温、月平均气温、月平均湿度、月累计降水量、月累计降水天数将分别作为算法的染色体部分，具体的某种气象数值将作为基因进一步构成该类染色体。通过含有多基因新构成的染色体变异、基因倒置、基因重组等方式，可以使函数关系发生改变，最后编码、运算形成非线性函数模型。表达式树用来表达不同气象染色体间的编码信息，可以体现每个染色体的位置排列及与其他染色体的函数关系，进一步可转换为函数关系方程式。例如，如图 1所示的表达式树，可以用函数F=b*（a+（c-sqrt（d）））表示，a、b、c、d分别代表 4种不同的染色体。那么，本研究中选择了6种气象参数，将分别作为6种不同的染色体构建预测模型，最后模型的表达式树可以进一步转化为预测方程式来展示。本次研究应用的分析软件GeneXproTools 5.0下载于网站gepsoft（www.gepsoft.com/gxpt.htm），数据将在该软件中进行各种方式的编码排列组合，最终将获得最佳的函数预测模型。软件中固定参数栏目的不同数值将会影响预测结果。设置的部分参数中，尝试次数：单次建模尝试次数；连接函数：建立的分段函数间的连接关系；代内变异数：未改变的单次建模变异运算次数；突变率：染色体内基因的突变概率；基因重组率：染色体内基因重新组合概率；倒置率：染色体倒置概率；基因移位率：染色体内基因移位概率；精确度：函数模型检验精确度。经过多次调整参数后获得最佳预测模型，本研究的参数设置见表 1。模型的预测性能采用相关系数和方差检验，同时采用测试集对模型的预测能力进行外部验证。
|
| 图 1 基因表达式树 Figure 1 Gene expression tree |
| |
|
相关分析结果显示，2016－2019年3－11月青岛市成蚊密度监测值与月最高气温、月最低气温、月平均气温、月累计降水量、月平均湿度、月累计降水天数呈正相关关系，差异有统计学意义（r1=0.84，P=0.001；r2=0.86，P=0.001；r3=0.83，P=0.001；r4=0.78，P=0.001；r5=0.81，P=0.001；r6=0.41，P=0.013）。
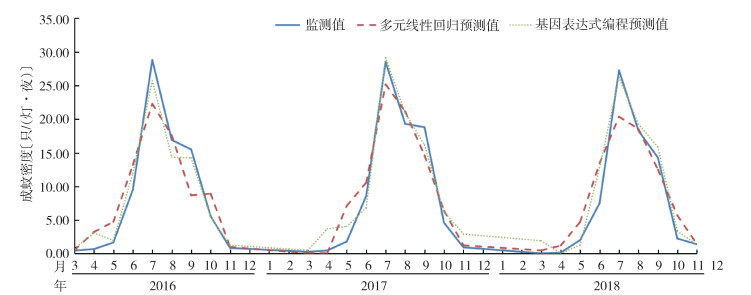
2.2 MLR模型预测结果基于SPSS 17.0软件，采用多元线性回归方法对成蚊密度和气象资料进行分析，得到预测模型的R2为0.89，调整后的R2为0.87，大于经验值0.85，显示拟合度较好；在回归方程的显著性检验中，所建方程模型有统计学意义（F=20.942，P=0.001），预测值与监测值的折线图对比基本达到了吻合状态（图 2）。训练集预测结果与监测成蚊密度之间，r=0.94，P=0.001，S2=3.36。所建模型方程如下：
|
|
| 注：监测值为2016－2018年3－11月监测的成蚊密度。 图 2 多元线性回归算法和基因表达式编程算法模型训练集预测值与监测值比较 Figure 2 Prediction values (in the training set of multiple linear regression algorithm and gene expression programming algorithm models) vs surveillance values |
| |
式中，x1、x2、x3、x4、x5、x6分别表示月最高气温、月最低气温、月平均气温、月累计降水量、月平均湿度和月累计降水天数。基于该线性回归方程对青岛市2019年3－11月成蚊密度测试集进行预测，测试集预测结果与实际监测成蚊密度之间，r=0.93，P=0.001，S2=3.35。预测结果见表 2，吻合情况见图 3。
|
|
| 图 3 多元线性回归算法和基因表达式编程算法模型2019年3－11月成蚊密度预测值与监测值比较 Figure 3 Prediction values (in multiple linear regression algorithm and gene expression programming algorithm models) vs surveillance values of adult mosquito density from March to November, 2019 |
| |
建立预测蚊密度的线性方程后，以相同的自变量、因变量作为GEP算法的参数建立非线性方程。GEP算法软件包易于操控，模型可随时通过测试集检验优劣，优化过程更加直观便捷。本次研究的函数集为“+，-，×，/，sin”，通过266次优化后建立了最佳非线性方程模型，预测结果吻合情况见图 2。所建GEP模型方程如下：
|
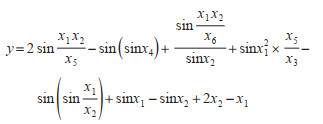
式中，x1、x2、x3、x4、x5、x6分别表示月最高气温、月最低气温、月平均气温、月累计降水量、月平均湿度和月累计降水天数。
GEP算法训练集预测结果与监测成蚊密度之间，r=0.97，P=0.001，S2=1.95。基于该线性回归方程对青岛市2019年3－11月成蚊密度测试集进行预测，测试集预测结果与监测成蚊密度之间，r=0.96，P=0.001，S2=1.03。预测结果见表 2，吻合情况见图 3。
3 讨论蚊虫是重要的医学昆虫之一，能传播疟疾、登革热、流行性乙型脑炎（乙脑）和寨卡病毒病等蚊媒传染病。蚊虫的生存、发育、行为以及生态学受气象因素的影响极大。本文研究显示，月最高气温、月最低气温、月平均气温、月累计降水量、月平均湿度和月累计降水天数6个气象因素是影响成蚊生长的关键正相关因素，能够促进媒介的生长从而提高其密度。影响成蚊密度的多种因素之间往往存在着复杂的关系，简单的因果结构模型很难揭示其流行趋势。随着数学模型和信息技术的发展，人工智能算法预测模型已经在成蚊密度的短期预测中得到了初步尝试。吴崧霖等[12]运用支持向量机算法预测深圳市坪山区成蚊密度，潘衍宇等[13]基于R语言自回归积分移动平均模型来预测广州市白纹伊蚊（Aedes albopictus）密度，刘起勇[6]表示基于多学科模型的预测，已成为当前病媒生物监测预警最常用的方法。
成蚊密度变化受到气象因素的影响，其中温度、降水量、湿度是影响成蚊密度的关键因素[6, 14-15]。因此，利用气象因素对成蚊密度季节消长情况进行预测较为合适。本次研究采用的MLR算法训练集r为0.94，测试集r为0.93；GEP算法训练集r为0.97，测试集r为0.96，2种模型中的因变量成蚊密度与自变量气象因素的拟合优度均较好，所建回归方程预测模型效果较为理想。由表 2和图 3可以看出，GEP预测模型的相对误差最小，预测值最接近于真实值，预测准确度明显高于MLR预测模型。由此可见，GEP预测模型具有较高的预测准确度。蚊密度与气象因素存在内部复杂、指标和因素较多的非线性关系。GEP作为一种通用的自适应随机搜索算法[16-17]，在没有任何先验知识、不了解事物内部机制的情况下，对于复杂、多输入、不确定的非线性问题具有较强的映射能力，在预测和函数挖掘中具有优异的表现能力[18-21]。
加强媒介成蚊密度监测和控制，是遏制蚊媒疾病传播和流行的有效手段。而通过建立蚊密度的预测，提前了解密度变化趋势，有利于主动开展灭蚊、防蚊工作，可以降低包括乙脑、登革热等在内的蚊传疾病的发生、传播和流行风险。随着人工智能算法和大数据模块的快速发展，未来更加准确、适应度更广的预测模型将会运用到病媒生物防制的各个领域。
利益冲突 无
| [1] |
高文, 黄钢, 韩晓莉. 基于蚊密度差分自回归移动平均模型预测流行性乙型脑炎的贝叶斯判别分析研究[J]. 中国媒介生物学及控制杂志, 2018, 29(6): 557-563. Gao W, Huang G, Han XL. Application of Bayes analysis in Japanese encephalitis prediction based on multiple seasonal autoregressive integrated moving average model[J]. Chin J Vector Biol Control, 2018, 29(6): 557-563. DOI:10.11853/j.issn.1003.8280.2018.06.003 |
| [2] |
赵宁, 郭玉红, 吴海霞, 等. 2019年全国媒介蚊虫监测报告[J]. 中国媒介生物学及控制杂志, 2020, 31(4): 395-400, 406. Zhao N, Guo YH, Wu HX, et al. National vector surveillance report on mosquitoes in China, 2019[J]. Chin J Vector Biol Control, 2020, 31(4): 395-400, 406. DOI:10.11853/j.issn.1003.8280.2020.04.003 |
| [3] |
高文, 马丽华, 黄钢, 等. 河北省2013-2015年蚊媒传染病与蚊密度相关性分析[J]. 中国媒介生物学及控制杂志, 2016, 27(4): 350-353. Gao W, Ma LH, Huang G, et al. Analysis on correlation between mosquito-borne diseases and seasonality of mosquito density in Hebei province from 2013 to 2015[J]. Chin J Vector Biol Control, 2016, 27(4): 350-353. DOI:10.11853/j.issn.1003.8280.2016.04.009 |
| [4] |
赵奇, 高丽君, 郭祥树, 等. 河南省2016年白纹伊蚊幼虫监测结果分析[J]. 中国媒介生物学及控制杂志, 2018, 29(4): 358-360. Zhao Q, Gao LJ, Guo XS, et al. Analysis on surveillance results of Aedes albopictus larvae in Henan province in 2016[J]. Chin J Vector Biol Control, 2018, 29(4): 358-360. DOI:10.11853/j.issn.1003.8280.2018.04.009 |
| [5] |
吕锡宏, 王瑞平, 郭晓芹, 等. 移动平均法的季节趋势模型在白纹伊蚊密度预测中的应用[J]. 中华卫生杀虫药械, 2019, 25(3): 247-250. Lyu XH, Wang RP, Guo XQ, et al. Application of seasonal trend model based on moving average method in predicting density of Aedes albopictus[J]. Chin J Hyg Insect Equip, 2019, 25(3): 247-250. DOI:10.19821/j.1671-2781.2019.03.015 |
| [6] |
刘起勇. 病媒生物监测预警研究进展[J]. 疾病监测, 2018, 33(2): 123-128. Liu QY. Research progress on the vector surveillance and early-warning[J]. Dis Surveil, 2018, 33(2): 123-128. DOI:10.3784/j.issn.1003-9961.2018.02.005 |
| [7] |
中国疾病预防控制中心. 全国病媒生物监测实施方案[Z]. 北京: 中国疾病预防控制中心, 2016. Chinese Center for Disease Control and Prevention. National vector surveillance implementation plan[Z]. Beijing: Chinese Center for Disease Control and Prevention, 2016. |
| [8] |
中国气象局. 天气预报[EB/OL]. (2019-11-30)[2020-06-22]. https://weather.cma.cn. China Meteorological Administration.Weather forecast[EB/OL]. (2019-11-30)[2020-06-22]. https://weather.cma.cn. |
| [9] |
艾洪福. 基于MLR模型的雾霾天气预测研究[J]. 农业与技术, 2019, 39(22): 148-150. Ai HF. Research on haze weather prediction based on MLR model[J]. Agric Technol, 2019, 39(22): 148-150. DOI:10.19754/j.nyyjs.20191130058 |
| [10] |
Guven A, Aytek A. New approach for stage-discharge relationship: gene-expression programming[J]. J Hydrol Eng, 2009, 14(8): 812-820. DOI:10.1061/(ASCE)HE.1943-5584.0000044 |
| [11] |
Melo-Filho CC, Dantas RF, Braga RC, et al. QSAR-driven discovery of novel chemical scaffolds active against Schistosoma mansoni[J]. J Chem Inf Model, 2016, 56(7): 1357-1372. DOI:10.1021/acs.jcim.6b00055 |
| [12] |
吴崧霖, 吴能简, 何志明, 等. 支持向量机在深圳市坪山区成蚊密度预测中的应用[J]. 医学动物防制, 2020, 36(3): 208-221. Wu SL, Wu NJ, He ZM, et al. Application of support vector machine in adult mosquito density prediction in Pingshan district, Shenzhen city[J]. J Med Pest Control, 2020, 36(3): 208-221. DOI:10.7629/yxdwfz202003002 |
| [13] |
潘衍宇, 吴海霞, 国佳, 等. 基于R语言自回归积分移动平均模型的广州市白纹伊蚊密度预测研究[J]. 中国媒介生物学及控制杂志, 2018, 29(6): 545-549. Pan YY, Wu HX, Guo J, et al. Population density prediction of Aedes albopictus in Guangzhou based on autoregressive integrated moving average model[J]. Chin J Vector Biol Control, 2018, 29(6): 545-549. DOI:10.11853/j.issn.1003.8280.2018.06.001 |
| [14] |
王晓中, 孙时, 耿丽梅, 等. 气候变化对媒介传播传染病影响的区域分析及应对措施[J]. 中国国境卫生检疫杂志, 2011, 34(2): 134-138. Wang XZ, Sun S, Geng LM, et al. Regional analysis on influence of climate changes to vector-borne infections and its countermeasures[J]. Chin J Front Health Quarantine, 2011, 34(2): 134-138. DOI:10.16408/j.1004-9770.2011.02.003 |
| [15] |
何玉兰, 杨菂子, 李晓宁, 等. 主要气候因素变化影响2017-2018年广州蚊密度与登革流行趋势分析[J]. 现代预防医学, 2020, 47(9): 1570-1574. He YL, Yang DZ, Li XN, et al. Mosquito density and dengue epidemic trend affected by the change of main climate factors, Guangzhou, 2017-2018[J]. Mod Prev Med, 2020, 47(9): 1570-1574. |
| [16] |
马竹根. 基因表达式编程在公路货运量预测中的应用[J]. 现代计算机, 2009(6): 87-89. Ma ZG. Model of highway freight forecasting based on gene expression programming[J]. Mod Comput, 2009(6): 87-89. DOI:10.3969/j.issn.1007-1423-B.2009.06.026 |
| [17] |
Li Y, Chen X, He DJ, et al. Research on GEP algorithm and its applications in foodstuff yield prediction from Shaanxi province[C]//Proceedings of 2008 International Conference on Advanced Computer Theory and Engineering. Phuket, Thailand: IEEE, 2009: 690-693.
|
| [18] |
郭勇, 何锫, 张国锋, 等. 基于表现型的基因表达式编程解空间模型研究[J]. 工程科学与技术, 2017, 49(5): 117-126. Guo Y, He P, Zhang GF, et al. Gene expression programming solution space model based on phenotype[J]. Adv Eng Sci, 2017, 49(5): 117-126. DOI:10.15961/j.jsuese.201601393 |
| [19] |
宋富成, 崔莲花, 朴金梅, 等. 基于启发式和基因表达式编程算法预测离子液体的pEC50值[J]. 青岛大学医学院学报, 2017, 53(3): 312-316, 319. Song FC, Cui LH, Piao JM, et al. Prediction of pEC50 of ionic liquids based on heuristic method and gene expression programming algorithm[J]. Acta Aacad Med Qingdao Univ, 2017, 53(3): 312-316, 319. DOI:10.13361/j.qdyxy.201703017 |
| [20] |
曹维, 林毅申. 连续编码的基因表达式编程算法[J]. 计算机工程与设计, 2017, 38(3): 682-686, 734. Cao W, Lin YS. Gene expression programming algorithm based on serial coding[J]. Comput Eng Desig, 2017, 38(3): 682-686, 734. DOI:10.16208/j.issn1000-7024.2017.03.023 |
| [21] |
王超学, 张婧菁, 吴书玲. 采用混合策略的改进基因表达式编程[J]. 计算机科学与探索, 2017, 11(1): 163-170. Wang CX, Zhang JJ, Wu SL. Improved gene expression programming algorithm used by hybrid strategy[J]. J Front Comput Sci Technol, 2017, 11(1): 163-170. DOI:10.3778/j.issn.1673-9418.1509046 |
表1(Table 1)
