蚤类属于节肢动物门、昆虫纲、蚤目。迄今全世界已发现约2 574种(亚种)，分布遍及全球，从赤道沙漠，经过热带雨林远至南北极冰原。我国已发现蚤类655种(亚种)。由于蚤类侵袭和吸血，可在人、畜间直接引起骚扰、皮炎、贫血，更重要的是其可作为传播鼠疫、地方性(鼠型)斑疹伤寒等重要疾病的媒介。因此，蚤类是重要的医学害虫类群之一。依据采集途径和方法不同，人为地将蚤类分为鼠体蚤、洞干蚤和鼠巢蚤。河北省鼠疫自然疫源地自1971年12月26日首次从自毙的长爪沙鼠(Meriones unguiculatus)体内分离出鼠疫耶尔森菌(鼠疫菌)，证实其存在以来，共计发生动物间疫情5次，其中2002年曾在长爪沙鼠巢中检获疫蚤13匹^[1]，长爪沙鼠巢蚤在动物鼠疫流行期间扮演着尤为重要的角色。蚤类季节性数量变化通常是由季节消长曲线来描述^[2]，该方法虽然能显示季节消长过程，但不能以某个指标的形式显示季节消长的规律和特点，还停留在描述生物学的阶段，不便于开展量化以及相关的分析研究。虽能在一定程度上反映出蚤类的季节消长规律，但受样本量的影响显著。

向量合成表示法—集中度(M)说明传染病的群体现象在1年中的集中程度，其最常用于水文、气象学等学科领域，近几年，集中度法逐渐应用到传染病季节性分布^[3-4]、疾病的时间聚集性^[5]及道路交通伤害发生时间规律^[6]的研究上。圆形分布法用于角度、昼夜时间等资料的分析，通过三角函数变换，使得原始资料成为线性资料，目前广泛应用于疾病发病规律^[7]、媒介生物的季节消长^[8]等方面研究。2种方法均不受样本量的影响，其综合全年各月的发病或发生情况，能够比较真实地反映某种疾病或现象在全年的集中程度。本文拟采用集中度及圆形分布法对2016-2019年河北省鼠疫疫源地康保牧场监测点长爪沙鼠巢蚤的调查结果进行探讨，以寻求一种较为准确、量化地显示蚤类数量季节性变化的数据分析方法。

数据来自河北省鼠疫防治所康保牧场监测点2016-2019年的鼠疫监测月报数据。

巢蚤的数量通过调查宿主动物栖息巢穴的巢蚤指数来反映。河北省长爪沙鼠鼠疫疫源地康保牧场鼠疫监测点每月有计划地挖掘主要宿主动物长爪沙鼠窝巢3~5个，挖到窝巢时，迅速将全部窝巢草和巢内浮土一起装入鼠口袋中，做好标记，带回实验室，置于白瓷盆中，进行检蚤、分类。

集中度(M)说明传染病的群体现象在1年中的集中程度。M值为1时，表示最大极限，说明1年内的疾病总数集中在1个月内；M值为0时，表示最小极限，说明1年内的疾病总数均匀分布在12个月内；M≥0.9时，说明疾病有严格的季节性；0.7≤M值< 0.9，说明疾病有很强的季节性；0.5≤M值< 0.7，说明疾病有较强的季节性；0.3≤M值< 0.5，说明疾病有一定的季节性；M值< 0.3，说明疾病的时间分布比较均匀。

用上述资料计算月捡巢蚤数与其全年捡蚤数总和之比，然后按下列公式计算集中度。

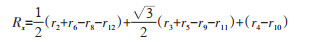
(1)

(2)

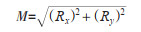
(3)

式中，M表示集中度，r表示某月捡巢蚤数与其全年捡巢蚤总和之比，下角标表示月份。

根据蚤指数公式，平均蚤指数=获蚤数/调查鼠巢数，计算各月的平均蚤指数。将蚤指数作为理论频数代替实际频数进行运算。

用圆分布平均角a表示蚤数量增长时间的集中方向。将增长时间换算成角度，然后通过三角函数代换，求出长爪沙鼠巢蚤数量增长的集中时间、离散程度及其高峰期。

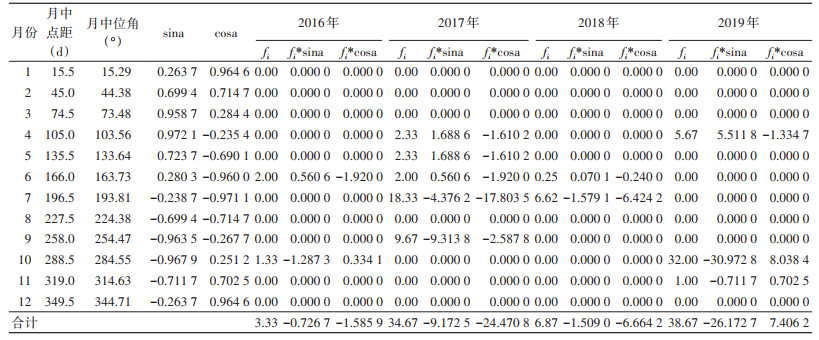
先求出各月份的中点值，以1月1日0时为起点，则1月有31 d，月中点距0为15.5 d，2月有28 d，月中点距0为31+14=45 d，以此类推。再将时间换算成角度，全年365 d，相当于圆周360°，则1 d相当于0.986 3°。1月中点为15.5 d，则中位角为15.5×0.986 3=15.29°，再通过三角函数原理则可求出长爪沙鼠巢蚤密度增长的集中时间和增长高峰期，其计算公式为：

(4)

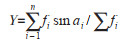
(5)

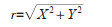
(6)

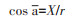
(7)

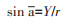
(8)

式中，f_i指长爪沙鼠巢蚤月平均蚤指数，a_i指第i月的平均角度，r指圆形分布集中趋势值，a指平均角。

(1) 2个样本角均数的比较：2个样本角均数的比较采用Watson-Williams检验，按公式(9)计算统计量F值，做F检验。

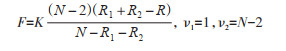
(9)

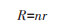
(10)

式中，N为2个样本含量n₁及n₂之和，R₁和R₂由2个样本分别按公式(10)计算得出；R为2个样本合并后求出的R值；K为计算F值的校正因子。

(2) 多个样本角均数的比较：上述Watson-Williams检验可推广到多个样本角均数的比较，但需按公式(11)计算统计量F值。

(11)

式中，k为样本个数，R_j为各样本分别按式(10)计算的R值，其和为∑R_j，R为k个样本合并后求得的R值，N为各个样本含量的和，K为校正因子。

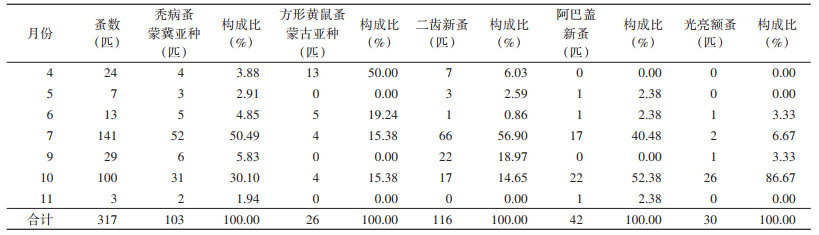
2016-2019年康保牧场鼠疫监测点共计调查长爪沙鼠窝巢138个，染蚤窝巢35个，染蚤率为25.36%，获蚤317匹，平均蚤指数为2.30，隶属于3科4属5种，其中以二齿新蚤(Neopsylla bidentatiformis)最多为116匹，秃病蚤蒙冀亚种(Nosopsyllus laeviceps kuzenkovi)103匹次之，阿巴盖新蚤(N. abagaitui)、光亮额蚤(Frontopsylla luculenta)和方形黄鼠蚤蒙古亚种(Citellophilus tesquorurn mongolicus)较少。见表 1。

表 1 2016-2019年河北省鼠疫自然疫源地长爪沙鼠巢蚤调查结果 Table 1 Data of Meriones unguiculatus nest fleas in a natural plague focus of Hebei province, 2016-2019

表选项

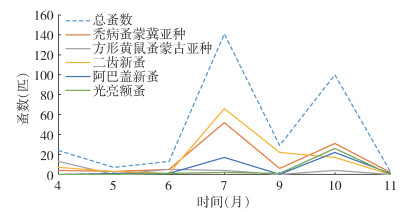
除1、2、12月未开展长爪沙鼠巢蚤调查外，其他各月均进行了调查，其中3和8月未捡获蚤。全年捡蚤以7月最多，获蚤141匹(占44.48%)，其次是10月，获蚤100匹(占31.55%)；再次是9月，获蚤29匹(占9.15%)(表 2)。二齿新蚤除11月未捡获，其他月份均可获得，以7月最多，其次是9月，呈双峰型；秃病蚤蒙冀亚种全年均可捡获，其中以7月最高，10月次之，呈双峰型；阿巴盖新蚤亦呈双峰型，其高峰出现在7和10月；光亮额蚤仅在6、7、9和10月捡获，其中10月最多，呈单峰型；方形黄鼠蚤蒙古亚种仅在4、6、7和10月检获蚤，其中以4月最高，呈单峰型。见图 1。

表 2 2016-2019年河北省鼠疫自然疫源地各月份调查长爪沙鼠巢蚤蚤种构成比 Table 2 Species composition of Meriones unguiculatus nest fleas in a natural plague focus of Hebei province, each month of 2016-2019

表选项

图 1 河北省鼠疫自然疫源地长爪沙鼠巢蚤蚤种数量分布 Figure 1 Distributions of numbers of different species of Meriones unguiculatus nest fleas in a natural plague focus of Hebei province

图选项

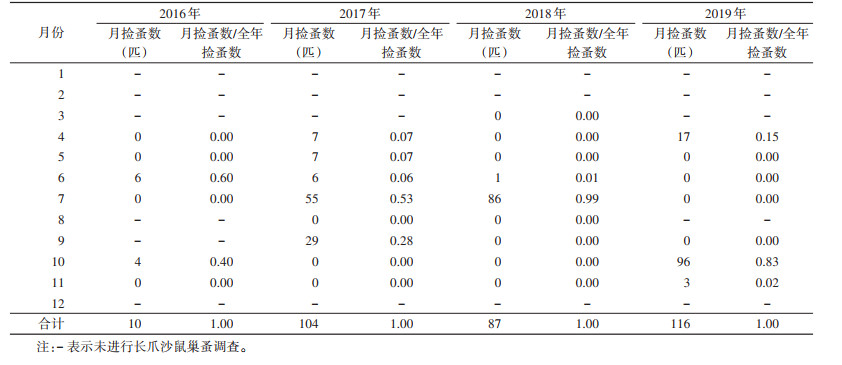
根据表 3数据，2016-2019年长爪沙鼠巢蚤数量变化均有较好的时间聚集性，其中2016年M=0.53，2017年M=0.59，均介于0.5~0.7之间；2018年M=0.98，> 0.9；2019年M值=0.72，介于0.7~0.9之间。

表 3 2016-2019年河北省鼠疫自然疫源地长爪沙鼠巢蚤数量统计 Table 3 Numbers of Meriones unguiculatus nest fleas in a natural plague focus of Hebei province, 2016-2019

表选项

根据表 4数据，2016年(r=0.524，Z=0.914，P > 0.05)不存在角均数，即没有一个平均方向。2017年(r=0.754，Z=19.690，P < 0.001)、2018年(r=0.995，Z=6.806，P < 0.001)和2019年(r=0.996，Z=25.121，P < 0.001)均存在角均数，且分别存在一个平均方向。对2017-2019年角均数进行假设检验，F=3 714.353，P < 0.05，3个样本的角均数不在同一个总体角均数。进行两两比较，2017和2018年(F=120.917，P < 0.05)、2018和2019年(F=6 768.255，P < 0.05)存在角均数，2017和2019年(F=-94.894，P > 0.05)不存在角均数。故2017和2019年的角均数是同一个总体角均数，数据合并(r=0.535，Z=21.007，P < 0.001)存在平均角，a=115.76°，增长的高峰时点为4月27-28日。根据平均角95%可信区间a±1.96S_a和S_a=57.295 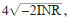，估计增长高峰期为2月20日至7月1日。

表 4 2016-2019年河北省鼠疫自然疫源地长爪沙鼠巢蚤数量增长平均角计算结果 Table 4 Calculation of the mean angle of the population growth of the nest fleas of Mongolian gerbils in a natural plague focus of Hebei province, 2016-2019

表选项

2018年(r=0.995，Z=6.806，P < 0.001)存在平均角，a=167.24°，增长的高峰时点为6月18-19日。根据平均角95%可信区间a±1.96S_a和S_a=57.295 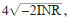，估计增长高峰为6月8-30日。

向量合成表示法—集中度综合全年各月的情况，能够比较真实地反映某种疾病在全年内的集中程度，其结果不受样本量的影响，该方法虽粗略，但判定的结果比较符合实际。主要用于疾病流行规律^[4]或时间聚集性的分析^[9]。

在医学上，经常有表示在一个圆周上位置的记录，称为圆分布资料，这种记录仅表示位置，不存在数量上的大小、质量高低等的差异，只是圆周上所占位置的不同。圆分布统计广泛用于时间数据、日期数据及其他角资料的分析。如用于疾病发病规律^[7]、媒介生物的季节消长^[8]、流行病季节分布^[10]、出生缺陷^[11]及汛期分期^[12]等研究中。其不仅可以分析传染病发病季节性，即集中趋势，亦可准确计算发病高峰时点和高峰期。圆形分布法适用于单峰的圆分布数据，不适用于分析分散的发病数据，适用于有明显集中趋势的数据，使用时可用Rayleigh’s检验进行均衡性检验。圆形分布通过对趋势性、季节性和一定周期规律资料的分析，能够得到较为实际的预测效果。

本文对2016-2019年河北省长爪沙鼠鼠疫自然疫源地长爪沙鼠巢蚤数量的季节性进行分析，集中度法发现长爪沙鼠巢蚤数量变化均有较好的时间聚集性，但各个年份聚集性强度有所不同，其中以2018和2019年季节性最强。此结论与圆形分布法研究结果基本一致。2017和2019年季节性分布一致，与2018年的高峰期重合，但高峰时点不同，可能受多方面因素影响。如2017年10月河北省长爪沙鼠鼠疫自然疫源地再次暴发动物间疫情，此后进行了大规模的灭鼠工作，2018年年初仍进行了相当规模的灭鼠工作可能是直接导致该年巢蚤数量高峰时点延迟出现的原因。

本研究结果与刘纪有^[13]和刘满福等^[14]的研究结果基本一致。既往采用季节消长曲线虽能够反映蚤类的季节变化规律，但缺乏量化的统计分析，且受样本量及采集时间的影响较大，而集中度法和圆形分布法均可以较为科学地进行统计分析，且不受样本量及采集时间的影响，二者均较好地反映一个周期内各个时间点的影响。集中度根据全年各月的情况计算获得，能真实反映疾病发病的季节性分布，且不受数据分布影响，而圆形分布法可计算出疾病的发病高峰时点和高峰期，但仅适用于单峰型分布数据，故建议用集中度对资料的季节性进行探讨，用圆形分布法探索发现蚤类的季节增长高峰时点和高峰期，将二者结合应用于蚤类数量季节性研究。巢蚤较体蚤更能客观反映蚤类数量变化，掌握鼠疫疫源地巢蚤数量季节性变化规律对科学、合理地制定和调整鼠疫防治策略和措施具有一定的参考价值，笔者希望通过后续研究能够弥补巢蚤研究的连续性和规范性。

利益冲突  无