扩展功能
文章信息
- 周毅彬, 朱江, 冷培恩, 吴寰宇
- ZHOU Yi-bin, ZHU Jiang, LENG Pei-en, WU Huan-yu
- 基于泰勒幂法则的诱蚊灯抽样模型研究
- A study of mosquito lamp sampling model based on Taylor's power law
- 中国媒介生物学及控制杂志, 2021, 32(1): 21-25
- Chin J Vector Biol & Control, 2021, 32(1): 21-25
- 10.11853/j.issn.1003.8280.2021.01.003
-
文章历史
- 收稿日期: 2020-07-30
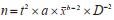 的抽样模型,计算在95%可信区间(95%CI)条件下,上海市淡色库蚊和白纹伊蚊种群开展诱蚊灯密度监测或调查研究所需的抽样单元数。结果 淡色库蚊的泰勒幂方程拟合结果:a=5.847 8,b=1.525 4,R2=0.911 1(P < 0.001);白纹伊蚊泰勒幂方程拟合结果:a=3.668 2,b=1.302 6,R2=0.962 0(P < 0.001)。拟合结果与t分布概率值及相对精度D值组合,构成抽样模型。结果显示,在2019年5月上旬至11月中旬间,95%CI条件下,除4月上旬和下旬外,其余时间淡色库蚊的抽样相对精度D值均 < 0.35,其中5月下旬至8月下旬均 < 0.25;7月上旬至10月上旬,以及10月下旬白纹伊蚊抽样相对精度D值在0.25~0.35之间,其余时间D值均>0.35。结论 该抽样模型具备实用意义,可以据此估算诱蚊灯监测的最佳样本含量。目前上海市的CO2诱蚊灯监测方法,淡色库蚊的相对精度高于白纹伊蚊,若要提高白纹伊蚊抽样相对精度需增加诱蚊灯数量。
的抽样模型,计算在95%可信区间(95%CI)条件下,上海市淡色库蚊和白纹伊蚊种群开展诱蚊灯密度监测或调查研究所需的抽样单元数。结果 淡色库蚊的泰勒幂方程拟合结果:a=5.847 8,b=1.525 4,R2=0.911 1(P < 0.001);白纹伊蚊泰勒幂方程拟合结果:a=3.668 2,b=1.302 6,R2=0.962 0(P < 0.001)。拟合结果与t分布概率值及相对精度D值组合,构成抽样模型。结果显示,在2019年5月上旬至11月中旬间,95%CI条件下,除4月上旬和下旬外,其余时间淡色库蚊的抽样相对精度D值均 < 0.35,其中5月下旬至8月下旬均 < 0.25;7月上旬至10月上旬,以及10月下旬白纹伊蚊抽样相对精度D值在0.25~0.35之间,其余时间D值均>0.35。结论 该抽样模型具备实用意义,可以据此估算诱蚊灯监测的最佳样本含量。目前上海市的CO2诱蚊灯监测方法,淡色库蚊的相对精度高于白纹伊蚊,若要提高白纹伊蚊抽样相对精度需增加诱蚊灯数量。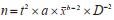 . The number of sample units needed for Cx. pipiens pallens and Ae. albopictus density surveillance was calculated at the 95% confidence level according to the sampling model. Results The fitting results of Taylor's power equation were as follows:a=5.847 8, b=1.525 4, and R2=0.911 1 (P < 0.001) for Cx. pipiens pallens; and a=3.668 2, b=1.302 6, and R2=0.962 0 (P < 0.001) for Ae. albopictus. The fitting results were entered into the sampling model, along with the value of t distribution and the D value of relative precision. The D value at the 95% confidence level for Cx. pipiens pallens was < 0.35 during the middle ten days of April and during the first ten days of May to the middle ten days of November, and was < 0.25 during the last ten days of May to the last ten days of August. The D value for Ae. albopictus was between 0.25 and 0.35 from the first ten days of July to the first ten days of October and during the last ten days of October, and was >0.35 during other periods. Conclusion This sampling model has practical significance and can be used to estimate the optimal sample size for light trap monitoring. The current mosquito surveillance method by carbon dioxide trapping lamps in Shanghai shows higher relative precision for Cx. pipiens pallens than Ae. albopictus. The relative precision for Ae. albopictus can be improved by increasing the number of light traps.
. The number of sample units needed for Cx. pipiens pallens and Ae. albopictus density surveillance was calculated at the 95% confidence level according to the sampling model. Results The fitting results of Taylor's power equation were as follows:a=5.847 8, b=1.525 4, and R2=0.911 1 (P < 0.001) for Cx. pipiens pallens; and a=3.668 2, b=1.302 6, and R2=0.962 0 (P < 0.001) for Ae. albopictus. The fitting results were entered into the sampling model, along with the value of t distribution and the D value of relative precision. The D value at the 95% confidence level for Cx. pipiens pallens was < 0.35 during the middle ten days of April and during the first ten days of May to the middle ten days of November, and was < 0.25 during the last ten days of May to the last ten days of August. The D value for Ae. albopictus was between 0.25 and 0.35 from the first ten days of July to the first ten days of October and during the last ten days of October, and was >0.35 during other periods. Conclusion This sampling model has practical significance and can be used to estimate the optimal sample size for light trap monitoring. The current mosquito surveillance method by carbon dioxide trapping lamps in Shanghai shows higher relative precision for Cx. pipiens pallens than Ae. albopictus. The relative precision for Ae. albopictus can be improved by increasing the number of light traps.蚊媒传染病是我国主要的传染病之一[1]。阻断蚊媒传染病传播,遏制其流行的重要途径为对其媒介蚊虫的监测和控制[2]。目前全国最常用的蚊虫监测方法之一为诱蚊灯法[3]。诱蚊灯是基于蚊虫的趋光性,在蚊虫靠近时利用风扇形成的负压将其吸入集蚊袋的设备。诱蚊灯法监测蚊虫密度具有操作简便、监测结果相对客观和可多位点同时开展监测等优点[4]。目前我国的诱蚊灯法监测中,未发现关于样本量和抽样误差的研究,因此我们基于泰勒幂法则(Taylor’s power law)建立诱蚊灯抽样模型。泰勒幂法则是1961-1965年Taylor等[5-7]在研究生物种群时,发现许多物种的种群密度的方差(s2)与均值(x)之间存在显著的幂函数关系,许多学者运用泰勒幂法则进行了多项生态学方面的研究[8-10]。
本研究将泰勒幂法则代入抽样公式,进而建立上海市主要蚊种白纹伊蚊(Aedes albopictus)和淡色库蚊(Culex pipiens pallens)的诱蚊灯法密度监测的抽样模型,估算抽样相对精度和最佳样本含量。
1 材料与方法 1.1 诱蚊灯法蚊密度监测在上海全市16个区中的15个区(除崇明区三岛)共设置229个CO2诱蚊灯监测点。各区选择医院、农户、牲畜棚(如有则选择牛棚、猪圈、羊圈或养殖场等)各2处作为监测点,其余按照城镇居民区、公园(含街心公园)、学校等场所平均分配。除牲畜棚外,其余监测点在外环境进行,每个监测点设置1个CO2诱蚊灯。于2019年4-11月每旬监测1次,监测时间为16:00-22:00,遇雨天、风力大于5级顺延1 d开展监测。捕获的蚊虫收集至实验室,在体视镜下分类鉴定并计数。
诱蚊灯法密度计算公式:
蚊密度〔只/(灯·夜)〕=捕获雌蚊数(只)/〔布放灯数(灯)×诱蚊夜数(夜)〕
本次选用的CO2诱蚊灯具有三重引诱方式:CO2气体(4 L气瓶)、光源和诱饵,由上海禾奇科学仪器有限公司生产。
1.2 回归分析、泰勒幂方程及抽样模型

|
(1) |
其中,a、b为2个非负参数,a是与抽样等因素有关的参数,b是反映物种聚集特征的参数,由物种的生物学行为与环境因素之间的相互作用决定,不受环境异质性的影响,被称为泰勒幂指数[11]。泰勒幂指数不受样本方差和计算方法的影响,若b > 1,种群空间格局为聚集型;b=1为随机型;b < 1为均匀型。
将(1)式泰勒幂法则方程,等式两边取对数得:
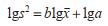
|
(2) |
计算每旬监测的229个CO2诱蚊灯样本的蚊虫密度x和s2,分别转换为对数值lgx和lgs2。根据公式(2)建立线性回归分析,计算b和lga的值,再将直线回归式反转,转化为相应的幂函数方程(1),得到a和b的值。
所采用的样本含量估算公式:
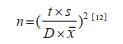
|
(3) |
式中,n值是调查所需的样本含量,t值取自t分布表〔取95%可信区间(CI)条件〕,D值为相对精度,s值和x值是目标蚊种密度的标准差和平均密度。式中的t和D可被认为是常数,而s和x则是统计量。
然后将(1)式带入(3)式得:
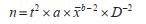
|
(4) |
由此模型估算诱蚊灯在相应取样条件下的目标蚊种最佳样本含量。
1.3 统计学分析采用Excel 2007软件进行数据录入和整理,SPSS 20.0软件进行统计分析。检验水准取α=0.05。
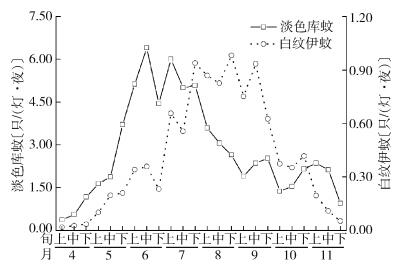
2 结果 2.1 诱蚊灯捕获蚊虫情况2019年4月上旬至11月下旬间,229个CO2诱蚊灯共捕获淡色库蚊18 267只,其中雌蚊15 610只,占该蚊总数的85.45%;捕获白纹伊蚊2 758只,其中雌蚊2 335只,占该蚊总数的84.66%,淡色库蚊和白纹伊蚊密度的季节变化见图 1。上海市淡色库蚊在5月下旬至8月上旬出现密度高峰,白纹伊蚊于7月上旬至9月下旬出现密度高峰,两者在10月中下旬都出现1个次高峰,11月后密度逐步下降。
|
| 图 1 上海市2019年4-11月淡色库蚊和白纹伊蚊密度的季节变化 Figure 1 Seasonal variations in densities of Culex pipiens pallens and Aedes albopictus in Shanghai from April to November 2019 |
| |
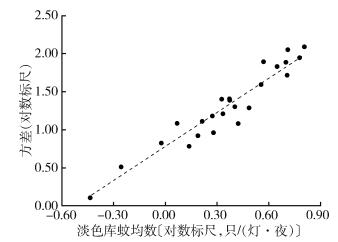
计算229个CO2诱蚊灯每旬监测的淡色库蚊和白纹伊蚊密度的x和s2,分别转换为其对数值lgx和lgs2。根据公式(2)线性回归分析,计算b和lga,结果见图 2、3,拟合参数结果见表 1。淡色库蚊泰勒幂法则方程拟合结果:a=5.847 8,b=1.525 4,R2 = 0.911 1(P < 0.001);白纹伊蚊泰勒幂方程拟合结果a=3.668 2,b=1.302 6,R2 =0.962 0(P < 0.001)。两者拟合后的R2均 > 0.900 0,拟合优度较好,且大多数观察点在回归直线附近,适合采用泰勒幂法则。此外淡色库蚊和白纹伊蚊的泰勒幂方程拟合均表现为泰勒幂指数b > 1,显示两者的种群空间分布格局都为聚集型分布。
|
| 图 2 上海市淡色库蚊密度样本方差与均数的幂函数回归 Figure 2 Power regression of variances and means of densities of Culex pipiens pallens samples in Shanghai |
| |
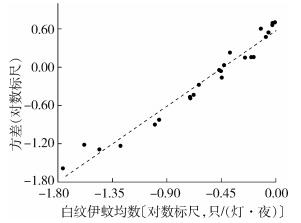
|
| 图 3 上海市白纹伊蚊密度样本方差与均数的幂函数回归 Figure 3 Power regression of variances and means of densities of Aedes albopictus samples in Shanghai |
| |

|
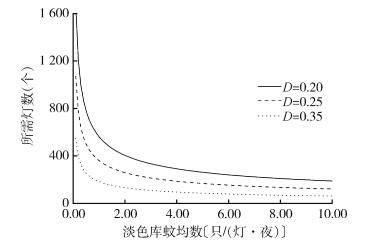
分别将计算所得淡色库蚊和白纹伊蚊密度的泰勒幂法则的a和b值代入公式(4),估算其最佳样本含量。取t=1.96(95%CI条件下),D=0.20、0.25或0.35(3个不同的相对精度水平)。应用抽样模型计算所得不同密度均数水平下的n值就是所需诱蚊灯的样本单元数(图 4、5)。结果显示,当淡色库蚊和白纹伊蚊平均密度较低且D值较小(相对精度较高)时,必须放置较多的样本单元数量(诱蚊灯数量);反之,当平均蚊密度较高且D值较大(相对精度较低)时,放置较少的诱蚊灯即可满足需要。同时,在95%CI条件下,这些曲线推荐了上海市今后针对淡色库蚊和白纹伊蚊种群开展该诱蚊灯密度调查研究所需的抽样单元数。
|
| 注:D为相对精度。 图 4 上海市诱蚊灯监测淡色库蚊在不同相对精度下的最佳样本含量 Figure 4 The optimal sample size at different relative precision values for Culex pipiens pallens surveillance by light traps in Shanghai |
| |
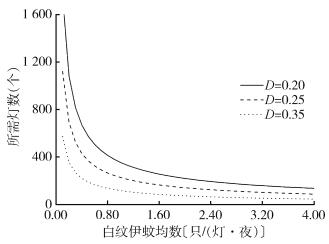
|
| 注:D为相对精度。 图 5 上海市诱蚊灯监测白纹伊蚊在不同相对精度下的最佳样本含量 Figure 5 The optimal sample size at different relative precision values for Aedes albopictus surveillance by light traps in Shanghai |
| |
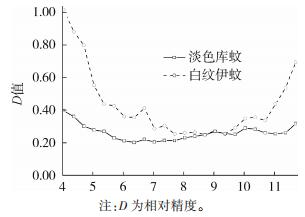
2019年4月上旬至11月下旬诱蚊灯法监测淡色库蚊和白纹伊蚊密度,95%CI条件下,所对应的抽样D值变化见图 6。除4月上旬和下旬外,其余时间淡色库蚊所对应的抽样D值均 < 0.35,5月下旬至8月下旬均 < 0.25;7月上旬至10月上旬,以及10月下旬白纹伊蚊D值在0.25~0.35之间,其余时间D值均 > 0.35。
|
| 注:D为相对精度。 图 6 上海市2019年诱蚊灯法淡色库蚊和白纹伊蚊密度监测相对精度的变化 Figure 6 Changes in relative precision for Culex pipiens pallens and Aedes albopictus surveillance by light traps in Shanghai, 2019 |
| |
在开展媒介生物调查和监测中,重要的是决定样本含量等方面的信息,以使种群密度的估计能够达到一个预先给定的精确度水准和抽样效率上的平衡。在精确度确定之后,调查的样本规模过大则造成浪费;调查的样本规模过少,则精确度过低,可信度差,不足以准确掌握被调查种群的密度。为此我们将关于生物种群方差和均数间关系的泰勒幂法则用于抽样设计。泰勒幂法则可揭示物种种群大小、密度方差与均值的规律特征,也可用于样本量的估计[13]。泰勒幂法则中的参数b是种群行为特征的反映,是种群的特征参数。本次上海市淡色库蚊和白纹伊蚊的泰勒幂法则方程拟合,均表现为b > 1,显示这2个种群在上海市的空间分布格局均为聚集型分布。
本研究将泰勒幂法则拟合的参数代入样本量公式得到: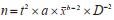
泰勒幂法则用于样本量计算的公式同时可以评估不同样本量在监测中的抽样精确性。D值约为抽样误差的一半,可被用来表示种群的抽样精确度,D值越小抽样精确度越高;反之则越低。上海市共设置229个CO2诱蚊灯,在95%CI条件下,淡色库蚊在密度 > 2.90只/(灯·夜)时,相对精度D < 0.25,当密度 > 0.80只/(灯·夜)时,D < 0.35;白纹伊蚊在密度 > 1.10只/(灯·夜)时,D < 0.25,当密度 > 0.50只/(灯·夜)时,D < 0.35。目前上海市诱蚊灯监测设置的229个监测点,对于淡色库蚊在绝大多数时间其抽样的D值均在0.35水平以上,但是白纹伊蚊仅在高峰季节抽样的D值能达到该水平。如需增加白纹伊蚊密度监测D值则需要增加诱蚊灯的设置数量。
本研究基于上海市诱蚊灯监测的全市平均蚊密度,验证了此模型的使用价值。但是未考虑诱蚊灯在不同生境的设置,在下一步研究中将增加不同生境的单独统计,对比研究结果为确定诱蚊灯在不同生境设置的数量提供理论依据。
本研究基于泰勒幂法则建立的抽样模型具有实用意义,可以据此估算诱蚊灯监测的最佳样本含量。目前上海市的诱蚊灯监测方法,淡色库蚊的相对精度高于白纹伊蚊,若要提高白纹伊蚊监测相对精度需增加诱蚊灯数量。此外,针对白纹伊蚊监测寻找更为敏感的监测工具也可能是改变目前监测的样本量情况下相对精度较低的方法,此模型也可为挑选合适的监测工具或方法时提供依据。
利益冲突 无
| [1] |
王亚丽, 王煊, 任瑞琦, 等. 中国2013-2016年境外输入传染病的流行病学特征[J]. 中华流行病学杂志, 2017, 38(11): 1499-1503. Wang YL, Wang X, Ren RQ, et al. Epidemiology of imported infectious diseases in China, 2013-2016[J]. Chin J Epidemiol, 2017, 38(11): 1499-1503. DOI:10.3760/cma.j.issn.0254-6450.2017.11.012 |
| [2] |
闫冬明, 黄坤, 赵春春, 等. 常用蚊虫监测方法和技术研究进展[J]. 中国媒介生物学及控制杂志, 2020, 31(1): 108-112. Yan DM, Huang K, Zhao CC, et al. Research advances in common methods and techniques for mosquito surveillance[J]. Chin J Vector Biol Control, 2020, 31(1): 108-112. DOI:10.11853/j.issn.1003.8280.2020.01.023 |
| [3] |
郭玉红, 吴海霞, 刘小波, 等. 2018年全国媒介蚊虫监测报告[J]. 中国媒介生物学及控制杂志, 2019, 30(2): 128-133. Guo YH, Wu HX, Liu XB, et al. National vectors surveillance report on mosquitoes in China, 2018[J]. Chin J Vector Biol Control, 2019, 30(2): 128-133. DOI:10.11853/j.issn.1003.8280.2019.02.003 |
| [4] |
郭玉红, 刘京利, 鲁亮, 等. 诱蚊灯法与人工小时法捕蚊效果比较研究[J]. 中国媒介生物学及控制杂志, 2012, 23(6): 529-532. Guo YH, Liu JL, Lu L, et al. Comparative study on mosquito-trapping effects of lamp trapping method and labor hour method[J]. Chin J Vector Biol Control, 2012, 23(6): 529-532. |
| [5] |
Taylor LR. A natural law for the spatial disposition of insects[C]//Paul F. Proceedings of the 12th international congress of entomology, 1964. London: Royal Entomological Society of London, 1964: 396-397.
|
| [6] |
Taylor LR. Assessing and interpreting the spatial distributions of insect populations[J]. Annu Rev Entomol, 1984, 29: 321-357. DOI:10.1146/annurev.en.29.010184.001541 |
| [7] |
Taylor RAJ, Lindquist RK, Shipp JL. Variation and consistency in spatial distribution as measured by Taylor's Power Law[J]. Environ Entomol, 1998, 27(2): 191-201. DOI:10.1093/ee/27.2.191 |
| [8] |
王平, 李芳, 杨清培, 等. 基于Ripley's K函数和Taylor幂法则的江西省豚草种群空间分布的点格局分析[J]. 植物保护学报, 2019, 46(1): 130-135. Wang P, Li F, Yang QP, et al. Point pattern analysis of spatial distribution of ragweed population in Jiangxi province based on Ripley's K function and Taylor's power law[J]. J Plant Prot, 2019, 46(1): 130-135. DOI:10.13802/j.cnki.zwbhxb.2019.2019916 |
| [9] |
廖为财, 何万存. 棉蚜在棉田的空间分布型研究[J]. 江西植保, 2010, 33(3): 124-126. Liao WC, He WC. Spacial distribution of Aphis gossypii glover in cotton fields[J]. Jiangxi Plant Protect, 2010, 33(3): 124-126. DOI:10.3969/j.issn.2095-3704.2010.03.011 |
| [10] |
雷蕾, 郑嘉. 泰勒幂法则对中国人口死亡率的检验[J]. 中央民族大学学报:自然科学版, 2018, 27(2): 83-89. Lei L, Zheng J. Taylor's law tests on China's population mortality[J]. J MUC:Nat Sci Ed, 2018, 27(2): 83-89. DOI:10.3969/j.issn.1005-8036.2018.02.014 |
| [11] |
Shi PJ, Sandhu HS, Reddy GVP. Dispersal distance determines the exponent of the spatial Taylor's power law[J]. Ecol Modell, 2016, 335: 48-53. DOI:10.1016/j.ecolmodel.2016.05.008 |
| [12] |
Southwood TRE, Henderson PA. Ecological methods[M]. 3rd ed. Oxford: Blackwell Science, 2000: 21.
|
| [13] |
Zhou GF, Minakawa N, Githeko A, et al. Spatial distribution patterns of malaria vectors and sample size determination in spatially heterogeneous environments:a case study in the West Kenyan Highland[J]. J Med Entomol, 2004, 41(6): 1001-1009. DOI:10.1603/0022-2585-41.6.1001 |
| [14] |
Williams CR, Long SA, Webb CE, et al. Aedes aegypti population sampling using BG-sentinel traps in North Queensland Australia:statistical considerations for trap deployment and sampling strategy[J]. J Med Entomol, 2007, 44(2): 345-350. DOI:10.1093/jmedent/44.2.345 |
 2021, Vol. 32
2021, Vol. 32

