肾综合征出血热(HFRS)是由汉坦病毒引起的与啮齿动物相关的人兽共患病。HFRS于20世纪30年代初在中国东北地区被发现，自此全国范围内每年均有HFRS病例报告^[1]。我国HFRS占全球HFRS总数的90%以上，根据原国家卫生和计划生育委员会的统计数据，1950-2014年期间，我国共报告HFRS 1 625 002例病例和46 968例死亡病例，病死率为2.89%^[2]。自1955年以来，辽宁省一直是我国受HFRS影响最严重的地区之一，2004年发病率为13.05/10万，居全国首位^[3]。其中沈阳市HFRS疫情范围不断蔓延，严重危害公众健康。利用微分动力学方程模拟HFRS传播动力学，预测HFRS发病趋势，有望为制定预防控制措施提供依据。微分动力学方程通过参数化传染病传播特征，讨论影响感染传播的影响因素，进而预测人群水平的流行动态；通过在方程中将针对传染病控制措施参数化，帮助优化资源的使用。目前微分动力学方程已经广泛应用于传染病疫情预测与防控中^[4-6]；本研究利用沈阳市HFRS发病数据，建立动力学模型预测沈阳市发病趋势，论证该模型用于探讨有效防控措施的可能性。

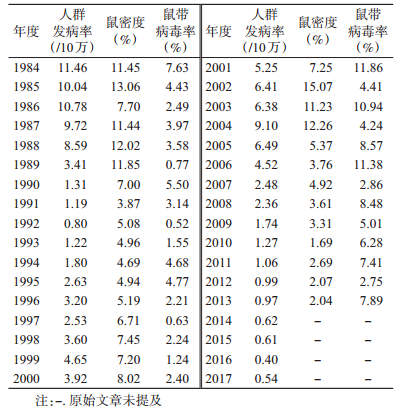
收集已公开发表的辽宁省沈阳市1984-2017年HFRS人群发病数据、1984-2013年鼠密度和鼠带病毒率数据^[7-9](表 1)。其中数据收集标准参照原卫生部颁发的《全国肾综合征出血热监测方案(试行)》。1984-2017年沈阳市人群HFRS年平均发病率为3.88/10万；1984-2013年沈阳市年平均鼠密度为6.93%，鼠带病毒率为4.79%。

表 1 1984-2017年沈阳市人群HFRS发病率、鼠密度及鼠带病毒率 Table 1 The incidence rates of hemorrhagic fever with renal syndrome in humans, density of rodents, and virus-carrying rates among rodents in Shenyang, 1984-2017

表选项

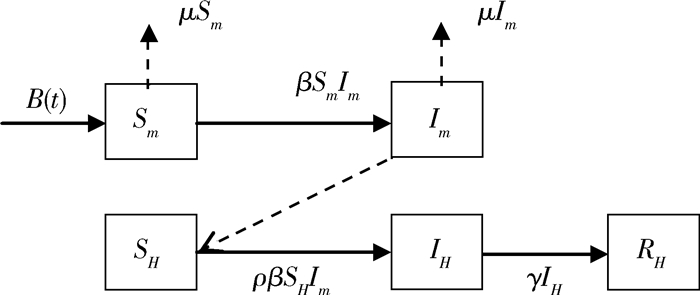
HFRS动力学模型描述见图 1，鼠类群体分为易感鼠(S_m)与带病毒鼠(I_m)，用S_m和I_m分别表示t时刻易感鼠和带病毒鼠所占的比例，S_m+I_m＝1；人群中不考虑人口出生、死亡和迁移，分为易感者(S_H)、感染者(I_H)和恢复者(R_H)，S_H、I_H、R_H分别为易感者、感染者、恢复者在t时刻时占人群总数的比例，S_H+I_H+R_H＝1。根据HFRS流行病学特征，模型中假定易感个体通过直接接触病毒感染进入感染状态，恢复后获得终身免疫。

注:Sm、Im分别代表易感鼠和带病毒鼠所占的比例，SH、IH、RH分别代表易感者、感染者和恢复者占人群总数的比例；B(t)为t时刻鼠类出生率，易感鼠(Sm)以βSmIm的速度被感染为带病毒鼠(Im)，μSm和μIm分别代表易感鼠和带病毒鼠中自然死亡的比例；易感人群(SH)以ρβSHIm速率受带病毒鼠(Im)传染为感染者(IH)，并以γIH恢复为恢复者(RH) 图 1 沈阳市鼠间、人间HFRS传播动力学的描述 Figure 1 Kinetics of rat-to-rat and rat-to-human transmission of hemorrhagic fever with renal syndrome in Shenyang

图选项

鼠类繁殖季节变化以及环境承载力是造成啮齿动物种群密度变化的原因^[10-11]。

B(t)随时间变化的函数表达式^[10-11]如下:

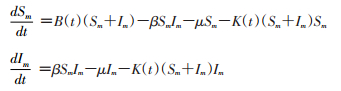
出生率的计算考虑到1年内鼠类繁殖动力变化，1年内有6个月的繁殖季，另外6个月(10月至翌年3月)内出生率为0^[10-11]。K(t)是环境承载力，考虑到密度依赖效应以及季节变化对死亡率的影响，函数表达式^[10-11]如下:

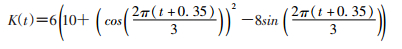
人群内患HFRS动力学表达式如下:

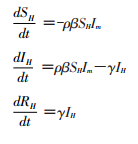
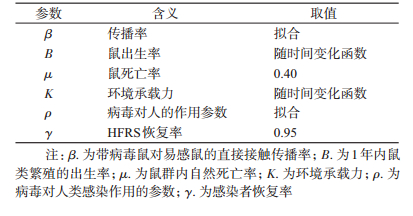
式中，β为带病毒鼠对易感鼠的直接接触传播率，μ为鼠群内自然死亡率，ρ代表病毒对人类感染作用的参数，ρβ代表带病毒鼠对易感人群的直接接触传播率，γ代表感染者恢复率。模型内参数解释见表 2。

表 2 利用微分动力学模拟人间HFRS发病率动力学变化传染病模型内参数含义及取值 Table 2 Meanings and values of parameters in the differential kinetic model to simulate the dynamics of the incidence of hemorrhagic fever with renal syndrome in humans

表选项

将1984-2017年沈阳市HFRS发病率数据分成训练集(1984-2004年数据)和验证集(2005-2017年数据)，使用训练集数据训练模型并使用Matlab 2017软件拟合参数β和ρ。辽宁省于2005年开始对16~60岁易感人群进行大规模免疫预防接种HFRS疫苗^[12]，在后续模型验证中引入参数v(v表示疫苗的覆盖范围)，假定疫苗覆盖范围平均值为40.00%的β分布，疫苗对易感人群的保护率为90.00%，根据辽宁省统计年鉴，沈阳市16~60岁人口数约占总人口数的65.00%，2005年之后易感人群动力学模型如下:

对模型重复模拟1 000次，模拟出2006-2017年发病率的90%置信区间，与实际发病率数据比较，采用误差绝对值来检验模型预测效果；上述模型的构建基于Matlab 2017软件来实现。

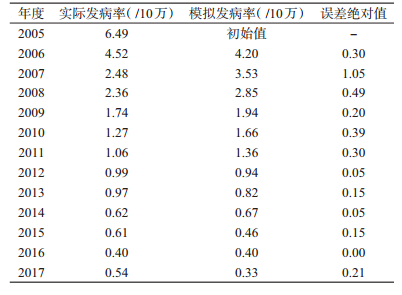
通过Matlab 2017软件拟合出β与ρ值分别为0.704和0.000 06，以沈阳市2005年HFRS发病率数据为初始值模拟2005-2017年沈阳地区HFRS发病率，预测结果见表 3，微分动力学方程预测发病率与实际发病率比较(图 2)，平均误差绝对值为0.28。

表 3 2005-2017年沈阳市HFRS实际发病率、动力学模型预测值与误差绝对值 Table 3 Actual incidence of hemorrhagic fever with renal syndrome, model predicted incidence of hemorrhagic fever with renal syndrome, and absolute error in Shenyang, 2005-2017

表选项

图 2 利用微分动力学模型模拟沈阳市2005-2017年人间HFRS发病率90%置信区间与实际发病率情况 Figure 2 Simulated incidence of hemorrhagic fever with renal syndrome at a 90% confidence interval using a differential kinetic model and actual incidence in Shenyang, 2005-2017

图选项

在模型中提高v参数，将疫苗覆盖范围从40.00%扩大至平均值为50.00%的β分布范围，2005-2017各年HFRS发病率均降低，且下降速率加快(表 4)，扩大免疫范围后模拟发病率与实际发病率比较见图 3，2005-2017年沈阳市人群HFRS平均发病率将从1.97/10万下降至1.91/10万。

表 4 疫苗覆盖范围从40%扩大至50%时2005-2017年沈阳市HFRS模拟发病率(/10万) Table 4 Simulated incidence of hemorrhagic fever with renal syndrome (/100 000) with the vaccination coverage expansion from 40% to 50% in Shenyang, 2005-2017

表选项

图 3 利用微分动力学模型模拟2005-2017年在扩大免疫范围后人间HFRS发病率与实际发病率情况 Figure 3 Simulated incidence of hemorrhagic fever with renal syndrome in humans using a differential kinetic model and actual incidence after expansion of vaccination coverage, 2005-2017

图选项

人畜共患病日益威胁人类健康，传染病模型能够分析病原体在动物宿主内传播动态以及对人群的影响。HFRS在我国发病率高、发病例数多，是我国严重的公共卫生问题之一。通过微分动力学方程得出，疫苗免疫是控制人间HFRS疫情的有效防控措施，扩大疫苗免疫覆盖范围可以有效保护易感人群。基于数学模型预测发病率情况是控制HFRS疫情、优化预防措施的有效途径。目前用于预测HFRS发病率的数学模型包括自回归移动平均-广义回归神经网络(ARIMA-GRNN)模型、反向传播(BP)神经网络模型和灰色模型等^[13-14]，上述模型的优点是预测结果准确、所需样本量小以及计算简便，但HFRS作为动物疫源性疾病，动物的感染情况直接影响到人群的发病风险，因此本研究在动物和人群中分别建立SI、SIR传染病模型，以得出人群HFRS发病趋势受动物群体影响的规律。

本研究中的微分动力学模型纳入疫苗参数、小鼠出生率变化函数和环境承载力函数模拟沈阳市HFRS人间发病率变化。模型模拟结果显示出与实际发病率相同趋势，平均误差绝对值为0.28。模型提示，如果扩大疫苗免疫范围，人间HFRS发病率下降速度将变快，证明疫苗免疫是有效的预防控制措施，提示未来应对16~60岁的易感人群加强免疫以实现对HFRS的有效防控。有研究表明，啮齿群体中环境承载力是影响HFRS人群发病率的重要因素^[15]，空间与时间性的环境因素影响着环境承载力和啮齿类动物出生率^[16]，未来的工作将在模型中纳入季节性参数以更准确模拟人群中HFRS发病规律。本研究将及时更新沈阳市HFRS疫情数据、鼠带病毒率、鼠密度和免疫接种范围等数据，动态评估该微分动力学模型的适用范围和有效性，希望能为完善HFRS预警系统提供一定的方法学储备。