白纹伊蚊（Aedes albopictus）在我国分布广泛，除扰人吸血外，还作为媒介传播登革热、基孔肯雅热、寨卡病毒病等多种蚊媒传染病，由于缺乏有效疫苗预防和特异药物治疗，白纹伊蚊密度监测与消杀是控制该类疾病的最有效方法。对白纹伊蚊密度进行监测，可以为登革热等疾病的风险评估、预测预警、防控提供参考依据^[1]，具有重要的公共卫生意义。目前白纹伊蚊密度监测仍以幼蚊监测方法为主，主要有布雷图指数法、诱蚊诱卵器法、标准间指数法等^[2]，上海市松江区从2014年开始设立白纹伊蚊密度监测点，运用诱蚊诱卵器法监测白纹伊蚊密度，监测点已经覆盖到全区15个街道（镇），白纹伊蚊密度呈现一定的季节性和周期性。为此我们利用2014－2018年4－11月松江区白纹伊蚊诱蚊诱卵器监测数据，应用移动平均法的季节趋势模型对松江区2019年4－11月的白纹伊蚊诱蚊诱卵器指数（MOI）进行预测分析，为登革热等蚊媒传染病的预警和防制提供参考依据。

白纹伊蚊密度选用松江区2014－2018年4－11月每月监测得到的MOI数据。

参考《登革热防治技术指南》[中疾控传防发（2014）360号]中的《媒介伊蚊监测指南》采用诱蚊诱卵器法进行监测。于4－11月每月中旬开展1次。每个监测点共放置不少于50只诱蚊诱卵器，主要布放在居民区、单位、学校等楼顶天台、工地、空中花园或外环境的树木、花草、灌木丛等公共绿化带等，每25~30 m布放诱蚊诱卵器1个，在诱蚊诱卵器中加入10~15 ml的脱氯水，放入圆形滤纸，连续布放4 d，第4天检查，记录回收的有效诱蚊诱卵器数、诱捕到成蚊或蚊卵或伊蚊幼蚊的阳性数，计算MOI。MOI=阳性诱蚊诱卵器数/有效诱蚊诱卵器数×100。

采用Excel 2003对松江区2014－2018年MOI以月为时间序列拟合趋势方程建立预测模型，运用移动平均法对2019年的白纹伊蚊密度变化趋势进行预测。

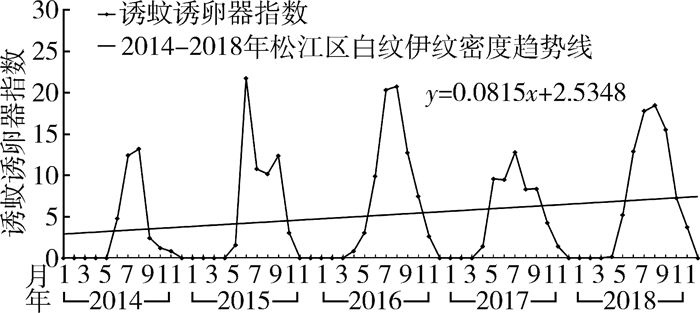
以“月”为时间序列分别统计2014－2018年每月松江区白纹伊蚊MOI，由于模型拟合的要求，松江区未开展监测的1－3、12月诱蚊诱卵器数值暂以0填充。这样以月次（1~60月）为自变量，MOI为因变量拟合线性趋势方程为y=0.081 5x+2.534 8（具体做法：在Excel 2003中作图后，点中图中密度曲线后，右键选择“添加趋势线”选项并显示公式即可），显示松江区白纹伊蚊密度变化呈现明显季节性，每年的6－9月为密度高峰，且密度短期内具有逐年升高的趋势，见图 1。

图 1 2014－2018年松江区白纹伊蚊密度变化情况及趋势 Figure 1 The changes and trend of Aedes albopictus density in Songjiang district, from 2014 to 2018

图选项

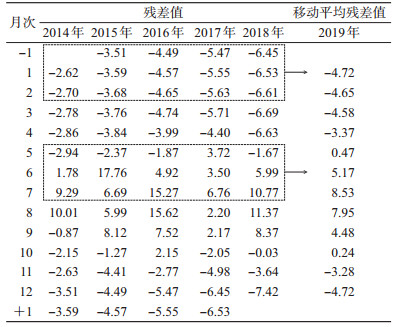
每年按12个月计算，2014－2018年月次排序依次为1~60月，再用每月实际监测的MOI减去按月次代入趋势方程中计算的理论值，得到2014－2018年每月MOI残差值（例如：2018年8月监测的MOI为18.47，而2018年8月对应的排序月次为56，代入y=0.081 5x+2.534 8得到理论的MOI为7.10，故残差为11.37，其他依次类推），再以同期数据前后1个时期的残差值的算术平均值为移动平均值，即为到2019年同期的残差值（移动“窗口”可以根据实际进行调整，本文的“窗口”为5×3=15，如2019年6月移动平均值是用2014－2018年每年5－7月的残差值共15个数据计算平均值，为5.17，其余月次移动平均值依次类推），见表 1。同时计算预测模型的相对误差：相对误差=（趋势值－实际值）/实际值×100%，2014－2018年的平均相对误差为12.82%。

表 1 松江区2014－2018年诱蚊诱卵器指数残差值及2019年残差移动平均值 Table 1 The residual values of mosquito ovitrap index from 2014 to 2018 and the moving average of the residuals in 2019, in Songjiang district

表选项

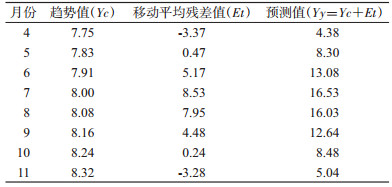
2019年月份接2018年月次排序为61~72月次，代入趋势方程y=0.081 5x+2.534 8，得到2019年1－12月的MOI的理论趋势值（Yc），再分别与2019年1－12月移动平均残差值（Et）相加，即可得到2019年1－12月的每月MOI预测值（Yy）。由于2019年的1－3月及12月MOI预测值，是基于模型拟合的需要，以2014－2018年未开展监测的1－3、12月MOI数值暂以0填充而计算获得，故不能作为参考应舍弃，只保留4－11月的预测值，见表 2。这样与2014－2018年4－11月的MOI整合，依据“MOI≥5有传播风险，≥10有暴发风险，≥20有区域流行风险”伊蚊密度传病风险标准，以5为警戒值，10为预警值，绘制2014－2019年松江区白纹伊蚊密度预警控制图（图 2）。2019年仅4月MOI < 5，5－11月的MOI均 > 5，6－9月的MOI均 > 10，密度高峰在7月，整体上2019年白纹伊蚊密度仍较高。

表 2 移动平均法的季节趋势模型预测松江区2019年白纹伊蚊诱蚊诱卵器指数情况 Table 2 Prediction of mosquito ovitrap index of Aedes albopictus in 2019, in Songjiang district, using the seasonal trend model based on moving average method

表选项

图 2 2014－2018年松江区白纹伊蚊诱蚊诱卵器监测及2019年预测结果 Figure 2 The mosquito ovitrap surveillance results for Aedes albopictus from 2014 to 2018 and the prediction for 2019, in Songjiang district

图选项

白纹伊蚊作为我国登革热的主要传播媒介，密度高低直接影响了登革热发生可能性和流行程度。媒介伊蚊密度监测作为登革热防控工作的首要环节，可以为登革热的风险评估、预测预警、防控效果评估提供数据支持。目前，我国已在媒介伊蚊分布的23个省（自治区、直辖市）按照Ⅰ、Ⅱ、Ⅲ地区划分开展媒介伊蚊监测工作^[1]，其中上海市属于Ⅱ类监测地区，采取的诱蚊诱卵器法在4－11月每月开展1次。利用现有的监测数据，通过合适的方法建立密度预测模型，主动预警，早期了解白纹伊蚊密度变化趋势，及时采取有效防控措施，对指导登革热防控具有重要的现实意义，也是目前研究的重点问题之一。

在卫生研究领域，许多疾病（传染病、慢性非传染性疾病等）受自然、社会、环境等多种因素的影响而呈现出季节性和趋势性变化^[3]。季节趋势模型同时兼顾了趋势性和季节性的影响，能够消除时间序列中的偶然因素对预测结果的影响，突出反映趋势性和周期性的变动，能够得到较为接近实际的预测结果，该模型较多应用在手足口病、甲肝、疟疾、流行性腮腺炎等传染病和医疗机构门诊就诊人次的预测^[4-8]，而在病媒生物监测方面的预测应用很少。本文尝试应用移动平均法的季节趋势模型来预测2019年4－11月松江区白纹伊蚊密度变化情况，拟合计算的2014－2018年的预测值和实际值平均相对误差为12.82%，模型拟合较好，可预测2019年情况。预测结果显示，整体上2019年白纹伊蚊密度仍较高，单峰分布，密度高峰在7月，依据登革热风险评估标准^[1]，2019年的5－11月MOI均 > 5，有传播风险，6－9月的MOI均 > 10，有暴发风险。可根据每月的密度监测值，参考密度预测值提前做出预警，及时作出反应，从2019年5月起便要加强全区的白纹伊蚊密度控制以压制高峰，降低登革热流行风险。

目前，蚊虫密度预测及模型研究较多，包括差分自回归移动平均（ARIMA）模型、灰色多变量灰色模型、神经网络模型等^[9-12]，但这些模型及软件使用均较复杂。季节趋势模型运用计算机计算数据，能充分利用原始数据，方法简便易于掌握、结果直观，具有较高的合理性、可靠性和实用价值^[13]，适合疾病控制和社区平常的媒介监测预测分析使用。需要注意的是，季节趋势模型由于数学模型的导出忽略了不规则变动，仅适用于短期预测^[14]。另外，预测的仅是理论数值，而实际中密度变化受气候、社会及爱国卫生运动等多种因素影响，需要结合实际，判断结果是否适用并及时更新数据拟合方程，使得理论值更加接近实际，以达到更好的预测效果，来更好地指导媒介密度控制工作。