扩展功能
文章信息
- 高文, 黄钢, 韩晓莉
- GAO Wen, HUANG Gang, HAN Xiao-li
- 基于蚊密度差分自回归移动平均模型预测流行性乙型脑炎的贝叶斯判别分析研究
- Application of Bayes analysis in Japanese encephalitis prediction based on multiple seasonal autoregressive integrated moving average model
- 中国媒介生物学及控制杂志, 2018, 29(6): 557-563
- Chin J Vector Biol & Control, 2018, 29(6): 557-563
- 10.11853/j.issn.1003.8280.2018.06.003
-
文章历史
- 收稿日期: 2018-08-02
- 网络出版时间: 2018-10-16 17:28
流行性乙型脑炎(乙脑)是一种由媒介蚊虫传播的严重损害中枢神经系统的人畜共患急性传染病,病死率高[1-2]。多地研究结果显示,蚊密度与乙脑具有季节相关性,蚊密度是影响乙脑发病的重要因素之一[3-4]。
利用时间序列模型可以对病媒生物密度季节消长进行预测[5-6],但该模型的预测值能否反映实际值对虫媒传染病疫情预测预警的研究鲜有报道。本研究利用贝叶斯(Bayes)判别分析方法,从蚊密度监测值和时间序列模型预测值数据出发,将河北省蚊密度监测数据通过使用Bayes分类算法对是否发生乙脑进行预测,对比Bayes判别结果,验证时间序列蚊密度模型与乙脑的关系,探讨差分自回归移动平均(ARIMA)模型预测拟合的河北省蚊密度季节消长模型对乙脑发生的预测预警作用,论证ARIMA模型通过对蚊密度的动态趋势预测来预警乙脑发生的可能性,为在防控乙脑疫情中病媒生物监测资料的利用提供一种有效方法。
1 材料与方法 1.1 蚊密度资料来源根据《全国病媒生物监测方案(试行)》蚊密度监测方法,汇总河北省2009—2016年11个设区市各监测点蚊虫种群密度和季节消长资料。河北省蚊密度监测时间为每年的4—10月。本研究蚊密度统计与分析中将1—3月和11—12月蚊密度设定为0只/(灯·h)。
1.2 蚊媒传染病资料来源河北省2009—2016年蚊媒传染病报告病例资料来自河北省传染病疫情网。
1.3 分析方法用SPSS 21.0软件对河北省蚊密度以及乙脑的地区分布和季节变化趋势进行分析,采用季节乘积ARIMA模型对蚊密度进行数据处理与分析。通过方差分析比较河北省总蚊密度的地区和季节分布差异是否有统计学意义,同时根据Pearson相关分析,分析乙脑与蚊密度季节消长关系;根据Bayes判别分析评价乙脑与总蚊密度的关系以及ARIMA模型对总蚊密度预测值和乙脑发生的关联程度。
1.3.1 ARIMA模型方法原理[7]及建模步骤利用时间序列的过去值及现在值预测未来值。季节性时间序列采用季节乘积模型ARIMA(p,d,q)(P,D,Q)s。P、Q为季节性的自回归和移动平均阶数,D为季节差分的阶数,s为季节周期。建模步骤:①通过分析得出序列的周期T;②序列平稳化;③模型的识别;④参数估计和检验;⑤预测:利用2009—2014年各月蚊密度数据建立模型,预测2015—2016年蚊密度并评估预测效果。
1.3.2 Bayes判别分析方法原理[7-8]及分析步骤根据掌握的已有每个类别的若干样本数据信息,建立判别函数,函数形式如下:Y=a1X1+a2X2+…anXn。本研究中,Y为是否有乙脑发生的判别指标,X为蚊密度变量,a为变量的判别系数。将河北省总蚊密度代入判别函数方程,分值高的即为判别指标所属类别。分析步骤:①训练样本和验证样本的设立;②建立评价函数模型;③判定待测数据;④判别效果评价:用符合率和误判率衡量,将训练样本和验证样本的判别结果分别与原发生结果进行对比。
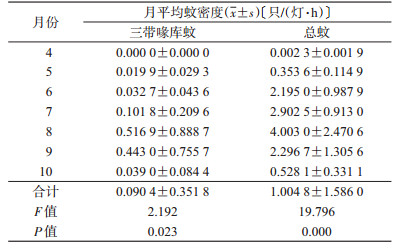
2 结果 2.1 河北省蚊密度ARIMA模型建立 2.1.1 蚊密度季节消长河北省三带喙库蚊(Culex tritaeniorhynchus)和总蚊密度均呈现5月开始上升,9月开始下降的季节趋势。三带喙库蚊密度季节差异有统计学意义(F=2.192,P=0.023),8、9月为三带喙库蚊密度高峰期,密度分别为0.516 9和0.443 0只/(灯·h);总蚊密度季节差异亦有统计学意义(F=19.796,P=0.000),8月为总蚊密度高峰期,密度为4.003 0只/(灯·h)。
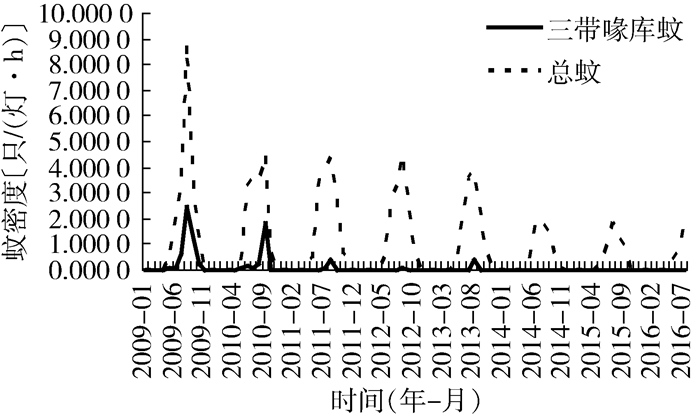
2009—2016年三带喙库蚊和总蚊密度均呈现逐年递减趋势,三带喙库蚊月平均密度为0.090 4只/(灯·h),总蚊月平均密度为1.004 8只/(灯·h)。三带喙库蚊与总蚊密度呈正相关(r=0.680,P=0.000),见表 1、图 1。
|
|
| 图 1 2009年1月至2016年7月河北省蚊密度趋势变化情况 Figure 1 The trend variation of mosquito density in Hebei province from January 2009 to July 2016 |
| |
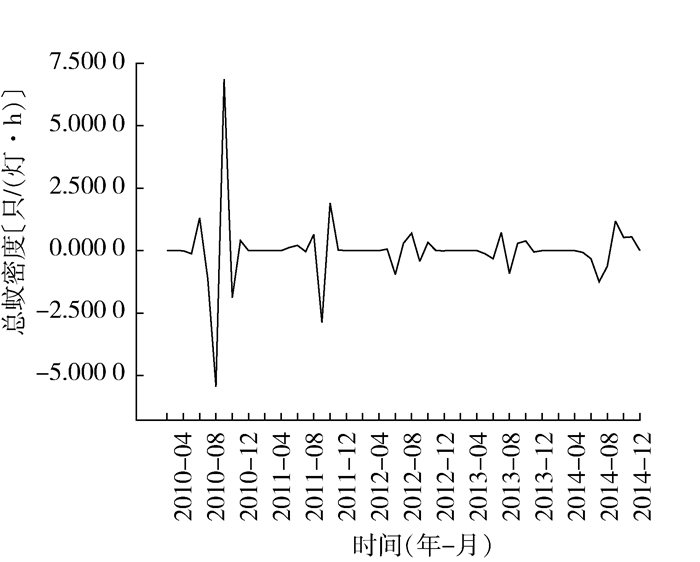
2009—2014年河北省总蚊密度呈明显的逐年递减趋势和每年8月为蚊密度高峰期的周期性,季节周期为12个月,属于非水平平稳序列,见图 1。为使数据的平稳性满足ARIMA模型需要,对原始数据分别进行1阶季节性差分和1阶非季节性差分消除趋势及季节影响,得到一个近似平稳的随机序列,见图 2。
|
| 图 2 经一阶非季节性差分和一阶季节性差分后的蚊密度序列图(12个月为1个周期) Figure 2 Autocorrelogram of time series of monthly mosquito density after two difference correction |
| |
根据差分转换次数得到ARIMA模型d=1,D=1,以12个月为1个周期。对差分平稳后的时间序列做ACF和PACF图,见图 3。

|
| 图 3 原序列经差分后的自相关和偏自相关图 Figure 3 Autocorrelogram and partial autocorrelogram of time series of monthly rodent density after difference correction |
| |
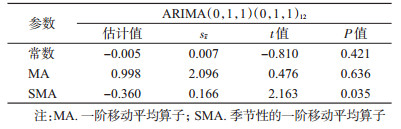
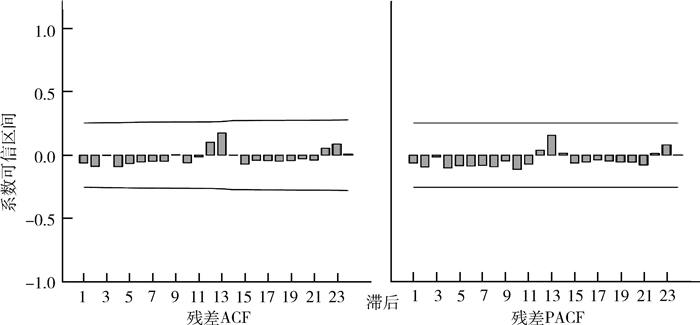
根据平稳后序列的ACF和PACF图,自相关函数在q=1步截尾,偏自相关系数拖尾,因此p=0,q=1;差分后序列的自相关和偏自相关函数在k=12时均显著不为0,可以考虑建立ARIMA模型:s=12,d=1,D=1,p=0,q=1,P=0或1,Q=0或1。对几个备选模型的统计量进行分析,根据平稳的R2越大拟合优度越好,标准化贝叶斯信息准则(BIC)值越小拟合越好原则,同时根据模型参数结果最终选取ARIMA(0,1,1)(0,1,1)12为最佳模型(平稳的R2=0.51,平均绝对误差MAE=0.509,BIC=0.106)。Ljung-Box方法检验得出残差为白噪声序列(Q=6.604,P=0.980),残差序列的ACF和PACF均在95%CI内,残差为随机性误差,见图 4。根据选定模型的参数估计得到模型数学表达式:(1—B)(1—B12)Yt=(1—0.998B)(1+0.36B12)et,其中Yt为时间序列模型在t时间的预测值,B为后移算子,et为时间序列模型在t时间的误差,见表 2。
|
| 图 4 ARIMA(0,1,1)(0,1,1)12模型残差自相关和偏自相关图 Figure 4 Autocorrelogram and partial autocorrelogram of residual errors from the ARIMA (0, 1, 0)×(0, 1, 1)12 |
| |
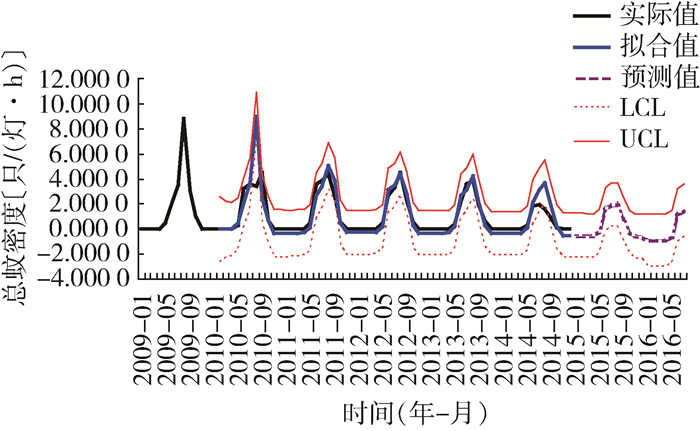
根据已建模型对2015—2016年蚊密度进行预测,蚊密度预测值的动态趋势与实际蚊密度基本一致,季节规律基本相同,实际蚊密度均在预测值的95%CI范围内,表明该模型能够应用于河北省蚊密度的预测,见图 5。
|
| 图 5 2009—2016年蚊密度实际值与模型拟合值以及预测蚊密度95%CI分布 Figure 5 Time series of actual, fitted and predicted mosquito density in Hebei province, 2009-2016 |
| |
河北省总蚊密度与各设区市蚊密度的多重线性回归拟合结果显示,衡水、邯郸、沧州、唐山、保定、邢台市的标准化偏回归系数分别为0.345、0.245、0.165、0.121、0.115和0.089,秦皇岛、张家口、廊坊、承德和石家庄市的标准化偏回归系数分别为0.064、0.025、0.022、0.021和0.015,前6个市的蚊密度对河北省总蚊密度的影响较后5个市影响更大一些,其中衡水市对河北省影响最大,标准化的偏回归系数为0.345。
2.2 蚊密度对乙脑的影响 2.2.1 蚊虫密度地区分布河北省三带喙库蚊地区分布差异有统计学意义(F=4.252,P=0.000),主要集中在邯郸、衡水等地,其中沧州、石家庄、张家口市未监测到三带喙库蚊。总蚊密度在河北省的地区分布差异亦有统计学意义(F=10.941,P=0.000),主要来源于衡水、邯郸、沧州、保定、唐山、邢台等地数据的影响,见图 6。

|
| 图 6 2009—2016年河北省蚊密度地区分布 Figure 6 The regional fluctuation of mosquito density in Hebei province from 2009 to 2016 |
| |
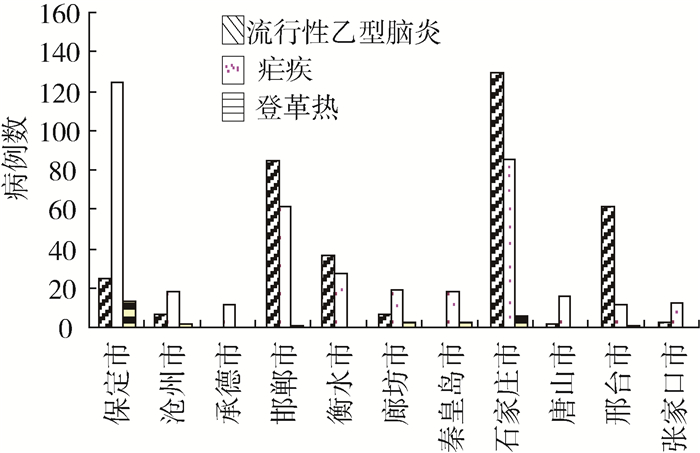
河北省2009—2016年蚊媒传染病病例共823例,其中乙脑本地病例369例,疟疾输入病例423例,登革热输入病例31例,主要蚊媒传染病地区分布见图 7。
|
| 图 7 2009—2016年河北省主要蚊媒传染病地区分布 Figure 7 The regional fluctuation of mosquito-borne diseases in Hebei province from 2009 to 2016 |
| |
2009—2016年河北省报告乙脑病例数呈现除2013年明显增加,其余各年整体平稳的状态,9—10月为乙脑发病高峰期。2013年出现乙脑病例暴发,病例主要分布在石家庄、邯郸、邢台、衡水、保定市等河北省中南部农村地区的农业人口中,乙脑报告病例数的增加是当年蚊媒传染病曲线峰值升高的主要原因(图 8)。

|
| 图 8 2009—2016年河北省蚊媒传染病发病情况 Figure 8 The situation of mosquito-borne diseases in Hebei province from 2009 to 2016 |
| |
河北省2009—2016年三带喙库蚊密度高峰为8—9月,总蚊密度高峰为8月,乙脑的发病高峰为9—10月,说明乙脑的流行与媒介蚊虫存在明显的季节关联。
对蚊虫监测数据和乙脑报告病例进行统计学处理,河北省三带喙库蚊月监测密度的月份间差异与迟后1个月有无乙脑发生无统计学意义(t=-1.480,P=0.144),2个月亦无统计学意义(t=-0.892,P=0.375);但是蚊密度高峰后2个月有无乙脑月份间的总蚊密度差异有统计学意义(t=-2.583,P=0.012),说明乙脑的发病高峰与总蚊密度高峰之间具有延迟性,见图 9。

|
| 图 9 2009—2016年河北省总蚊密度与乙脑病例的时间分布 Figure 9 The seasonal fluctuation of mosquito density and Japanese encephalitis in Hebei province from 2009 to 2016 |
| |
筛选河北省各市发生乙脑病例的年份,对三带喙库蚊月平均密度与依次推迟2个月后的乙脑月平均发病数做相关分析显示,河北省三带喙库蚊密度与乙脑无相关性(r=0.000,P=0.999);对总蚊月平均密度与依次推迟2个月后的乙脑月平均发病数做相关分析显示,河北省总蚊密度与乙脑呈正相关(r=0.101,P=0.043)。
2.3 Bayes判别分析应用于总蚊密度对乙脑发病的预测预警 2.3.1 训练样本和验证样本的设立将河北省2009—2014年总蚊密度作为训练样本建立判别函数,河北省2015—2016年总蚊密度作为验证样本考核判别函数的判别效果。
2.3.2 建立评价函数建立线性Bayes判别函数Y1=C01+C11X1+C21X2+…+Cm1Xm;Y2=C02+C12X1+C22X2+…+Cm2Xm;YG=C0G+C1GX1+C2GX2+…+CmGXm。其中,G为判别结果分类数,m为判别指标数,CmG为判别系数。
对于总蚊密度与乙脑发病的关系,假定group1代表蚊密度高峰2个月后无乙脑发生,group2代表蚊密度高峰2个月后有乙脑发生,X代表总蚊密度,则判别函数group1= C01+C11x;group2=C02+C12x。利用训练样本进行Bayes判别研究(先验概率设为0.5,即2个月以后是否发生乙脑概率相同),得到:C01=-0.759,C11=0.123,C02=-0.949,C12=0.242。即判别函数group1=-0.759+0.123x;group2=-0.949+0.242x。
2.3.3 判定待测数据,评价判别效果将训练样本和验证样本中需要判定的总蚊密度代入2个方程,可以得到group1、group2的具体值,取最大值作为初步判定该蚊密度下2个月后有乙脑发生的类别。
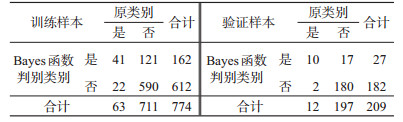
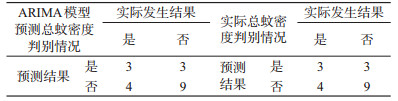
训练样本的每月总蚊密度代入函数并判断归属后,与原发生乙脑报告结果比较,总的误判率为0.184 8,符合率为0.815 2;验证样本的每月总蚊密度代入函数并判断归属后,与原发生乙脑报告结果比较,总的误判率为0.090 9,符合率为0.909 1,见表 3。
|
训练样本和验证样本判定结果与原发生结果对比误判率分别为0.184 8和0.090 9,表明总蚊密度影响乙脑报告病例数,利用总蚊密度高峰判别2个月后是否发生乙脑的判别性能良好,Bayes分析法可以很好地应用于总蚊密度对乙脑发生状况预测预警。
2.4 Bayes判别分析验证蚊密度ARIMA预测模型对乙脑发生情况的预警效果 2.4.1 河北省2015—2016年总蚊密度ARIMA模型预测值判别分析2个月后乙脑发生情况设定group1代表 2个月后无乙脑发生,group2代表 2个月后有乙脑发生,X代表河北省总蚊密度预测值。通过Bayes判别分析得到判别函数:group1=-0.868+0.765x;group2=-0.895+0.822x。将各月预测总蚊密度值代入函数并判别归属后,与乙脑实际发生状况比较符合率为0.631 6。表明利用时间序列模型对河北省总蚊密度的预测值判别2个月后是否发生乙脑的性能良好,能够对河北省乙脑发生状况进行预测预警。
2.4.2 河北省2015—2016年总蚊密度监测实际值判别分析2个月后乙脑发生情况利用河北省2015—2016年总蚊密度监测值进行Bayes判别分析,预测2个月乙脑发病状况,得到判别函数:group1=-0.863+0.901x;group2=-0.988+1.189x。判断归属后与原乙脑发生结果比较符合率为0.631 6。
利用河北省总蚊密度监测值和建立的ARIMA模型对预测2个月后乙脑发病状况符合率为100%,验证了蚊密度ARIMA模型能够很好地应用于河北省乙脑的预测预警,见表 4。
|
河北省近10年来乙脑主要媒介三带喙库蚊和监测到的总蚊密度均呈现逐年递减趋势,影响蚊密度的多种因素之间存在着复杂的关系,静态的因果结构模型很难揭示其流行趋势。时间序列动态模型是根据事物自身变动规律建立的一种行之有效的预测分析方法,已广泛应用于传染病预测等多种领域[3, 9]。河北省2009—2014年蚊密度监测值具有明显的趋势性和周期性,ARIMA模型在分析时间序列的随机性、平稳性和季节性的同时,可以建立适当的模型进行中短期预测[10]。采用ARIMA模型对河北省2009—2014年蚊密度进行拟合分析,最终筛选ARIMA(0,1,1)(0,1,1)12为最优模型,验证2015—2016年蚊密度预测值与实际值拟合较好,模型整体预测较理想。
河北省2009—2016年累计报告蚊媒传染病病例823例,其中乙脑病例占总病例数的44.84%,各年均有病例报告,发病高峰为9—10月。经对河北省三带喙库蚊和总蚊密度与乙脑报告病例的统计学分析,三带喙库蚊月密度与有无乙脑发生差异无统计学意义,说明由于三带喙库蚊监测数值偏低,无法有效利用其监测值关联预测乙脑疫情。曾有报道,在对当地监测蚊虫进行乙脑病毒核酸检测中,因三带喙库蚊数量极少而采用构成占比高的淡色库蚊(Cx. pipiens pallens)为样本作为监测结果的评估依据[11],与本研究采用总蚊密度作为统计样本的方法一致。本研究中监测的总蚊密度与三带喙库蚊密度呈正相关(r=0.680,P=0.000),并呈现与三带喙库蚊同样的随机性、平稳性和季节性特点,用总蚊密度与乙脑报告病例发生状况进行统计分析,密度高峰后2个月有无乙脑的月份间总蚊密度差异有统计学意义(t=-2.583,P=0.012);筛选各市发生乙脑病例的年份,河北省总蚊密度与2个月后乙脑发病数呈正相关(r=0.101,P=0.043),说明河北省乙脑发生与总蚊密度存在关联,采用ARIMA模型对蚊密度进行预测并进行乙脑疫情预警有实际应用性。建模结果也显示,ARIMA模型能够较好地拟合总蚊密度趋势,总蚊密度的预测值可作为2个月后乙脑发生状况的影响因素,虽然乙脑的发病高峰与蚊密度高峰的时间延迟会受到蚊虫叮咬传播时间、病毒增殖过程及病程潜伏期等诸多因素的影响[4],但其模型预测值和偏离常规的监测异常值的出现均可早期预警乙脑疫情。
Bayes判别分析[12]是根据先验概率求出后验概率,依据后验概率分布做出统计推断[13-16],通过计算待判定样本属于每个总体的条件概率,将样本归为条件概率最大的组。本研究利用河北省多年的蚊密度监测值和乙脑报告病例数,使用Bayes分类算法,从蚊密度监测值和ARIMA模型预测值数据出发,对是否发生乙脑进行分类预测,对比Bayes判别结果,验证ARIMA模型与乙脑的关系,探讨Bayes判别法应用于以总蚊密度作为影响因素判别乙脑发生状况的可能性。根据Bayes判别分析对2个月以后是否发生乙脑进行判别,训练样本和验证样本判别结果与原发病例报告结果进行对比的符合率分别为0.815 2和0.909 1,说明总蚊密度影响乙脑发生。进一步对新建ARIMA模型进行Bayes判别验证,对总蚊密度实际值和预测值Bayes判别预测2个月后乙脑发病情况,与原乙脑发生结果比较符合率均为0.631 6,且总蚊密度监测值与ARIMA模型预测值对2个月后是否发生乙脑的判别结果对应率为100%,说明利用ARIMA模型的总蚊密度预测值的Bayes判别方法对河北省乙脑疫情进行预测预警有比较高的灵敏性和稳定性。
乙脑作为一种蚊媒传染病,调查显示,河北省健康人群乙脑抗体的阳性率较低[17],因此,建立ARIMA模型对河北省总蚊密度的拟合预测,并采用Bayes判别分析可对早期预警防控河北省乙脑疫情具有重要实际作用。尹遵栋等[18]证实了时间序列分析在乙脑预测中的直接应用,其他相关研究也表明ARIMA模型是适宜可行的预测乙脑疫情的方法[19],能够指导乙脑防控。但是,ARIMA模型有时也会受到其他特殊或未知因素干扰导致对乙脑暴发流行不能进行有效预测,如河北省2013年乙脑疫情,虽然气候条件未见明显异常,总蚊密度监测值也未明显增加,但是乙脑在9—10月集中发病,病例主要为河北省中南部农村区域的农民[20],由于ARIMA模型使用的数据信息仅限于蚊密度监测值,不足以包含更多的其他未知的特殊影响因素,因此,2013年河北省利用ARIMA模型拟合预测的总蚊密度无明显升高,未能提示2013年乙脑预警,分析原因:①在媒介蚊虫的监测结果中存在既未将三带喙库蚊从总蚊中分离出来,总蚊密度也未明显升高或是还有其他原因;②三带喙库蚊作为乙脑病毒的主要传播媒介,国内外曾在10余种蚊虫中分离到乙脑病毒,提示乙脑病毒也可由多种蚊虫作为次要媒介传播的可能性[21-22];③乙脑病例在各市间的分布并不是完全按照各市间的总蚊密度大小分布,本次乙脑暴发多数病例来自石家庄市[23];④影响乙脑发病的因素除总蚊密度外,健康人群乙脑抗体水平、猪饲养情况、环境卫生状况、猪和蚊的乙脑病毒带病毒率等因素同时对乙脑发病起到重要作用[24]。
针对已建模型预测蚊密度并预警乙脑疫情的方法学研究,在利用病媒生物监测信息的同时,将拟合的ARIMA数学模型进一步应用于病媒生物(蚊虫)监测网络信息化系统[25-26],根据蚊密度与蚊媒传染病之间的关系,乘以相应系数作为网络监测系统中各地市蚊密度的预警值,结合蚊密度监测数据和动态趋势可快速进行预测预警,并采用Bayes判别分析可对早期预警蚊媒传染病疫情提供重要信息,特别是通过多重线性回归拟合显示的各地监测总蚊密度对汇总的总蚊密度的不同影响程度,可及时修正和更新ARIMA模型的拟合预测预警值,更科学准确地发挥对虫媒传染病的预警作用。
| [1] |
俞永新. 流行性乙型脑炎的全球流行动态及控制策略[J]. 中国公共卫生, 2000, 16(6): 567-569. DOI:10.11847/zgggws2000-16-06.74 |
| [2] |
许永刚, 魏亚梅, 张艳波, 等. 河北省2005-2007年流行性乙型脑炎监测分析[J]. 河北医药, 2009, 31(17): 2312-2313. DOI:10.3969/j.issn.1002-7386.2009.17.067 |
| [3] |
吕炜, 黄谊, 段丽琼, 等. 2007-2011年湖南省蚊媒传染病与蚊虫密度季节消长相关性分析[J]. 实用预防医学, 2012, 19(11): 1662-1664. DOI:10.3969/j.issn.1006-3110.2012.11.020 |
| [4] |
高文, 马丽华, 黄钢, 等. 河北省2013-2015年蚊媒传染病与蚊密度相关性分析[J]. 中国媒介生物学及控制杂志, 2016, 27(4): 350-353. DOI:10.11853/j.issn.1003.8280.2016.04.009 |
| [5] |
高文, 黄钢, 马丽华, 等. 差分自回归移动平均模型在河北省鼠密度监测信息系统中的应用研究[J]. 中国媒介生物学及控制杂志, 2017, 28(3): 265-268. DOI:10.11853/j.issn.1003.8280.2017.03.018 |
| [6] |
高围溦, 郭常义, 周义军. 时间序列分析在我国公共卫生领域的应用[J]. 中国社会医学杂志, 2014, 28(2): 78-80. DOI:10.3969/j.issn.1673-5625.2014.02.002 |
| [7] |
孙振球, 徐勇勇. 医学统计学[M]. 4版. 北京: 人民卫生出版社, 2015: 384-440.
|
| [8] |
李文杰. 判别分析在医学建模中的应用[J]. 兰州商学院学报, 2005, 21(3): 45-48. DOI:10.3969/j.issn.1004-5465.2005.03.011 |
| [9] |
魏亚梅, 郭娜娜, 韩旭, 等. 差分自回归移动平均模型在肾综合征出血热发病预测中的应用研究[J]. 中国媒介生物学及控制杂志, 2014, 25(3): 231-234. DOI:10.11853/j.issn.1003.4692.2014.03.010 |
| [10] |
易丹辉. 时间序列分析:方法与应用[M]. 北京: 中国人民大学出版社, 2011: 70-80.
|
| [11] |
袁明, 刘海博, 高艳青, 等. 北京首都第二机场建设前蚊媒监测结果分析[J]. 中国媒介生物学及控制杂志, 2015, 26(6): 622-624. DOI:10.11853/j.issn.1003.4692.2015.06.022 |
| [12] |
袁志发, 宋世德. 多元统计分析[M]. 2版. 北京: 科学出版社, 2000: 216-235.
|
| [13] |
裘炯良, 郑剑宁, 薛新春, 等. 国际航行船舶外来医学媒介生物传入风险的判别分析[J]. 现代预防医学, 2010, 37(4): 608-610. |
| [14] |
马庆波, 向华, 刘伟, 等. 基于贝叶斯-神经网络筛选矽肺早期标志物及建立诊断模型[J]. 质谱学报, 2011, 32(1): 50-54. |
| [15] |
杨珊, 周波, 何小群, 等. 贝叶斯判别分析在原发性醛固酮增多症诊断中的价值研究[J]. 中国实用内科杂志, 2015, 35(10): 835-838. |
| [16] |
肖培, 崔步云. 贝叶斯判别分析在布氏杆菌常见种别鉴定中的应用[J]. 中国卫生统计, 2013, 30(6): 802-804. |
| [17] |
魏亚梅, 韩旭, 韩占英, 等. 河北省健康人群流行性乙型脑炎抗体水平调查[J]. 实用预防医学, 2012, 19(8): 1160-1161. DOI:10.3969/j.issn.1006-3110.2012.08.014 |
| [18] |
尹遵栋, 罗会明, 李艺星, 等. 时间序列分析(自回归求和移动平均模型)在流行性乙型脑炎预测中的应用[J]. 中国疫苗和免疫, 2010, 16(5): 457-461. |
| [19] |
王磊.河北省流行性乙型脑炎流行特征分析及ARIMA预测研究[D].石家庄: 河北医科大学, 2008. http://cdmd.cnki.com.cn/Article/CDMD-11919-2008169224.htm
|
| [20] |
刘立, 王环宇, 张世勇, 等. 2013年石家庄市流行性乙型脑炎暴发疫情的流行病学分析[J]. 中国全科医学, 2016, 19(29): 3580-3583. DOI:10.3969/j.issn.1007-9572.2016.29.015 |
| [21] |
郑学礼. 我国蚊媒研究概况[J]. 中国病原生物学杂志, 2014, 9(2): 183-187. DOI:10.13350/j.cjpb.140222 |
| [22] |
邹志辉, 周健明, 林琳, 等. 深圳市龙岗区蚊虫自然感染流行性乙型脑炎病毒状况调查[J]. 现代预防医学, 2012, 39(19): 5083-5085. |
| [23] |
候雨丰, 翟士勇, 赵志清, 等. 石家庄市2013年乙脑媒介蚊虫调查分析[J]. 医学动物防制, 2015, 31(2): 216-217. |
| [24] |
林岩, 周勇, 潘伟毅, 等. 福建省儿童流行性乙型脑炎发病影响因素及控制策略研究[J]. 预防医学论坛, 2014, 20(11): 813-814. DOI:10.16406/j.pmt.issn.1672-9153.2014.11.028 |
| [25] |
蔡松武, 段金华, 刘文华, 等. 病媒生物网络直报信息系统在监测中的应用[J]. 中华卫生杀虫药械, 2010, 16(6): 415-417. |
| [26] |
杨天赐, 张晓斌, 董善定, 等. 智能蚊媒传染病应急管理系统开发与应用[J]. 中国卫生检验杂志, 2014, 24(5): 653-655, 660. |
 2018, Vol. 29
2018, Vol. 29