扩展功能
文章信息
- 潘衍宇, 吴海霞, 国佳, 刘起勇
- PAN Yan-yu, WU Hai-xia, GUO Jia, LIU Qi-yong
- 基于R语言自回归积分移动平均模型的广州市白纹伊蚊密度预测研究
- Population density prediction of Adeds albopictus in Guangzhou based on autoregressive integrated moving average model
- 中国媒介生物学及控制杂志, 2018, 29(6): 545-549
- Chin J Vector Biol & Control, 2018, 29(6): 545-549
- 10.11853/j.issn.1003.8280.2018.06.001
-
文章历史
- 收稿日期: 2018-06-22
- 网络出版时间: 2018-10-16 08:34
伊蚊在我国广泛分布,是黄热病、登革热、西尼罗热、寨卡病毒病等疾病的重要传播媒介[1-4]。自2013年以来,暴发寨卡病毒病疫情的国家和地区不断增加[5-6],尤其在美洲蔓延迅速,2016年寨卡病毒输入中国,目前虽无本地感染病例,但仍不能排除我国寨卡病毒病疫情暴发的潜在风险[7]。2016年12月巴西暴发黄热病,仅2017年7月至2018年2月,巴西政府就已报告黄热病病例464例,其中死亡病例达154例[8-9]。非洲、欧洲、中东为西尼罗热的传统病区[10-11],随着“一带一路”的深入发展,我国内陆同样面临西尼罗病毒侵入的危险。
蚊媒控制是防治此类传染病的最佳途径,有时甚至是唯一有效途径[12]。相比埃及伊蚊(Aedes aegypti),尽管白纹伊蚊(Ae. albopictus)长期以来一直被认为是次要的媒介生物,但其在近年来登革热和寨卡病毒病暴发流行中扮演着重要角色[4-6, 13-14]。有学者认为,白纹伊蚊也是未来中国登革热和其他病毒性疾病流行的重要风险因素[15]。自回归积分移动平均(autoregressive integrated moving average,ARIMA)预测模型相较复杂繁琐的马尔科夫链、人工神经网络预测等[16],其成熟简便,仅需常规监测资料即可进行预测,且非常适合具有季节周期性的原始资料。因此,建立白纹伊蚊密度ARIMA预测预警模型,可有的放矢地进行疾病防控工作,也可为合理分配卫生资源提供基线依据。
1 材料与方法 1.1 资料来源于中国CDC全国重要病媒生物监测系统收集2009年1月至2017年12月广州市白纹伊蚊密度监测资料,数据权威可靠。
1.2 研究方法 1.2.1 ARIMA模型ARIMA由Box和Bartholomew[17]于1970年共同提出,是一种经典的时间序列分析方法,又可细分为加法模型和乘法模型。其基本思想是对时间序列进行观察研究,从序列自相关的角度找出内在规律,利用其变化规律来预测将来的情况。因蚊虫密度变化具有明显的季节性,故选择ARIMA(p,d,q)(P,D,Q)s模型进行白纹伊蚊密度预测。其表达式为:

|
式中,θ(B)=1—θ1B—…—θqBq,Φ(B)=1—Φ1B—…—ΦqBq,θS(B)=1—θ1BS—…—θQBQS,ΦS(B)=1—Φ1BS—…—ΦPBPS。
1.2.2 模型构建与预测将2009年1月至2017年5月广州市诱蚊灯法捕获的白纹伊蚊资料按下列公式进行统一,建立数据库。

|
利用R 3.4.4将原始资料转为时间序列数据,进行纯随机序列检验(Box-Pierce test)(α=0.05),若P>0.05,即为纯随机序列,无建模必要。建模步骤分为以下4部分:
(1)序列平稳化:由于蚊虫的生长明显受到季节变化的影响,故可直接判定序列非平稳,进行季节性差分,然后根据差分后自相关图观察是否具有残留的长期趋势[17]。ARIMA(p,d,q)(P,D,Q)s模型中d为一般差分次数,D为季节性差分次数。差分后进行单位根检验(augmented Dickey-Fuller test,ADF test)(α=0.05),以检验序列是否具有残留的长期趋势或季节周期性,若P<0.05则说明差分后的序列平稳。
(2)模型定阶:通过差分后自相关图(autocorrelation function,ACF)、偏自相关图(partial autocorrelation function,PACF)大致判断短期相关模型与季节相关模型中自相关函数、偏相关函数最高阶数的取值。同时利用R语言forecast包,进行自动定阶。ARIMA模型的灵活之处就在于可以通过反复尝试,筛选出几组模型进行比较,从而选择相对最优模型。
(3)模型检验及参数估计:筛选出的模型其残差序列需满足白噪声、无短期相关性、方差齐性。进行白噪声检验(Ljung-Box test)(α=0.05),若P>0.05,即残差序列显著非零,为白噪声,残差序列中没有信息可继续提取[18],反之则需重新选择模型。同时观察残差ACF图,残差ACF图中若延迟阶数未超出2倍标准差,则残差序列无短期相关性且为白噪声,其结果与Ljung-Box test相互验证。
通过残差序列直方图,可判断残差是否存在异方差。
其最优模型的判断标准依据赤池信息量准则(akaike information criterion,AIC)与平稳R2,其中AIC值最小,平稳R2最大的模型为相对最优模型[19],最后利用最小二乘法对模型参数进行估计,并进行t检验,检验参数的统计显著性。
(4)模型拟合及预测:利用构建的ARIMA模型进行整体回代,将2009年1月至2017年5月白纹伊蚊密度预测值与实际值比较,评价指标为均方根误差(root mean square error,RMSE)、平均绝对误差(mean absolute error,MAE),由于平均相对误差(mean relative error,MRE)是相对指标,当某个实际值为0时,趋于∞,会严重失真,而白纹伊蚊密度包含0,故不用该指标衡量。同时描述2017年6—12月的预测值与实际值情况,评价外推效果。最后预测2018年1—12月白纹伊蚊密度数据。
2 结果 2.1 序列平稳化将数据进行Box-Pierce检验,χ2=44.014,P<0.05,即该序列显著非纯随机序列,可进行建模。由于蚊虫的生长明显受到季节变化的影响,故也可直接判断序列非平稳。观察时间序列图(图 1),未发现有明显长期变化趋势,因此仅进行一次季节性差分(D=1)。

|
| 图 1 广州市2009年1月至2017年5月白纹伊蚊密度原始序列 Figure 1 The original sequence of Aedes albopictus density in Guangzhou, January 2009-May2017 |
| |
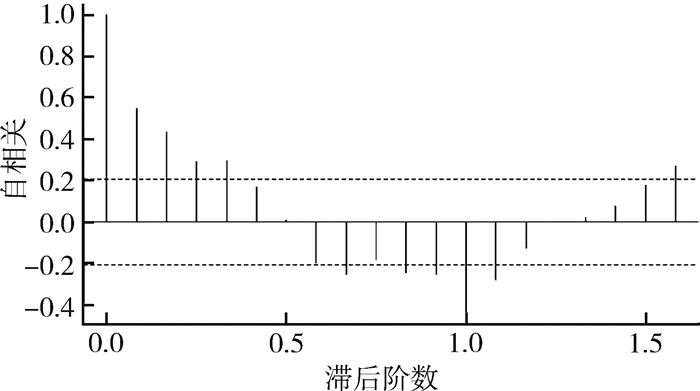
根据差分后ACF图(图 2),发现图形呈对三角形,具有典型的单调长期趋势特征,需再进行一次一般差分(d=1),以消除长期趋势。后经ADF检验(α=0.05),P=0.010,说明序列平稳。
|
| 图 2 经一次季节性差分的自相关图 Figure 2 The ACF diagram of first order deasonal difference |
| |
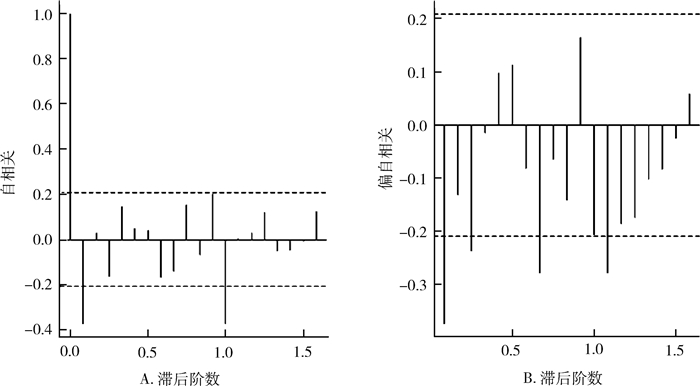
ACF图(图 3A)中自相关函数1阶显著非0,之后迅速收窄,向0趋近,如同“1阶之后高台跳水,溅起水花点点”是典型的截尾特征,PACF图(图 3B)拖尾,大致判断ARMA(0,1);季节自相关特征,自相关系数延迟12阶显著非0。偏相关系数延迟12阶落入2倍标准差内,大致判断季节性ARIMA(0,1)12,故拟合模型为ARIMA(0,1,1)(0,1,1)12。同时R语言自动定阶,最优模型为ARIMA(0,1,1)(2,1,0)12。
|
| 图 3 经一次一般差分、一次季节差分后自相关与偏自相关图 Figure 3 The ACF and PACF diagram after first order difference and first order seasonal difference |
| |
ARIMA(0,1,1)(0,1,1)12中AIC=-268.83,平稳R2=0.427;ARIMA(0,1,1)(2,1,0)12中AIC=-255.57,平稳R2=0.368,明显ARIMA(0,1,1)(0,1,1)12相对最优。尝试建立ARIMA(0,1,1)(0,1,1)12模型,结果见表 1。
根据
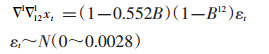
|
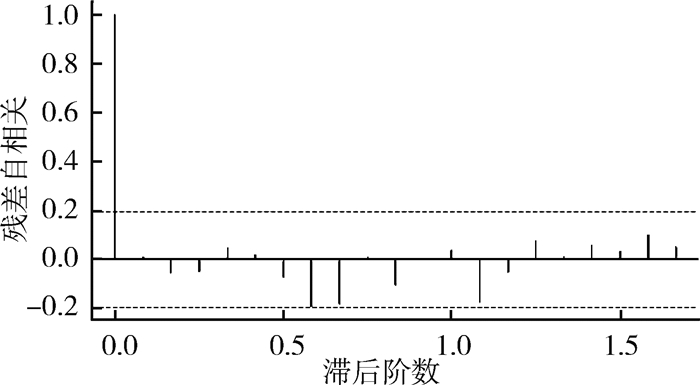
白噪声检验,P=0.992,可认为残差序列为白噪声,时间序列中有用信息已被充分提取,观察残差ACF图(图 4),发现延迟阶数均未超出2倍标准差界限,同样可认为残差自相关系数为0。
|
| 图 4 残差自相关图 Figure 4 Residual ACF diagram |
| |
至此,ARIMA模型的构建前提是默认残差序列方差齐性,即随着时间的推移,其残差序列的方差始终为一常数,实际上这一假定条件并不总是满足。由预测误差正态分布图(图 5)可判断,该残差序列大致服从均值为0的正态分布。

|
| 图 5 预测误差正态分布 Figure 5 Normal distribution of forecast errors |
| |
模型参数进行检验,|t1| =5.697>2.086,|t2|=5.076>2.086,差异均有统计学意义(P<0.05),说明参数不显著为0。
2.3 模型拟合由图 6可以看出,模型拟合曲线与实际值基本重合,绝大多数均在可信区间内,仅有个别实际值超出可信区间。

|
| 图 6 ARIMA乘积季节模型拟合曲线 Figure 6 Fitted curve of ARIMA model |
| |
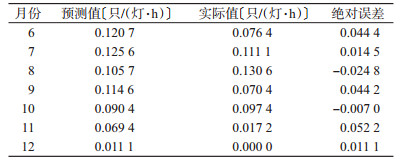
将数据进行整体回代,其中RMSE=0.040 9,MAE=0.026 5,表明ARIMA(0,1,1)(0,1,1)12模型构建科学有效。将模型预测的2017年6月至2017年12月白纹伊蚊密度数据与实际值比较,结果见表 2,其中RMSE=0.087 4,MAE=0.028 3,外推效果较好。
|
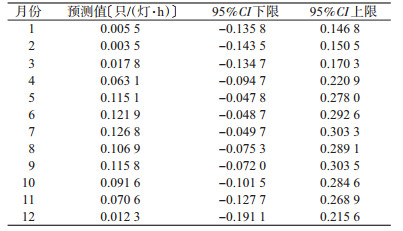
利用模型对2018年白纹伊蚊密度进行预测(表 3),其中7月白纹伊蚊密度最高,为0.126 8只/(灯·h),2月最低,为0.003 5只/(灯·h),1月次之。提示1、2月白纹伊蚊密度近似为0,与2009—2017年中1、2月白纹伊蚊密度绝大多数情况相同。构建广州市2018年白纹伊蚊密度预测曲线,见图 7。
|

|
| 图 7 ARIMA季节乘积模型广州市白纹伊蚊密度预测结果 Figure 7 Forecast result of Aedes albopictus density by ARIMA model |
| |
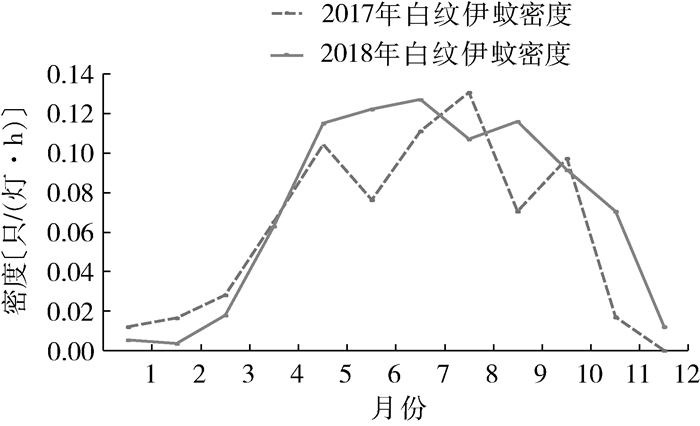
广州市2018年白纹伊蚊密度预测值与2017年白纹伊蚊密度实际值比较,1—4月小幅下降,之后迅速升高。除8、10月外,其余月份白纹伊蚊密度均高于2017年相应月份,但整体波动与2009—2017年白纹伊蚊密度比较变化不大,见图 8。
|
| 图 8 广州市2017—2018年白纹伊蚊密度 Figure 8 Comparison of Aedes albopictus density, in 2017—2018 |
| |
基于ARIMA模型的预测有一个前提条件是假定未来一段时间的条件与现在的条件相似,如疟疾的发病率由于“中国消除疟疾行动计划(2010—2020年)”的开展,发病率呈断崖式下降,应用ARIMA模型进行预测便不可靠,蚊虫密度的预测也是要建立在这一大的假设前提之下,且时间跨度越大,不确定性就越大。
有些文献表明,气候因素与媒介传染病发病率具有相关性[20-21],但笔者并未将气候因素纳入模型的构建。Siriyasatien等[22]曾利用蚊虫密度与气候资料建立疟疾发病率预测模型,但在预测白纹伊蚊密度这种微观数据中,本模型平稳R2达到0.427,代表模型已经捕获到42.70%的变异度,也即该模型可以解释白纹伊蚊密度变异程度的42.70%,剩余的57.30%可能受上千个因素影响,因此纳入其他若干因素为自变量似乎已无较大意义。
3.2 构建ARIMA模型的意义 3.2.1 早期预警对于疫情监测人员来说,发现传染病暴发流行的潜在隐患是一项重要工作,也是当前工作的难题。在早期预警工作中可利用95%预测区间设立警戒线,当实际蚊虫密度明显高于其警戒线时,表明蚊虫密度的变化情况已不同于以往的变化规律,此时应警惕蚊虫数量的暴发,加强灭蚊工作,避免蚊媒传染病的暴发[23]。因此,建立适合本地情况的蚊虫密度预测预警模型,具有现实意义。
3.2.2 防治措施效果的评价将开展相关防治工作后的实际数据设为实验组,模型预测数据为对照组进行比较,比较自身前后对照、空白对照,其时间顺序增强了可比性,且基于同一基线数据,可有效排除混杂因素,从而更加准确的评价防治效果,进行成本-效果分析,该法方便经济。
| [1] |
Huhtamo E, Cook S, Moureau G, et al. Novel flaviviruses from mosquitoes:mosquito-specific evolutionary lineages within the phylogenetic group of mosquito-borne flaviviruses[J]. Virology, 2014, 464-465: 320-329. DOI:10.1016/j.virol.2014.07.015 |
| [2] |
Wu JY, Lun ZR, James AA, et al. Dengue fever in mainland China[J]. Am J Trop Med Hyg, 2010, 83(3): 664-671. DOI:10.4269/ajtmh.2010.09-0755 |
| [3] |
Tran A, L'Ambert G, Balança G, et al. An integrative eco-epidemiological analysis of West Nile virus transmission[J]. Ecohealth, 2017, 14(3): 474-489. DOI:10.1007/s10393-017-1249-6 |
| [4] |
Marabuto E, Rebelo MT. The Asian tiger mosquito, Aedes (Stegomyia) albopictus (Skuse), a vector of dengue, chikungunya and Zika viruses, reaches Portugal (Diptera:Culicidae)[J]. Zootaxa, 2018, 4413(1): 197-200. DOI:10.11646/zootaxa.4413.1.10 |
| [5] |
Bhatt S, Gething PW, Brady OJ, et al. The global distribution and burden of dengue[J]. Nature, 2013, 496(7446): 504-507. DOI:10.1038/nature12060 |
| [6] |
Weetman D, Kamgang B, Badolo A, et al. Aedes mosquitoes and Aedes-borne arboviruses in Africa:current and future threats[J]. Int J Environ Res Public Health, 2018, 15(2): 220. DOI:10.3390/ijerph15020220 |
| [7] |
刘起勇. 寨卡病毒媒介伊蚊控制策略和措施展望[J]. 中国媒介生物学及控制杂志, 2016, 27(2): 93-98. DOI:10.11853/j.issn.1003.8280.2016.02.001 |
| [8] |
Hamer DH, Angelo K, Caumes E, et al. Fatal yellow fever in travelers to brazil, 2018[J]. MMWR Morb Mortal Wkly Rep, 2018, 67(11): 340-341. DOI:10.15585/mmwr.mm6711e1 |
| [9] |
World Health Organization. Yellow fever-Brazil. Disease outbreak news. Geneva, Switzerland: World Health Organization[EB/OL]. (2018-02-27)[2018-05-01]. http://www.who.int/csr/don/27-february-2018-yellow-fever-brazil/en/.
|
| [10] |
Chancey C, Grinev A, Volkova E, et al. The global ecology and epidemiology of West Nile virus[J]. Bio Med Res Int, 2015, 2015: 376230. DOI:10.1155/2015/376230 |
| [11] |
Beck C, Jimenez-Clavero MA, Leblond A, et al. Flaviviruses in Europe:complex circulation patterns and their consequences for the diagnosis and control of West Nile disease[J]. Int J Environ Res Public Health, 2013, 10(11): 6049-6083. DOI:10.3390/ijerph10116049 |
| [12] |
孟凤霞, 王义冠, 冯磊, 等. 我国登革热疫情防控与媒介伊蚊的综合治理[J]. 中国媒介生物学及控制杂志, 2015, 26(1): 4-10. DOI:10.11853/j.issn.1003.4692.2015.01.002 |
| [13] |
Ferreira-de-Lima VHF, Lima-Camara TN. Natural vertical transmission of dengue virus in Aedes aegypti and Aedes albopictus:a systematic review[J]. Parasit Vectors, 2018, 11: 77. DOI:10.1186/s13071-018-2643-9 |
| [14] |
Wong PSJ, Li MZI, Chong CS, et al. Aedes (Stegomyia) albopictus(Skuse):a potential vector of Zika virus in Singapore[J]. PLoS Negl Trop Dis, 2013, 7(8): e2348. DOI:10.1371/journal.pntd.0002348 |
| [15] |
Wu F, Liu QY, Lu L, et al. Distribution of Aedes albopictus (Diptera:Culicidae) in northwestern China[J]. Vector Borne Zoonotic Dis, 2011, 11(8): 1181-1186. DOI:10.1089/vbz.2010.0032 |
| [16] |
Zhang XY, Liu YY, Yang M, et al. Comparative study of four time series methods in forecasting typhoid fever incidence in China[J]. PLoS One, 2013, 8(5): e63116. DOI:10.1371/journal.pone.0063116 |
| [17] |
Bartholomew DJ. Time series analysis forecasting and control[J]. J Oper Res Soc, 1971, 22(2): 199-201. DOI:10.1057/jors.1971.52 |
| [18] |
Burns P. Robustness of the Ljung-Box test and its rank equivalent[J/OL]. (2002-07-18)[2018-05-01]. https://ssrn.com/abstract=443560. DOI: 10.2139/ssrn.443560.
|
| [19] |
Bozdogan H. Model selection and Akaike's Information Criterion (AIC):the general theory and its analytical extensions[J]. Psychometrika, 1987, 52(3): 345-370. DOI:10.1007/BF02294361 |
| [20] |
Benitez MA. Climate change could affect mosquito-borne diseases in Asia[J]. Lancet, 2009, 373(9669): 1070. DOI:10.1016/S0140-6736(09)60634-6 |
| [21] |
Reiter P. Climate change and mosquito-borne disease:knowing the horse before hitching the cart[J]. Rev Sci Tech, 2008, 27(2): 383-398. DOI:10.20506/rst.issue.27.2.38 |
| [22] |
Siriyasatien P, Phumee A, Ongruk P, et al. Analysis of significant factors for dengue fever incidence prediction[J]. BMC Bioinformatics, 2016, 17: 166. DOI:10.1186/s12859-016-1034-5 |
| [23] |
Olliaro P, Fouque F, Kroeger A, et al. Improved tools and strategies for the prevention and control of arboviral diseases:a research-to-policy forum[J]. PLoS Negl Trop Dis, 2018, 12(2): e0005967. DOI:10.1371/journal.pntd.0005967 |
 2018, Vol. 29
2018, Vol. 29



