扩展功能
文章信息
- 葛军旗, 李镜辉, 马永康, 龚正达
- GE Jun-qi, LI Jing-hui, MA Yong-kang, GONG Zheng-da
- 基于信息熵的动物鼠疫流行强度定量化初探
- The preliminary quantitative description of epidemic intensity in enzootic plague based on information entropy theory
- 中国媒介生物学及控制杂志, 2018, 29(5): 439-441
- Chin J Vector Biol & Control, 2018, 29(5): 439-441
- 10.11853/j.issn.1003.8280.2018.05.004
-
文章历史
- 收稿日期: 2018-06-11
- 网络出版时间: 2018-08-03 17:13
2 中国疾病预防控制中心传染病预防控制所, 北京 102206;
3 云南省地方病防治所, 云南 大理 671000;
4 云南省寄生虫病防治所, 云南 普洱 665000
2 National Institute for ommunicable Disease Control and Prevention, Chinese Center for Disease Control and Prevention;
3 Yunnan Institute of Endemic Diseases Control and Prevention;
4 Yunnan Institute of Parasitic Diseases Control and Prevention
任何学科逐步成熟的重要标志,就是它的一些重要概念从定性走向定量化[1]。在鼠疫防控工作中,动物鼠疫流行强度的大小通常根据动物鼠疫发生的疫点数、流行面积或检菌量等来主观评估划分[2-4],一直缺乏客观的定量化描述,导致鼠疫防控工作中积累的大量珍贵疫情资料未得到充分挖掘利用,无法与宿主动物监测资料、媒介蚤类监测资料和重要环境因素等进行深入的统计学分析。
信息熵概念最早由Shannon[5]提出,可以测度系统状态的复杂程度,在诸多学科领域都得到广泛应用[6],近年来在鼠疫宿主多样性、媒介蚤多样性及其与鼠疫流行关系研究方面也有应用[7-9],为鼠疫疫源地复杂生态系统研究提供了新途径。本研究尝试使用信息熵,根据疫点数来测量家鼠型动物鼠疫的流行强度。
1 材料与方法 1.1 数据来源在家鼠型鼠疫疫源地,动物鼠疫疫点被定义为具备动物鼠疫诊断标准之一的自然村或街道,构建用于家鼠型动物鼠疫流行强度计算的模拟数据,参数包括疫情年份、疫情发生乡镇和疫点数3个要素,设某年某县发生了8个疫点、乡(镇)数≥8,共构建出22种疫点分布状态。云南省盈江和陇川县1982-2005年的动物鼠疫疫情数据来源于云南省地方病防治所。
1.2 研究方法为了区别于信息熵H,用Ia表示鼠疫的流行强度,它被定义为一定时空范围内疫点数量及分布特征的度量。
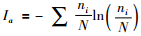
|
式中,Ia为监测县某年的动物鼠疫流行强度;ni为监测县该年每个乡镇的动物鼠疫疫点数;N为监测县该年的动物鼠疫总疫点数。
由于鼠疫具有传播速度快的特点,假设首发疫点周围一定范围内的疫点具有同质性。公式中把这个空间范围定义为乡(镇),因为乡(镇)具有以下特点:①地域跨度小、景观异质性相对较低;②乡(镇)间面积相差不大(个别间会有较大的差异),便于比较;③疫情资料易于收集。时间范围则以1年为单位。统计某监测县某年发生动物鼠疫疫情的乡镇数,每个乡(镇)的疫点数ni,该县该年份的总疫点数N,代入上式,就可以得出该年该监测县动物鼠疫的流行强度Ia。为区分无疫情和仅1个乡(镇)有疫情的情况,在定义无疫情时,Ia=0;仅1个乡(镇)有疫情时,Ia=Ia-2s,为该监测县动物鼠疫的平均流行强度,s为标准差。
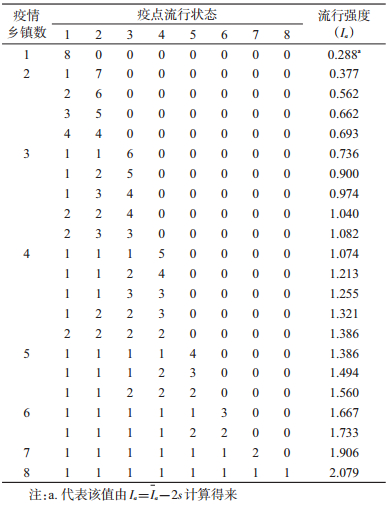
2 结果 2.1 模拟数据的流行强度计算8个疫点在某县有(乡镇数≥8)22种疫点分布状态,分别计算其流行强度Ia(表 1)。从Ia计算结果可以看出,疫点数相同时,一个县范围内发生动物鼠疫疫情的乡(镇)数越多,动物鼠疫的流行强度越大;乡(镇)数相同时,疫点在各乡(镇)中分布越均衡,动物鼠疫的流行强度越大。反之,发生动物鼠疫疫情的乡(镇)数越少,或动物鼠疫疫情越相对集中于某些乡(镇),动物鼠疫的流行强度越小。
|
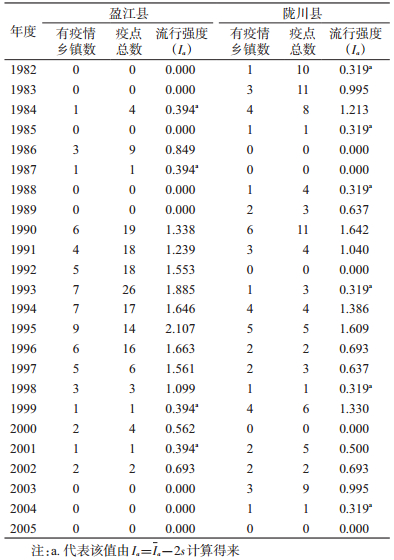
用云南省盈江和陇川县1982-2005年家鼠型动物鼠疫疫情数据分别计算动物鼠疫流行强度Ia(表 2),验证Ia在实际工作中的效果及作用。从计算结果可以看出,盈江和陇川县动物鼠疫流行强度最大的年份分别出现在1995年(2.107)和1990年(1.642);盈江县动物鼠疫流行强度最大的年份出现在1995年(Ia=2.107),而不是发生疫点数最多的1993年(1.885)。对2个县Ia做Spearman相关分析,相关系数为0.301(P=0.150),显示2个县动物鼠疫流行情况不存在统计学上的关联。
|
疫点数和流行面积都是基于空间广度动物鼠疫流行状态的简单数学描述。疫点数虽不及流行面积精确,但比流行面积更易获得,通常作为判断动物鼠疫流行强度的指标之一。然而,以疫点数评估动物鼠疫流行强度存在缺陷,其忽视了动物鼠疫流行的层次结构。在动物鼠疫流行中,存在一点暴发与多点暴发的区别。以家鼠型鼠疫为例,若仅有一个首发疫点[10],其他疫点在首发疫点周围排列,提示极有可能是一次流行,即一点暴发;而倘若有2个或以上的首发疫点,其他疫点在各自首发疫点周围排列,则可能是多点暴发。即使疫点数或流行面积相同,这两种情形的流行强度也是不等同的,后者的流行强度明显大于前者。
也有以鼠疫菌检出量来划分动物鼠疫流行强度的报道[3]。但鼠疫菌检出量受鼠疫静息期特性和流行期采样量影响[10-11]:静息期时,鼠疫菌检出率极低;流行期时,鼠疫菌检出率迅速增高,此时检测鼠类数量越多,鼠疫菌检出量越大[10]。因此,以鼠疫菌检出量作为判断动物鼠疫流行强度的指标并不合适。
鼠疫疫情控制时需要划定疫点和疫区,因而在长期的鼠疫防控工作中积累了大量的疫点和疫区资料。基于这些资料,应用信息熵测量动物鼠疫流行强度是传染病流行强度定量化描述的有益尝试。对于每个鼠疫自然疫源地的每一时刻均能计算1个流行强度,从而使同一疫源地的不同时间阶段、同类型的多个疫源地之间产生可比性,符合鼠疫疫情统计分析发展的需要,有助于深入探讨鼠疫的流行规律。
动物鼠疫流行强度Ia具有时间属性、地域性和层次性,权衡了鼠疫的流行特点,初步证明能够较好地度量动物鼠疫流行强度。但是,流行强度Ia只是流行状态的信息度量,它并不代表动物间鼠疫流行的实际情况,能否真正适用于动物鼠疫流行强度的描述尚需开展更深、更广泛的研究。
 2018, Vol. 29
2018, Vol. 29

