扩展功能
文章信息
- 高文, 黄钢, 马丽华, 王喜明, 韩晓莉
- GAO Wen, HUANG Gang, MA Li-hua, WANG Xi-ming, HAN Xiao-li
- 差分自回归移动平均模型在河北省鼠密度监测信息系统中的应用研究
- Application of autoregressive integrated moving average (ARIMA) model in information system for rodent surveillance in Hebei province
- 中国媒介生物学及控制杂志, 2017, 28(3): 265-268
- Chin J Vector Biol & Control, 2017, 28(3): 265-268
- 10.11853/j.issn.1003.8280.2017.03.018
-
文章历史
- 收稿日期: 2017-02-14
- 网络出版时间: 2017-04-11 17:06
鼠类作为传染源或自然疫源性疾病的储存宿主,可传播多种疾病。河北省多年来以《全国病媒生物监测方案(试行)》为基础建立覆盖全省城镇人居环境的鼠类监测体系,掌握鼠密度季节消长情况。时间序列分析法是利用一系列由时间顺序记录数据得到事物随时间变化规律的常用统计分析方法[1]。本研究利用2008-2015年河北省鼠密度数据,采用差分自回归移动平均(ARIMA)模型拟合河北省鼠密度资料,探讨模型的可行性,对鼠密度的动态趋势及实际鼠密度异常值进行预测和预警,预防鼠传疾病的传播。
1 材料与方法 1.1 资料来源根据《全国病媒生物监测方案(试行)》鼠密度监测方法,在河北省11个市分别选择城镇居民区、特殊行业和农村自然村作为监测点,采用夹夜法,于2008-2014年每月对鼠类种群、密度和季节消长进行监测,并对监测数据进行时间序列分析。
1.2 统计学分析利用Excel 2003软件录入河北省2008-2014年的鼠密度数据,用SPSS 21.0软件分析河北省主要鼠种密度的季节变化趋势,通过χ2检验比较河北省主要鼠种的季节分布差异是否有统计学意义并采用ARIMA模型进行数据处理与分析。
1.2.1 建立模型基本原理与方法[2]将预测对象随时间推移而形成的数据视为一个随机序列,用一定的数学模型表达式来拟合该序列,进而利用模型根据时间序列的过去值和现在值预测未来值。
ARIMA(p,d,q)中,AR为自回归,p为自回归项数,MA为移动平均,q为移动平均项数,d为时间序列成为平稳序列所做的差分次数(阶数)。
1.2.2 ARIMA模型建模步骤① 序列平稳化:对非平稳序列进行差分处理转化为平稳序列;② 建立可能模型:根据自相关函数(ACF)和偏相关函数(PACF)特征,建立几种可能的模型;③ 参数估计和检验:估计和验证可能模型的参数,检验参数是否有统计学意义,残差序列是否为白噪声;④ 预测应用:利用2008-2014年各月鼠密度数据建立模型,预测2015年鼠密度并评估预测效果,进一步将模型应用于短期预测。
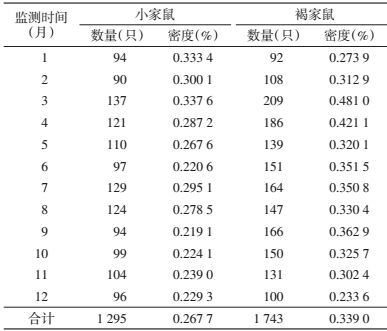
2 结果 2.1 河北省2008-2015年鼠种构成及季节分布共捕获鼠类3 082只,月平均密度为0.644 0%。其中小家鼠(Mus musculus)占捕获总数的42.02%,褐家鼠(Rattus norvegicus)占56.55%,月平均密度分别为0.267 7%和0.339 0%,两鼠种季节分布差异无统计学意义(χ2=19.601,P=0.051),见表 1。
|
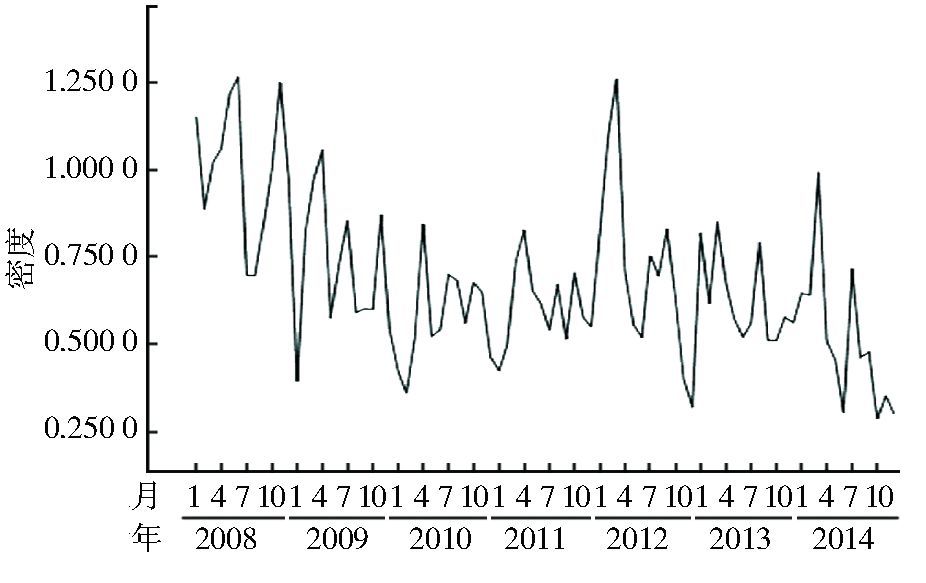
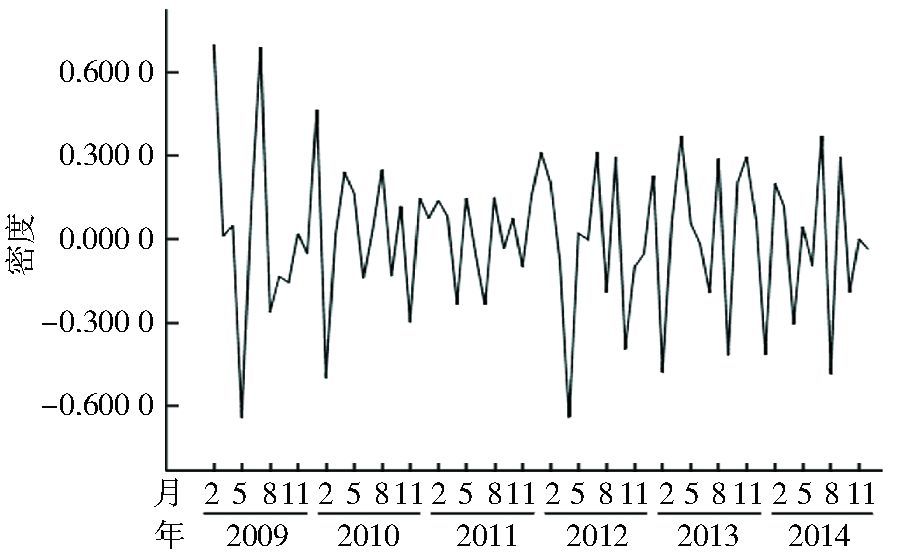
将2008-2014年河北省鼠密度绘制成时间序列图,各年鼠密度均呈明显的趋势性和周期性。每年在3-4月和7-8月出现2个鼠密度高峰;除2012年出现1次上升,2008-2014年河北省鼠密度整体呈逐年递减趋势,属于非水平平稳序列,见图 1。为使数据的平稳性满足ARIMA模型需要,对原始数据分别进行1次季节性差分和1次非季节差分以消除趋势和季节影响,随机序列近似平稳,见图 2。
|
| 图 1 2008-2014年河北省鼠密度时间序列图 Figure 1 Time series of monthly rodent density during 2008-2014 |
| |
|
| 图 2 经一阶非季节性差分和一阶季节性差分后的鼠密度序列图(12个月为1个周期) Figure 2 Auto-correlogram of time series of monthly rodent density after two difference correction |
| |
根据差分转换次数,初步确定模型ARIMA(p,1,q)×(P,1,Q)12,其中p、q和P、Q分别表示连续模型和季节模型的自回归阶数和移动平均阶数,12表示季节模型以12个月为周期。对差分后的时间序列做ACF和PACF图(图 3)。

|
| 图 3 原序列经差分后的ACF和PACF图 Figure 3 Auto-correlogram and partial autocorrelogram of time series of monthly rodent density after difference correction |
| |
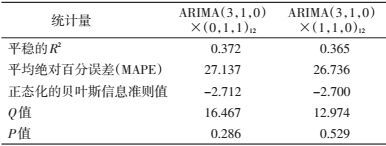
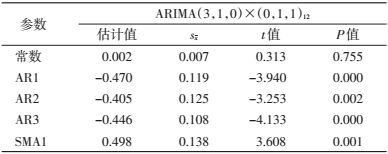
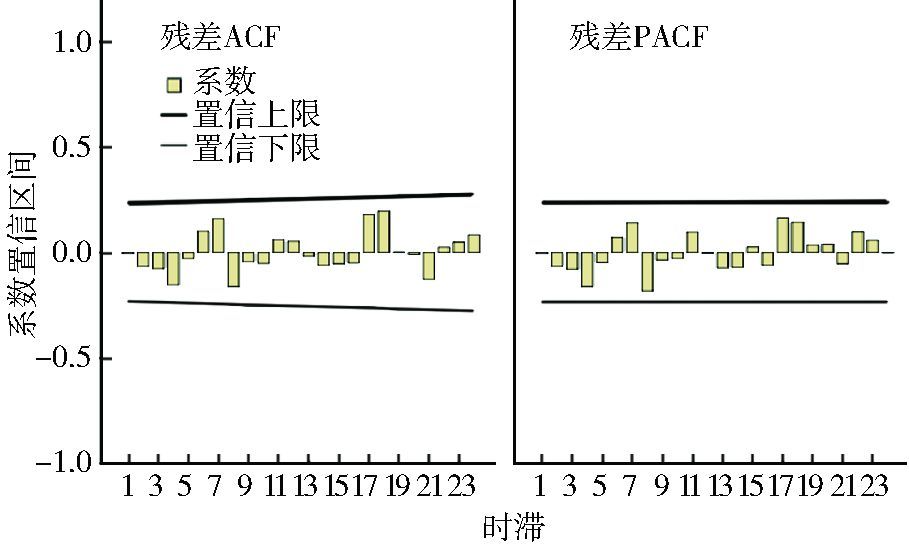
根据差分后序列的ACF和PACF图从低阶到高阶对p、q、P、Q进行调试检验,根据模型的检验结果和参数,最终选定模型ARIMA(3,1,0)×(1,1,0)12和ARIMA(3,1,0)×(0,1,1)12为备选模型。对两个备选模型的统计量进行分析,按照标准化贝叶斯信息准则(BIC)值最小准则得到最佳模型ARIMA(3,1,0)×(0,1,1)12,标准化BIC值为-2.712,见表 2。采用Ljung-Box方法检验残差白噪声,残差序列的ACF和PACF均在95%CI范围内,见图 4。残差为白噪声序列(Q=16.467,P=0.286),表明残差为随机性误差,且模型中的参数检验有统计学意义,见表 3。因此,ARIMA(3,1,0)×(0,1,1)12模型为最优模型。模型数学表达式:(1+0.47B+0.405B2+0.446B3)(1-B)(1-B12)Yt=(1-0.498B12)et。
|
| 图 4 ARIMA(3,1,0)×(0,1,1)12模型残差AC和PACF图 Figure 4 Auto-correlogram and partial autocorrelogram of residual errors from the ARIMA (3, 1, 0) × (0, 1, 1)12 |
| |
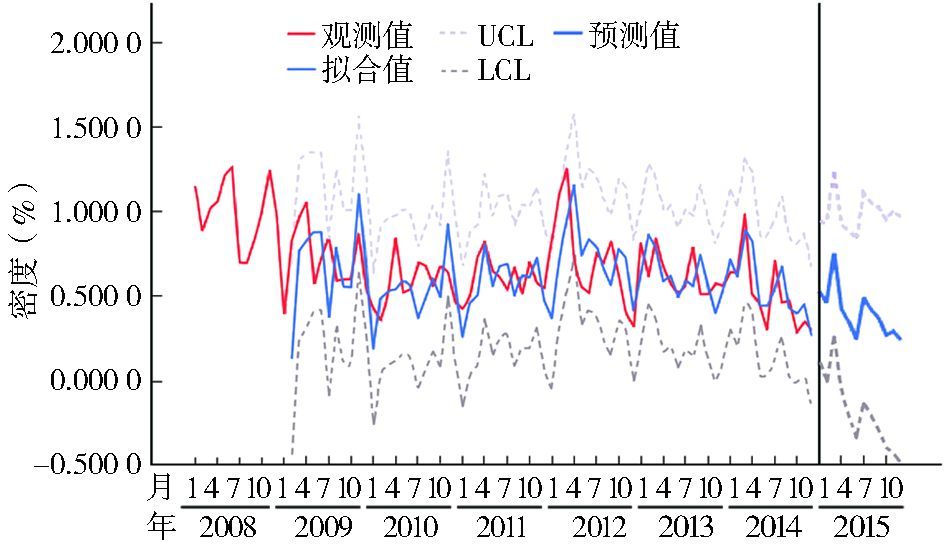
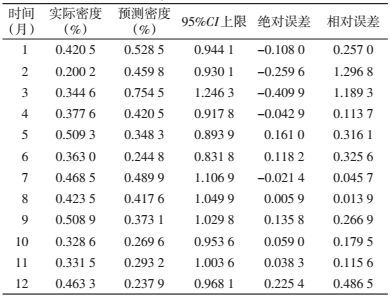
根据建立的预测模型对2015年鼠密度进行预测,各月预测值同实际鼠密度整体动态趋势一致,季节规律基本相同。预测值与实际值的平均相对误差为0.383 9,实际值均在预测值的95%CI范围内,且利用该模型预测的鼠密度季节消长趋势与实际情况基本一致,表明该模型能较好地拟合实际鼠密度,可用于预测鼠密度(图 5、表 4)。利用该模型对鼠密度进行中短期预测,根据鼠密度的季节变化规律,若实际鼠密度在预测值95%CI范围内波动,表明种群消长正常;若超出预测值95%CI上限,提示鼠密度异常,应警惕鼠传疾病风险,为鼠传疾病的预测预警提供依据。
|
| 图 5 2008-2015年鼠密度实际值与模型拟合值以及预测鼠密度95%CI分布 Figure 5 Time series of actual, fitted and predicted rodent density in Hebei province during 2008-2015 |
| |
|
鼠类是多种疾病的重要传播媒介,严重危害人类健康。本研究结果显示,2008-2015年河北省城镇主要鼠种为家鼠,且小家鼠和褐家鼠的季节分布差异无统计学意义,鼠总密度呈双峰曲线,3-4月和7-8月出现密度高峰,与其他省份鼠密度监测结果基本一致[3]。
家鼠可作为鼠疫的储存宿主,也是肾综合征出血热(HFRS)汉城型汉坦病毒的主要宿主。河北省以鼠类为自然宿主和主要传染源的传染病主要是HFRS,鼠密度与HFRS发病率呈正相关且差异有统计学意义,随着鼠密度的上升,HFRS发病率上升[4]。河北省的HFRS是以家鼠型为主的综合性疫区,且发病时间呈春冬季双峰分布,3-6月为大高峰,11-12月为小高峰[5],与此次调查结果一致。河北省HFRS的发病高峰期较监测到的鼠密度高峰期延迟2个月,时间延迟可能是病毒从鼠到人的传播过程、人感染病毒到HFRS发病潜伏期、人从发病到病例诊断的时间等多种原因所致。因此,利用时间序列法对鼠密度动态趋势进行连续监测和预测,可对实际鼠密度的异常情况进行预警,为鼠传疾病的发生发展提供依据;当鼠密度出现异常值时,应及时有效地开展灭鼠工作,对预防鼠传疾病传播有重要意义。
时间序列分析法是一种根据研究对象本身历史数据随时间变化的规律,利用历史数据建立数学统计模型进行外推的预测方法。ARIMA模型相对于其他预测模型,弥补了传统的因果回归分析法必须获得预测对象的影响因素以及其数据资料的缺陷,无需对时间序列的发展模式做出先验假设,同时可对模型进行反复识别和修改,预测精度较高[6]。河北省2008-2014年鼠密度具有明显的趋势性和周期性,且鼠密度受气候、环境和人类行为等多方面因素影响[7]。因此,利用ARIMA模型对河北省2008-2014年鼠密度资料进行拟合分析,最终筛选ARIMA(3,1,0)×(0,1,1)12为最优模型,预测值与实际值拟合较好,模型整体预测较理想。
病媒生物监测是各种病媒传染病防控的基础,是疾病预防控制中重要的系统性基础工作。病媒生物监测网络信息化建设可有效地改善以往病媒数据信息严重滞后及因手工统计失误导致的数据错误,提高了审核的准确性和一致性。时间序列预测模型与病媒生物监测信息系统相结合,在一定程度上强化了病媒生物日常监测的工作效率,起到实时监测、统计、预警的综合指导作用;同时减轻了人工汇总监测数据的工作强度,提高了监测质量和效率[8-9],为传染病防控工作提供了有力支持。ARIMA模型可用于鼠密度预测,将拟合的模型应用于病媒生物鼠类监测网络信息化系统,根据各地鼠密度与鼠传疾病发生状态间的关系[4-5],乘以相应系数作为网络监测系统中鼠密度的预警值,结合河北省上报鼠密度实际数据和动态趋势可更快速直观地进行预报预警,当实际鼠密度达到或超过预警值时,及时警惕,从而发现和预防潜在的疫情信息。
本研究ARIMA模型可较好地应用于鼠总密度的预测,该模型的预测方法在一种或几种特定鼠种的鼠密度预测中也有较好的推广价值。不同鼠传疾病其主要传播宿主不同,本研究仅选取了人居环境进行调查,农田等未调查生境类型也可能存在其他优势种群,如黑线姬鼠(Apodemus agrarius)等可作为HFRS汉滩型汉坦病毒的主要宿主。因此,了解本地鼠种及其分布并结合当地鼠传疾病情况,探讨某种特定鼠传疾病时,可利用时间序列分析法对本地主要宿主的鼠密度及动态趋势拟合新模型进行单独预测预警,有针对性地采取防制措施,预防疾病的发生。
ARIMA模型在多领域预测中均得到较好的应用[10-13]。应用ARIMA模型时应注意:历史统计数据应≥50个,季节性乘积ARIMA模型时间序列数据至少有4个季节周期,若序列太短则可靠性太差;ARIMA模型只能用于中短期预测,若考虑长期预测,则需随时间的增加不断加入新的数据,并对模型中的参数进行修正和验证,重新拟合更合适的预测模型[14]。
| [1] | 郑磊, 刘德坚, 许贤. 时间序列分析法在肺结核发病率预测中的应用[J]. 实用预防医学, 2012, 19(11): 1729–1731. DOI: 10.3969/j.issn.1006-3110.2012.11.050 |
| [2] | 孙振球. 医学统计学[M]. 北京: 人民卫生出版社, 2002: 258-370. |
| [3] | 张家勇, 白玉银, 张稷博, 等. 辽宁省2009-2013年人居环境鼠类监测报告[J]. 中国媒介生物学及控制杂志, 2015, 26(2): 185–187. |
| [4] | 陶旭, 彭勋, 贾春辉, 等. 2005-2013年秦皇岛市肾综合征出血热宿主动物监测分析[J]. 职业与健康, 2015, 31(21): 2986–2988. |
| [5] | 韩占英, 韩旭, 魏亚梅, 等. 2008-2012年河北省肾综合征出血热监测及流行特征研究[J]. 中国人兽共患病学报, 2014, 30(9): 947–950. |
| [6] | 刘刚, 单芙香. ARIMA模型及其在麻疹发病率预测中的应用[J]. 数理医药学杂志, 2011, 24(4): 379–382. |
| [7] | 赵奇, 高丽君, 唐振强, 等. 河南省鼠密度监测及季节消长[J]. 中华卫生杀虫药械, 2015, 21(4): 390–392. |
| [8] | 蔡松武, 段金花, 刘文华, 等. 病媒生物网络直报信息系统在监测中的应用[J]. 中华卫生杀虫药械, 2010, 16(6): 415–417. |
| [9] | 赵楠, 张海艳, 王威, 等. 传染病疫情报告质量控制软件的设计开发[J]. 首都公共卫生, 2015, 9(4): 165–168. |
| [10] | 杨小兵, 汪鹏, 江高峰. ARIMA乘积季节模型在流行性腮腺炎发病率预测中的应用[J]. 公共卫生与预防医学, 2013, 24(6): 39–42. |
| [11] | 高围溦, 郭常义, 周义军. 时间序列分析在我国公共卫生领域的应用[J]. 中国社会医学杂志, 2011, 28(2): 78–80. |
| [12] | 李晓翠, 高琴, 谢和宾, 等. ARIMA模型在工伤职工人数分析中的应用[J]. 实用预防医学, 2012, 19(11): 1622–1625. DOI: 10.3969/j.issn.1006-3110.2012.11.007 |
| [13] | 魏亚梅, 郭娜娜, 韩旭, 等. 差分自回归移动平均模型在肾综合征出血热发病预测中的应用研究[J]. 中国媒介生物学及控制杂志, 2014, 25(3): 231–234. |
| [14] | 张文彤. 世界优秀统计工具SPSS 11统计分析教程-高级篇[M]. 北京: 北京希望电子出版社, 2002: 250-289. |
 2017, Vol. 28
2017, Vol. 28