扩展功能
文章信息
- 兰策介, 沈元, 游颖琦
- LAN Ce-jie, SHEN Yuan, YOU Ying-qi
- 以蚊虫为例浅析不同气温参数的多重共线性对建模的影响
- Effects of multicollinearity among common temperature parameters on model in the case of mosquitoes
- 中国媒介生物学及控制杂志, 2015, 26(4): 372-375
- Chin J Vector Biol & Control, 2015, 26(4): 372-375
- 10.11853/j.issn.1003.4692.2015.04.011
-
文章历史
- 收稿日期:2015-02-11
气温是影响某些昆虫种群消长的重要气象因子[1],也是在模型研究中应用较多的自变量。我国采用的气温参 数有虫密度获取当日的某种或几种气温参数[2, 3, 4, 5],或者在采样之前一定历期的气温参数[6]。在国外,有研究采用每日平均气温建立尖音库蚊(Culex pipiens pipiens)的交互关系模型[7],也有采用12、2、3月一定历期与气温相关的3个参数建立烦扰伊蚊(Aedes sollicitans)7月的发生量模型[8]。然而不同气温参数之间存在自相关[5, 6],但尚无研究给予论证。如果同时采用自相关显著的气温参数建立模型,该模型可能为复合函数,理论上只需应用其中一个气温参数[9]。为了解气温参数的多重共线性对建模的影响,本研究以蚊虫与气温的关系模型为例探讨了几种常用气温参数的多重共线性,为选用气温参数建立模型提供参考依据。 1 材料与方法 1.1 数据来源
2010年2月至2011年12月,以www.weather.com.cn网站上记录的无锡市区每天24个整点时刻的气温(℃)。再分别获得每天的平均气温(X1)、最高气温(X2)、最低气温(X3)、傍晚气温(X4)(18:00时的气温)以及自当日算起之前5天的5日均温(X5)5个气温参数的数据。以之前研究报道中建设用地(Ⅰ)9个监测点2010和2011年的蚊虫数据为例[10],分析蚊密度(Y)与气温参数的相关性。 1.2 数据分析方法
应用SPSS 13.0软件先做每2个气温参数的散点图,判断2个参数间的相关性类型,建立拟合回归线,获得各气温参数的相关性形式图。再利用相应的回归类型分析获得2个参数间的复相关系数(R)、决定系数(R2)、校正决定系数(Rc2),以及对回归模型系数项和常数项进行t 检验的显著性值(P)。
将蚊虫数量以10为底进行对数转换后作为因变量,以5个气温参数为自变量,采用向后法(Backward)的自变量选入方式,进行多元直线回归分析,获得R、Rc2和方差膨胀因子(VIF),以及对回归模型进行t 检验的显著性值(P)(Analyze>Regression>Linear)。当VIF∈(0,10)为多重共线性不存在,VIF∈[10,100)为多重共线性较强,VIF∈[100,+∞)为多重共线性严重。 2 结果 2.1 数据概况
从2010年2月26日至2011年12月9日,历时566 d,记录了459 d的气温数据,获得了298 d具有24个完整时刻的气温数据,以及140个具有5日完整时刻的5日均温数据。所记录的平均气温为21.5 ℃;最高气温为38.4 ℃,发生在2010年8月13日的15:00;最低气温为-0.5 ℃,发生在2010年3月11日的05:00。
同期,在9个监测点调查获得360台次的蚊虫样本,从中选取3月下旬至7月上旬的144个蚊虫样本作为分析对象,经调查日期和气温记录日期配对,最终获得22对完整的蚊虫和气温日期数据。 2.2 每2个气温参数之间的相关性分析
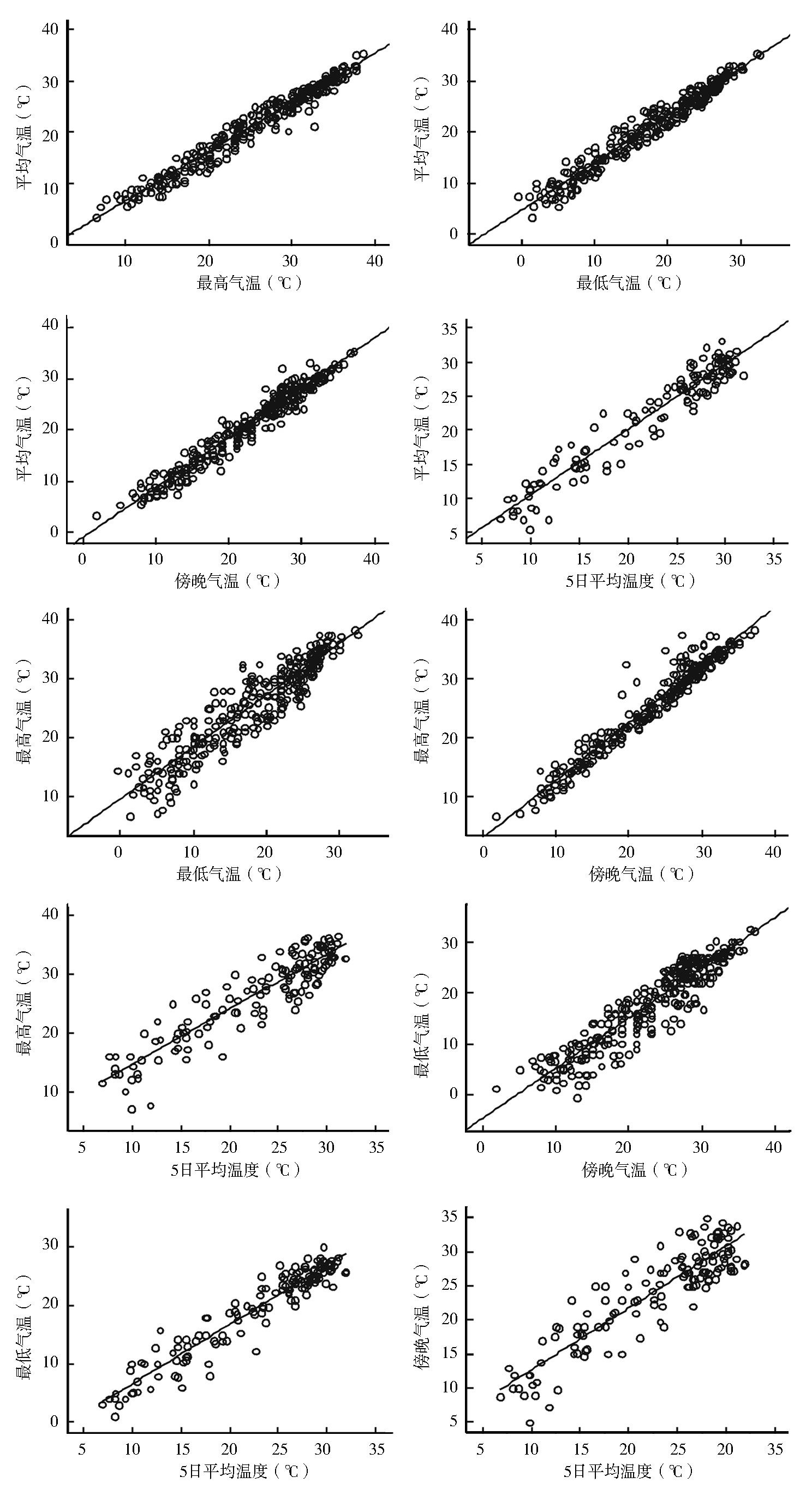
任意2个气温参数均呈明显的线性正相关,其中平均气温分别与最高气温、最低气温、傍晚气温的数据点集中分布在拟合线附近;最高气温和傍晚气温的极少数数据偏离拟合回归线,绝大部分数据也集中分布在拟合线附近;最低气温分别与最高气温和傍晚气温的数据分布相对较为分散,很大一部分数据点的分布偏离拟合线较多;5日均温与其他参数的数据分布也较为分散。各气温参数的拟合形式详见图 1。
|
| 图 1 各气温参数间的拟合回归线形式 Figure 1 Fitted regression lines between different air temperature parameters |
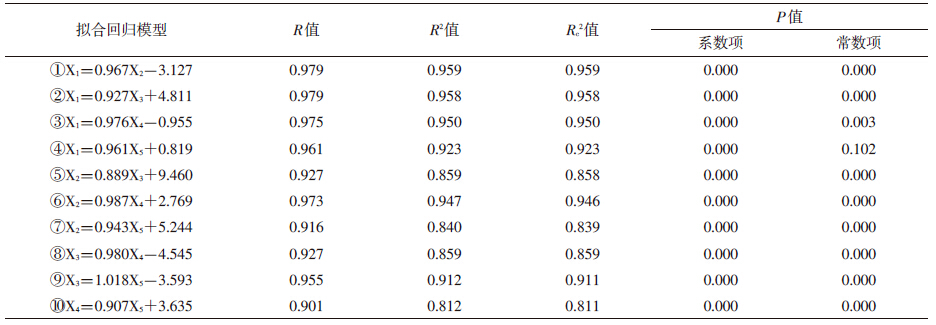
相关性分析显示(表 1),各气温参数之间均有较高的相关性,均R>0.9。平均气温分别与最高气温、最低气温、傍晚气温、5日均温回归的校正决定系数均>0.9;最高气温与傍晚气温的Rc2=0.946;最低气温与5日均温的Rc2=0.911。其他气温参数之间的Rc2<0.9。各气温参数之间回归模型的系数项和常数项经t检验,差异均有统计学意义(P<0.01)。
多元直线回归分析结果显示(表 2),当5个气温参数全部纳入方程时,R=0.800,Rc2=0.528。X1的VIF为470.5,存在严重的多重共线性;X2、X3、X4 均10<VIF<100,存在较强的多重共线性;X5的VIF为7.6,不存在多重共线性。经向后选入法筛选自变量后,随自变量数目的减少回归方程的R 值降低,Rc2值有升高的趋势,VIF也随之变化。筛选后仅纳入一个自变量X4时,回归方程的R 最低为0.775,Rc2值最高为0.581。
以蚊虫为例获得的回归方程显示(表 2),经向后法筛选自变量后,最后以傍晚气温为唯一自变量获得最优方程,而有的以平均气温和最高气温为最优自变量[3],也有以最低气温和20:00时刻气温为最优自变量[5]。一方面可能因为不同地区的蚊虫对气温的响应存在差异,另一方面可能因为分析的对象不同,前者研究的是三带喙库蚊(Culextritaeniorhynchus),后者研究的是白纹伊蚊(Aedesalbopictus),而本研究是以淡色库蚊(Cx. pipienspallens)为优势种的总蚊类[10]。
各气温参数之间相关性较高(图 1),均>0.9,并且均达到极显著水平(表 2),表明存在一定程度的共线性。与文献所述一致[5, 6],也符合客观现象。经多重共线性诊断(表 2),当5个气温参数均纳入方程时,方程的R值最高,但Rc2值最低。当自变量减少时,共线性强度降低,仅纳入2个自变量时,依然存在较强的多重共线性。只有一个自变量X4时,R 值虽然降低了,但是Rc2升高了。说明气温参数之间的多重共线性问题可能会高估回归方程的相关性,与文献叙述的基本一致,即随着自变量个数的增加,回归方程的复相关系数会不断增大,此时应该以Rc2值来判别方程的优劣[11]。
本研究只讨论了气温参数的多重共线性以及对蚊密度消长建模的影响,此外,日照时数、太阳辐照量、降雨量、风速等均与气温存在关联[12, 13],这些因子是否存在较强的多重共线性,以及对建模的影响尚不清楚。要充分了解不同气象因子的多重共线性,指导建立更加科学的回归模型,还需深入研究各因子之间的交互关系。
| [1] | 秦正积,罗超,孟言浦,等. 气温、湿度、降雨量对蚊密度的影响统计分析[J]. 中国媒介生物学及控制杂志,2003,14(6):421-422. |
| [2] | 吕芬,周平,黄新动,等. 白背飞虱灯下虫量与气象要素关系的相关分析[J]. 昆虫知识,2007,44(1):48-53. |
| [3] | 杨维芳,孙俊,徐燕,等. 三带喙库蚊发生量与气象因子相关性初步分析[J]. 中国媒介生物学及控制杂志,2010,21(1):49-50. |
| [4] | 兰策介,沈元,陆宏枫,等. 无锡市2006-2010年蚊虫群落监测分析[J]. 现代预防医学,2013,40(2):338-341. |
| [5] | 周毅彬,冷培恩,顾君忠,等. 上海市白纹伊蚊密度与气象因素关系的研究[J]. 中国媒介生物学及控制杂志,2014,25(5):405-407. |
| [6] | 卢衍凤,戴桂珍,卢正勇,等. 平和县1976年第一、二代三化螟蛾高峰日及灯下蛾量统计预报方法的探讨[J]. 福建师范大学学报:自然科学版,1976,11(2):87-102. |
| [7] | Morin CW,Comrie AC. Modeled response of the West Nile virus vector Culex quinquefasciatus to changing climate using the dynamic mosquito simulation model[J]. Int J Biometeorol,2010,54(5):517-529. |
| [8] | Walsh AS,Glass GE,Lesser CR,et al. Predicting seasonal abundance of mosquitoes based on off - season meteorological conditions[J]. Environ Ecol Stat,2008,15(3):279-291. |
| [9] | 同济大学数学教研室. 高等数学(上册)[M]. 4版. 北京:高等教育出版社,1996:24-25. |
| [10] | 沈元,孙俊,兰策介,等. 不同土地利用方式对蚊虫群落的影响[J]. 生态学杂志,2012,31(7):1751-1755. |
| [11] | 孙振球,徐勇勇. 医学统计学[M]. 2版. 北京:人民卫生出版社,2007:321-329. |
| [12] | 刘晶淼,丁裕国,黄永德,等. 太阳紫外辐射强度与气象要素的相关分析[J]. 高原气象,2003,22(1):45-50. |
| [13] | 王丽娟,陈正洪,李芬. 武汉地区太阳总辐射与气象要素的关系研究[J]. 太阳能,2011,32(17):15-18. |
 2015, Vol. 26
2015, Vol. 26