扩展功能
文章信息
- 吴伟, 郭军巧, 安淑一, 关鹏, 周宝森
- WU Wei, GUO Jun-qiao, AN Shu-yi, GUAN Peng, ZHOU Bao-sen
- 基于Elman反馈型神经网络的肾综合征出血热发病率预测模型
- Application of Elman feedback neural network model to predict the incidence of hemorrhagic fever with renal syndrome
- 中国媒介生物学及控制杂志, 2015, 26(4): 349-352
- Chin J Vector Biol & Control, 2015, 26(4): 349-352
- 10.11853/j.issn.1003.4692.2015.04.005
-
文章历史
- 收稿日期:2015-02-23
2 辽宁省疾病预防控制中心
2 Liaoning Center for Disease Control and Prevention
肾综合征出血热(HFRS)是由布尼亚病毒科的汉坦病毒属引起,包括汉坦病毒、汉城病毒、obravaBelgrade病毒和普马拉病毒[1]。HFRS流行范围广、病死率高,严重危害居民的生命健康,属于我国重点防治传染病之一。建立有效的预测模型对HFRS的防控有较强的实用价值。
神经网络具有非线性映射、自适应学习及鲁棒容错性等优良特性,使其能够较为精确地描述非线性的动态过程,已被广泛用于传染病发病率的预测。神经网络可分为前馈型和反馈型2种基本类型。前馈型网络通过引入隐含层及非线性转移函数可以实现复杂的非线性映射功能。但前馈型网络的输出仅由当前输入和权矩阵决定,而与网络先前的输出结果无关。反馈型神经网络的输入包括有延迟的输入或者输出数据的反馈,由于存在有反馈的输入,所以是一种反馈动力学系统。Elman神经网络是一种典型的反馈型神经网络,该模型在前馈型网络的隐含层中增加了一个承接层,作为一步延时的算子,信号可以在前向和后向两个方向进行传递[2]。因此,Elman神经网络可以记忆过去的状态,特别适合处理时间序列问题[3]。已有研究者使用该方法对伤寒[4]和手足口病[5]等传染病发病率的时间序列数据进行预测,并取得了良好效果。
本研究使用全国2004-2013年HFRS的月发病率资料,建立Elman反馈型神经网络预测模型,对2014年1-9月HFRS的月发病率进行预测。并将拟合及预测结果与SARIMA 模型进行比较,探讨Elman神经网络在HFRS发病率预测中的应用前景。 1 材料与方法 1.1 资料来源
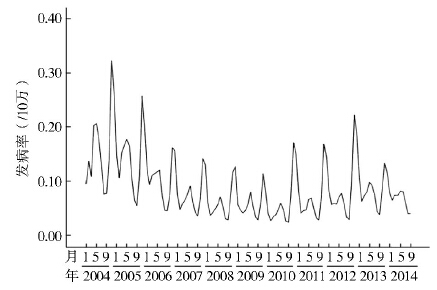
2004年1-9月HFRS月发病资料来源于历年逐月《卫生部公报》。人口资料来自历年《中国卫生统计年鉴》。HFRS月发病率序列见图 1。
|
| 图 1 全国2004年1-9月HFRS月发病率序列 Figure 1 Sequence chart of monthly incidence of HFRS in China from January to September,2014 |
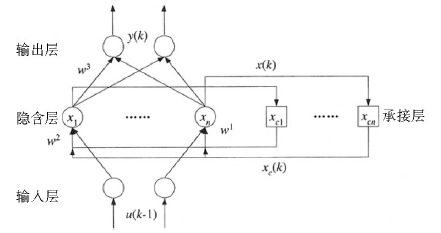
Elman神经网络是Elman于1990年提出的。其网络结构见图 2,一般分为4层:输入层、隐含层(中间层)、承接层和输出层。输入层、隐含层和输出层的连接类似于前馈型网络,输入层的单元仅起信号传输作用,输出层单元起线性加权作用。隐含层单元的传递函数可采用线性或非线性函数,承接层又称上下文层或状态层,它用来记忆隐含层单元前一时刻的输出值并返回给网络的输入,可以认为是一个一步延时算子。
|
| 图 2 Elman神经网络结构 Figure 2 Structure of Elman neural network |
以图 2为例,Elman神经网络的非线性状态空间表达式:
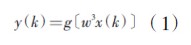

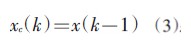
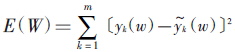 ,式中,
,式中,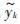 k(w)为目标输入向量。
1.3 Elman神经网络预测模型的建立
1.3.1 输入输出的选择
k(w)为目标输入向量。
1.3 Elman神经网络预测模型的建立
1.3.1 输入输出的选择
抽取x1~x13组成第1个样本,其中(x1,x2,…,x12)为输入变量,x13为输出变量;抽取x2~x14组成第2个样本,其中(x2,x3,…,x13)为输入变量,x14为输出变量,以此类推。使用2004年1月至2013年11月共108组数据作为训练样本的输入,2005年1月至2013年12月的数据作为训练样本的输出;以2013年1月至2014年8月共9组数据作为测试样本的输入,2014年1-9月的数据作为测试样本的输出。 1.3.2 网络的建立和训练
使用Matlab 7.0软件的神经网络工具箱编程构建HFRS发病率的Elman神经网络预测模型。隐含层神经元数目的选择目前还没有确切的理论和方法。研究者普遍认为与问题的要求及输入和输出单元的数量有直接关系[7]。本研究通过逐渐增加和减少隐含层神经元数目的方法,选择使网络具有足够泛化和输出精度的隐含层神经元数目,最后确定为10个隐含层神经元数目。最终,网络结构为12-10-1。隐含层选取tansig(S型正切函数)作为传递函数,输出层选择logsig(S型对数函数)作为传递函数,选择trainlm 作为训练函数,learngdm作为神经网络权值/阈值学习函数。网络反复训练10 000次。 1.4 SARIMA预测模型的建立[8]
SARIMA模型是在假定季节相关和普通相关交互作用下建立的乘法模型,可以用符号表示:SARIMA(p,d,q)×(P,D,Q)s。其中,p是简单模型的自回归阶数,P是季节模型的自回归阶数,d是简单模型的差分阶数,D是季节模型的差分阶数,q是简单模型的移动平均阶数,Q 是季节模型的移动平均阶数,s为周期,当随机事件的发展变化随着时间表现出季节性时,如果以月为单位,则s=12。SARIMA模型的建立按4个阶段进行:①序列平稳性检验及平稳化处理;②模型的识别;③模型参数估计和模型诊断;④预测应用。使用2004年1月至2013年12月的数据建立模型,使用2014年1-9月的数据检验模型的预测效果。使用IBMSPSS Statistics 22.0软件的专家建模器建立SARIMA模型,专家建模器可以自动筛选出最优的SARIMA模型。 1.5 效果评价[8]
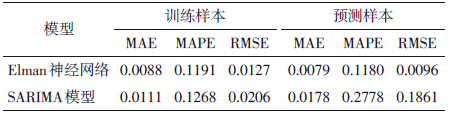
使用平均绝对误差(MAE)、平均绝对误差百分比(MAPE)以及均方误差平方根(RMSE)3个指标对Elman神经网络和SARIMA模型的拟合及预测效果进行评价。 2 结果
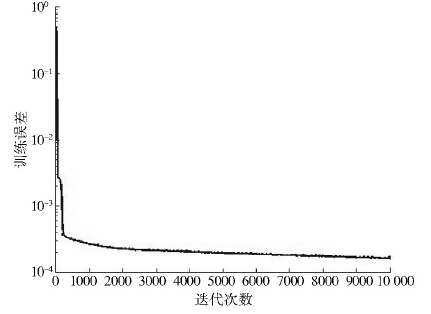
Elman神经网络经过10 000次训练后,其训练误差为0.000 16。网络训练误差迭代收敛曲线见图 3。
|
| 图 3 Elman神经网络误差迭代收敛曲线 Figure 3 Error iteration convergence curve of Elman neural network |
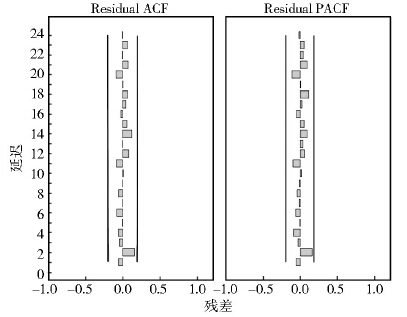
通过观察HFRS月发病率原始序列的自相关和偏自相关图,发现该序列为非平稳序列。原始数据在进行自然对数转换后,在一次普通差分的基础上再进行一次季节差分,序列变成平稳序列。IBM SPSSStatistics 22.0软件的专家建模器最终确定的最优时间序列模型结构为SARIMA(0,1,1)×(1,1,0)12。该模型最终通过了参数显著性检验。其残差的自相关和偏自相关系数均落在2倍标准差之内(图 4),残差序列可以认为是白噪声。
|
| 图 4 SARIMA模型残差的自相关和偏自相关 Figure 4 Autocorrelation and partial autocorrelation figure of SARIMA model residual |
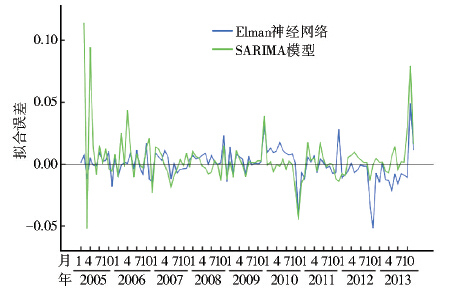
Elman神经网络和SARIMA模型的拟合误差曲线见图 5。Elman神经网络总体的拟合效果尚可,误差波动范围不是太大,只是对于个别拐点处时点的拟合误差稍大。而SARIMA模型在时间序列初段的拟合误差偏大。两种模型拟合效果的比较见表 1,对于训练样本,Elman 神经网络的MAE、MAPE 和RMSE均小于SARIMA模型。
|
| 图 5 Elman神经网络和SARIMA模型的拟合误差曲线 Figure 5 Fitting error curve of Elman neural network and SARIMA model |
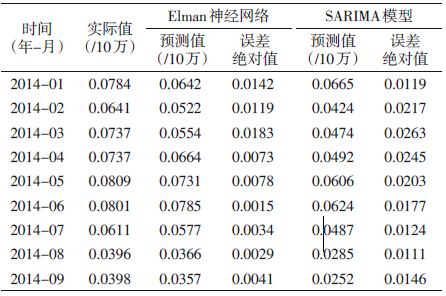
两种模型对全国2014年1-9月HFRS发病率预测值和实际值比较结果见表 2;两种模型预测效果的比较见表 1,对于预测样本,Elman神经网络的MAE、MAPE和RMSE均小于SARIMA模型。
 |
时间序列分析作为传统的线性模型分析手段,克服了影响预测对象的因素错综复杂、不易分析和数据资料不易得到的难题,以时间序列变量综合替代各种影响因素,模型的建立过程简单、经济、适用,短期预测精度较高[9]。但是,其缺点也比较明显,如非线性映射性能较弱,对于不规则数据序列难以确定合适的模型结构[10]。因此,对于HFRS发病率这类具有一定非线性特征的时间序列,其预测的精度往往难以令人满意。Elman神经网络是典型的动态神经元网络,是反馈网络在预测中使用较多的一种方法[11]。Elman神经网络的特点是隐含层的输出通过承接层的延迟与存储,自联到隐含层的输入,这种自联方式使其对历史状态的数据具有敏感性,内部反馈网络的加入增加了网络本身处理动态信息的能力,从而达到动态建模的目的[12]。本研究所建立的Elman神经网络总体拟合效果要优于SARIMA模型,但是对于个别拐点处时点的拟合误差还是有些偏大。造成这种现象的主要原因是因为本研究是按照时间序列数据来建立的模型,而影响HFRS发病的因素是多样的,这些因素并未能考虑到模型参数中。此外,Elman神经网络是通过学习输入模式来建模的,在网络的训练过程中,网络输出值需要反馈给输入神经元作为输入的一部分。这样,网络输出中存在的误差又会进入输入层。在这种反馈模式下的误差与其不确定性,可能会影响准确性。
传染病预测主要是指根据传染病的发生、发展规律和有关因素的历史资料,采用数学模型、分析判断等方法对其将来的发生、发展和流行趋势进行预测的一种方法。对于预测模型的建立是否成功最重要的一个判断依据是对未来疾病发生的预测准确性。预测准确性的高低可以根据MAE、MAPE以及RMSE等指标的大小进行判断,这些指标的值越小,说明模型预测准确性越高。本研究所建立的Elman神经网络模型预测结果的MAE、MAPE以及RMSE均小于SARIMA模型,说明Elman神经网络对于全国HFRS的预测效果优于SARIMA模型。根据已建立的Elman神经网络模型,我们可以根据模型的预测结果及早发现HFRS异常变化的苗头,发出警示,提醒相关工作人员提前做好预防控制措施,以达到保护居民生命健康的目的。相对于传统公共卫生监测,其最大的特点就在于对卫生事件反应的高度前瞻性,具有较强的推广应用价值。
| [1] | 石健. 我国肾综合征出血热流行病学研究进展[J]. 中国人兽共患病学报,2007,23(3):296-298. |
| [2] | Pham DT,Liu X. Training of Elman networks and dynamic system modelling[J]. Int J Syst Sci,1996,27(2):221-226. |
| [3] | 胡欢,林莉莎,陈文韬,等. 基于Elman 网络预测汇率短期发展趋势[J]. 经济数学,2014,31(2):19-22. |
| [4] | Zhang XY,Liu YY,Yang M,et al. Comparative study of four time series methods in forecasting typhoid fever incidence in China[J]. PLoS One,2013,8(5):e63116. |
| [5] | 张兴裕,冯海欢,肖雄,等. Elman神经网络在手足口病发病率预测中的应用初探[J]. 现代预防医学,2012,39(9):2136-2138,2141. |
| [6] | 王军生,包卫军. Elman 神经网络在银行间同业拆借利率分析中的应用[J]. 统计与信息论坛,2010,25(1):84-87. |
| [7] | 张慧斌,高秀萍. 基于Elman 神经网络的时间序列股票价格短期预测[J]. 山西大同大学学报:自然科学版,2011,27(2):5-7,60. |
| [8] | 张兴裕,张韬,刘元元,等. 小波神经网络在肾综合征出血热发病率预测中的应用[J]. 中国卫生统计,2012,29(6):864-865,870. |
| [9] | 韩琴,苏虹,王忱诚,等. ARIMA模型与GRNN模型对性病发病率的预测研究[J]. 现代预防医学,2012,39(6):1337-1340. |
| [10] | 严薇荣,徐勇,杨小兵,等. 基于ARIMA-GRNN组合模型的传染病发病率预测[J]. 中国卫生统计,2008,25(1):82-83. |
| [11] | 王婷婷,钱晓东. 时间序列的非线性趋势预测及应用综述[J].计算机工程与设计,2010,31(7):1545-1549. |
| [12] | 柴燕丽,孟令建. 基于神经网络的淮河流域年径流量预测模型[J]. 水资源与水工程学报,2009,20(1):58-61. |
 2015, Vol. 26
2015, Vol. 26