扩展功能
文章信息
- 肖珊, 陈建勇, 林斌, 龙建勋, 彭莱, 朱彩英
- XIAO Shan, CHEN Jian-yong, LIN Bin, LONG Jian-xun, PENG Lai, ZHU Cai-ying
- 自回归积分移动平均模型在长沙市蝇密度预测中的应用
- Fly density prediction based on autoregressive integrated moving average model in Changsha, China
- 中国媒介生物学及控制杂志, 2023, 34(6): 788-793
- Chin J Vector Biol & Control, 2023, 34(6): 788-793
- 10.11853/j.issn.1003.8280.2023.06.015
-
文章历史
- 收稿日期: 2023-05-15
蝇类作为重要病媒生物,能携带细菌、病毒、立克次体等多种致病微生物,可污染食物传播疾病,骚扰影响人们日常生活,威胁着人类的健康[1],是国家长期监测控制的病媒生物[2]。自回归积分移动平均模型(autoregressive integrated moving average,ARIMA)是重要的时间序列预测模型,由多个模型组合而成,利用蕴含在序列中的综合信息特征来预测未来数据走向,目前已广泛应用于各类传染病的发病预测中[3-4],近年来在病媒生物尤其是鼠类和蚊类的密度预测中也得到了一些应用[5-7]。蝇类生长繁殖受气候因素影响大,有明显的季节性,其密度数据呈现明显的季节变动规律,建立蝇密度季节性ARIMA模型可提前预测蝇密度趋势,为制定和评估防控策略提供科学依据。
1 材料与方法 1.1 数据来源本次研究仅使用现有数据,数据来源于长沙市疾病预防控制中心2005年1月-2022年12月的蝇密度监测数据,按照《全国病媒生物监测方案(试行)》及《全国病媒生物监测方案》,采用笼诱法进行监测。
1.2 研究方法ARIMA模型是一种重要的时间序列预测模型,由自回归模型、滑动平均模型及使时间序列平稳化的差分运算有机组合而成,是目前最常用的拟合时间序列的模型。因为蝇密度数据具有明显的季节趋势等效应,为了更准确地描述这些效应的相互影响,需要采用其乘积季节模型:ARIMA(p,d,q)(P,D,Q)s。其中p、P表示模型的普通、季节自回归阶数,d、D分别表示普通、季节平稳化的差分阶数,q、Q表示普通、季节移动平均阶数,S代表季节的周期。
模型公式为:
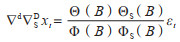
|
(1) |
式中:
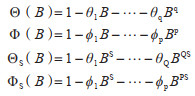
|
(2) |
θ表示移动平均系数,ϕ表示自回归系数。
1.3 模型预测与评价 1.3.1 建立数据库并选择预测模型2005-2022年长沙市蝇密度监测资料用Excel 2007软件按月份建立数据库,利用R 4.3.0软件进行分析,检验水准α=0.05。因蝇密度序列具有明显的季节性,故选择乘积季节性ARIMA模型对蝇密度数据进行建模。由于长沙市冬季寒冷,蝇密度极低,且历年监测未发现嗜寒性蝇种[8],故本研究将2005-2022年中未开展月份(1-3月、部分12月)的蝇密度取值为0。
1.3.2 建立ARIMA乘积季节模型的步骤 1.3.2.1 分析原始序列资料的变化趋势和特征建立ARIMA乘积季节模型,被处理数据的时间序列需处于平稳状态。为方便判断序列的平稳性,采用基于局部加权回归的时间序列分解法(seasonal-trend decomposition procedure based on Loess,STL)函数对数据进行分解,STL为时间序列分解中一种常见的算法,基于局部加权回归的方法将某时刻的数据分解为趋势分量、周期分量和余项。利用R 4.3.0软件绘制出原始序列分解图,通过分析序列随机性、季节性和长期趋势,判断是否达到平稳化要求。
1.3.2.2 序列的平稳化如序列有长期趋势或季节性趋势等特征,则为不平稳序列,应根据其特征,对其进行一般或季节性差分运算[9]。差分后进行单位根检验(augmented dickey-fuller test,ADF test)(α=0.05),以检验序列是否具有残留的长期趋势或季节性趋势,若P < 0.05则说明差分后的序列平稳。
1.3.2.3 参数判断通过自相关系数分析(autocorrelation function,ACF)图和偏自相关系数分析(partial autocorrelation function,PACF)图,可以大致选取乘积季节性模型ARIMA(p,d,q)(P,D,Q)s中参数p和P值,q及Q值,根据差分次数确定d和D值。由于该阶数过高会导致出现数据过度拟合的现象,因而一般取值不超过2[10]。然后采用最大似然估计对模型进行参数估计[11]。通过不断地调试比较,根据模型赤池信息准则(Akaike information criterion,AIC)值及贝叶斯信息准则(Bayesian information criterion,BIC)值来进行参数微调,AIC准则是建立在熵的概念基础上,常用于衡量统计模型拟合优良性的一种标准,BIC准则类似于AIC准则,但其参数相关的惩罚项更大,有助于避免过度拟合,AIC值及BIC值越小,模型越符合要求。
1.3.2.4 模型与参数的检验采用Box-Ljung显著性检验对模型进行诊断和检验,即在保证各参数均有统计学意义前提下,对模型残差序列进行白噪声检验,其自相关系数接近0,说明是白噪声序列,即所构建的最优模型提取了充分的原始序列信息,该模型对原始数据来说是最适宜的,否则需要重新选择参数建模。因R软件默认输出参数显著非零[12],所以本文未特意进行参数的显著性检验。
1.3.2.5 模型的预测效果评价利用2005年1月-2022年6月的蝇密度数据建立ARIMA模型,预测2022年7-12月蝇密度,同时用2022年下半年采集到的蝇密度真实数据与预测数据进行比较,进一步评价该模型的预测效果。
1.4 预测应用构建最优模型后,对长沙市2023年1-12月蝇密度进行预测。
2 结果 2.1 总体特征绘制2005年1月-2022年6月蝇密度监测数据的时间序列分解图,显示蝇密度季节效应较明显,且长期有降低趋势。见图 1。
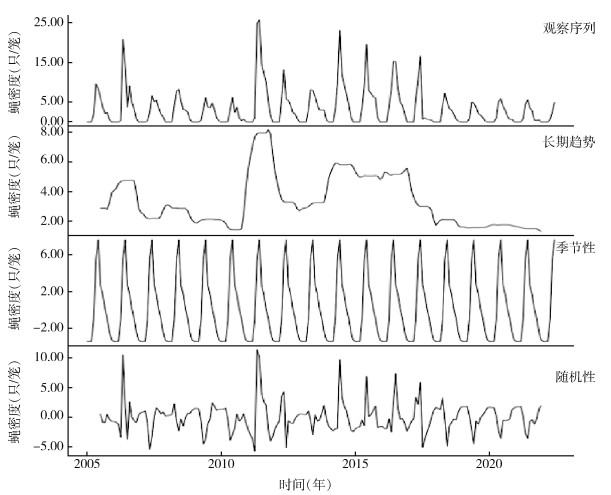
|
| 图 1 2005年1月-2022年6月长沙市蝇密度时间序列分解图 Figure 1 Time series decomposition of fly density in Changsha from January 2005 to June 2022 |
| |
蝇密度季节效应明显,对序列进行一次季节性差分,季节性差分后经ADF检验呈平稳序列,P=0.010,图形基本平稳(图 2)。对一次季节性差分后的序列进行Box-Ljung检验,χ2=242.230,P < 0.001,即该序列为显著非纯随机序列,可进一步建模。
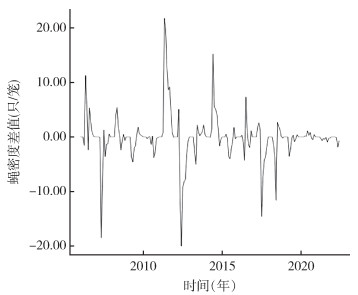
|
| 图 2 2005年1月-2022年6月长沙市蝇密度差值序列经一次季节性差分后的时间序列图 Figure 2 Time series after first-order seasonal difference of fly density in Changsha from January 2005 to June 2022 |
| |
将序列进行一次季节性差分后得到ACF、PACF图(图 3)。通过分析可以看出进行一次季节性差分后的时间序列依然表现出一定的周期性特点。根据ACF图和PACF图大致确定p、q、P、Q值,ACF图第1、12阶后截尾,Q值可取1或0,PACF图第1、12、24阶后截尾或拖尾,P值可取2、1或0;周期内ACF图可视为三阶截尾,q值可取2、1或0,PACF图可视为一阶截尾p值可取1或0。利用p、q、P、Q可能的参数组合分别建模,计算AIC值和BIC值。其中ARIMA(1,0,0)(0,1,1)12的AIC值(986.50)和BIC值(996.37)最小,为相对理想模型。
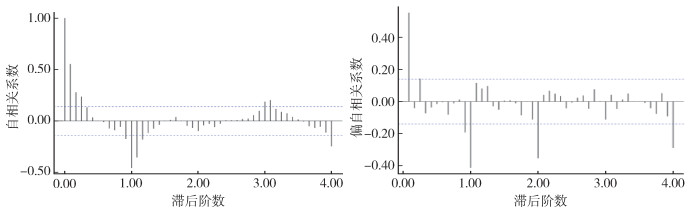
|
| 图 3 2005年1月-2022年6月长沙市蝇密度序列经一次季节性差分后自相关与偏自相关图 Figure 3 Autocorrelation and partial autocorrelation diagrams after first-order seasonal difference of fly density in Changsha from January 2005 to June 2022 |
| |
对ARIMA(1,0,0)(0,1,1)12模型残差进行Box-Ljung检验,滞后1阶到12阶的自相关系数检验P值为0.881、0.840、0.399、0.550、0.625、0.718、0.808、0.877、0.926、0.801、0.656、0.683,均 > 0.05,模型残差序列为白噪声序列,观察模型的残差ACF图,延迟阶数基本均未超出2倍标准差界限,残差自相关系数接近0(图 4)。模型自回归系数为0.577,季节性移动平均系数为-0.889。
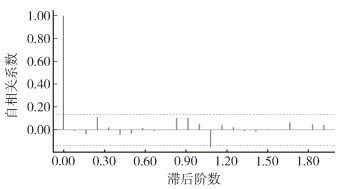
|
| 图 4 2005年1月-2022年6月长沙市蝇密度构建模型ARIMA(1,0,0)(0,1,1)12的残差自相关图 Figure 4 The residual autocorrelation diagram of the ARIMA(1, 0, 0)(0, 1, 1)12 model established on the fly density data in Changsha from January 2005 to June 2022 |
| |
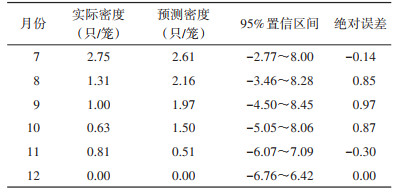
模型拟合曲线与实际值基本重合,实际监测值除个别超过了置信区间,基本都在区间内,模型对拟合期数据的拟合效果好(图 5)。模型均方根误差(root mean squared error,RMSE)为2.664,平均绝对误差(mean absolute error,MAE)为1.355。使用所建模型ARIMA(1,0,0)(0,1,1)12对2022年7-12月的蝇密度进行预测。将预测密度与实际监测密度进行比较,显示预测值与实际监测值基本吻合,实际值均落入了预测值的95%置信区间内(表 1),利用两者计算RMSE和MAE,RMSE=0.649,MAE=0.522。
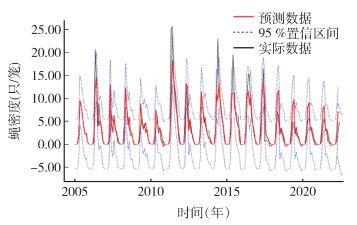
|
| 图 5 2005年1月-2022年6月长沙市蝇密度实际值、预测值及95%置信区间 Figure 5 Observed values, predicted values, and 95% confidence intervals of fly density in Changsha from January 2005 to June 2022 |
| |
|
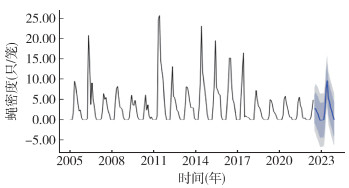
利用模型ARIMA(1,0,0)(0,1,1)12对2023年1-12月蝇密度进行预测,1-3月蝇密度取值为0,4-12月蝇密度预测结果分别为2.13、7.51、9.62、5.35、4.34、2.88、2.03、0.81和0.01只/笼。其中6月蝇密度最高,为9.62只/笼,12月份密度最低,为0.01只/笼。预测平均密度为2.89只/笼,低于2005-2022年历年平均密度(3.22只/笼),高于2022年平均密度(1.20只/笼),构建2023年度长沙市蝇密度的预测曲线,显示较2022年有增高趋势。见图 6。
|
| 注:深灰色区域为80%预测区间,浅灰色区域为95%预测区间。 图 6 2023年1-12月长沙市蝇密度的模型预测结果 Figure 6 Model prediction of fly density in Changsha from January to December 2023 |
| |
影响病媒生物密度变化的因素很多,如气象因素、生态环境、人口密度、卫生状况及国家卫生城市创建等,精准预测病媒密度变化趋势十分困难。国内外学者采用数学建模的方法对蚊虫及鼠类密度进行建模预测,效果较好。蝇类作为病媒生物的一种,采用数学建模的方法进行预测,具有一定可行性。时间序列分析研究的是某一事件在过去一段时间发生发展的规律,找到这种规律,并利用其预测未来一段时间内该事件的走向[13]。它把影响事物发生发展的各种因子综合在一个时间序列进行分析,不再区分不同的因素,不用花费大量时间和精力去收集影响因素数据,经济方便,应用前景广阔[14]。
影响蝇类密度的因素繁多,找到各种影响因素需要大量的人力物力,一些因素如人类活动、社会进程、爱国卫生工作情况及蝇类生态习性等很难获得,即便获得数据也难以总结并加入模型,如果放弃则会丢失数据,影响模型精度。这时,时间序列分析根据其自身规律来预测密度,是较为简单的方法[15]。ARIMA模型是时域分析模型中一个最重要和基本的模型,它综合了自回归模型和移动平均模型两者的作用,目前常被应用于传染病预测[16]。从序列分解图可看出,蝇密度变化与其他病媒生物一样,具有季节性和长期性等一些共同特点,ARIMA模型对其有很好的适用性。本研究构建的ARIMA(1,0,0)(0,1,1)12模型较好地拟合了既往蝇密度序列,残差序列通过了白噪声检验,说明模型对原始序列信息提取充分。预测的蝇密度趋势和实际数据基本一致,实际值除个别超过了置信区间,基本都在区间内,说明季节性ARIMA模型可以对蝇密度进行较好的短期预测。
模型预测结果显示,2023年蝇密度低于2005-2022年历年平均密度,但高于2022年平均密度,提示2023年长沙市应加大蝇密度控制力度,2023年密度高峰在6月,与往年相同,相关部门应在高峰来临之前的4、5月,采取有效的控制措施。此项研究可为长沙市蝇类风险评估指标的确定提供参考。例如,可以利用预测值95%置信区间设立警戒限值,当蝇密度超过限值时,说明蝇类危害事件发生及蝇传疾病传播的风险大,应采取相应措施,及时提醒相关医疗单位为相关媒介生物性传染病的暴发流行做好准备,作为制定病媒生物应急处置预案的参考依据,为启动预案限值的确定提供数据参考,或者应用于大型活动时蝇密度的控制[17]。多名学者提出模型预测数据可以应用于病媒生物防制措施效果评价[5, 7],同样,可以将蝇类监测数据与预测数据相比较,从而开展蝇类防制措施效果评价。
同时,应考虑ARIMA模型对蝇密度预测的局限性。当实际值与预测值有明显差异时,应结合实际进行分析[18]。乘积季节性ARIMA模型更适合短期预测,探索乘积季节性ARIMA模型结合影响因素,或与其他模型相组合,并不断引入新的数据,不断修正模型,是下一步长沙市蝇密度预测研究的一个方向。
利益冲突 无
| [1] |
苏畅, 林敏珍. 厦门市2014年苍蝇密度监测资料分析[J]. 中国热带医学, 2016, 16(1): 95-96. Su C, Lin MZ. Population surveillance of filth fly in Xiamen city in 2014[J]. China Trop Med, 2016, 16(1): 95-96. DOI:10.13604/j.cnki.46-1064/r.2016.01.27 |
| [2] |
中华人民共和国卫生部. 全国病媒生物监测方案(试行)[Z]. 北京: 中国疾病预防控制中心, 2005. Ministry of Health of the People's Republic of China. National vector surveillance program(Trial)[Z]. Beijing: Chinese Center for Disease Control and Prevention, 2005. (in Chinese) |
| [3] |
Zhu ZX, Zhu XX, Zhan YC, et al. Development and comparison of predictive models for sexually transmitted diseases-AIDS, gonorrhea, and syphilis in China, 2011-2021[J]. Front Public Health, 2022, 10: 966813. DOI:10.3389/fpubh.2022.966813 |
| [4] |
Siamba S, Otieno S, Koech J. Application of ARIMA, and hybrid ARIMA models in predicting and forecasting tuberculosis incidences among children in Homa bay and Turkana counties, Kenya[J]. PLoS Digital Health, 2023, 2(2): e0000084. DOI:10.1371/journal.pdig.0000084 |
| [5] |
潘衍宇, 吴海霞, 国佳, 等. 基于R语言自回归积分移动平均模型的广州市白纹伊蚊密度预测研究[J]. 中国媒介生物学及控制杂志, 2018, 29(6): 545-549. Pan YY, Wu HX, Guo J, et al. Population density prediction of Adeds albopictus in Guangzhou based on autoregressive integrated moving average model[J]. Chin J Vector Biol Control, 2018, 29(6): 545-549. DOI:10.11853/j.issn.1003.8280.2018.06.001 |
| [6] |
高文, 黄钢, 韩晓莉. 基于蚊密度差分自回归移动平均模型预测流行性乙型脑炎的贝叶斯判别分析研究[J]. 中国媒介生物学及控制杂志, 2018, 29(6): 557-563. Gao W, Huang G, Han XL. Application of Bayes analysis in Japanese encephalitis prediction based on multiple seasonal autoregressive integrated moving average model[J]. Chin J Vector Biol Control, 2018, 29(6): 557-563. DOI:10.11853/j.issn.1003.8280.2018.06.003 |
| [7] |
孙钦同, 韩英男, 刘言, 等. 应用自回归移动平均(ARIMA)模型预测山东省鼠密度趋势[J]. 中国媒介生物学及控制杂志, 2021, 32(6): 744-748. Sun QT, Han YN, Liu Y, et al. Application of autoregressive integrated moving average model in predicting the trend of rodent density in Shandong province, China[J]. Chin J Vector Biol Control, 2021, 32(6): 744-748. DOI:10.11853/j.issn.1003.8280.2021.06.018 |
| [8] |
彭莱, 何俊, 肖珊, 等. 长沙市2006-2015年蝇类密度监测结果分析[J]. 中国媒介生物学及控制杂志, 2017, 28(5): 496-498. Peng L, He J, Xiao S, et al. Analysis on the fly density monitoring in Changsha city from 2006 to 2015[J]. Chin J Vector Biol Control, 2017, 28(5): 496-498. DOI:10.11853/j.issn.1003.8280.2017.05.024 |
| [9] |
布洛克威尔, 田铮. 时间序列的理论与方法[M]. 北京: 高等教育出版社, 2001: 214-246. Brockwell, Tian Z. Time series: Theory and methods[M]. Beijing: Higher Education Press, 2001: 214-246. |
| [10] |
毛向群, 熊小庆, 涂秋凤, 等. 江西省乙型肝炎发病趋势的时间序列和预测模型分析[J]. 中国预防医学杂志, 2013, 14(6): 435-438. Mao XQ, Xiong XQ, Tu QF, et al. Analysis on the time series and prediction model in forecasting the incidence of hepatitis B in Jiangxi[J]. Chin Prev Med, 2013, 14(6): 435-438. DOI:10.16506/j.1009-6639.2013.06.012 |
| [11] |
王丙刚, 曲波, 郭海强, 等. 传染病预测的数学模型研究[J]. 中国卫生统计, 2007, 24(5): 536-540. Wang BG, Qu B, Guo HQ, et al. Research on mathematical models for predicting infectious diseases[J]. Chin J Health Stat, 2007, 24(5): 536-540. |
| [12] |
王燕. 应用时间序列分析: 基于R[M]. 北京: 中国人民大学出版社, 2015: 83-106. Wang Y. Time series analysis with R[M]. Beijing: China Renmin University Press, 2015: 83-106. |
| [13] |
易丹辉, 王燕. 应用时间序列分析[M]. 5版. 北京: 中国人民大学出版社, 2019: 2-3. Yi DH, Wang Y. Applied time series analysis[M]. 5th ed. Beijing: China Renmin University Press, 2019: 2-3. |
| [14] |
沈钰刚. 嵊州市流感样病例监测结果及ARIMA模型预测[D]. 杭州: 浙江大学, 2017: 20-24. Shen YG. Analysis of influenza surveillance results in Shengzhou and ARIMA model prediction[D]. Hangzhou: Zhejiang University, 2017: 20-24. (in Chinese) |
| [15] |
张顺先, 邱琪, 王英. 我国手足口病重症患者数自回归移动平均模型预测研究[J]. 病毒学报, 2017, 33(1): 77-81. Zhang SX, Qiu Q, Wang Y. Study on the national monthly reported severe cases of hand-foot-mouth disease forecasted by autoregressive integrated moving average model[J]. Chin J Virol, 2017, 33(1): 77-81. DOI:10.13242/j.cnki.bingduxuebao.003097 |
| [16] |
王伶, 姚文清. 利用时间序列模型分析预测辽宁手足口病疫情趋势[J]. 中国卫生统计, 2016, 33(5): 847-849. Wang L, Yao WQ. Using time series models to analyze and predict the epidemic trend of hand-foot-mouth disease in Liaoning[J]. Chin J Health Stat, 2016, 33(5): 847-849. |
| [17] |
运玲, 王福才, 张秋芬. 差分自回归移动平均模型在蚊密度分布特征预测中的应用[J]. 中国媒介生物学及控制杂志, 2020, 31(1): 21-26. Yun L, Wang FC, Zhang QF. Application of autoregressive integrated moving average model in prediction of the distribution characteristics of mosquito density in Tangshan, Hebei province, China[J]. Chin J Vector Biol Control, 2020, 31(1): 21-26. DOI:10.11853/j.issn.1003.8280.2020.01.005 |
| [18] |
孙彩云, 杨晓静. 乘积ARIMA模型的建立及应用[J]. 华北科技学院学报, 2008, 5(2): 85-89. Sun CY, Yang XJ. Establish and application of multiply ARIMA model[J]. J North China Inst Sci Technol, 2008, 5(2): 85-89. DOI:10.3969/j.issn.1672-7169.2008.02.025 |
 2023, Vol. 34
2023, Vol. 34

