扩展功能
文章信息
- 刘天, 姚梦雷, 侯清波, 黄继贵, 吴杨, 杨瑞, 陈红缨
- LIU Tian, YAO Meng-lei, HOU Qing-bo, HUANG Ji-gui, WU Yang, YANG Rui, CHEN Hong-ying
- 7种时间序列模型对全国肾综合征出血热发病率预测效果比较
- Comparison of seven time series models in fitting and predicting the incidence of hemorrhagic fever with renal syndrome in China
- 中国媒介生物学及控制杂志, 2022, 33(4): 548-554
- Chin J Vector Biol & Control, 2022, 33(4): 548-554
- 10.11853/j.issn.1003.8280.2022.04.020
-
文章历史
- 收稿日期: 2022-04-11
2 湖北省疾病预防控制中心, 湖北 武汉 430079
2 Hubei Center for Disease Control and Prevention, Wuhan, Hubei 430079, China
国家传染病自动预警信息系统于2008年成功实施并开始在全国范围内运行[1-2]。该系统的诞生标志着我国拥有了自动化、数字化的疾病预警实时应用工具。它有助于在县、市级层面及早发现疫情,并向省级、国家级疾病预防控制中心(CDC)报告可能的暴发疫情,真正实现了暴发疫情的早发现策略[2]。但经过近10年的运行,该系统也暴露出阳性率低、预警特异度差的问题[3-5]。该系统时间序列预警采用固定阈值法和移动百分位数法(MPM)[6],2种方法虽易于理解,原理简单,但对复杂的疾病时间序列拟合及预测效果差。近些年,不少学者将复杂的时间序列模型,如乘积季节自回归移动平均模型(SARIMA)[7-8]、指数平滑模型(ETS)[8]以及神经网络模型[9-11]等应用于疾病的预测、预警,拟合及预测效果较好。肾综合征出血热(HFRS)在我国属法定乙类传染病,是我国重要的自然疫源性疾病之一,21世纪以来该病整体呈下降趋势,但在局部常常出现暴发[12-13]。目前传染病自动预警系统采用移动百分位数法对HFRS进行预警,预警特异度差。因此有必要对预警模型进行优化,提高模型预测、预警精度。本研究选择7种最常见时间序列预测预警模型,对全国HFRS发病率进行拟合及预测,评价拟合及预测效果,为优化HFRS预警模型提供参考。
1 材料与方法 1.1 资料来源资料来源于公共卫生科学数据中心(http://www.phsciencedata.cn/)。收集2004-2017年全国HFRS逐月发病率资料。以2004年1月-2017年6月全国HFRS发病率数据作为训练数据,训练模型并预测2017年7-12月发病率;以2017年7-12月全国HFRS发病率数据作为测试数据。比较拟合值与训练数据、预测值与测试数据,评价模型拟合及预测效果。
1.2 方法本研究选择7个常用时间序列模型,包括:SARIMA、ETS、时间序列线性模型(TSLM)、自回归神经网络模型(NNAR)、指数平滑空间状态模型(TBATS)、时间序列3次样条平滑模型(TSSPLINE)和时间序列广义回归模型(TSGRNN)。其中,SARIMA、ETS、TSLM、TSSPLINE属于单一时间序列模型;NNAR、TSGRNN属于神经网络模型;TBATS属于时间序列组合模型。
1.2.1 SARIM模型SARIM模型一般形式为:SARIMA(p,d,q)(P,D,Q)s。其中,d、D分别表示一般差分、季节性差分阶数,p、q表示自回归阶数、移动平均阶数,P、Q表示季节性自回归阶数和季节性移动平均阶数,s表示季节周期长度,存在明显季节性的疾病监测月数据,一般取12。建模的关键在于确定上述参数,上述参数取值一般不超过5[14]。本研究将p、q、P、Q最大值设为5,d、D最大值设为2,采取逐步测试方法,利用最小赤池信息量准则(AIC)原则筛选最优模型[14]。利用Box-Ljung Q检验最优模型残差是否为白噪声序列。
1.2.2 ETS模型可分为1、2、3次指数平滑模型,4个参数分别为水平分量(α)、趋势分量(β,ϕ)和季节分量(γ)[15]。在实际应用中,根据数据的趋势性、季节性特点,结合模型拟合优度[如对数似然比(LLR)]等指标选择最优模型。在R中利用ets()函数自动建模,筛选最优模型,筛选指标选择LLR[15]。
1.2.3 TSLM模型基本思想是认为时间序列可分解为趋势项和季节项,因此建立线性回归模型::y =α*trend + β*season + Intercept。其中,trend为月份序号,2004年1月、2004年2月…… 2017年12月依次取值1、2…… 168;season根据季节性特点进行设置哑变量,如月份数据,则设置11个哑变量,均与1月相比较;α、β分别为趋势项参数和季节性系列参数;Intercept为常数项。在R中利用tslm()函数建立模型。
1.2.4 NNAR模型考虑时间序列长期趋势、季节性特征,利用自回归模型(AR)自动定阶确定自回归阶数(p),以滞后p阶数据、季节性滞后1或2阶数据作为输入,实际值作为输出拟合前馈型神经网络。在R中利用nnetar()函数建立NNAR模型[14]。通过Box-Ljung Q检验残差是否为白噪声序列。为消除初始值设置影响模型稳定性,建立20个神经网络,取多个神经网络拟合值、预测值均值作为模型最终拟合值、预测值。
1.2.5 TBATS模型“TBATS”是融合傅里叶三角(trigonometric)、Box-Cox变换(Box-Cox transformation)、ARMA残差(ARMA errors)、趋势(trend)和季节性成分(seasonal components)的指数平滑空间状态模型,是一种复杂的时间序列组合模型[16]。该模型参数众多,在R中利用tbats()函数,根据AIC最小的原则完全自动化的确定各参数值,以拟合TBATS模型。
1.2.6 TSSPLINE模型该方法基于随机状态空间模型,是ARIMA(0,2,2)模型的一个特例,它为平滑参数提供了一个简单的上限,以确保可逆模型。这种方法相对于完整的ARIMA(0,2,2)模型的优势在于它提供了平滑的趋势估计以及线性预测函数[17]。在R中利用splinef()函数构建模型并预测。
1.2.7 TSGRNN模型该方法实际基于广义回归神经网络(GRNN),对于存在明显季节性的数据以1∶m阶滞后数据作为输入(m为季节性长度),当月数据作为输出,建立GRNN模型。采用滚动原点技术(rolling origin technique)探寻GRNN模型最优参数δ[18],可以快速地单次学习并产生确定性的结果。在R中利用grnn_forecasting()函数建立模型。
1.3 统计学分析及模型评价利用R 4.0.1软件“tseries”“forecast”“tsfgrnn”包整理数据和模型建立,绘图利用“ggplot2”包。ts()函数用于建立时间序列,mstl()函数用于季节分解,forecast()函数用于预测,checkresiduals()函数用于Box-Ljung Q检验。所有参数最小值设为模型拟合及预测效果评价,采用平均绝对误差百分比(mean absolute percentage error,MAPE)、平均绝对误差(mean absolute error,MAE)、均数标准差(root mean squared error,RMSE)和平均误差率(mean error rate,MER)4个指标;选取拟合及预测评价指标均据前3位、拟合及预测效果据前列且较均衡者为最优模型。检验水准α=0.05。
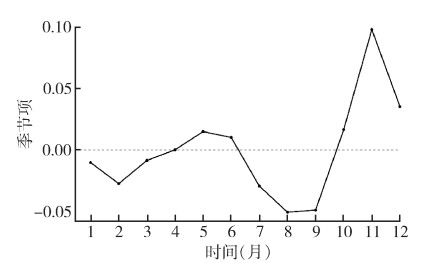
2 结果 2.1 一般概况2004-2017年全国累计报告HFRS 178 237例,死亡1 753例,年平均发病率为0.95/10万,死亡率为0.009/10万,病死率为0.98%。季节分析结果显示,全国HFRS疫情整体呈下降趋势,其中2004年1月-2010年1月整体呈下降趋势;随后整体呈上升趋势,至2013年1月达到顶峰后下降。2017年10-12月有所上升。全国HFRS存在明显季节性,呈双峰分布。第1个高峰出现在5-6月,第2个高峰出现在10-12月,第2高峰明显高于第1高峰。见图 1、2。

|
| 图 1 2004-2017年全国肾综合征出血热发病率时间序列分解 Figure 1 Decomposition of time series of national incidence of hemorrhagic fever with renal syndrome from 2004 to 2017 |
| |
|
| 图 2 2004-2017年全国肾综合征出血热发病率时间序列的月份分布 Figure 2 Monthly distribution of time series of national incidence of hemorrhagic fever with renal syndrome from 2004 to 2017 |
| |
利用auto.arima()函数自动拟合模型,得到最优模型为SARIMA(0,1,4)(2,1,1)[12]。R2=0.94,AIC=-851.65,Box-Ljung Q=12.20,P=0.788,残差为白噪声。拟合MAPE=11.46%。拟合效果见表 1;残差围绕0均匀分布。见图 3。
|

|
| 图 3 乘积季节自回归移动平均模型(SARIMA)等6种模型拟合肾综合征出血热发病率的残差分布 Figure 3 Residual distributions from fitting incidence of hemorrhagic fever with renal syndrome by six time series models including the seasonal autoregressive integrated moving average model (SARIMA) |
| |
最终3次指数平滑模型为最优模型,季节、残差成分为相乘模式,趋势成分为相加模式。其中α=0.83,β=0.003,ϕ=0.98,γ=1.0×10-4,LLR=350.18,AIC=-664.35。拟合MAPE=10.25%。拟合效果见表 1;残差围绕0均匀分布。见图 3。
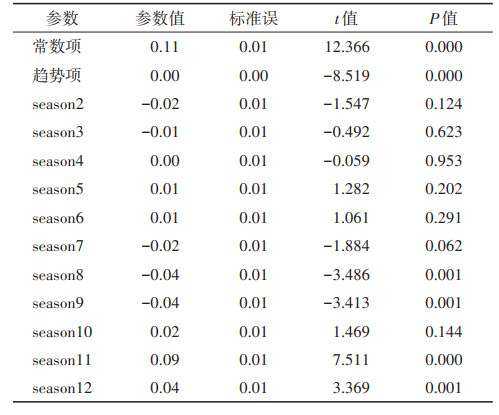
2.4 TSLM模型建立最终模型R2=0.64,建立线性模型差异有统计学意义(F=21.928,P < 0.001)。参数检验见表 2,其中常数项参数为0.11(t=12.366,P < 0.001)、趋势项参数为-4.33×10-4(t=-8.519,P < 0.001),差异均有统计学意义。季节项中的season8、season9、season11、season12哑变量差异亦有统计学意义(均P < 0.05)。拟合MAPE=33.91%。拟合效果见表 1;残差分布不均,见图 3。
|
NNAR(16,1,8)[12]为最优模型,建立16-8-1的神经网络模型,共145个权重值。Box-Ljung Q=8.35,P=0.400,残差为白噪声。拟合MAPE=1.84%。拟合效果见表 1;残差围绕0均匀分布。见图 3。
2.6 TBATS模型建立利用tbats()函数自动建立模型,得到模型参数λ=2.71×10-4,α=1.053,p=0,q=0,γ1=-7.07×10-3,γ2=5.42×10-3,疾病数据仅有1个季节周期,季节周期长度mi=12,傅里叶级数ki=5,模型AIC=-708.44,LLR=-738.44。拟合效果见表 1;残差围绕0均匀分布。见图 3。
2.7 TSSPLINE和TSGRNN模型建立利用splinef()函数建立TSSPLINE模型,拟合MAPE=10.82%。利用grnn_forecasting()函数建立TSGRNN模型,sigma参数设为“ROLLING”,逐步预测法选择迭代法(recursive),控制长期趋势选择相加模式(additive)。为评价拟合效果,利用滚动原点技术[rolling_origin()函数]获取拟合值与预测值,结果显示MAPE=22.29%。拟合效果见表 1;TSSPLINE模型残差分布均匀(图 3);TSGRNN残差图、拟合图无法给出。
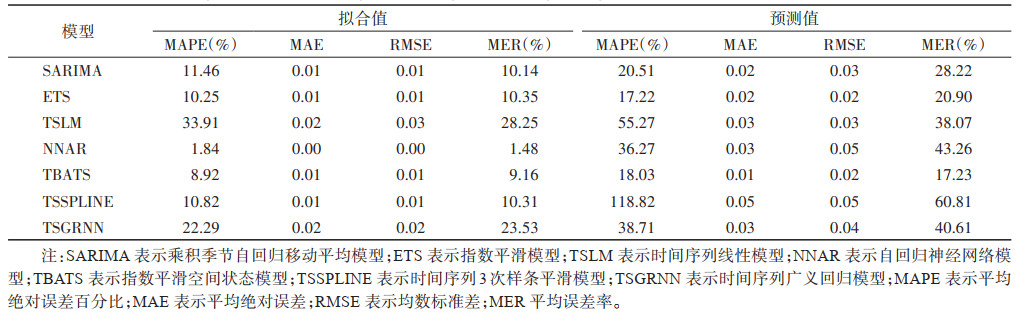
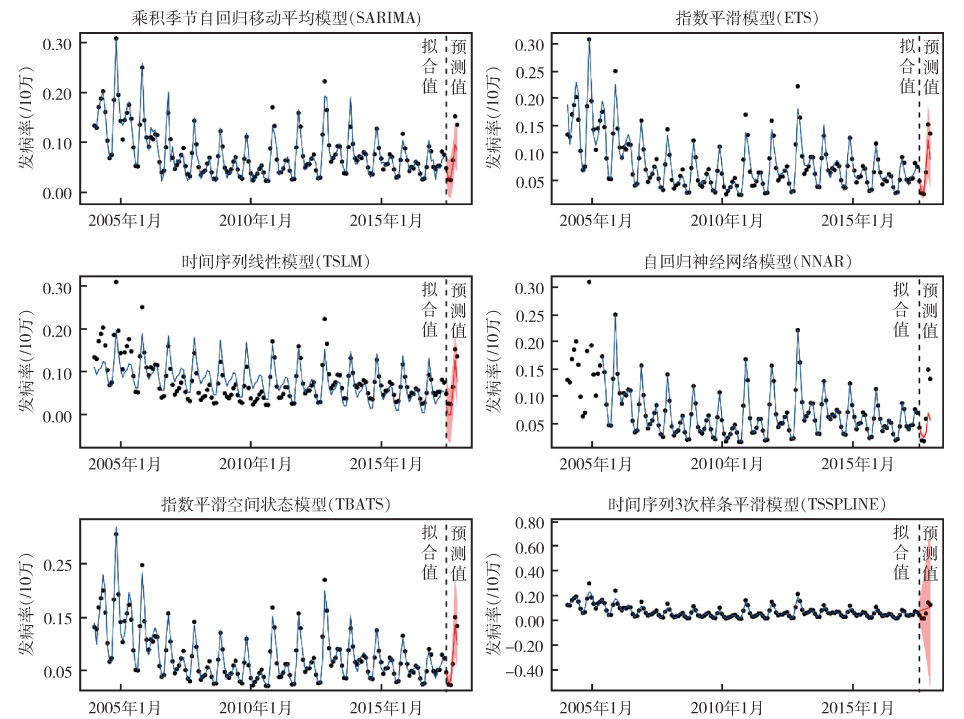
2.8 拟合及预测效果比较从MAPE来看,拟合效果从高到底依次为:NNAR > TBATS > ETS > TSSPLINE > SARIMA > TSGRNN > TSLM;预测效果从高到底依次为:ETS > TBATS > SARIMA > NNAR > TSGRNN > TSLM > TSSPLINE。MAE、RMSE指标拟合效果排序与MAPE基本一致;SARIMA模型的MER指标优于ETS、TSSPLINE模型。MAE、RMSE、MER指标预测效果TBATS模型优于ETS模型。综合拟合及预测效果来看,TBATS为最优模型,其次为ETS模型。TSLM、TSSPLINE模型拟合及预测效果差,不适于HFRS模型拟合及预测。不同模型拟合及预测效果见表 1、图 4。
|
| 图 4 乘积季节自回归移动平均模型(SARIMA)等6种模型拟合值及预测值与实际值比较 Figure 4 Comparison of fitted and predicted values with actual values for six time series models |
| |
MPM是以前3年或5年同期及前后各摆动2个单位,取历史15个数据或25个数据的中位数作为当期预测值,以第60~90百分位数值作为预警值。当数据较平稳,不存在明显长期趋势变化时,该方法表现较好。监测结果显示,全国HFRS发病率呈逐年下降趋势。若利用MPM预警未来趋势,将会导致预警阈值设置过高,灵敏度较差等问题。这是因为MPM未考虑序列的长期趋势变化,该方法不适于存在明显长期趋势疾病的预测、预警。本研究以2004-2017年全国HFRS发病率数据为例,比较了常见7种时间序列模型的拟合及预测效果。结果显示,TBATS、ETS和SARIMA 3种模型在HFRS拟合及预测中的表现较好,拟合及预测MAPE均低于20%,模型拟合及预测精度属于优秀;其中TBATS为最优模型,拟合及预测精度均较高。NNAR、TSGRNN 2种神经网络模型在HFRS拟合中表现很好,尤其是NNAR模型,拟合精度高,但预测精度较差。提示2个神经网络模型可能存在过拟合,导致模型泛化能力差。这与既往研究报道不一致[9-10, 19-20],提示神经网络模型拟合及预测效果不一定优于非神经网络模型,在实际应用过程中还应结合疾病特征,择优选择。TSLM、TSSPLINE模型在全国HFRS拟合及预测中表现较差,不适于HFRS的预测、预警。另外,模型建立成功与否除了能预测HFRS发病率外,还应具备预测其置信区间的能力。7种方法中,TSGRNN模型无法预测置信区间,其他6种方法均能得到置信区间,可以进行监测预警。TSGRNN模型不适于疾病监测预警。
理想的预测模型应是拟合及预测效果均较好的模型,但在实际工作中较少获得。在选取最优模型中,由于缺乏客观统一标准,作者提出拟合及预测评价指标均居前3位、拟合及预测效果居前列且较均衡者为最优模型的标准,综合考虑了拟合及预测效果,用于筛选最优模型,具有一定参考意义。本文中,TBATS为最优模型,拟合及预测精度均较高,与既往手足口病研究结果一致[21]。该模型是傅里叶三角、Box-Cox变换、ARIMA残差和指数平滑组成的组合模型。其各个组件有机地、连贯地组合在一起以拟合时间序列数据,TBATS模型的机制在数学上很复杂,已被证明结果稳定且适用于时间序列数据。该模型尤其是对长期数据,如疾病季节模式发生变化的时间序列,能很好地拟合多个季节模式,这是明显区别于其他时间序列模型最大的优点。另外,该模型作为组合模型,综合了ARIMA、ETS模型结合傅里叶三角对季节性提取的优点,拟合及预测精度较高。该模型于2011年提出,在疾病监测领域应用较少,今后值得进一步推广使用,以探讨该模型的普适性。另外,上述模型均封装在R软件“forecast”包中,各类预测模型原理复杂,但笔者将各种方法高度函数化,通过简单编程即能实现建模预测、预警。
综上所述,TBATS模型为全国HFRS预测、预警的最优模型,值得进一步推广应用。本研究也存在一定的局限性:首先,本研究仅选取常见的7种时间序列模型,未纳入更多模型,HFRS最优模型可能未被纳入分析模型;其次,数据仅选取2004-2017年数据,未能获取2018-2020年数据,数据的选取可能对模型拟合及预测效果有影响。今后将利用不同长度、不同维度(包括省、直辖市、自治区)数据进行建模,以评价TBATS模型的稳定性,进一步优化HFRS预警模型。
利益冲突 无
| [1] |
Zhang HL, Wang LP, Lai SJ, et al. Surveillance and early warning systems of infectious disease in China: From 2012 to 2014[J]. Int J Health Plann Manage, 2017, 32(3): 329-338. DOI:10.1002/hpm.2434 |
| [2] |
Yang WZ, Li ZJ, Lan YJ, et al. A nationwide web-based automated system for early outbreak detection and rapid response in China[J]. Western Pac Surveill Response J, 2011, 2(1): 10-15. DOI:10.5365/WPSAR.2010.1.1.009 |
| [3] |
方艳, 宋铁, 李灵辉, 等. 广东省传染病自动预警系统运行现状分析[J]. 中华流行病学杂志, 2013, 34(8): 800-803. Fang Y, Song T, Li LH, et al. Current situation on the China Infectious Disease Automated-alert and Response System in Guangdong province, China[J]. Chin J Epidemiol, 2013, 34(8): 800-803. DOI:10.3760/cma.j.issn.0254-6450.2013.08.011 |
| [4] |
吕炜, 赖圣杰, 唐忠, 等. 广西壮族自治区2009-2011年传染病自动预警系统运行效果分析[J]. 中华流行病学杂志, 2013, 34(6): 589-593. Lyu W, Lai SJ, Tang Z, et al. Application of the China Infectious Diseases Automated-alert and Response System in Guangxi, 2009-2011[J]. Chin J Epidemiol, 2013, 34(6): 589-593. DOI:10.3760/cma.j.issn.0254-6450.2013.06.012 |
| [5] |
徐旭卿, 鲁琴宝, 王臻, 等. 浙江省传染病自动预警系统暴发预警效果评价[J]. 中华流行病学杂志, 2011, 32(5): 442-445. Xu XQ, Lu QB, Wang Z, et al. Evaluation on the performance of China Infectious Disease Automated-alert and Response System(CIDARS)in Zhejiang province[J]. Chin J Epidemiol, 2011, 32(5): 442-445. DOI:10.3760/cma.j.issn.0254-6450.2011.05.004 |
| [6] |
Kuang J, Yang WZ, Zhou DL, et al. Epidemic features affecting the performance of outbreak detection algorithms[J]. BMC Public Health, 2012, 12: 418. DOI:10.1186/1471-2458-12-418 |
| [7] |
Ceylan Z. Estimation of COVID-19 prevalence in Italy, Spain, and France[J]. Sci Total Environ, 2020, 729: 138817. DOI:10.1016/j.scitotenv.2020.138817 |
| [8] |
Liu H, Li CX, Shao YQ, et al. Forecast of the trend in incidence of acute hemorrhagic conjunctivitis in China from 2011-2019 using the seasonal autoregressive integrated moving average (SARIMA) and exponential smoothing (ETS) models[J]. J Infect Public Health, 2020, 13(2): 287-294. DOI:10.1016/j.jiph.2019.12.008 |
| [9] |
Zhai MM, Li WH, Tie P, et al. Research on the predictive effect of a combined model of ARIMA and neural networks on human brucellosis in Shanxi province, China: A time series predictive analysis[J]. BMC Infect Dis, 2021, 21(1): 280. DOI:10.1186/s12879-021-05973-4 |
| [10] |
Wu W, An SY, Guan P, et al. Time series analysis of human brucellosis in mainland China by using Elman and Jordan recurrent neural networks[J]. BMC Infect Dis, 2019, 19(1): 414. DOI:10.1186/s12879-019-4028-x |
| [11] |
Li ZQ, Pan HQ, Liu Q, et al. Comparing the performance of time series models with or without meteorological factors in predicting incident pulmonary tuberculosis in eastern China[J]. Infect Dis Poverty, 2020, 9(1): 151. DOI:10.1186/s40249-020-00771-7 |
| [12] |
刘建, 闫佳, 夏军林. 某县一起流行性出血热暴发疫情的调查分析[J]. 河南预防医学杂志, 2020, 31(1): 63-65. Liu J, Yan J, Xia JL. Investigation and analysis of an outbreak of epidemic hemorrhagic fever in a county[J]. Henan J Prev Med, 2020, 31(1): 63-65. DOI:10.13515/j.cnki.hnjpm.1006-8414.2020.01.019 |
| [13] |
刘淑萍. 一起野外施工流行性出血热暴发流行病学分析[J]. 中国公共卫生管理, 2011, 27(1): 60-61. Liu SP. Epidemiological analysis of an outbreak of epidemic hemorrhagic fever in field construction[J]. Chin J Public Health Mange, 2011, 27(1): 60-61. DOI:10.19568/j.cnki.23-1318.2011.01.034 |
| [14] |
Hyndman RJ, Khandakar Y. Automatic time series forecasting: The forecast package for R[J]. J Stat Softw, 2008, 27(3): 1-22. DOI:10.18637/jss.v027.i03 |
| [15] |
Hyndman RJ, Koehler AB, Snyder RD, et al. A state space framework for automatic forecasting using exponential smoothing methods[J]. Int J Forecasting, 2002, 18(3): 439-454. DOI:10.1016/S0169-2070(01)00110-8 |
| [16] |
De Livera AM, Hyndman RJ, Snyder RD. Forecasting time series with complex seasonal patterns using exponential smoothing[J]. J Am Stat Assoc, 2011, 106(496): 1513-1527. DOI:10.1198/jasa.2011.tm09771 |
| [17] |
Hyndman RJ, King ML, Pitrun I, et al. Local linear forecasts using cubic smoothing splines[J]. Aust N Z J Stat, 2005, 47(1): 87-99. DOI:10.1111/j.1467-842X.2005.00374.x |
| [18] |
Martínez F, Charte F, Rivera AJ, et al. Automatic time series forecasting with GRNN: A comparison with other models[C]//Proceedings of the 15th International Work-Conference on Advances in Computational Intelligence. Gran Canaria: Springer, 2019: 198-209. DOI: 10.1007/978-3-030-20521-8_17.
|
| [19] |
Guo YH, Feng Y, Qu FL, et al. Prediction of hepatitis E using machine learning models[J]. PLoS One, 2020, 15(9): e0237750. DOI:10.1371/journal.pone.0237750 |
| [20] |
Wang YW, Shen ZZ, Jiang Y. Comparison of autoregressive integrated moving average model and generalised regression neural network model for prediction of haemorrhagic fever with renal syndrome in China: A time-series study[J]. BMJ Open, 2019, 9(6): e025773. DOI:10.1136/bmjopen-2018-025773 |
| [21] |
Yu CC, Xu CJ, Li YH, et al. Time series analysis and forecasting of the hand-foot-mouth disease morbidity in China using an advanced exponential smoothing state space TBATS model[J]. Infect Drug Resist, 2021, 14: 2809-2821. DOI:10.2147/IDR.S304652 |
 2022, Vol. 33
2022, Vol. 33


