蚊媒传染病是我国重要的传染病之一^[1]，其中淡色库蚊（Culex pipiens pallens）/致倦库蚊（Cx. pipiens quinquefasciatus）是我国分布最广、危害最大的蚊种之一^[2]，对我国公共卫生安全有重要影响。监测和控制淡色库蚊密度是预防和控制以淡色库蚊为媒介的传染病最有效的方法^[3]。

淡色库蚊的密度监测旨在通过连续、系统、科学地收集淡色库蚊的数量信息，进行数据分析，为病媒生物控制策略和措施提供依据（《全国病媒生物监测实施方案》（中疾控传防发〔2016〕56号）。在监测过程中监测频次的设置具有十分重要的意义，监测频次过高可能2次监测间的密度差异无统计学意义导致资源的浪费，监测频次过低则会无法准确掌握蚊密度的时间变化信息。然而，目前缺乏蚊虫监测频次方面的研究，因此我们将之前建立的泰勒幂方程^[4]代入两样本均数比较的样本量公式^[5]，并用线性回归^[6]拟合影响淡色库蚊密度的最重要的气象因素——平均气温^[7]与蚊密度的关系，建立基于温度差的抽样模型，可以在给定u_α和u_β水平下，计算某样本量下能辨别的最小均数差值δ所对应的最小温度差异∆T。从而根据平均气温变化推算更高效的监测频次。使监测频次，既不会过高使2次监测间的蚊密度差异无统计学意义，也不会过低而无法准确掌握蚊密度的时间变化信息，为确定CO₂诱蚊灯法监测淡色库蚊密度的频次提供理论依据。

在上海市除崇明区外的15个区，共设置229个CO₂诱蚊灯监测点。各区分别选择医院、农户、牲畜棚（如有）各2处作为监测点，其余按照城镇居民区、公园（含街心公园）、学校等场所平均分配。除牲畜棚外，其余监测点在外环境进行，每个监测点设置1个CO₂诱蚊灯。于2019和2020年的4－11月每旬监测1次，监测时间为16：00－22：00，遇雨天、风力 > 5级顺延1 d开展监测。捕获的蚊虫收集至实验室，在体视镜下分类鉴定并计数，计算蚊密度。

本次研究选用的CO₂诱蚊灯由上海禾奇科学仪器有限公司生产，引诱方式为：CO₂气体（4 L气瓶）、光源和诱饵。

本次研究使用上海市2019年CO₂诱蚊灯法监测数据拟合模型，并使用2020年CO₂诱蚊灯法监测数据验证。

(1)

其中，a、b为2个非负参数，a是与抽样等因素有关的参数，b是反映物种聚集特征的参数。x为每旬监测的229个CO₂诱蚊灯样本的平均蚊密度，s²为其方差。泰勒幂方程参数由上海市2019年CO₂诱蚊灯法监测数据拟合^[4]。

所采用的两样本均数比较的样本量估算公式^[5]如下：

(2)

其中，n为样本量，σ为总体标准差（由样本标准差s代替），密度差值δ=|μ₁-μ₂|，为两样本均数的差值，u_α和u_β分别为检验水准α（取双侧）和Ⅱ型错误概率（取单侧）所对应的u值。

将（1）带入公式（2）得：

(3)

其中，a、b、x、α、u_α和u_β等参数意义与公式（1）、（2）相同。

由公式（3）整理得基于密度差的抽样模型：

(4)

其中，a、b、x、α、u_α和u_β等参数意义与公式（1）、（2）相同。

公式（4）可由x在给定u_α和u_β水平下，计算某样本量下能辨别的最小均数差值δ。

将淡色库蚊2次CO₂诱蚊灯监测的密度差值δ与该2次监测前1旬的平均气温的差值∆T使用线性回归模型拟合。

(5)

其中，δ为淡色库蚊2次CO₂诱蚊灯监测的密度差值，∆T为该2次监测时的前1旬平均气温的差值，β₁和β₀为回归参数。

公式（5）代入公式（4）得基于温度差的抽样模型：

(6)

公式（6）可由x在给定u_α和u_β水平下，计算某样本量下能辨别的最小均数差值δ所对应的最小温度差值∆T，以此推算最佳的监测频次。使监测频次既不会过高而导致2次监测间的蚊密度差异无统计学意义，也不会过低而无法准确掌握蚊密度的时间变化信息。

以准确率、召回率和调和平均值（F-measure）验证模型拟合效果^[8]。

F-measure最大值为1，最小值为0。在最佳状态下，准确率和召回率均为1，此时调和平均值为1。

气象数据来源于中国国家气象科学数据中心。

采用Excel 2010软件进行数据录入和整理，SPSS 20.0软件进行统计分析。使用2个独立样本比较的Wilcoxon秩和检验来判断两样本均数的差异。检验水准取α=0.05。

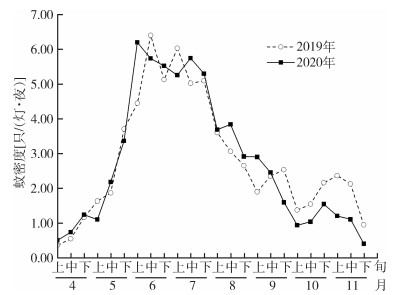
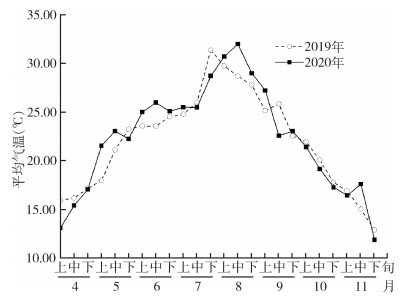
上海市2019和2020年4月上旬至11月下旬，15个区的229个CO₂诱蚊灯共捕获淡色库蚊雌蚊30 357只。上海市淡色库蚊于6月上旬开始至7月下旬出现密度高峰，7月下旬之后密度逐渐减小（图 1）。2019和2020年上海市平均气温从5月下旬起至9月中旬 > 23 ℃（图 2），与淡色库蚊雌蚊密度高峰期高度吻合。

图 1 上海市2019和2020年4－11月淡色库蚊密度的季节变化（CO2诱蚊灯法） Figure 1 Seasonal variation in Culex pipiens pallens density in Shanghai from April to November in 2019 and 2020 (by CO2 mosquito lamp)

图选项

图 2 上海市2019和2020年4－11月平均气温的变化情况 Figure 2 Changes in mean temperature in Shanghai from April to November in 2019 and 2020

图选项

公式（4）中，α取双侧0.05，β取单侧0.1，n为229，以2019年数据拟合泰勒幂方程，a为5.847，b为1.525^[4]，估算δ与淡色库蚊均数间方程，代入各项参数后模型为：δ=，见图 3、4中淡色库蚊密度与δ模型曲线。通过Wilcoxon秩和检验比较实验期间相邻，间隔1旬和2旬的淡色库蚊CO₂诱蚊灯监测的均数比较结果见表 1。2019年相邻2旬、间隔1旬和间隔2旬淡色库蚊监测密度比较，均值差异有统计学意义（均P < 0.05），占比分别为34.78%、59.09%和76.19%；2020年相邻2旬、间隔1旬和间隔2旬密度均值差异有统计学意义（均P < 0.05），占比分别为21.74%、59.09%和66.67%。实际CO₂诱蚊灯监测每旬密度值和拟合结果比较显示，2019年66个比较组中差异有统计学意义（均P < 0.05）的共37个，其中18个点在蚊密度与δ模型曲线上方，占48.64%（图 3）。2020年共66个比较组其中差异有统计学意义（均P < 0.05）的共32个，其中22个在蚊密度与δ模型曲线上方，占68.75%。见图 4。

注：统计学检验水准为α= 0.05；散点为2019年实际CO2诱蚊灯监测每旬密度和对应旬的密度差值。 图 3 上海市淡色库蚊密度与δ模型曲线及2019年监测结果比较 Figure 3 The relationship between Culex pipiens pallens density and δ model curve and comparison with the monitoring results in Shanghai in 2019

图选项

注：统计学检验水准为α= 0.05；散点为2020年实际CO2诱蚊灯监测每旬密度和对应旬的密度差值。 图 4 上海市淡色库蚊密度与δ模型曲线及2020年监测结果比较 Figure 4 The relationship between Culex pipiens pallens density and δ model curve and comparison with the monitoring results in Shanghai in 2020

图选项

表 1 淡色库蚊CO₂诱蚊灯法监测δ模型密度拟合结果与上海市2019和2020年监测结果差异统计学结果 Table 1 Statistical result of differences between the fitting density of Culex pipiens pallens from δ model by the mosquito lamp method and the monitoring density in Shanghai in 2019 and 2020

表选项

公式（5）中β₁和β₀通过2019年临近2旬的蚊密度δ与该2旬的前1旬间∆T拟合线性模型，拟合结果为：δ=(0.284±0.092)∆T-(0.069±0.154)。

图 5为2019年临近2旬的蚊密度差值（δ）与该2旬的前1旬间∆T实际监测值的散点图。

注：散点为临近2旬的蚊δ与其前1旬间平均气温差值。 图 5 2019年上海市淡色库蚊CO2诱蚊灯法监测基于温度差的蚊密度差拟合结果 Figure 5 Temperature difference-based linear fitting results of density difference of Culex pipiens pallens by CO2 mosquito lamp method in 2019

图选项

将线性回归结果代入公式（6），得：

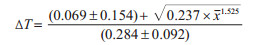
图 6、7为2019和2020年实际监测每旬密度分别和相邻2旬、间隔1旬和间隔2旬的温度差值的散点图；阴影部分为∆T > 0时95%置信区间（CI）下限与∆T < 0时95%CI上限间的区间，即本模型预测每次监测的淡色库蚊密度所对应的，在当前样本量下，α取双侧0.05、β取单侧0.1时，可监测到的密度差异无统计学意义模型预测的∆T区间。相邻、间隔1旬和2旬的淡色库蚊CO₂诱蚊灯监测的均数比较，与模型预测结果见表 2。2019年差异有统计学意义（均P < 0.05）的组与模型预测相符的占比为62.16%（阴影外），差异无统计学意义（均P > 0.05）的组与模型预测相符的占比为75.86%（阴影内）。2020年差异有统计学意义（均P < 0.05）的组与模型预测相符的占比为56.25%（阴影外），差异无统计学意义（均P > 0.05）的组与模型预测相符的占比为79.41%（阴影内）。

注：统计学检验水准为α= 0.05；散点为2019年实际监测每旬密度和相邻2旬、间隔1旬和间隔2旬的温度差值（∆T）；阴影部分为∆T > 0时95%置信区间下限与∆T < 0时95%置信区间上限间的区间。 图 6 淡色库蚊CO2诱蚊灯法监测基于温度差的抽样模型平均温度差值（∆T）预测值及与上海市2019年密度监测结果比较 Figure 6 ∆T from temperature difference-based sampling model of Culex pipiens pallens by the mosquito lamp method and comparison with monitoring results in Shanghai in 2019

图选项

注：统计学检验水准为α= 0.05；散点为2020年实际监测每旬密度和相邻2旬、间隔1旬和2旬的温度差值；阴影部分为∆T > 0时95%置信区间下限与∆T < 0时95%置信区间上限间的区间。 图 7 基于温度差的淡色库蚊CO2诱蚊灯法监测抽样模型∆T预测值及与上海市2020年监测结果比较 Figure 7 ∆T from temperature difference-based sampling model of Culex pipiens pallens by the mosquito lamp method and comparison with monitoring results in Shanghai in 2020

图选项

表 2 淡色库蚊CO₂诱蚊灯法监测基于温度差的抽样模型预测密度与上海市2019和2020年监测结果差异统计学结果 Table 2 Statistical result of differences between the predicted density of Culex pipiens pallens from temperature difference-based sampling model by the mosquito lamp method and the monitoring density in Shanghai in 2019 and 2020

表选项

通过计算准确率、召回率得F-measure，结果见表 3。2019和2020年CO₂诱蚊灯监测数据计算得到F-measure均 > 60.00%，模型有较好的拟合效果。

表 3 基于上海市2019和2020年CO₂诱蚊灯监测数据的温度差模型准确率、召回率和F-measure Table 3 Accuracy, recall, and F-measure of the temperature difference-based sampling model based on the CO₂ mosquito lamp monitoring data of Culex pipiens pallens in Shanghai in 2019 and 2020

表选项

病媒生物监测是病媒传播疾病风险评估、预警及科学防控的核心内容^[9]，需要连续、系统、科学地收集监测信息。本研究以2次监测间密度均数的差异是否有统计学意义为基础探寻高效的监测频次，从而避免监测频次过高导致资源的浪费和监测频次过低无法获得连续完整的密度变化信息。本研究首先通过之前建立的基于泰勒幂法则的模型，得到每次监测的密度均数与其方差间的函数关系，再代入两样本均数比较的样本量公式，得到某样本量下蚊密度均数与其差异有统计学意义的最小密度差δ的函数，建立基于密度差的CO₂诱蚊灯监测抽样模型。再以CO₂诱蚊灯监测结果拟合温度差与密度差线性模型，得到温度差与密度差的线性回归方程，代入基于密度差的CO₂诱蚊灯监测抽样模型，建立基于温度差的CO₂诱蚊灯监测抽样模型。

上海市目前的CO₂诱蚊灯监测频次为每旬1次，全市15个区共计229个监测点，每个监测点每次放置1个CO₂诱蚊灯。2019和2020年共开展监测46次，其中相邻2旬CO₂诱蚊灯监测密度均值差异有统计学意义的为28.26%（13/46），间隔1旬为59.09%（26/44），间隔2旬为71.43%（30/42）。相邻2旬的监测结果差异有统计学意义的占比较小，提示每旬1次的监测频次效率偏低，而间隔1旬有差异的比例约为60.00%，是一个比较合理的尺度。同时，依据基于温度差的抽样模型[公式（6）]，可计算给定u_α和u_β水平下，某样本量下能辨别的2次监测的最小密度均数的δ所对应的温度差。因此可以依此模型，以温度差为自变量预测其对应的密度差是否有统计学意义，适当在2旬间依据温度差预测的结果增加监测频次。同时，也可以某地的历史气象数据和样本量推算合理的监测频次。

其次，根据基于密度差的抽样模型[公式（4）]可知，样本量与能辨别的2次监测的最小密度均数δ成反比，样本量越小则需δ越大。由于CO₂诱蚊灯监测的成本较高^[10]，通常都不具有较大的样本量。对于样本量较小的监测区域，可能2次监测间差异有统计学意义要较大的δ值，即间隔时间大于1旬。因此，当样本量较小时我们推荐将监测按单次和双次分组，单次的监测点与双次的不同，将连续2次的监测结果作为1组样本量。则样本量是原来的2倍，可以分辨的差值δ则小于分组前。此方法可以在不增加成本的前提下，减少监测频次过高导致的2次监测间密度差异无统计学意义造成的资源浪费，还可以增加监测的效率（样本量是原来的2倍），以及获得更大范围的蚊密度值（监测点是原来的2倍）。

本研究基于上海市CO₂诱蚊灯监测数据建立了基于密度差和温度差的抽样模型，此模型可以计算合适的监测频次，同时也可以应用于其他的监测方法。今后的研究中可探寻拟合效果更佳的方法，如时间序列模型或神经网络模型^[11-13]。得到更好的预测监测频次的抽样模型，为监测的开展提供理论依据。

综上所述，基于温度差的抽样模型具备实用意义，可以根据温度差估算CO₂诱蚊灯监测的最佳监测频次。目前上海市的CO₂诱蚊灯监测于每年4－11月每旬监测1次，建议间隔1旬开展监测，并可根据温度变化适当增加频次。

利益冲突   无