扩展功能
文章信息
- 周毅彬, 朱奕奕, 朱伟, 姚隽一, 朱江, 冷培恩, 吴寰宇
- ZHOU Yi-bin, ZHU Yi-yi, ZHU Wei, YAO Jun-yi, ZHU Jiang, LENG Pei-en, WU Huan-yu
- 诱蚊诱卵器监测的空间抽样方法研究
- A study of spatial sampling methods for mosq-ovitrap monitoring
- 中国媒介生物学及控制杂志, 2021, 32(6): 749-755
- Chin J Vector Biol & Control, 2021, 32(6): 749-755
- 10.11853/j.issn.1003.8280.2021.06.019
-
文章历史
- 收稿日期: 2021-06-11
2 上海市徐汇区疾病预防控制中心, 上海 200237
2 Shanghai Xuhui District Center for Disease Control and Prevention, Shanghai 200237, China
病媒生物监测是预防和控制媒介生物传染病的重要环节,是公共卫生监测的重要组成部分。蚊媒监测为登革热等媒介生物传染病的监测预警及风险研判提供了重要依据,为预防和控制蚊媒传染病的传播发挥了重要的决策参考作用。针对蚊虫密度监测,选择有代表性的监测点是监测的首要任务,目前监测选点主要考虑既往蚊媒传染病的疫情情况和实际需求。具体实施时,一般以选择蚊虫孳生的最佳生境或疫情高发区最为常见[1]。目前上海市的蚊虫密度监测中使用范围最广,监测频次最高的方法为诱蚊诱卵器法。
然而,现阶段的监测方案中,无论采用哪一种监测方法,均未对监测点的抽样方法做更为详细的规范。此外,经典的抽样方法要求样本间相互独立,而蚊虫的分布具有空间相关的属性,例如,距离越接近的地点蚊密度越接近。因此,需要考察蚊媒监测选择的监测点是否具有足够的代表性。空间抽样有别于传统抽样,其抽样调查对象具有地理空间坐标,如果改变抽样对象的空间位置,则将影响抽样调查的结果[2]。因此在蚊虫监测调查工作中,应赋予蚊虫监测数据以空间位置的概念,监测结果同时包括地理空间坐标和属性值(如蚊虫密度值)。空间抽样方法与传统抽样调查方法相比,更具代表性,降低了抽样的不确定性,考虑了样本空间相关性和异质性,研究效率更高,精度更高[3],目前空间抽样模型已在社会发展的诸多领域中得到广泛应用[4-5],在公共卫生领域的应用也有一些有代表性的研究[6]。汪训平和赵安[7]基于植物分布丰度为辅助变量,优化了钉螺空间采样调查方法,并取得了更高的估算精确度。
本研究选择上海市中心城区的某一区域,以伊蚊监测的诱蚊诱卵器法监测数据为研究样本,基于蒙特卡罗模拟简单随机抽样和空间分层抽样,并计算空间抽样结果的绝对误差与抽样效率,评价不同抽样方法的精度和分层效率,探索空间属性对伊蚊监测结果的影响,从而为进一步设计结合空间抽样理论开展病媒生物监测的方法提供参考。
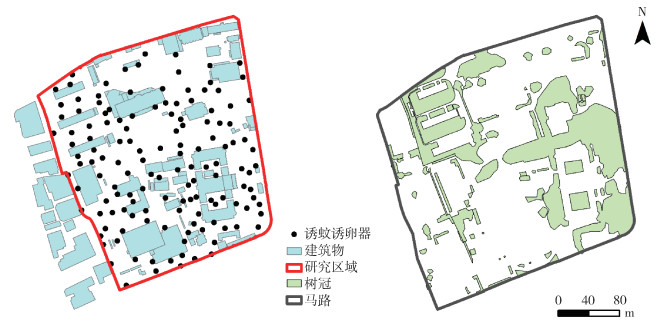
1 材料与方法 1.1 研究区域本次研究选取上海市中心一矩形区域,东西长约250 m、南北长约290 m。由研究区域西北角的居民小区和1个科教园区组成。研究区域内共有14幢大小不一的建筑,其中三侧紧邻马路,西侧与马路间有一片居民区(图 1)。该区域是较为典型的上海市市中心类型,有较好的植被和较高人流量,且之前的研究显示蚊密度在该区域分布具有高密度和低密度聚集区的空间特征[8]。
|
| 图 1 诱蚊诱卵器空间抽样方法研究区域景观和诱蚊诱卵器布放示意图 Figure 1 Landscapes and mosq-ovitrap layout diagrams of study area for spatial sampling method of mosq-ovitrap monitoring |
| |
本次研究使用诱蚊诱卵器法监测白纹伊蚊密度。每次将诱蚊诱卵器放在相同的位置,选取光线较强的绿化地带,相隔20 m设置监测点,每点布放1只诱蚊诱卵器。共放置150只诱蚊诱卵器,对每个监测点进行定位和编号。研究时间为2020年8月4日至9月1日(上海市白纹伊蚊密度较高时段),每次监测时间持续7 d,于第8天回收并观察,共监测4次。诱蚊诱卵器内有白纹伊蚊成蚊或(和)蚊卵的,判定为阳性;既无成蚊也无蚊卵的,判定为阴性;诱蚊诱卵器丢失、干涸或破损等,判定为无效。在试验期间共计12个监测点的诱蚊诱卵器被判定为无效,将其余有效的138个诱蚊诱卵器的数据纳入分析。见图 1。

|
使用ArcGIS 10.8软件进行空间分析。全局空间自相关分析采用全局Moran’s I指数[9];全局Moran’s I可以识别整个研究区域的空间格局,但是无法确定某一位置的空间格局。局部Moran’s I指数(Local Moran’s I)分析用以评估每一监测位置是否存在具有统计学意义的聚集、冷点和空间异常值的点[10]。
1.4 抽样方法以138个诱蚊诱卵器的监测结果作为总体,采用蒙特卡罗(Monte Carlo)模拟的方法进行抽样。
蒙特卡罗模拟使用Python 3.8软件实现,每种抽样方法分别抽取15、20、25……80个诱蚊诱卵器,每个样本量模拟次数为1 000次。
1.4.1 简单随机抽样在总体中任意抽取n个诱蚊诱卵器作为样本,每个样本被抽中的概率相等。
1.4.2 九宫格空间分层抽样使用ArcGIS 10.8软件在研究区域外生成最小外接矩形,再使用ArcGIS 10.8软件的“渔网”工具生成x轴和y轴同为外接矩形边长三等分的9个渔网(图 2),以得到9片尽可能面积相等且在空间上均匀分布的空间分层区域,进行九宫格空间分层抽样(方法1)。如有监测点落在相邻2个区域的交界上,则该点同时归入相邻2个区域(下同,本次研究期间未发生)。

|
| 图 2 诱蚊诱卵器监测九宫格分层抽样 Figure 2 3×3 grid stratified sampling for mosq-ovitrap monitoring |
| |
使用ArcGis 10.8软件的“渔网”工具在研究区域生成x轴和y轴同为10 m边长的网格(图 3)。再以每个网格生成半径为45 m的缓冲区,与图 1中四边马路范围内的树冠面积做相交后计算每个缓冲区内的树冠面积,作为这个网格的属性值。使用GeoDa 1.14.0软件的非监督学习的SKATER空间聚类工具[11],对研究区域内的渔网空间聚类分层,分为6片区域,生成基于树冠面积的空间分层抽样(方法2)。

|
| 注:不同颜色代表不同分层区域。 图 3 诱蚊诱卵器监测基于树冠面积的空间分层抽样 Figure 3 Spatially stratified sampling based on tree crown area for mosq-ovitrap monitoring |
| |
以每个诱蚊诱卵器4次监测结果为4个属性值(阳性为1,阴性为0),使用GeoDa 1.14.0软件的SKATER空间聚类工具,对研究区域内的诱蚊诱卵器空间聚类分层(图 4),生成基于诱蚊诱卵器监测结果的空间分层抽样(方法3)。

|
| 注:不同颜色代表不同分层区域;1、2、3、4、5表示不同聚类的组。 图 4 诱蚊诱卵器监测基于不同监测结果的空间分层抽样 Figure 4 Spatially stratified sampling based on monitoring results for mosq-ovitrap monitoring |
| |
上述3种空间抽样方法中,每个区域内采用等比例抽样方法分配样本量,每一层内采用简单随机抽样。
1.5 统计学分析采用Excel 2007软件进行数据录入和整理,SPSS 20.0软件进行统计分析。对抽样的结果计算绝对误差与抽样效率,评价不同抽样方法的精度和分层效率。

|
抽样效率值越大,表示分层效率越高,反之,分层效率越低。检验水准取α=0.05。
2 结果 2.1 诱蚊诱卵器监测情况2020年8月4日至9月1日诱蚊诱卵器监测结果见表 1。研究区域内室外积水较少,白纹伊蚊孳生地以雨水井为主,研究期间研究区域未开展蚊虫密度控制。本次研究期间,4次监测的平均MOI为49.46。以每个诱蚊诱卵器4次监测的总阳性次数为其属性值,不同半径距离的全局空间自相关分析结果显示,空间自相关峰值半径为45 m,Moran’s I指数为0.289,Z值为7.874(P < 0.001),即空间自相关在半径45 m达到最大值(表 2)。局部空间自相关分析显示,在研究区域西北角呈现高密度与高密度聚集区,西南角为低密度与低密度聚集区,东侧大部分为无聚集区。见图 5。

|
| 图 5 诱蚊诱卵器监测结果局部空间自相关分析结果 Figure 5 Local spatial autocorrelation analysis of monitoring results by mosq-ovitrap |
| |
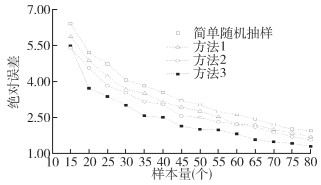
不同空间抽样方法采用1 000次蒙特卡罗模拟得到的平均绝对误差比较结果见图 6。横坐标为抽样数量,模拟的抽样范围为15、20、25……80个诱蚊诱卵器。4次监测结果中,4种抽样方法绝对误差均随着抽样量的增加而逐步减小,其中空间分层抽样方法3绝对误差最小,其次为空间分层抽样方法2。2020年8月18日第3次监测,几种不同抽样方法绝对误差的差异最大。以4次监测的平均值为统计量,4种抽样方法绝对误差比较见图 7,空间分层抽样方法3绝对误差最小,当样本量 > 35个诱卵器时,其绝对误差 < 2.50。

|
| 方法1指九宫格空间分层抽样;方法2指基于树冠面积的空间分层抽样;方法3指基于诱蚊诱卵器监测结果的空间分层抽样。 图 6 诱蚊诱卵器法不同监测时间不同抽样方法绝对误差比较 Figure 6 Absolute error comparison among different sampling methods at different monitoring times of mosq-ovitrap monitoring |
| |
|
| 注:方法1指九宫格空间分层抽样;方法2指基于树冠面积的空间分层抽样;方法3指基于诱蚊诱卵器监测结果的空间分层抽样。 图 7 诱蚊诱卵器法不同抽样方法4次监测平均绝对误差比较 Figure 7 Comparison of mean absolute error of four monitoring activities in different sampling methods for mosq-ovitrap monitoring |
| |
不同空间抽样方法采用1 000次蒙特卡罗模拟得到的平均抽样效率的比较见图 8。4次监测结果中,3种空间分层抽样方法的抽样效率大多在1.00以上,其中空间分层抽样方法3抽样效率最高,其次为空间分层抽样方法2。以4次监测的平均值为统计量,3种空间分层抽样方法抽样效率比较见图 9,方法3绝对误差最小,方法2略高于方法1。

|
| 注:方法1指九宫格空间分层抽样;方法2指基于树冠面积的空间分层抽样;方法3指基于诱蚊诱卵器监测结果的空间分层抽样。 图 8 诱蚊诱卵器法不同监测时间不同空间抽样方法抽样效率比较 Figure 8 Sampling efficiency comparison between different spatial sampling methods at different monitoring time of mosq-ovitrap monitoring |
| |

|
| 注:方法1指九宫格空间分层抽样;方法2指基于树冠面积的空间分层抽样;方法3指基于诱蚊诱卵器监测结果的空间分层抽样。 图 9 诱蚊诱卵器法不同空间抽样方法四次监测平均抽样效率比较 Figure 9 Comparison of mean sampling efficiency of four monitoring activities in different spatial sampling methods for mosq-ovitrap monitoring |
| |
蚊虫监测的数据是掌握区域蚊虫密度及分布,评估灭蚊措施等工作的重要依据。如何通过抽样调查的方法,获得病媒监测对象的数量特征,推断总体蚊虫分布,并评估控制效果,是病媒生物监测工作的难点。作为地理空间对象,蚊虫分布通常存在一定的空间自相关性,距离接近的样本点会有一定程度的相关性(协方差不等于0),很难吻合经典抽样方法独立性假设的前提条件。空间分层抽样是在经典抽样的基础上,将研究区域按其空间属性特征进行分层,分层均是基于空间连续的分层,即某一层内所有样本点一定位于1个连通区域内。空间分层抽样方法的核心是得到具有最高抽样效率的分层方式,分层的目的是使分层效率尽量大。
本次研究区域的白纹伊蚊密度分布具有空间自相关性和异质性。全局Moran’s I指数在半径45 m达到最大值,局部空间自相关分析提示在研究区域分布有高密度与高密度聚集区,低密度与低密度聚集区。抽样总体的地理空间相关性特征影响地理空间对象的分层抽样的效率[12]。本文采用了4种抽样方式:
方式1:简单随机抽样,诱蚊诱卵器在空间上随机布设,可能使一些诱蚊诱卵器在空间上聚集,而在另外一些区域出现空白,聚集和空白地带的诱蚊诱卵器的不均衡使样本对抽样总体的代表性降低;
方式2:九宫格空间分层抽样(方法1),将研究区域分为9片尽可能面积相等的空间分层区域,此方法追求诱蚊诱卵器布设的空间均匀性。通常在常规监测中,大多数时候也是这样安排样本点。此方法与简单随机抽样方法相比,抽样的绝对误差和抽样效率均有提高;
方式3:基于树冠面积的空间分层抽样(方法2),将与白纹伊蚊孳生密切相关的辅助变量树冠分布作为分层依据[13],以蚊虫密度空间自相关峰值45 m为半径[8],辅助分层抽样。以树冠分布作为辅助变量,不需要进行目标蚊虫分布的预实验,抽样的绝对误差和抽样效率均优于九宫格空间分层;
方式4:基于诱蚊诱卵器监测结果的空间分层抽样(方法3),以蚊虫密度分布为依据将其作为先验数据作为分层依据,是4种抽样方法中效果最好的。由于白纹伊蚊的密度空间分布具有稳定性[14],因此实际监测工作中可以根据预实验结果调整诱蚊诱卵器的样本点分布,在相同样本量的前提下获取更接近总体的监测数据。
当样本量相同时,3种空间分层方法相比简单随机抽样均取得了更高的估计精度,这是由于它们能使样本点的空间分布更分散,使样本点信息重叠的可能性得到降低[15]。同时以抽样密度为绝对误差 < 2.50为例,方法3至少需要35个诱蚊诱卵器,方法2至少需要45个诱蚊诱卵器,方法1至少需要55个诱蚊诱卵器,而简单随机抽样至少需要65个诱蚊诱卵器(图 7)。更好的分层方法也能显著减少监测所需的诱蚊诱卵器的样本量。文中采用3种空间分层抽样方法,其中方法1为空间均匀的抽样方法,实际可操作性最强。方法2基于树冠分布,结果比方法1抽样更靠近整体均值。方法3精度最高,但需基于现有监测结果进行区域划分后再进行抽样,实际工作中设计和实施难度均较大。利用蚊虫密度分布的相关模型[16]结合方法3是我们下一步的研究方向,在提高抽样精度的前提下改善方法3的可操作性。
本文也存在不足,未考虑诱蚊诱卵器数量不同时,诱蚊诱卵器监测结果的变化。本次主要研究了在重采样条件下,不同布点数量和位置的变化。实际监测中,空间单位通常为1个街镇,诱蚊诱卵器数量对整个区域的积水数影响较小,对于较小范围的空间抽样方法研究还需进一步的完善。
综上,空间分层抽样可以提高诱蚊诱卵器监测效率,不同的分层方法具有不同的效率值。更好的先验知识指导高效空间分层是空间抽样框架下分层抽样方法的不二选择,当分层是基于有效的先验知识时,空间分层抽样能够获得比简单随机抽样方法高得多的精度。结合辅助变量和蚊密度空间分布模型,用于空间抽样的先验知识也将是我们下一步的研究方向。
利益冲突 无
| [1] |
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. GB/T 23797-2020病媒生物密度监测方法蚊虫[S]. 北京: 中国标准出版社, 2020. General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, Standardization Administration of China. GB/T 23797-2020 Surveillance methods for vector density-Mosquito[S]. Beijing: China Standard Press, 2020. |
| [2] |
姜成晟, 王劲峰, 曹志冬. 地理空间抽样理论研究综述[J]. 地理学报, 2009, 64(3): 368-380. Jiang CS, Wang JF, Cao ZD. A review of geo-spatial sampling theory[J]. Acta Geograph Sin, 2009, 64(3): 368-380. DOI:10.3321/j.issn:0375-5444.2009.03.012 |
| [3] |
张杰, 赵春香, 张健, 等. 空间抽样技术研究进展及其在公共卫生领域的应用[J]. 中华劳动卫生职业病杂志, 2016, 34(3): 236-239. Zhang J, Zhao CX, Zhang J, et al. Research progress of spatial sampling technology and its application in public health[J]. Chin J Ind Hyg Occup Dis, 2016, 34(3): 236-239. DOI:10.3760/cma.j.issn.1001-9391.2016.03.022 |
| [4] |
陈飞香, 戴慧, 胡月明, 等. 区域土壤空间抽样方法研究[J]. 地理与地理信息科学, 2012, 28(6): 53-56. Chen FX, Dai H, Hu YM, et al. Study on regional soil spatial sampling method[J]. Geogr Geo-Inf Sci, 2012, 28(6): 53-56. |
| [5] |
张小伟, 佘光辉, 温小荣, 等. 空间分层抽样在森林覆盖面积监测中的应用[J]. 南京林业大学学报(自然科学版), 2012, 36(3): 81-84. Zhang XW, She GH, Wen XR, et al. The application of spatial stratified sampling in remote sensing monitoring of forest cover[J]. J Nanjing For Univ (Nat Sci Ed), 2012, 36(3): 81-84. DOI:10.3969/j.issn.1000-2006.2012.03.017 |
| [6] |
杨国静, 周晓农, 汪天平, 等. 安徽、江西及江苏3省血吸虫病患者与钉螺分布的空间自相关分析[J]. 中国寄生虫学与寄生虫病杂志, 2002, 20(1): 6-9. Yang GJ, Zhou XN, Wang TP, et al. Spatial autocorrelation analysis on schistosomiasis cases and Oncomelania snails in three provinces of the lower reach of Yangtze River[J]. Chin J Parasitol Parasit Dis, 2002, 20(1): 6-9. DOI:10.3969/j.issn.1000-7423.2002.01.002 |
| [7] |
汪训平, 赵安. 以植物丰度为辅助变量的钉螺空间分层采样研究[J]. 中国血吸虫病防治杂志, 2017, 29(4): 420-425. Wang XP, Zhao A. Study of spatial stratified sampling strategy of Oncomelania hupensis snail survey based on plant abundance[J]. Chin J Schisto Control, 2017, 29(4): 420-425. DOI:10.16250/j.32.1374.2017036 |
| [8] |
朱伟, 戈斌, 李澜, 等. 空间分析在诱蚊诱卵器监测中的应用研究[J]. 寄生虫与医学昆虫学报, 2020, 27(3): 158-163. Zhu W, Ge B, Li L, et al. The study of the monitoring by mosq-ovitraps with spatial analysis[J]. Acta Parasitol Med Entomol Sin, 2020, 27(3): 158-163. DOI:10.3969/j.issn.1005-0507.2020.03.004 |
| [9] |
Moran PAP. Notes on continuous stochastic phenomena[J]. Biometrika, 1950, 37(1/2): 17-23. DOI:10.1093/biomet/37.1-2.17 |
| [10] |
Anselin L. Local indicators of spatial association-LISA[J]. Geograph Anal, 1995, 27(2): 93-115. DOI:10.1111/j.1538-4632.1995.tb00338.x |
| [11] |
胡健, 胡艺, 高风华, 等. 基于SKATER聚类算法设计血吸虫病监测点的探索性研究[J]. 中国血吸虫病防治杂志, 2019, 31(4): 368-373. Hu J, Hu Y, Gao FH, et al. Design of schistosomiasis surveillance sites based on spatial kluster analysis by tree edge removal (SKATER) method: an exploratory study[J]. Chin J Schisto Control, 2019, 31(4): 368-373. DOI:10.16250/j.32.1374.2019011 |
| [12] |
曹志冬, 王劲峰, 李连发, 等. 地理空间中不同分层抽样方式的分层效率与优化策略[J]. 地理科学进展, 2008, 27(3): 152-160. Cao ZD, Wang JF, Li LF, et al. Strata efficiency and optimization strategy of stratified sampling on spatial population[J]. Prog Geogr, 2008, 27(3): 152-160. DOI:10.11820/dlkxjz.2008.03.021 |
| [13] |
Cianci D, Hartemink N, Zeimes CB, et al. High resolution spatial analysis of habitat preference of Aedes albopictus (Diptera: Culicidae) in an urban environment[J]. J Med Entomol, 2015, 52(3): 329-335. DOI:10.1093/jme/tjv026 |
| [14] |
周毅彬, 朱奕奕, 朱江, 等. 上海市白纹伊蚊空间稳定性研究[J]. 中国媒介生物学及控制杂志, 2021, 32(2): 127-131. Zhou YB, Zhu YY, Zhu J, et al. A study of spatial stability of Aedes albopictus in Shanghai, China[J]. Chin J Vector Biol Control, 2021, 32(2): 127-131. DOI:10.11853/j.issn.1003.8280.2021.02.002 |
| [15] |
Dunn R, Harrison AR. Two-dimensional systematic sampling of land use[J]. J Roy Stat Soc, 1993, 42(4): 585-601. DOI:10.2307/2986177 |
| [16] |
Zheng JX, Xia S, Lyu S, et al. Infestation risk of the intermediate snail host of Schistosoma japonicum in the Yangtze River basin: improved results by spatial reassessment and a random forest approach[J]. Infect Dis Poverty, 2021, 10(1): 74. DOI:10.1186/s40249-021-00852-1 |
 2021, Vol. 32
2021, Vol. 32




