2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
遥感影像配准是遥感图像处理的重要研究内容,是决定图像融合、目标变化检测和识别、拼接和镶嵌等过程精度和应用效果的关键因素。目前卫星影像的空间分辨率不断提高,例如国内在2013年已经逐步开始使用的高分2号卫星系列,可以生产0.81 m全色卫星影像,3.24 m多光谱卫星影像[1];对高分辨率遥感影像来说,像元包含的地物细节信息更加丰富,因此易受时相、拍摄角度、光照等影响,出现错匹配,局部区域过拟合、欠拟合导致配准效果不佳等问题。
近年来,国内外学者在影像自动匹配方面做了大量研究。例如基于灰度信息的匹配方法,直接利用2幅图像之间灰度度量的相似性,逐像元计算影像变换参数。这种方法虽然实现简单,但其缺点是运算量较大,不适合数据量丰富的高分辨率遥感影像。另一种是基于特征的匹配方法,这种方法中,点特征最为常用:通过计算2幅图像上信息丰富的特征点,实现控制点之间的匹配对应,从而计算出变换模型,完成图像几何校正。代表有Lowe[2]提出的尺度不变特征变换(scale invariant feature transformation, SIFT)算法。SIFT算法提取点特征,可以在保证图像信息量的同时,降低计算的数据量,不易受光照、尺度、旋转等因素影响,相比于其他点特征提取方法,对视角变换有一定的稳定性,故成为遥感影像配准领域的主流特征提取方法。但在应用SIFT算法对高分辨率遥感影像进行图像配准时,仍然存在计算复杂、匹配错误、特征点分布不均、局部配准结果过拟合或欠拟合等问题。
为解决算法在遥感影像匹配过程中产生的错提取、错匹配问题,Yan等[3]提出基于迁移学习的优化方法进行多模态的遥感影像配准。Jiang等[4]提出基于线性自适应滤波的方法用于遥感图像的刚性和非刚性匹配,提升了影像配准的精度。Zhang等[5]通过利用Harr小波响应为每个特征点建立描述符,计算领域内归一化灰度差和二阶梯度,形成新的描述符,提高了特征点匹配的速度并获得了更高的光照鲁棒性。Sedaghat和Mohammadi[6]提出一种基于扩展自相似性度量的新型描述符,通过计算各个方向自相似值的构建,生成最大相关旋转系数索引图,可以有效提升遥感图像匹配对于光照的鲁棒性。Ma等[7]提出一种基于可变阈值和变分混合变换的遥感图像配准方法,使用一种引导高斯混合模型更好地区分离群点、提升配准精度的方法。Yang等[8]提出一种基于相位相关性的方法进行离群点的剔除,通过粗配准和精配准结合的方法提高精度。Zhang等[9]改进了SIFT方法的尺度空间构建,通过计算梯度幅度用圆形描述符代替方型描述符,达到了亚像素级精度。
针对算法计算复杂、局部过拟合或欠拟合的问题,Liu等[10]提出一种有限状态混沌压缩遥感云的图像配准方法,在云平台上提高了图像处理速度,并通过改进局部和全局信息减少纹理相似性带来的影响,提高了配准精度。Zhang等[11]将基于深度图像类比的传递算法应用到图像配准中,基于图像深层语义特征的联系,间接实现了原始图像对的匹配,为多模态图像配准问题提供了新的方法。Zhou等[12]提出基于子图像的配准方法,将参考图像划分为大小相等的子图像,并利用小波变换技术提取小波系数综合最大的子图像作为新的参考图像,然后利用相位相关和矩阵乘法离散傅里叶变换算法的两步方法将感测图像配准到参考子图像,在实现亚像素级配准精度的前提下节省了配准时间。
以上配准方法针对性地提高了配准的精度和效率,但对因为地形起伏、地物类型丰富导致不同区域的空间错位不一致[13],存在复杂变换模型的问题缺乏考虑,这使得基于全局的变换模型容易出现局部区域拟合失真的问题。要实现局部区域高精度配准,需要构建配准局部模型[14]。对于局部模型的构建,一般使用基于Zaeagoza等[15]提出的尽可能投影(as-projective-as-possible,APAP)方法衍生的地理分区策略,将影像分为C1×C2组单元,求解每组单元的投影矩阵。然而APAP方法受区块划分单元的数量影响较大,划分数量多则计算复杂,容易累计投影失真;反之则区分效果不佳。导致以上问题的原因在于此种方法不能模拟遥感影像中包含子区域的真实情况。本文提出一种基于层次聚类思想的模型一致分区快速配准方法,可以解决配准过程中的子区域多模型估计问题[16]。该方法首先结合SIFT匹配点分布规律进行采样,获得初始类别,并计算变换模型,然后根据匹配点对不同变换模型的符合程度构建倾向集,最后将倾向集合并,有效得到聚类结果,根据聚类结果生成泰森多边形进一步完整划分子区域,计算各个区域的变换模型并插值拼接,完成整幅影像的配准。
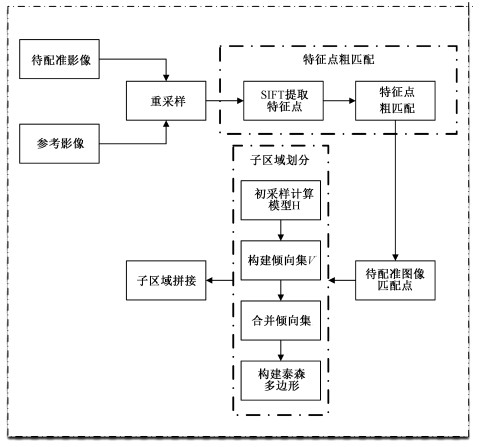
1 方法本文方法基本流程如下:
1) 在重采样影像上利用差分尺度约束提取更高精度的SIFT的特征点并生成基于Hellinger变换的描述子,根据k-D树(k-dimensional tree)加速的KNN进行特征匹配。
2) 使用层次聚类方法分析匹配点对不同变换模型的符合倾向,完成影像子区域数目和位置的划分,获得匹配点的聚类结果。根据聚类中心生成泰森多边形,划分影像子区域。
3) 在子区域内分别根据精匹配点计算变换模型,完成插值融合。
根据上述算法步骤,总结算法具体流程如图 1所示。
|
Download:
|
| 图 1 改进方法流程图 Fig. 1 Flow chart of improved method | |
SIFT方法包括建立高斯差分尺度空间,提取关键点、生成描述子、特征点匹配3个主要过程,应用在高分辨率影像上时存在错匹配、耗时长的问题。本文结合差分尺度空间约束在高分辨率影像上提取更高精度的特征点,并结合Hellinger变换改进描述子,减少算法耗时。
1) 提取差分尺度空间约束的特征点:构建高斯金字塔,自底层向上层排列分为n阶,每阶归为一组,对每组图像采用不同尺度的高斯核卷积,生成模糊程度不同的K层图像。
| $ \boldsymbol{L}(\boldsymbol{x}, \boldsymbol{y}, \sigma)=\boldsymbol{G}(\boldsymbol{x}, \boldsymbol{y}, \sigma) * \boldsymbol{I}(\boldsymbol{x}, \boldsymbol{y}) $ | (1) |
| $ \begin{gathered} \boldsymbol{D}(\boldsymbol{x}, \boldsymbol{y}, \sigma)=(\boldsymbol{G}(\boldsymbol{x}, \boldsymbol{y}, k \sigma)-\boldsymbol{G}(\boldsymbol{x}, \boldsymbol{y}, \sigma)) * \\ \boldsymbol{I}(\boldsymbol{x}, \boldsymbol{y}) \end{gathered} $ | (2) |
式(1)为高斯核函数G与该层原始图像I卷积生成模糊图像L。式(2)为使用高斯差分函数(difference of Gaussian, DoG)对影像卷积,构建高斯差分尺度空间。其中x, y为向量,σ为高斯核尺度因子。
在高斯差分序列中提取极值点:当点的灰度值为3层8-邻域空间26个像素点的极值时,选取该点作为极值点。算法得到的特征点属于不同尺度层,特征点的误差与其所在尺度呈正比关系[17],由尺度因子概念可得,当尺度因子σ < 1时,点精度优于高分2号多光谱影像1个像元(4 m),实验中选择1.5作为尺度因子的取值,将高于这一阈值的点从初始集合中删去,基于差分尺度约束,得到精度更高的特征点。
2) 生成基于Hellinger变换的描述子:一般的SIFT方法通过以特征点为中心,取16×16窗口,以4×4划分子方块,根据幅值和方向计算每个子块的梯度直方图。传统的SIFT方法使用欧式距离来比较直方图,获得128维的特征向量s。当进行直方图比较时,采用欧式距离的性能比Hellinger核性能差[18]。因此本文使用Hellinger变换优化描述子,提升量化精度和匹配性能。
对于单位向量
| $ d_{\mathrm{E}}(\hat{\boldsymbol{x}}, \hat{\boldsymbol{y}})=\|\hat{\boldsymbol{x}}-\hat{\boldsymbol{y}}\|_2^2=2-2 S_{\mathrm{E}}(\hat{\boldsymbol{x}}, \hat{\boldsymbol{y}}) . $ | (3) |
| $ S_{\mathrm{E}}(\hat{\boldsymbol{x}}, \hat{\boldsymbol{y}})=\hat{\boldsymbol{x}}^{\mathrm{T}} \hat{\boldsymbol{y}} . $ | (4) |
对于l1的归一化后的单位向量
| $ H(\hat{\boldsymbol{x}}, \hat{\boldsymbol{y}})=\sum\limits_i^n \hat{\boldsymbol{x}}_i \hat{\boldsymbol{y}}_i . $ | (5) |
使用Hellinger变换优化特征向量的方法为:
① 对SIFT特征向量s进行l1的归一化得到s′。
② 对s′的每一个元素求平方根得到h。
通过步骤①、步骤②得到新的描述符h,它是l1归一化后SIFT向量的元素平方根。
由式(3)~式(5)可推导得
| $ S_{\mathrm{E}}(\sqrt{\hat{\boldsymbol{x}}}, \sqrt{\hat{\boldsymbol{y}}})=\sqrt{\hat{\boldsymbol{x}}}^{\mathrm{T}} \sqrt{\hat{\boldsymbol{y}}}=H(\hat{\boldsymbol{x}}, \hat{\boldsymbol{y}}) . $ | (6) |
| $ d_{\mathrm{E}}(\sqrt{\hat{\boldsymbol{x}}}, \sqrt{\hat{\boldsymbol{y}}})^2=2-2 H(\hat{\boldsymbol{x}}, \hat{\boldsymbol{y}}) . $ | (7) |
式(7)表示使用欧氏距离比较描述符h,与使用Hellinger核对原始向量进行比较是等价的,实践中在每个点用 h替代原始向量使用欧式距离比较,即可提高直方图比较的性能。在后文实验中对效果进行比对。
3) 特征点匹配:对2)中生成的描述子做欧氏距离量测,记录最邻近的点D1和次临近的点D2,将这2个距离的比值与阈值d比较,比值小于等于d的特征点接受为匹配点,否则删去。
| $ \frac{D_1}{D_2} \leqslant d \text {. } $ | (8) |
本文采用k-D树建立待匹配特征向量集的索引,通过k-D树查找D1和D2,可以大大缩小搜索范围,提升效率。方法根据数据的方差,在k维空间上划分层次,提高查找效率。
1.2 特征信息聚类分区大量实验表明,由于地形起伏大、地物种类丰富等原因,高分辨率影像配准的全局变换模型应用于局部区域会带来大量误差。本文基于层次聚类方法,对待配准影像的特征信息进行分区处理,分别实现局部精细配准。算法通过计算每个点对于局部模型的符合情况,筛选出属于同一局部区域且符合区域变换模型的匹配点,得到合理的分区效果和匹配点筛选结果。具体方法如下:
1) 随机采样生成初始模型:采用最邻近优先采样准则,随机选择N个匹配点对,变换模型采用二次多项式模型,模型需要的最小匹配点对为6个,故N=6。记这N个点对的集合为M。M中的第1个元素N1采用随机采样,即P(N1)=1/m, P为采样概率,m为总匹配点对个数,e为自然对数的底,σ为可求解参数。剩余采样点的采样概率遵循下式
| $ P\left(N_i \mid N_1\right)=\left\{\begin{array}{l} \frac{1}{Z} \mathrm{e}^{\left(\frac{-\left\|N_i-N_1\right\|}{\sigma^2}\right)}, \quad i=2, 3 \cdots . \\ 0, \end{array}\right. $ | (9) |
其中,
获得初始采样集合M后,计算M对应的变换模型H。
2) 重复采样并生成倾向集:重复1)中采样计算过程K次,得到Hs(s=1, 2…K)。计算每组匹配点对Pi(x, y)i1(x, y)i2与 Hs的模型误差ei, s,其中i为匹配点对的序号,x, y为点的坐标值。如下式所示
| $ \boldsymbol{e}_{i, s}=\boldsymbol{H}_s(x, y)_i^1-(x, y)_i^2 . $ | (10) |
设定一致性阈值ε,当ei, s≤ε时,认为该组匹配对符合Hs。根据下边生成每一组点对P的倾向集V。
| $ V_i=\left[v_{i, 1}, v_{i, 2}, \cdots v_{i, K}\right] . $ | (11) |
| $ v_{i, n}=\left\{\begin{array}{ll} 1, & e_{i, n}<\varepsilon, \\ 0, & \text { else } \end{array}\ \ \ n \in[1, K] .\right. $ | (12) |
匹配对Pi(i=1, 2, …, m)的对应倾向集为Vi(i=1, 2, …, m)。
3) 合并集合:
| $ D\left(V_a, V_b\right)=\frac{\left|V_a \cup V_b\right|-\left|V_a \cap V_b\right|}{\left|V_a \cup V_b\right|} . $ | (13) |
| $ V_{a, b}=V_a \cap V_b . $ | (14) |
根据式(13)计算所有倾向集Vi(i=1, 2, …, m)的距离D,将距离最近的匹配对合并为新类,根据式(14)对类的倾向集作交集,将求交后的集合Va, b作为新类的倾向集。
其中D代表集合的Jaccard距离,Vi代表匹配点对i的倾向集。
4) 重复步骤3),至min D=1时,终止循环。
5) 将聚类后各类别的几何中心作为离散点构建泰森多边形,完成影像子区域划分。
参数K的大小影响了算法的精度和执行效率。对于确定数量的m组匹配点对,当K值不断增大时,算法精度提升;根据计算过程可知,该方法的时间复杂度为O(m3K),故提升K值会导致聚类的时间效率下降;当K足够大时,由于初始类别出现过多聚集,继续提升K值将不会带来计算精度的提升。需根据影像场景的复杂程度确定K值的大小。参数ε的大小影响了对匹配点集合中不属于任意区域变换模型的离群点的搜索能力。经过层次聚类划分,每个类别的匹配点可以更好地拟合所在区域的变换模型,且不属于任意变换模型的匹配点会作为错点被剔除,从而提高匹配点的正确率。
1.3 子区域插值拼接通过对聚类结果构建泰森多边形的方法完成全部像素的子区域划分后,在子区域利用子区域匹配点分别计算二次多项式变换模型,采用最邻近插值方法完成重采样,将各个子区域配准后的部分完成插值拼接。为避免在子区域插值拼接时出现空区域,可以根据实际情况设置子区域重叠宽度为S。对于插值后可能出现重复填充的位置,只保留第1次插值结果。
2 实验和分析 2.1 数据和软硬件环境本文的实验数据由表 1中描述的3组高分2号、1组高分1号卫星拍摄的遥感影像组成,为测试算法的配准效果,选取4种有代表性的影像地物类型完成配准实验。实验参考图像选取待配准影像对应位置经过坐标精校正的world-view2遥感卫星影像,初始分辨率为1.8 m,重采样至与待配准影像同一分辨率。为取得更好的配准和叠加效果,参考影像统一相较于待配准影像扩大300~500像素的包含范围。参考图像和待配准影像如图 2所示。图中每对影像左侧为待配准影像。
|
|
表 1 实验数据 Table 1 Experimental data |

|
Download:
|
| 图 2 实验影像 Fig. 2 Experimental images | |
实验分析分为3部分:
实验1展示了使用不同变换模型的局部地区配准后叠加结果。
实验2展示了使用本文改进的SIFT特征点粗匹配方法和改进前提取效果的对比。
实验3则分别使用本文方法与其他当前常用的改进算法对选定的影像对进行配准处理,从目视配准效果、像素偏移量、坏点个数和匹配正确率4个角度对处理结果进行比较和分析,验证本文方法的有效性和可行性。
实验中代码使用C++编程语言编写。
所用计算机配置为Intel(R)Core i5-9500 CPU@3.00 GHz,内存16 GB。
2.2 局部模型与全局模型的对比在整幅影像上手动选取控制点计算得到全局二次多项式模型,重采样后截取局部区域得到图 3(b)。采用图 3(b)区域的控制点计算局部二次多项式模型,对该区域重采样并将配准后影像叠加在参考影像上得到图 3(a),其中图 3(b)的配准结果出现比较大的偏差,而使用其对应区域的匹配点单独计算时可以取得如图 3(a)所示较好的拟合结果。计算其均方根误差(root mean squared error, RMSE)分别为0.112 3和3.541 7。综合目视匹配效果和均方根误差计算结果实验证明在进行高分辨率遥感影像配准时,基于整幅影像的配准模型会在局部区域产生配准失真,无法正确拟合。

|
Download:
|
| 图 3 采用不同模型的局部配准效果 Fig. 3 Local registration results using different models | |
本文中基于差分尺度空间约束方法和Hellinger变换改进了SIFT方法选取特征点和生成描述子的过程,图 4(a)是改进前的待配准影像上的粗匹配点,经改进后图 4(b)上的粗匹配点部分区域分布过密的现象得到了消除,在分布上更加均匀。

|
Download:
|
| 图 4 采用不同方法的粗匹配点 Fig. 4 Coarse matching points using different methods | |
对影像1~影像4采用传统SIFT方法和本文的改进方法分别计算特征点的粗匹配结果,表 2统计了正确匹配点个数、计算时间和均方根误差。本文方法不但改进了高分辨率遥感影像上特征点分布过密导致错匹配的问题,同时也有效地提升了算法的粗匹配效率,节约了计算时间。
|
|
表 2 特征点提取效率对比 Table 2 Comparison of feature point extraction number efficiency |
为验证本文方法在遥感影像配准中的有效性和可行性,在实验3中使用本文方法分别与SIFT+ST方法、SIFT+FSC方法[19]和PSO-SIFT方法[20]处理4组影像,并统计各方法的正确匹配率(correct match rate, CMR)、坏点个数(bad point proportion with norm higher than 1.5, BBP(1.5))均方根误差、算法计算总耗时t。其中SIFT+ST方法、SIFT+FSC方法、PSO-SIFT方法和本文方法的参数d为最、次临近比值筛选阈值。SIFT+ST方法的参数n为将影像标准分区为n×n的块。PSO-SIFT方法的参数dr为使用位置比例尺欧式距离(position scale orientation euclidean distance, PSOED)测量时的最、次临近比值阈值。其取值均按照原文中建议值设定。本文方法的阈值K为粗匹配点初始分组的大小,ε为计算倾向集时的判断阈值。
| $ \operatorname{CMR}=n / N . $ | (15) |
式中: CMR为控制点匹配的正确率,通过选取N组控制点,观察其中正确的n组匹配,计算比值得到正确的匹配点率。实验中每次随机取20组点,计算这20组点的匹配正确率并重复随机取点10次,得到10次结果的平均值进行汇总、比对。
| $ \text { RMSE }=\sqrt{\frac{\sum\nolimits_{i=1}^n\left[\left(x_i-x_{i^{\prime}}\right)^2+\left(y_i-y_{i^{\prime}}\right)^2\right]}{n}} . $ | (16) |
RMSE定义为带权残差平方和的平均数的平方根,作为在一定条件下衡量测量精度的一种数值指标。式(16)中的xi′和yi′代表经过变换后的校正影像上随机选取的控制点横、纵坐标,xi和yi代表控制点在基准图上的横、纵坐标。实验中随机取20组控制点,计算控制点的均方根误差,并重复随机取点20次,将20次的计算结果求平均值,得到均方根误差结果。
将使用本文方法配准后的影像叠加在参考影像上显示,得到图 5。

|
Download:
|
| 图 5 配准后影像在参考影像上叠加 Fig. 5 Superposition of registered images and reference images | |
将图 5(a)~5(d)中所示红框标选的部分截取,并放大显示,得到图 6。其中图 6(a1~a4)、6(b1~b4)、6(c1~c4)、6(d1~d4)分别代表影像1~4使用不同方法配准得到的局部匹配效果。

|
Download:
|
| 图 6 各方法叠加图局部区域效果对比 Fig. 6 Comparison of the local area in the overlay map of each method | |
第1组实验数据以农田地区为主,影像范围小、地形平坦、不同区域纹理复杂程度基本一致,SIFT+ST方法、SIFT+FSC方法和PSO-SIFT方法以及本文方法都取得了较好的配准结果,由表 3所示配准误差在1个像元以内,且耗时相差不大。SIFT+FSC通过改进随机抽样的方法,相较于原方法降低了时间复杂度。在地物丰富程度较低的影像上,本文方法通过提取精度更高的特征点,有效减少了聚类过程中的时间消耗,使得总体时间消耗增幅不明显。
|
|
表 3 不同方法评价指标的对比 Table 3 Comparison of evaluation indexes of different methods |
第2组实验数据以山地地形为主,影像范围较大,不同区域纹理复杂程度有一定差异且成像过程易受地形起伏等因素影响,导致影像中实际存在多种复杂的变换关系。SIFT+ST方法是在SIFT方法的基础上将影像均分为n×n的子影像,可以一定程度上解决局部拟合失真问题。但由于其分块方式没有考虑影像中地物的实际分布,导致其配准效果出现了偏差,对于山脊线的拟合没有对齐。SIFT+FSC方法利用快速抽样一致性的方法结合正确匹配迭代选择(iterative selection of correct matches, ISCM)方法提取了较多正确匹配;PSO-SIFT方法通过新的梯度定义方法,增加了正确匹配对的数量。这2种方法取得了较高的匹配正确率。但配准后影像在局部区域出现如图 6(b2~b3)中局部放大图所示的配准偏差,对于山脊线的走向没有正确对齐。而本文方法在同一区域如图 6(b4)所示,正确拟合了山脊线的走向,取得了更好的配准效果。在对影像2的实验中SIFT+FSC和PSO-SIFT方法以及本文方法的耗时相差不大;SIFT+FSC通过改进随机抽样的方法,相较于原方法降低了时间复杂度;PSO-SIFT方法在本文条件下增加了匹配时的判断过程,故相较原方法耗时增加,与本文O(n2)的增加程度相差不大。本文方法的BBP(1.5)数值也远低于另外几种方法,这说明本文提取的匹配点中,坏点较少,筛选能力较强。综合4种指标结果,本文方法对影像2的配准结果相对于另外3种方法有比较大的提升。
第3组实验数据包含沿海城镇区域、海洋以及海边岛屿,地物类型丰富,不同区域纹理复杂程度有很大差异,影像不同区域存在不同的变换模型。SIFT+FSC和PSO-SIFT方法得到了足够数量的配准点,但无法正确计算影像中不同区域的变换模型,没有正确拟合岛屿的变换情况,如图 6(c2~c3)所示在岛屿区域产生了1~3个像素的误差。其BBP(1.5)的统计数据也相对较高,说明其方法提取了许多坏点,影响了配准精度。如图 5(c)和图 6(c4)所示,本文的方法通过子区域划分,精确地拟合了图像每个部分的真实变换情况。SIFT+ST的方法也在图 5(c1)的区域取得较好的目视匹配效果,但根据表 3中RMSE的统计值可知,在其他地区该方法的匹配效果相对较差,原因在于该方法没有考虑影像中不同模型的实际分布情况,在某些区域的分区结果是错误的。另外该方法在时间效率上,在原有算法基础上增加了O(n2)的复杂度,而本文方法只在原有基础上增加O(K)的复杂度,相对节省了时间效率。综合各指标结果,本文方法相对于另外3种方法在影像3的配准上有较大的优势。
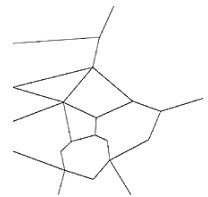
第4组实验数据为一景完整的全色遥感影像,其地物类型比较丰富,数据量大。SIFT+FSC方法由于缺乏对局部区域拟合失真的处理手段,虽然耗时较低,但其目视匹配效果较差,统计结果RMSE>4,匹配失败在表 3中以“/”表示,其目视匹配效果也如图 6(d2)所示,出现了非常大的偏差。PSO-SIFT增加了特征点匹配时的判断条件,增强了配准的鲁棒性,但缺少对局部区域拟合方法的特殊考虑,在地物类型丰富的影像上表现不佳,目视匹配效果出现如图 6(d3)所示,大约3~5个像素的偏差。SIFT+ST方法受限于其固定的分区方式,部分子区域中仍存在地物种类丰富、地形起伏大的问题。虽在选定区域目视效果较好,但在整幅影像上统计的RMSE数值较高,匹配正确率下降,整体配准效果一般。且由于分区后子区域较多、特征点数量大,导致其算法耗时大幅增加。其BBP(1.5)统计量也显著增加,说明在大范围影像上该方法提取了更多坏点。本文方法考虑了地物丰富的遥感影像局部区域存在不同拟合模型的问题。如图 7所示,算法自动地根据影像中实际变换模型的位置将影像分为13个子区域,得到较好的目视匹配效果、较高的匹配正确率且RMSE在几种方法中最低。算法的时间效率增幅比较平稳,在增大处理的数据量时,耗时增幅相对其他方法较少。
|
Download:
|
| 图 7 影像4多边形划分结果 Fig. 7 Polygon division result of image 4 | |
综合实验结果可以看出本文提出的通过层次聚类方法分析匹配点对不同变换模型的符合程度,将影像区域快速划分,完成配准的方法可以在多模型复杂变换的场景下取得比目前常用算法更优的配准效果。
3 结束语针对传统的SIFT+RANSAC的配准方法在处理高分辨率影像时由于地形起伏、地物类型丰富等问题无法正确精细拟合影像局部区域,导致影像配准效果不佳的问题,本文引入基于J-Linkage的层次聚类方法。通过特征点的邻域信息,将点划分为组,并生成变换模型,计算每个匹配点与不同模型的符合程度,生成匹配点的模型倾向集,最后通过Jaccard距离将倾向集合并,得到聚类结果并根据聚类中心划分影像范围。分组结果理论上模拟了影像中局部模型的真实分布情况,可以消除使用全局模型进行配准带来的局部失真问题。文中通过实验验证了在进行高分辨率遥感影像配准时,相对目前常用的SIFT+ST方法、SIFT+FSC方法和PSO-SIFT方法,本文提出的方法可以取得更好的配准效果。本文的研究重点为根据特征信息对影像进行快速准确的区域划分,但在某些情况下,划分之后的区域仍然需要更准确的错误关系剔除方法以及更精细的拟合模型来提高配准效果,这将是未来的研究方向和需要解决的问题。
| [1] |
潘腾. 高分二号卫星的技术特点[J]. 中国航天, 2015(1): 3-9. |
| [2] |
Lowe D G. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision, 2004, 60(2): 91-110. Doi:10.1023/b:visi.0000029664.99615.94 |
| [3] |
Yan X H, Zhang Y J, Zhang D J, et al. Registration of multimodal remote sensing images using transfer optimization[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(12): 2060-2064. Doi:10.1109/LGRS.2019.2963477 |
| [4] |
Jiang X Y, Ma J Y, Fan A X, et al. Robust feature matching for remote sensing image registration via linear adaptive filtering[J]. IEEE Transactions on Geoscience and Remote Sensing, 2021, 59(2): 1577-1591. Doi:10.1109/TGRS.2020.3001089 |
| [5] |
Zhang T, Zhao R, Chen Z S. Application of migration image registration algorithm based on improved SURF in remote sensing image mosaic[J]. IEEE Access, 2020, 8: 163637-163645. Doi:10.1109/ACCESS.2020.3020808 |
| [6] |
Sedaghat A, Mohammadi N. Illumination-Robust remote sensing image matching based on oriented self-similarity[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2019, 153: 21-35. Doi:10.1016/j.isprsjprs.2019.04.018 |
| [7] |
Ma X K, Zhao W J, Hao X Y, et al. Remote sensing image registration with adjustable threshold and variational mixture transformation[J]. IEEE Geoscience and Remote Sensing Letters, 2020, 17(5): 765-769. Doi:10.1109/LGRS.2019.2936396 |
| [8] |
Yang H, Li X R, Zhao L Y, et al. A novel coarse-to-fine scheme for remote sensing image registration based on SIFT and phase correlation[J]. Remote Sensing, 2019, 11(15): 1833. Doi:10.3390/rs11151833 |
| [9] |
Zhang H P, Leng C C, Yan X, et al. Remote sensing image registration based on local affine constraint with circle descriptor[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1-5. Doi:10.1109/LGRS.2020.3027096 |
| [10] |
Liu Z Q, Wang L C, Wang X M, et al. Secure remote sensing image registration based on compressed sensing in cloud setting[J]. IEEE Access, 2019, 7: 36516-36526. Doi:10.1109/ACCESS.2019.2903826 |
| [11] |
Zhang J, Ma W P, Wu Y, et al. Multimodal remote sensing image registration based on image transfer and local features[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(8): 1210-1214. Doi:10.1109/LGRS.2019.2896341 |
| [12] |
Zhou C, Zhang G, Yang Z F, et al. A novel image registration algorithm using wavelet transform and matrix-multiply discrete Fourier transform[J]. IEEE Geoscience and Remote Sensing Letters, 2022, 19: 1-5. Doi:10.1109/LGRS.2020.3031335 |
| [13] |
冯蕊涛, 杜清运, 罗恒, 等. 基于光流校正的复杂地形区多时相遥感影像配准[J]. 遥感学报, 2021, 25(2): 630-640. Doi:10.11834/jrs.20209280 |
| [14] |
王慧贤, 靳惠佳, 雷呈强, 等. 视觉驱动的变分配准方法[J]. 测绘学报, 2015, 44(8): 893-899. Doi:10.11947/j.AGCS.2015.20140281 |
| [15] |
Zaragoza J, Chin T J, Tran Q H, et al. As-projective-as-possible image stitching with moving DLT[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2014, 36(7): 1285-1298. Doi:10.1109/TPAMI.2013.247 |
| [16] |
Toldo R, Fusiello A. Robust multiple structures estimation with J-linkage[M]//Lecture Notes in Computer Science. Berlin, Heidelberg: Springer Berlin Heidelberg, 2008: 537-547. DOI: 10.1007/978-3-540-88682-2_41.
|
| [17] |
凌霄. 基于多重约束的多源光学卫星影像自动匹配方法研究[D]. 武汉: 武汉大学, 2017.
|
| [18] |
Arandjelović R, Zisserman A. Three things everyone should know to improve object retrieval[C]//2012 IEEE Conference on Computer Vision and Pattern Recognition. June 16-21, 2012, Providence, RI, USA. IEEE, 2012: 2911-2918. DOI: 10.1109/CVPR.2012.6248018.
|
| [19] |
Wu Y, Ma W P, Gong M G, et al. A novel point-matching algorithm based on fast sample consensus for image registration[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(1): 43-47. Doi:10.1109/LGRS.2014.2325970 |
| [20] |
Ma W P, Wen Z L, Wu Y, et al. Remote sensing image registration with modified SIFT and enhanced feature matching[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(1): 3-7. Doi:10.1109/LGRS.2016.2600858 |
 2024, Vol. 41
2024, Vol. 41 


