2. 中国科学院大学电子电气与通信工程学院, 北京 100049
2. School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 100049, China
波束形成是相控阵天线领域中的一个重要研究方向,广泛应用于电子对抗、合成孔径雷达(synthetic aperture radar, SAR)成像[1-2]以及5G通信领域[3]。进入21世纪之后,有源相控阵天线技术的发展使多功能雷达的实现成为可能。多功能雷达要求天线在不同的应用场景下可以形成不同的波束方向图,其中余割平方和平顶波束方向图是两种常见的方向图。对某些雷达而言通常要求俯仰方向上的天线方向图呈现余割平方的形式,以此实现不同距离目标到达雷达接收机的信号功率相同。而平顶波束方向图可以保证在一定角度范围内接收到的信号功率是均匀一致且旁瓣电平可控的[4]。在形成波束方向图的同时,为提高雷达的抗干扰能力同时减少来波信号估计的难度,通常会在干扰信号附近生成一个宽零陷。基于以上想法本文采用联合优化算法设计了带宽零陷的波束方向图。
波束形成的最终目的是找到合适的阵元加权值以产生所需的辐射方向图。寻找加权值的算法有很多,主要分为3大类:数值优化算法、智能优化算法,及联合优化算法。数值优化算法包括离散傅里叶变换、Dolph_Chebychev综合[5]、Taylor综合[6]、Wood-wards算法[7],及其他算法[8-9]。传统优化算法可以准确快速地得到简单模型的赋形结果,但对于多参数多目标问题无法得到准确的解。智能优化算法主要包括遗传算法(genetic algorithm,GA)、粒子群算法、蚁群算法、模拟退火算法、免疫算法等。这些算法主要是通过模拟自然界中生物或者自然现象的智能行为提出来的,智能优化算法适用于多参数优化的问题,且不受优化函数梯度不存在的困扰,但标准的智能优化算法收敛速度慢,容易陷入局部最优点,因此大量的学者对智能优化算法进行了改进[10-12]。联合优化算法通过将两种及以上的算法进行结合,能够克服单一算法优化存在的弊端,具有较好的结果[13-15]。
本文提出一种新的联合优化算法,将快速逆傅里叶变换(inverse fast Fourier transform,IFFT)和遗传算法相结合,最终生成复杂的带宽零陷的波束方向图。算法基于天线方向图与阵元电流的傅里叶变换关系,对于目标波束方向图,利用IFFT得到每个阵元的加权值。将得到的阵元幅度和相位值作为遗传算法的初始值然后通过改进的遗传算法(improved genetic algorithm,IGA)生成带宽零陷的波束方向图,同时对旁瓣电平、零陷深度和主波束的波纹进行约束。在生成波束方向图中的宽零陷时采用唯相加权的方法,与同时对幅度和相位进行加权(或者仅对幅度进行加权)[13, 16]以及对天线位置进行加权[17]相比,唯相加权[18]能够有效减少天线的机械设计难度,简化天线的馈线设计,同时可以通过改变T/R组件中的移相值,在不同位置处生成宽零陷,提高雷达的抗干扰能力。文献[12]采用改进的粒子群算法通过对阵元进行相位加权形成宽零陷。文献[19]采用唯相加权降低波束方向图的副瓣。文献[20]将波束形成转化为求解方程组的问题,在已知阵元幅度权值的条件下,通过求解方程组得到阵元的相位分布,最终形成余割平方和平顶波束方向图。文献[21]在唯相加权的约束下,对比了粒子群算法、模拟退火算法和遗传算法在实现波束展宽的结果。文献[22]中提出了3种改进的傅里叶变换方法,通过唯相加权实现了子阵级别的波束展宽。
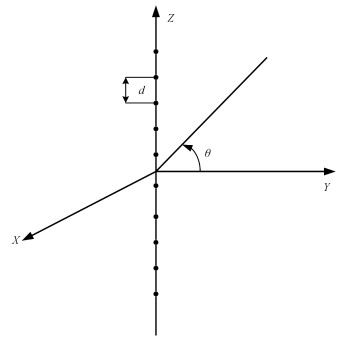
1 波束形成原理及算法 1.1 基于傅里叶变换的波束形成原理傅里叶变换是时频分析的经典方法,在信号处理领域具有广泛应用,对于电磁场和天线来说,天线的波束方向图与天线阵元电流分布存在傅里叶变换的关系,因此如果已知天线的波束方向图就可以通过IFFT快速得到天线阵元的权值。图 1所示为天线阵元的结构图,全向天线阵元沿Z轴排布,波束指向为Y轴方向。
| $ \boldsymbol{B}_{\theta}(\theta)=\boldsymbol{\omega}^{\mathrm{H}} \boldsymbol{v}_{\theta}=\sum\limits_{n=0}^{N-1} \boldsymbol{\omega}_{n}^{*} \mathrm{e}^{\mathrm{j}\left(n-\frac{N-1}{2}\right) \frac{2 {\rm{ \mathsf{ π}}} d}{\lambda}(\sin \theta+\sin \bar{\theta})} . $ | (1) |
|
Download:
|
| 图 1 线性阵列阵元位置图 Fig. 1 Linear array element location | |
式(1)给出的是远场方向图,其中-0.5π≤θ≤0.5π,ω为天线单元的权值(包含幅度值和相位值),vθ为θ空间中的阵列流形矢量,N为阵列天线的单元数目,d为天线单元间距,λ为波长,θ是相对于Z轴法线方向的极角,θ是波束方向图的扫描角,n为天线单元的位置标号,H表示对矩阵求转置共轭,*表示对矩阵求共轭。
根据天线方向图与阵元电流之间的傅里叶变换关系,用IFFT生成波束方向图的具体推导在文献[23]中已经给出,在此仅给出关键步骤,初始时未进行波束扫描,波束指向为阵列法线方向。
| $ \mu_{k}=\left(k-\frac{N-1}{2}+\Delta N\right) \frac{\lambda}{N d} ; k=0, 1, \cdots, N-1 . $ | (2) |
式(2)是采样点的位置,其中μ=sinθ,ΔN∈[0, 1] 用来对采样点的位置进行微调,使采样值更加准确。
| $ B(k)=B_{\mu}^{*}\left(\mu_{k}\right) \mathrm{e}^{-\mathrm{j} \mu_{k}\left(\frac{N-1}{2}\right)}, $ | (3) |
| $ b_{n}=\operatorname{IDFT}(B(k))=\frac{1}{N} \sum\limits_{k=0}^{N-1} B(k) \mathrm{e}^{\mathrm{j} k n \frac{2 {\rm{ \mathsf{ π}}}}{N}}, $ | (4) |
| $ \omega_{n}=b_{n} \mathrm{e}^{-\mathrm{j} n {\rm{ \mathsf{ π}}}\left(\frac{N-1}{N}\right)}, $ | (5) |
所以B(k)与bn是一对离散傅里叶变换的关系,借助这一关系,通过式(2)~式(5)对目标方向图进行逆离散傅里叶变换(inverse discrete Fourier transform,IDFT)即可得到主波束方向图的阵元加权值ω。
因为IFFT能加快傅里叶变换的速度,因此在实际计算过程中采用IFFT实现IDFT。
1.2 IGA原理遗传算法是一种自适应的全局优化算法,能够有效地解决非线性、多目标的优化问题。算法的主要步骤包括:编码及初始化种群,选择运算,交叉运算,变异运算。主要的参数包括种群规模NP,交叉概率Pc,遗传进化的迭代次数G等。标准的遗传算法搜索能力较差,容易陷入局部最优,因此在本文的工作中通过引入混沌映射来改进标准的遗传算法,算法的具体步骤如下:
1) 编码及初始化种群
本文的变量为连续变量,因此采用实数编码。设置种群规模为NP,初始种群中第i个个体的染色体为Fi,对染色体进行基因编码Fi=[fi1, fi2, …, fiN], i = 1, 2, …, NP,N为基因数量(也就是阵列天线的单元数目);设置进化迭代的代数G,交叉概率Pc,加权相位的下限Xmin,上限Xmax。
引入Sinusoidal混沌映射进行种群的初始化,借助混沌映射的遍历性和随机性增强种群的多样性。
| $ \boldsymbol{F}_{i+1}=\alpha \cdot \boldsymbol{F}_{i}^{2} \cdot \sin \left(\boldsymbol{F}_{i} \cdot {\rm{ \mathsf{ π}}}\right) ; \boldsymbol{F}_{i} \in[0, 1], $ | (6) |
| $ \boldsymbol{F}_{1}=\operatorname{rand}(N, 1), $ | (7) |
| $ \boldsymbol{F}_{i}=\boldsymbol{F}_{i} \cdot\left(X_{\max }-X_{\min }\right)+X_{\min }, $ | (8) |
其中,α为混沌映射系数,i=1, 2, …, NP。然后通过式(8)将每个个体的基因约束到加权相位的范围之中。
2) 选择和交叉操作
① 选择操作
通过构造的适应度函数Fit计算个体的适应度,将个体按适应度优劣进行排序,选择最优良的个体作为“君主”。
② 交叉操作
将第k代中最优的“君主”与第k代中所有的偶数位个体都进行交叉操作,交叉概率为Pc,得到第k代的子代NFik,子代中的奇数位个体为第k代的“君主”个体。
3) 变异操作
① 变异操作
将第2步中得到的子代个体NFik=[nfi1k, nfi2k, …, nfiNk] 引入混沌扰动实现变异操作
| $ \boldsymbol{N} \boldsymbol{F}_{i}^{k}=\boldsymbol{N} \boldsymbol{F}_{i}^{k}+\gamma \cdot\left({\bf{\Delta}} \boldsymbol{N} \boldsymbol{F}_{i}^{k}-0.5\right), $ | (9) |
其中ΔNFik是采用Sinusoidal混沌映射所生成,γ是个体基因变异的控制系数。在遗传算法进化的初期,γ值应该较大以提高搜索效率,在算法的后期γ应该取值较小以提高搜索的精度,因此γ的选择应该和进化的代数k有关,如下所示。
| $ \gamma=\mathrm{e}^{\frac{-\beta(k-1)}{G}}, $ | (10) |
其中:G为进化的总代数,k为当前进化的代数,β为控制空间搜索的尺度。
② 边界吸收
在变异中引入混沌扰动之后会有部分个体的基因超过加权相位的上下限,因此需要对变异之后的子代个体基因进行约束,采用边界吸收的方法实现对子代基因的约束。
| $ n f_{i j}^{k}=\left\{\begin{array}{l} n f_{i j}^{k}, X_{\min } \leqslant n f_{i j}^{k} \leqslant X_{\max }, \\ X_{\min }, n f_{i j}^{k}<X_{\min }, \\ X_{\max }, n f_{i j}^{k}>X_{\max } . \end{array}\right. $ | (11) |
③ 生成新一代种群
用适应度函数Fit计算子代NFik的适应度,将其与父代Fik合并之后选择最优的NP个个体作为新一代种群Fik+1,由此完成一次遗传与进化。
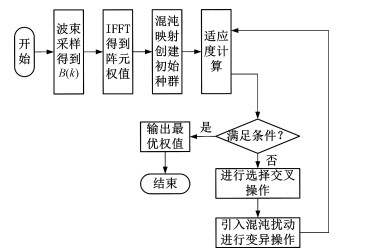
1.3 联合优化算法数学模型本文的联合优化算法通过将IFFT和IGA相结合来实现,最终目的是得到带宽零陷的波束方向图,其中宽零陷的生成采用唯相加权的方法实现。算法的框架如图 2所示。
|
Download:
|
| 图 2 本文联合优化算法框架 Fig. 2 Framework of the proposed combined algorithm | |
适应度函数的选取需要考虑宽零陷的生成、零陷深度、波束方向图的旁瓣电平以及波束方向图主瓣上的波动。
| $ { Fit }=a_{1} \sum\limits_{\theta=-90}^{90}\left(\boldsymbol{W}_{\text {null }} \cdot \boldsymbol{B}_{\omega}-\boldsymbol{B}_{d}\right)^{2}+F, $ | (12) |
| $ \begin{gathered} F=a_{2} \operatorname{sum}\left(\boldsymbol{f}_{2}\right)+a_{3} \operatorname{sum}\left(\boldsymbol{f}_{3}\right)+ \\ a_{4} \operatorname{sum}\left(\boldsymbol{f}_{4}\right)+a_{5} \operatorname{sum}\left(\boldsymbol{f}_{5}\right), \end{gathered} $ | (13) |
本文中的适应度函数如式(12)、式(13)所示,其中:Fit为遗传算法中的适应度函数;Bω是通过IFFT后得到的主波束方向图;Bd是理想的波束方向图,用于对波束方向图的整体进行约束;f2为左旁瓣约束,f3为右旁瓣约束,f4为宽零陷约束,f5为主波束上的波动约束;a1,a2,a3,a4,a5为调整不同约束的权值。
2 仿真实现为验证本文算法的有效性,采用Matlab对2种赋形波束进行仿真。目标是生成主波束位于[0°, 25°]带宽零陷的余割平方波束方向图和主波束位于[-15°, 15°]带宽零陷的平顶波束方向图。零陷所在范围为[-60°,-45°],零陷深度低于-50 dB,旁瓣电平低于-18 dB,主瓣波动小,生成的波束方向图能够实现快速扫描。将本文算法结果与采用标准GA与IFFT结合的传统联合优化算法(traditional combined algorithm, TCA)得到的仿真结果进行比较。仿真参数如表 1。
|
|
表 1 仿真参数 Table 1 Simulation parameters |
余割平方函数的表达式为
| $ f_{1}(\theta)=\left\{\begin{array}{l} \frac{\csc ^{2}\left(\theta+18^{\circ}\right)}{\csc ^{2}\left(18^{\circ}\right)}, \theta \in\left[0^{\circ}, 25^{\circ}\right] ,\\ 0, \theta \in \text { otherwise. } \end{array}\right. $ | (14) |
用于生成宽零陷的函数Wnull的表达式如下
| $ W_{\text {null }}(\theta)=\left\{\begin{array}{l} 50, \theta \in\left[-60^{\circ}, -45^{\circ}\right], \\ 100, \theta \in \text { otherwise. } \end{array}\right. $$ $ | (15) |
Bd是理想的最终波束方向图
| $ B_{d}(\theta)=\left\{\begin{array}{l} 20 \lg \frac{\csc ^{2}\left(\theta+18^{\circ}\right)}{\csc ^{2}\left(18^{\circ}\right)}, \theta \in\left[0^{\circ}, 25^{\circ}\right], \\ -60 \mathrm{~dB}, \theta \in\left[-60^{\circ}, -45^{\circ}\right], \\ -21 \mathrm{~dB}, \theta \in \text { otherwise. } \end{array}\right. $ | (16) |
在对波束方向图的旁瓣和零陷深度进行约束的过程中,由于IFFT生成波束方向图时主波束略有展宽,因此左旁瓣范围为[-90°,-3°],右旁瓣范围为[25°, 90°],下面给出几个约束函数的表达式。
| $ \begin{array}{l} {f_2}(\theta ) = \left\{ {\begin{array}{*{20}{l}} {2, }&{{f_2}(\theta ) > - 21\;{\rm{dB}}, }\\ {0, }&{{\rm{ otherwise}}{\rm{. }}} \end{array}} \right.\\ \theta \in \left[ { - {{90}^\circ }, - {{60}^\circ }} \right] \cup \left[ { - {{45}^\circ }, - {3^\circ }} \right], \end{array} $ | (17) |
| $ {f_3}(\theta ) = \left\{ {\begin{array}{*{20}{l}} {2, }&{{f_3}(\theta ) > - 21\;{\rm{dB}}, }\\ {0, }&{{\rm{ otherwise }};} \end{array} \theta \in \left[ {{{25}^\circ }, {{90}^\circ }} \right], } \right. $ | (18) |
| $ {f_4}(\theta ) = \left\{ {\begin{array}{*{20}{l}} {2, }&{{f_4}(\theta ) > - 60\;{\rm{dB}}, }\\ {0, }&{{\rm{ otherwise }};} \end{array}\quad \theta \in \left[ { - {{60}^\circ }, - {{45}^\circ }} \right], } \right. $ | (19) |
| $ \begin{array}{l} {f_5}(\theta ) = \\ \left\{ {\begin{array}{*{20}{l}} {\left| {{W_{{\rm{null }}}}(\theta ) \cdot {B_\omega }(\theta ) - {B_d}(\theta )} \right|, \theta \in \left[ { - {3^\circ }, {{25}^\circ }} \right], }\\ {0, {\rm{ otherwise}}{\rm{. }}} \end{array}} \right. \end{array} $ | (20) |
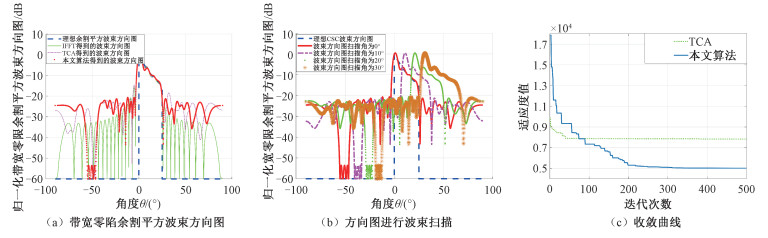
调节a1~a5的值可以生成所需的波束方向图,得到的结果如图 3和图 4所示。
|
Download:
|
| 图 3 带宽零陷的余割平方波束方向图仿真结果 Fig. 3 Simulation results of cosecant square beam pattern with wide null | |
|
Download:
|
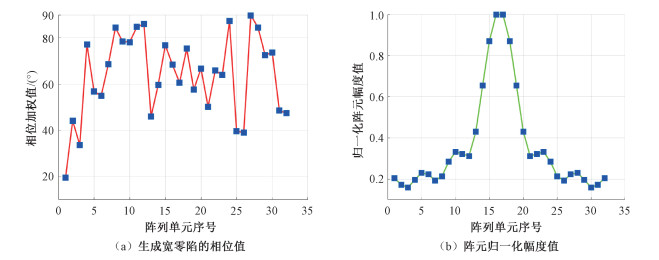
| 图 4 余割平方波束方向图天线单元的相位值和归一化幅度值 Fig. 4 Phase and normalized amplitude value of antenna unit for cosecant square beam pattern | |
表 2给出两种算法生成的带宽零陷余割平方波束方向图的仿真结果对比,可以看到本文算法生成的波束方向图最大旁瓣水平(maximum side lobe level,MSLL)为-20.63 dB,-50 dB零陷宽度(null width, NW)为9.74°,迭代收敛次数为332次,均优于TCA,最大主瓣波动(maximum main lobe fluctuation,MMLF)与TCA相比略有增长。从图 3(c)的收敛曲线中可以看到本文算法跳出了局部最优值,可以得到更好的结果。图 3(b)给出波束方向图扫描10°、20°、30°的结果,从图中可以看到波束扫描不会破坏波形的整体情况,但会展宽波束方向图。图 4给出余割平方波束方向图生成宽零陷的相位值以及IFFT后阵元的归一化幅度值。
|
|
表 2 带宽零陷余割平方波束方向图结果对比 Table 2 Comparison of cosecant square beam pattern with wide null |
与生成带宽零陷的余割平方波束方向图的过程类似,通过设置主波束方向图f1为平顶波束,调整主波束的范围,并适当调节约束函数,可以得到带宽零陷的平顶波束方向图,其结果如图 5和图 6所示。
|
Download:
|
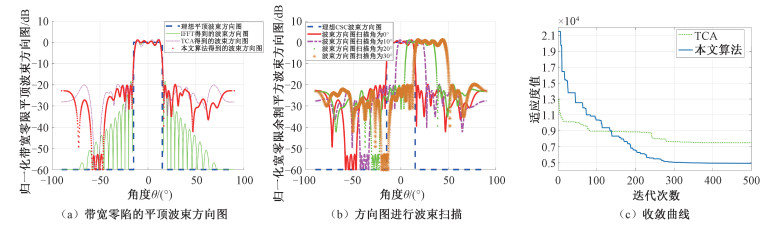
| 图 5 带宽零陷的平顶波束方向图仿真结果 Fig. 5 Simulation results of flat-top beam pattern with wide null | |
|
Download:
|
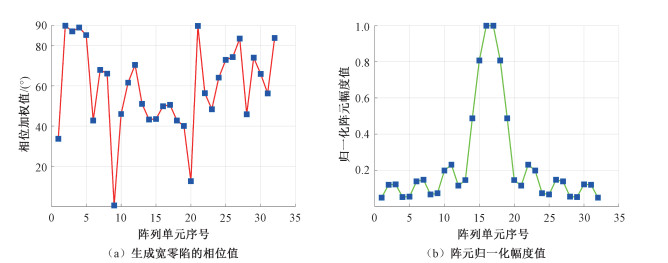
| 图 6 平顶波束方向图天线单元的相位值和归一化幅度值 Fig. 6 Phase and normalized amplitude value of antenna unit for flat-top beam pattern | |
从表 3给出的结果不难看出,在生成带宽零陷的平顶波束方向图时,本文算法在最大旁瓣水平、最大主瓣波动、-50 dB零陷宽度上均优于TCA,但迭代收敛次数略高于TCA。分析图 5(c)的收敛曲线可以发现,尽管TCA收敛时迭代的次数小于本文算法,但其结果并不能满足宽零陷的要求,这表明TCA陷入了局部最优值,从而导致算法过早收敛。图 5(b)给出平顶波束扫描的仿真,结果同样表明除波束方向图发生展宽之外波束的整体情况并不会因为进行波束扫描而被破坏。图 6给出平顶波束生成宽零陷的相位加权值,以及IFFT后得到的阵元归一化幅度值。
|
|
表 3 带宽零陷平顶波束方向图结果对比 Table 3 Comparison of flat-top beam pattern with wide null |
综上所述,本文算法在生成带宽零陷的复杂波束方向图时,在最大旁瓣水平、最大主瓣波动以及零陷宽度上均有改善,并且算法收敛时迭代的次数较少,在保证收敛快速的同时可以得到更好的结果,得到的结果可以进行快速波束扫描且不会破坏波束的整体形状。
3 结论本文提出一种新的联合优化算法,该算法通过将IFFT和IGA相结合生成带宽零陷的复杂波束方向图,其中宽零陷的生成采用唯相加权的方法,算法中引入Sinusoidal混沌映射来增加种群的多样性,并在变异过程中引入混沌扰动。通过对2种不同波束方向图的仿真结果显示,本文提出的算法与TCA相比有明显的改善,且在迭代500次以内即可得到满足要求的结果,在一定程度上解决了复杂波束形成时收敛速度慢、容易陷入局部最优的问题。
| [1] |
刘海廷, 吕晓德. 一种改善SAR距离模糊的天线赋形算法[J]. 中国科学院研究生院学报, 2009, 26(1): 102-106. Doi:10.7523/j.issn.2095-6134.2009.1.015 |
| [2] |
杨俊, 王建峰, 乞耀龙, 等. 基于波束形成原理SAR三维成像算法[J]. 中国科学院大学学报, 2016, 33(1): 115-120. Doi:10.7523/j.issn.2095-6134.2016.01.017 |
| [3] |
殷锋, 邱玲, 梁晓雯. 多用户毫米波大规模MIMO系统中收发端联合的混合波束成形设计[J]. 中国科学院大学学报, 2021, 38(2): 252-259. Doi:10.7523/j.issn.2095-6134.2021.02.011 |
| [4] |
陈诚, 黄卡玛. 无线能量传输中平顶波束的分析应用[J]. 电子与信息学报, 2018, 40(5): 1115-1121. Doi:10.11999/JEIT170710 |
| [5] |
Dolph C L. A current distribution for broadside arrays which optimizes the relationship between beam width and side-lobe level[J]. Proceedings of the IRE, 1946, 34(6): 335-348. Doi:10.1109/JRPROC.1946.225956 |
| [6] |
Taylor T T. Design of line-source antennas for narrow beamwidth and low side lobes[J]. Transactions of the IRE Professional Group on Antennas and Propagation, 1955, 3(1): 16-28. Doi:10.1109/TPGAP.1955.5720407 |
| [7] |
Woodward P M. A method of calculating the field over a plane aperture required to produce a given polar diagram[J]. Journal of the Institution of Electrical Engineers-Part ⅢA: Radiolocation, 1946, 93(10): 1554-1558. Doi:10.1049/ji-3a-1.1946.0262 |
| [8] |
Gatti R V, Marcaccioli L, Sorrentino R. A novel phase-only method for shaped beam synthesis and adaptive nulling[C]//200333rd European Microwave Conference. October 2-10, 2003, Munich, Germany. IEEE, 2003: 739-742. DOI: 10.1109/EUMA.2003.341059.
|
| [9] |
杜海龙, 闫鲁滨. 一种唯相波束赋形的快速方法[J]. 宇航学报, 2010, 31(6): 1608-1612. Doi:10.3873/j.issn.1000-1328.2010.06.016 |
| [10] |
Yan K K, Lu Y L. Sidelobe reduction in array-pattern synthesis using genetic algorithm[J]. IEEE Transactions on Antennas and Propagation, 1997, 45(7): 1117-1122. Doi:10.1109/8.596902 |
| [11] |
Kenane E H, Djahli F, Dumond C. A novel modified invasive weeds optimization for linear array antennas nulls control[C]//20154th International Conference on Electrical Engineering (ICEE). December 13-15, 2015, Boumerdes, Algeria. IEEE, 2015: 1-4. DOI: 10.1109/INTEE.2015.7416784.
|
| [12] |
周强锋. 基于仅相位加权的宽零陷低副瓣波束赋形方法[J]. 现代防御技术, 2019, 47(4): 59-64. Doi:10.3969/j.issn.1009-086x.2019.04.10 |
| [13] |
Gao Z G, Yang B. Antenna pattern synthesis of shaped-beam using a new combined algorithm[C]//Proceedings of 20143rd Asia-Pacific Conference on Antennas and Propagation. July 26-29, 2014, Harbin, China. IEEE, 2014: 291-293. DOI: 10.1109/APCAP.2014.6992477.
|
| [14] |
丛友记, 卞美琴, 简玲. 一种唯相位加权降低天线副瓣技术研究[J]. 雷达与对抗, 2015, 35(2): 45-48. Doi:10.19341/j.cnki.issn.1009-0401.2015.02.012 |
| [15] |
徐慧, 李建新, 胡明春. 星载SAR波束展宽研究[J]. 电子与信息学报, 2007, 29(3): 540-543. |
| [16] |
Mandal D, Kumar R, Kar R, et al. Wide nulls control of linear antenna arrays using craziness based particle swarm optimization[C]//2011 IEEE Student Conference on Research and Development. December 19-20, 2011, Cyberjaya, Malaysia. IEEE, 2011: 189-193. DOI: 10.1109/SCOReD.2011.6148733.
|
| [17] |
Kumari P, Mitra E, Mandal D. Wide null control of compact multiple antenna terminals using PSO[C]//2017 International Electrical Engineering Congress (iEECON). March 8-10, 2017, Pattaya, Thailand. IEEE, 2017: 1-5. DOI: 10.1109/IEECON.2017.8075847.
|
| [18] |
Khalaj-Amirhosseini M. Phase-only power pattern synthesis of linear arrays using autocorrelation matching method[J]. IEEE Antennas and Wireless Propagation Letters, 2019, 18(7): 1487-1491. Doi:10.1109/LAWP.2019.2920866 |
| [19] |
Harikumar P, Bikkani V V B, Mahanti G K, et al. Phase-only side lobe level reduction of uniformly excited linear array antenna using iterative Fast Fourier transform[C]//2011 Annual IEEE India Conference. December 16-18, 2011, Hyderabad, India. IEEE, 2011: 1-4. DOI: 10.1109/INDCON.2011.6139456.
|
| [20] |
Erçil E. An alternative method for phase only array pattern synthesis[C]//Proceedings of the 2012 IEEE International Symposium on Antennas and Propagation. July 8-14, 2012, Chicago, IL, USA. IEEE, 2012: 1-2. DOI: 10.1109/APS.2012.6348690.
|
| [21] |
Daniel B, Edwards C, Anderson A. Phase-only beam broadening of contiguous uniform subarrayed arrays utilizing three metaheuristic global optimization techniques[EB/OL]. arXiv: 2009.06123. (2020-09-14)[2021-12-20]. https://arxiv.org/abs/2009.06123.
|
| [22] |
Daniel B K, Anderson A L. Phase-only beam broadening of contiguous uniform subarrayed arrays[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(5): 4001-4013. Doi:10.1109/TAES.2020.2987115 |
| [23] |
第斯. 最优阵列处理技术[M]. 汤俊, 译. 北京: 清华大学出版社, 2008: 88-92.
|
 2023, Vol. 40
2023, Vol. 40 


