2021年5月22日2时4分,青海果洛州玛多县(34.59°N,98.34°E)发生MS7.4地震(图 1),震源深度17 km(中国地震台网正式测定)[1]。该地震极震区的烈度最大值为Ⅹ度,Ⅵ度及以上区域面积约为53 704 km2,宏观震中和微观震中分别为玛多县玛查理镇和黄河乡[2]。从发震构造上看,青海玛多地震发生在青藏高原中部的Ⅱ级地块巴颜喀拉块体北部,距其北边界东昆仑断裂带约70 km。近年来,巴颜喀拉块体周缘发生一系列强震,如2008年汶川8.0级地震、2011年玉树7.1级地震、2013年芦山7.0级地震、2017年九寨沟7.0级地震,而玛多地震却是唯一发生在巴颜喀拉块体内部的强震[3],因此受到科研人员的广泛关注。人们从震源机制、震源破裂过程、发震断裂、余震序列、同震滑动分布、震区构造应力场、库仑应力变化和地震危险性等方面对玛多地震进行了研究。

|
Download:
|
| F1:达日断裂带;F2:玛多—甘德断裂带;F3:东昆仑断裂带;F4:昆中断裂带;F5:鄂拉山断裂带,断层数据引自詹艳等[4]。 图 1 玛多地震的构造背景和地震活动性 Fig. 1 The tectonic setting of the Maduo earthquake and the historical seismicity in research area | |
中国地震台网、美国地质调查局等机构对此次地震的震源机制和震源破裂过程反演后认为该地震为一次左旋走滑型地震事件,兼有正断分量[4],为双侧破裂方式,震区构造应力场最大主应力轴方向为NE-SW,最小主应力轴方向为NNW-SSE[1]。李志才等[5]对GNSS数据进行反演确定的地震矩、断裂的几何参数及同震滑动分布,也揭示了发震断裂左旋走滑特性,同时得到同震滑动量的数值及分布。余震双差重定位研究发现,余震带与昆仑山口—江错断裂距离最近且两者走向有一定的重合度,说明玛多地震的发震断裂为昆仑山口—江错断裂[3, 6],与野外地震考察结果相一致[7-10]。前人对于玛多地震同震及震后变形研究可以分为大地测量数据反演及同震、震后变形及相关应力变化模拟多个方面。研究者基于InSAR、GPS等大地测量数据与图像,揭示出最大滑动量为6.0 m[11-12],并确定了同震变形、静态滑动分布以及断层破裂过程[13],量化了地震间应变率、断层几何以及同震滑动分布[14]。基于InSAR数据反演的断层滑动模型和PREM地球模型,研究者计算了此次地震的理论同震位移、大地水准面、重力及应变的变化,得到地壳变形的空间分布,为研究地震断层及解释大地测量数据提供了参考[15]。在同震、震后变形模拟及库仑应力计算方面,杨光远等[16]使用Coulomb3.3程序[17-18]计算玛多地震引起的地震破裂面及周边主要断层上的库仑应力变化;谈洪波等[19]和Li等[20]使用均匀半空间解析解PSGRN/PSCRM程序[21]对玛多地震同震、震后变形、重力变化及发震断层及周围区域的库仑应力变化进行了计算模拟。
前人使用解析法或半解析法对同震、震后及库仑应力变化进行理论计算,模型比较简单,计算速度快,因此,在大地震发生不久,通常会有相关的同震、震后及库仑应力变化成果发布,对大地震周围区域的地震危险性做出第一时间的评估和判断。发震断层周围介质的非均匀性、几何的复杂性,对大地震的同震变形影响很大,简单的解析解和半解析解很难考虑这些复杂因素,而数值模拟可以发挥独特的优势。在数值模拟中,有限元方法可以根据实际地质体的几何、材料及边界条件灵活地进行网格划分,同时进行并行计算,实现对复杂地质体高分辨率模拟。分裂节点法通过将位错加入到载荷向量而不改变刚度矩阵,可以简洁有效地将断层位错引入有限元计算。为此,本文采用C语言编写了分裂节点法的三维并行弹性有限元程序,用该程序计算了青海玛多地震的同震变形和应力变化,并对研究区域主要断层地震危险性进行探讨。
1 有限元方法 1.1 使用分裂节点法的有限元模型构建用有限元方法模拟地震变形时,首先面临的问题是如何将断层的同震位错引入有限元数值计算中。分裂节点法可以简单有效地解决该问题[22]。如图 2所示,单元1、2分别位于断层的左右两侧,U为位移,上标表示单元号,下标表示单元内的节点号;ΔU表示位错量[22]。

|
Download:
|
| 图 2 分裂节点法的示意图 Fig. 2 Schematic diagram of split node technique | |
则有
| $ U_2^1=\overline{U}_2^1+\Delta U_2^1, $ | (1) |
| $ U_1^2=\overline{U}_1^2+\Delta U_1^2 .$ | (2) |
单元1的节点2和单元2的节点1上的位移可以分为两部分,一部分是平均位移,即
| $\overline{U}_2^1=\overline{U}_1^2 .$ | (3) |
另一部分是位错量,即ΔU21、ΔU12,满足
| $\Delta U_2^1=-\Delta U_1^2 .$ | (4) |
单元1的单元刚度矩阵方程为
| $\left[\begin{array}{ll} K_{11}^1 & K_{12}^1 \\ K_{21}^1 & K_{22}^1 \end{array}\right]\left[\begin{array}{l} U_1^1 \\ \overline{U}_2^1 \end{array}\right]=\left[\begin{array}{l} F_1^1-K_{12}^1 \Delta U_2^1 \\ F_2^1-K_{22}^1 \Delta U_2^1 \end{array}\right] .$ | (5) |
同样,单元2的单元刚度矩阵方程为
| $\left[\begin{array}{ll} K_{11}^2 & K_{12}^2 \\ K_{21}^2 & K_{22}^2 \end{array}\right]\left[\begin{array}{l} \overline{U}_1^2 \\ U_2^2 \end{array}\right]=\left[\begin{array}{l} F_1^2-K_{12}^2 \Delta U_2^2 \\ F_2^2-K_{22}^2 \Delta U_2^2 \end{array}\right] .$ | (6) |
总体刚度矩阵方程为
| $\begin{array}{c} {\left[\begin{array}{ccc} K_{11}^1 & K_{12}^1 & 0 \\ K_{21}^1 & K_{22}^1+K_{11}^2 & K_{12}^2 \\ 0 & K_{21}^2 & K_{22}^2 \end{array}\right]\left[\begin{array}{l} U_1 \\ U_2 \\ U_3 \end{array}\right]=} \\ {\left[\begin{array}{c} F_1-K_{12}^1 \Delta U_2^1 \\ F_2-K_{22}^1 \Delta U_2^1-K_{11}^2 \Delta U_1^2 \\ F_3-K_{21}^2 \Delta U_1^2 \end{array}\right] .} \end{array}$ | (7) |
由此可以看出,在分裂节点法中,断层位错的引入体现在单元、总体的载荷向量上,而对于单元、总体的刚度矩阵是没有影响的,大大简化了刚度矩阵和载荷向量的组装,且对于计算的准确性和稳定性没有影响[19],体现了该方法的简洁性和有效性。
1.2 有限元与理论解结果对比为验证我们自主研发的采用分裂节点技术的三维并行弹性有限元程序的有效性,我们建立了一个三维走滑断层地震模型(模型1)和一个三维逆断层地震模型(模型2),分别利用有限元程序和基于半无限空间位错理论[23]的Coulomb 3.3[17-18]及edgrn/edcmp[21]计算2个断层模型的地表同震位移场,并对比两者的结果。2个断层模型的参数如表 1所示。
|
|
表 1 走滑和逆冲断层地震模型的材料参数与断层参数 Table 1 The material parameters and fault parameters of strike-slip and reverse fault earthquakes |
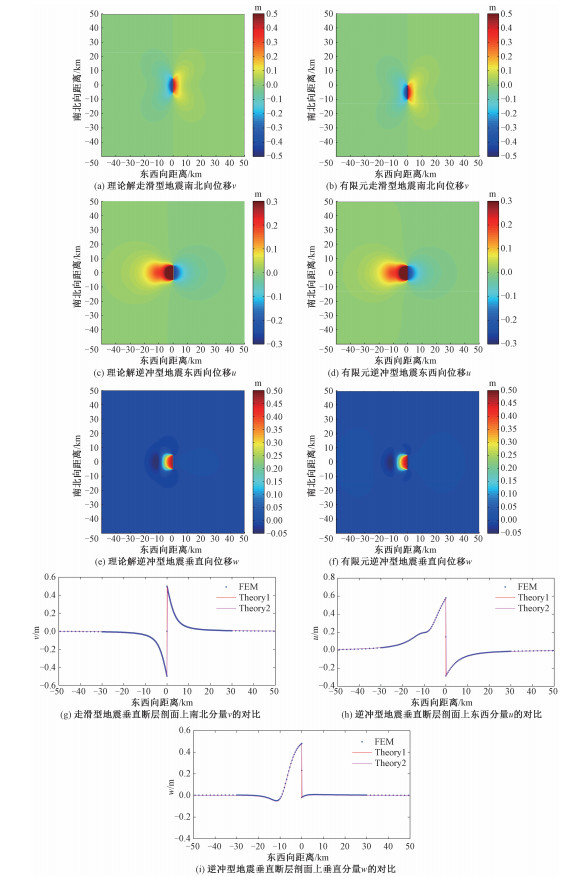
图 3分别展示了理论解和有限元计算得到的走滑断层和逆断层的同震地表位移的等值线图和剖面结果图。图 3(a)~3(f)左侧为Coulomb3.3[17-18]解析解结果,右侧为有限元模拟结果,表明有限元得到的走滑断层地震和逆断层地震引起的地表同震位移的分布形态与理论解有很好的一致性。图 3(g)~3(i)分别给出了有限元和理论解的过断层中心点垂直断层走向的剖面上走滑断层地震的南北向同震位移、逆断层地震的东西向位移和垂直向位移的对比图,FEM表示有限元模拟结果,Theory1表示Coulomb3.3[17-18]计算结果,Theory2表示edgrn/edcmp[21]计算结果,表明有限元与理论解有很好的一致性。
|
Download:
|
| 图 3 走滑断层和逆断层地震引起的同震位移的有限元模拟结果与解析解对比 Fig. 3 Comparison of the analytical solutions with finite element models simulation results for the coseismic displacement components of the strike-slip fault and thrust fault | |
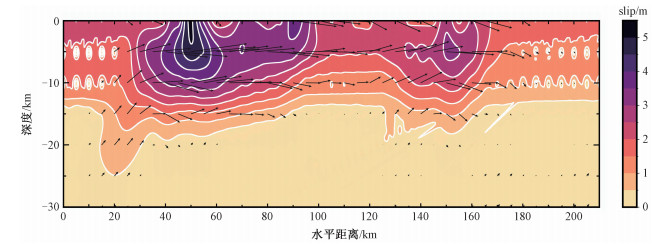
采用前人反演得到的非均匀位错模型以及我们基于分裂节点技术[22]的有限元方法,本文计算了玛多地震的同震位移和同震应力场。有限元模型东西长1 100 km,南北长1 000 km,深度100 km,共有64个并行计算分区,有限元网格数量为2 171 715,可以实现较高分辨率的有限元并行计算。本文采用中国地震局地质研究所的非均匀位错有限断层模型[15],如图 4所示。
本文建立了2个有限元模型:均匀模型和分层模型,其材料参数如表 2所示,杨氏模量和泊松比可由表中的密度、P波速度和S波速度计算得到。由于有限元模型的尺寸大大超过主震断层,本文假定除模型上表面(地表)外,其余边界上的法向位移为0。
|
|
表 2 玛多地震同震变形三维有限元分层模型的材料参数(自USGS) Table 2 Material parameters of the 3D finite element layered model of Maduo earthquake(USGS) |
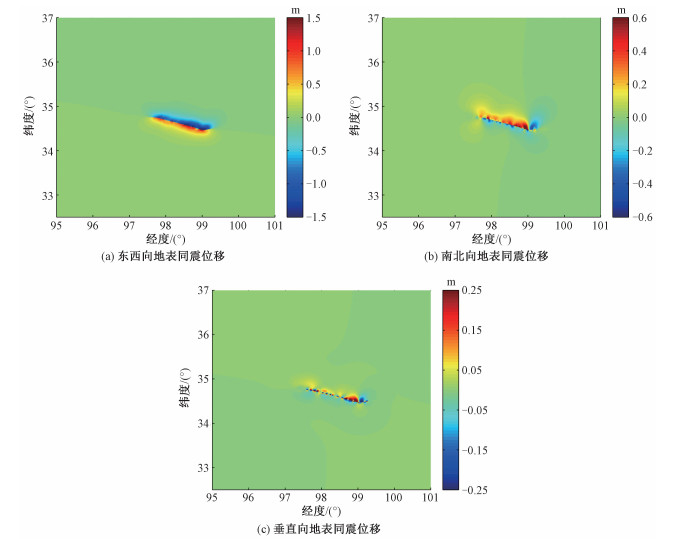
根据上述三维弹性有限元模型,本文模拟得到的玛多地震地表同震位移场见图 5。东西向位移u大于零的部分位于断层南侧,小于零的部分主要集中于断层北侧,说明断层南侧以向东运动为主,断层北侧则以向西运动为主(图 5(a));南北向位移v大于零的部分位于断层北侧,小于零的部分主要集中于断层东南部,说明断层南侧以向南运动为主,断层北侧以向北运动为主,呈现拉张的运动方式(图 5(b))。以上同震位移场分布特征与玛多地震具有明显的左旋走滑机制一致;垂向位移w大于零的部分位于断层北部,小于零的部分位于断层南部,断层北部为上升盘,南部为下降盘,上升盘为断层下盘,下降盘为上盘(图 5(c)),表明发震断层具有正断分量。
|
Download:
|
| 图 5 玛多地震的地表同震位移分量等值线图 Fig. 5 Contour maps of surface coseismic displacement components of Maduo earthquake | |
本文计算结果中玛多地震引起的研究区域内主要断层10 km深度的应力变化,如图 6所示。图中正应力变化大于零的区域表示拉应力增加,主要位于断层南西侧和北东侧,与拉应力减小的区域交错分布(图 6(a));剪应力变化在发震断层两侧是小于零的,在断层尖端向外是大于零的(图 6(b));库仑应力变化在断层两侧基本上是小于零的,库仑应力变化大于零的区域以断层两端为中心(图 6(c)和6(d)中的白色曲线分别是库仑应力变化的0和0.001 MPa的等值线),在断层两侧呈蝴蝶状对称分布(图 6(c)、6(d))。9~11 km深度范围内除主震断层带两侧大于1.0级的余震基本位于10 km深度水平面上平行于主震的库仑应力变化大于零的区域(图 6(d))。

|
Download:
|
| 黑色空心圆圈表示9~11 km深度的M≥1.0的地震。 图 6 玛多地震引起的深度为10 km水平面与主震震源机制一致的微元面上的同震应力变化 Fig. 6 The coseismic stress changes on the plane consistent with the focal mechanism of the main earthquake of Maduo earthquake at 10 km depth | |
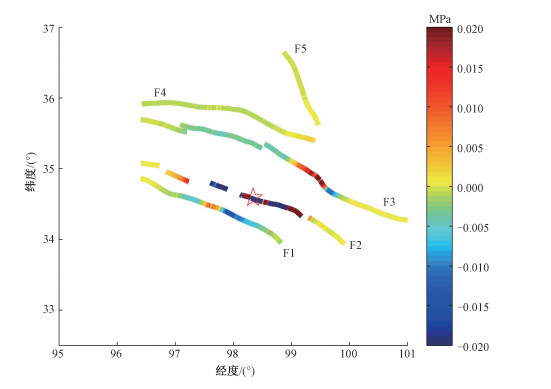
本文同时计算了研究区域内与玛多地震发震断层相邻的5条断层上的同震库仑应力变化,如图 7,计算使用的有效摩擦系数为0.4[24]。结果表明,玛多地震引起鄂拉山断裂南段、昆中断裂东段、东昆仑断裂带的大部分(除中部靠西的小部分外)、玛多—甘德断裂北西段、南东段及主震震中附近以及达日断裂带北西段库仑应力增加,地震危险性增加,这些地方是需要密切关注、加强地震监测的区域。
|
Download:
|
|
F1:达日断裂带;F2:玛多—甘德断裂带;F3:东昆仑断裂带;F4:昆中断裂带;F5:鄂拉山断裂带,断层数据引自詹艳等[4]。 五角星为2021年5月22日青海玛多MS7.4地震的震中。 图 7 玛多地震震中周围主要断裂上的库仑应力变化 Fig. 7 Coulomb stress change on the major faults around the epicenter of Maduo earthquake |
|
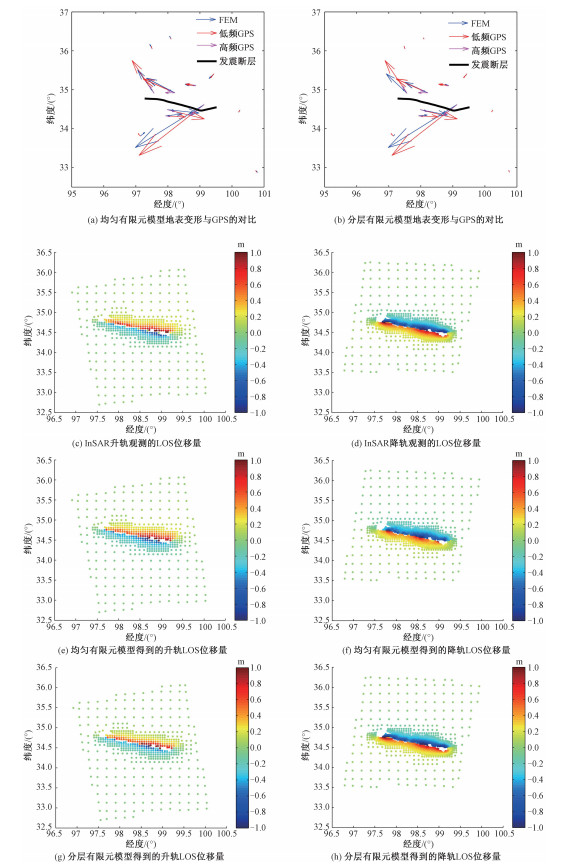
为验证本文采用分裂节点有限元方法模拟实际大地震同震变形的有效性,本文设计了玛多地震的2种不同介质模型:均匀介质模型和分层介质模型,2种模型材料参数如表 2。本文分别计算了2种介质模型的同震变形场,并将其处理为卫星视线方向LOS位移量,与GPS观测的同震水平位移、InSAR升降轨LOS位移量观测结果进行对比,结果如图 8所示。图 8(a)、8(b)中的黑线表示玛多地震发震断层,蓝线表示有限元模型模拟结果,红线表示GPS观测结果(低频),粉线表示GPS观测结果(高频),左侧是均匀有限元模型模拟结果,右侧是分层有限元模型模拟结果。图 8(c)、8(e)、8(g)分别是InSAR升轨的观测数据、均匀和分层有限元模型模拟结果。图 8(d)、8(f)、8(h)分别是InSAR降轨的观测数据、均匀和分层有限元模型模拟结果,表明均匀有限元和分层有限元模型得到的升轨和降轨的卫星视线方向LOS位移量与InSAR观测得到的卫星视线方向LOS位移量有较好的一致性。
|
Download:
|
| 图 8 玛多地震同震变形有限元模拟结果与GPS及InSAR观测结果对比图 Fig. 8 Comparison of the finite element models simulation results with GPS and InSAR observations for the coseismic deformations of Maduo earthquake | |
本文采用统计均方根(root mean square, RMS)方法对有限元模拟结果和观测变形量之间的差异进行定量说明。RMS[15]定义如下
| $\overset\frown{\sigma }=\sqrt{\sum\limits_{i=1}^n\left(u_{\mathrm{obs}}^i-u_{\mathrm{cal}}^i\right)^2 / n} .$ | (8) |
uobsi表示同震位移的GPS和InSAR观测数据;ucali表示同震位移的有限元模拟结果;n表示观测数据的数量。玛多地震同震位移的有限元模拟结果与观测位移量之间的RMS如表 3所示。
|
|
表 3 玛多地震同震位移的有限元模拟结果与大地测量观测位移量之间的RMS Table 3 RMS comparison of finite element simulation results and geodetic observed coseismic displacement of Maduo earthquake |
从表 3可以看出,有限元模拟同震位移的结果与大地测量观测结果之间的RMS在合理范围之内,与杨君妍等[15]的计算结果一致,说明本文所采用的有限元方法对大地震同震变形的模拟是有效的。
本文通过分裂节点法将位错数据加入有限元模型计算的同震位移结果表明,发震断层南侧以向东、向南及向下运动为主,断层北侧则以向西、向北及向上运动为主,总体表现为有正断分量的左旋走滑断层。该计算结果与杨君妍等[15]使用球形分层地球模型位错理论、谈洪波等[19]使用均匀半空间位错理论进行同震位错计算的解析法或半解析法所得结果基本一致。
3.2 玛多地震对巴颜喀拉地块及周边地震危险性的影响本文玛多地震同震库仑应力计算结果表明,发震断层的两侧沿走向方向上库仑应力下降,而在断层两端及以两端为中心呈蝴蝶状发散的区域内,库仑应力增加。这个现象表明玛多地震对发震断层及断层周边地壳产生了显著的应力调整:玛多地震部分释放了发震断层所积累的应力(发震断层两侧的库仑应力变化大部分都是显著降低),也造成断层两端及周边部分区域的地壳应力积累(图 6(c))。该结果与杨光远等[16]利用Coulomb 3.3程序在同等条件(10 km深度处和主震震源机制一致的微元面)下的计算结果对比,同震库仑应力分布基本一致。我们的模拟结果还表明,9~11 km深度范围内除主震断层带两侧大于1.0级的余震基本位于10 km深度水平面上平行于主震的库仑应力变化大于零的区域(图 6(d))。研究区域内鄂拉山断裂、昆中断裂、东昆仑断裂、玛多—甘德断裂以及达日断裂这5条主要断裂的同震库仑应力结果表明: 玛多地震引起鄂拉山断裂南段,昆中断裂东段,东昆仑断裂带的大部分、玛多—甘德断裂西北段和东南段以及达日断裂带北西段库仑应力增加(图 7)。鄂拉山断裂南段与昆中断裂东段位于巴颜喀拉块体北部的东昆仑—柴达木块体,历史上该地区曾发生过M5~M6及M6~M7地震,此次玛多地震引起该地区库仑应力增加,具有较高的地震危险性,应对其密切关注。东昆仑断裂带历史上曾发生过如1937年MS7.5地震(阿拉克湖—托索湖段和下大武段)、1963年MS7.0地震(秀沟—阿拉克湖段)以及2001年MS7.1地震(库赛湖段),是一条活跃断裂带[25]。玛多地震使玛沁—玛曲段东南段和托索湖—下大武段东南段库仑应力增加,这与Li等[20]的结果一致。这2个断裂段在玛多地震时产生应力积累,加之玛沁—玛曲段近年来未发生大地震,导致该地区地震危险性大大增加,应当加强地震监测、做好防震防灾工作。玛多—甘德断裂中段库仑应力变化分布较为复杂,库仑应力显著增加与显著降低的区段交错分布,可能与其复杂的断层结构有关[4]。玛多—甘德断裂部分区段库仑应力显著降低可能与玛多地震释放了其部分应力有关,但其两端的库仑应力显著增加,地震危险性有所提高。位于玛多地震发震断层南部的达日断裂带北段及中段库仑应力增加,而其余部分库仑应力水平下降,考虑到1947年达日M7.7地震所带来的达日断裂带西北段库仑应力增加及其较高的应力积累速率[26],其地震危险性仍需进一步研究与评估。
4 结论本文采用分裂节点技术开发三维并行弹性有限元程序,并通过地震位错模型的理论解验证了有限元程序的正确性。该有限元程序能够考虑复杂几何、非均匀材料和位错非均匀分布,可以模拟计算大地震同震变形。利用该程序模拟计算了玛多MS7.4地震的同震位移场、应力场及库仑应力变化,计算得到的地表同震位移结果与GPS和InSAR大地测量数据一致。模拟结果确认了玛多MS7.4地震的发震断层为一条左旋走滑兼有正断分量的断层。计算得到的库仑应力增加的区域与玛多地震的余震分布有较好的对应性。库仑应力结果表明,玛多地震引起了鄂拉山断裂南段,昆中断裂东段,东昆仑断裂带的大部分区段、玛多—甘德断裂西北段和东南段以及达日断裂带北西段库仑应力增加,这些区域的地震危险性增加,是未来需重点关注的地区。
石耀霖院士和周永发博士对本研究自主研发的三维有限元程序编制给予了很多建设性的指导和帮助,周元泽教授对论文初稿提出了很多建设性的意见,在此一并表示感谢。
| [1] |
邓文泽, 杨志高, 席楠, 等. 2021年5月22日青海玛多M7.4地震的快速测定与数据产品产出[J]. 中国地震, 2021, 37(2): 541-550. Doi:10.3969/j.issn.1001-4683.2021.02.025 |
| [2] |
王未来, 房立华, 吴建平, 等. 2021年青海玛多MS7.4地震序列精定位研究[J]. 中国科学: 地球科学, 2021, 51(7): 1193-1202. Doi:10.1360/SSTe-2021-0149 |
| [3] |
徐志国, 梁姗姗, 张广伟, 等. 2021年5月22日青海玛多MS7.4地震发震构造分析[J]. 地球物理学报, 2021, 64(8): 2657-2670. Doi:10.6038/cjg2021P0390 |
| [4] |
詹艳, 梁明剑, 孙翔宇, 等. 2021年5月22日青海玛多MS7.4地震深部环境及发震构造模式[J]. 地球物理学报, 2021, 64(7): 2232-2252. Doi:10.6038/cjg2021O0521 |
| [5] |
李志才, 丁开华, 张鹏, 等. GNSS观测的2021年青海玛多地震(MW 7.4)同震形变及其滑动分布[J]. 武汉大学学报·信息科学版, 2021, 46(10): 1489-1497. Doi:10.13203/j.whugis20210301 |
| [6] |
尹欣欣, 王维欢, 蔡润, 等. 2021年青海玛多MS7.4地震精定位和发震构造初探[J]. 地震工程学报, 2021, 43(4): 834-839. Doi:10.3969/j.issn.1000-0844.2021.04.834 |
| [7] |
潘家伟, 白明坤, 李超, 等. 2021年5月22日青海玛多MS7.4地震地表破裂带及发震构造[J]. 地质学报, 2021, 95(6): 1655-1670. Doi:10.19762/j.cnki.dizhixuebao.2021166 |
| [8] |
李智敏, 李文巧, 李涛, 等. 2021年5月22日青海玛多MS7.4地震的发震构造和地表破裂初步调查[J]. 地震地质, 2021, 43(3): 722-737. Doi:10.3969/j.issn.0253-4967.2021.03.016 |
| [9] |
周保, 李五福, 董福辰, 等. 青海省玛多县"5.22 MS7.4地震"地表破裂与次生灾害发育特征[J/OL]. 地质通报, (2021-07-27)[2021-08-12]. https://kns.cnki.net/kcms/detail/11.4648.P.20210726.1650.002.html.
|
| [10] |
盖海龙, 姚生海, 杨丽萍, 等. 青海玛多"5·22" MS7.4级地震的同震地表破裂特征、成因及意义[J]. 地质力学学报, 2021, 27(6): 899-912. Doi:10.12090/j.issn.1006-6616.2021.27.06.073 |
| [11] |
华俊, 赵德政, 单新建, 等. 2021年青海玛多MW7.3地震InSAR的同震形变场、断层滑动分布及其对周边区域的应力扰动[J]. 地震地质, 2021, 43(3): 677-691. Doi:10.3969/j.issn.0253-4967.2021.03.013 |
| [12] |
Liu J H, Hu J, Li Z W, et al. Complete three-dimensional coseismic displacements due to the 2021 Maduo earthquake in Qinghai Province, China from Sentinel-1 and ALOS-2 SAR images[J]. Science China Earth Sciences, 65. Doi:10.1007/s11430-021-9868-9 |
| [13] |
Liu C Y, Bai L, Hong S Y, et al. Coseismic deformation of the 2021 MW7.4 Maduo earthquake from joint inversion of InSAR, GPS, and teleseismic data[J]. Earthquake Science, 2021, 34(5): 1-11. Doi:10.29382/eqs-2021-0050 |
| [14] |
Zhao D Z, Qu C Y, Chen H, et al. Tectonic and geometric control on fault kinematics of the 2021 MW7.3 Maduo (China) earthquake inferred from interseismic, coseismic, and postseismic InSAR observations[J]. Geophysical Research Letters, 2021, 48(18): e2021GL095417. Doi:10.1029/2021GL095417 |
| [15] |
杨君妍, 孙文科, 洪顺英, 等. 2021年青海玛多7.4级地震的同震变形分析[J]. 地球物理学报, 2021, 64(8): 2671-2683. Doi:10.6038/cjg2021P0416 |
| [16] |
杨光远, 李一帆, 王斌, 等. 青海玛多7.4级地震静态库仑应力分析[J]. 四川地震, 2021, 3: 1-4. Doi:10.13716/j.cnki.1001-8115.2021.03.001 |
| [17] |
Toda S, Stein R S, Richards-Dinger K, et al. Forecasting the evolution of seismicity in southern California: animations built on earthquake stress transfer[J]. Journal of Geophysical Research: Solid Earth, 2005, 110(B5): B05S16. Doi:10.1029/2004JB003415 |
| [18] |
Lin J, Stein R S. Stress triggering in thrust and subduction earthquakes and stress interaction between the southern San Andreas and nearby thrust and strike-slip faults[J]. Journal of Geophysical Research: Solid Earth, 2004, 109(B2): B02303. Doi:10.1029/2003JB002607 |
| [19] |
谈洪波, 王嘉沛, 杨光亮, 等. 2021年玛多MS7.4地震的震后效应模拟[J]. 地震地质, 2021, 43(4): 936-957. Doi:10.3969/j.issn.0253-4967.2021.04.013 |
| [20] |
Li Y J, Huang L Y, Ding R, et al. Coulomb stress changes associated with the M7.3 Maduo earthquake and implications for seismic hazards[J]. Natural Hazards Research, 2021, 1(2): 95-101. Doi:10.1016/j.nhres.2021.06.003 |
| [21] |
Wang R J, Martín F L, Roth F. Computation of deformation induced by earthquakes in a multi-layered elastic crust: FORTRAN programs EDGRN/EDCMP[J]. Computers & Geosciences, 2003, 29(2): 195-207. Doi:10.1016/S0098-3004(02)00111-5 |
| [22] |
Melosh H J, Raefsky A. A simple and efficient method for introducing faults into finite element computations[J]. Bulletin of the Seismological Society of America, 1981, 71(5): 1391-1400. Doi:10.1785/bssa0710051391 |
| [23] |
Okada Y. Internal deformation due to shear and tensile faults in a half-space[J]. Bulletin of the Seismological Society of America, 1992, 82(2): 1018-1040. Doi:10.1785/bssa0820021018 |
| [24] |
King G C P, Stein R S, Lin J. Static stress changes and the triggering of earthquakes[J]. Bulletin of the Seismological Society of America, 1994, 84(3): 935-953. Doi:10.1785/bssa0840030935 |
| [25] |
邓起东, 高翔, 陈桂华, 等. 青藏高原昆仑—汶川地震系列与巴颜喀喇断块的最新活动[J]. 地学前缘, 2010, 17(5): 163-178. |
| [26] |
刘雷, 李玉江, 朱良玉, 等. 1947年达日M7.7地震对巴颜喀拉块体边界断裂应力影响的数值模拟[J]. 地球物理学报, 2021, 64(7): 2221-2231. Doi:10.6038/cjg2021P0194 |
 2024, Vol. 41
2024, Vol. 41