2. 中国科学院信息工程研究所信息安全国家重点实验室, 北京 100093
2. State Key Laboratory of Information Security, Institute of Information Engineering, Chinese Academy of Sciences, Beijing 100093, China
随着信息技术的快速发展,密码应用日益受到关注。RNG作为密码算法、密码协议等众多密码技术的安全基石,其输出被称为随机数。随机数被广泛地用于对称或非对称密码算法的密钥产生、挑战-响应方案中的挑战值、数字签名方案中的秘密信息,以及抗侧信道分析攻击等密码应用中。按随机性来源和生成原理的不同,RNG主要分为真随机数发生器(true RNG, TRNG)和伪随机数发生器(pseudo RNG, PRNG)[1]。TRNG是采集某些物理现象(如电路噪声、核裂变)中的随机成分,经数字化处理后生成随机数。PRNG则是采用确定性算法(如LFSR[2]、冯.诺依曼后处理[3])将一段有限长的随机序列(也称为种子,通常由TRNG生成)扩展成任意长度的输出序列。
TRNG又可细分为基于物理源的硬件RNG(hardware RNG, HRNG)和基于外部非物理源的软件RNG(software RNG, SRNG)[4]。HRNG生成的数据通常具有良好的不可预测性,但随着便携式物联网、智能移动终端等设备的不断普及,传统的HRNG存在硬件更新困难、开发成本高等问题,导致适用范围受限,仅部分平台可以调用HRNG接口[5]。此外,如果HRNG的器件出现老化或存在偏差等问题,也很难修复[6]。
目前,已有诸多系统平台使用SRNG提供随机数服务,如Linux随机数发生器(即LRNG)[7]、基于LRNG实现的Android系统的随机数发生器(APRNG)[8]、iOS系统使用的Yarrow[9]、基于Yarrow设计的Fortuna随机数发生器[10],以及Windows内核的随机数发生器CryptGenRandom[11]。由于SRNG中的熵源不可控,对后处理算法设计和实现的安全性要求较高,因此出现了许多针对SRNG设计实现的分析和攻击。相关工作主要集中在熵源数据的安全性和后处理模块内部状态的安全性方面。在熵源数据安全性方面,攻击者通过一些攻击手段可以影响熵源数据的安全性,如return-to-libc攻击[12]、return-oriented攻击[13]等缓冲区溢出攻击,通过构造函数并调用参数将原地址重定位到攻击者的地址;熵源数据熵可能达不到预期需求,造成SRNG内部状态泄漏、输出数据可预测等安全风险,如OpenSSL的RNG中,Strenzke[8]指出若输入数据熵不足,即使后续RAND add()函数会输入新数据来增加熵,但仍存在RNG输出数据存在低熵的隐患。在后处理模块内部状态的安全性方面,攻击者利用Dual EC算法存在的参数后门[14-16]来泄露RNG的内部状态,破坏RNG输出序列的不可预测性。
综合上述研究,我们发现,为提升SRNG设计和使用时的安全性,应重点考虑以下两个方面:1)多种攻击手段会影响熵源数据的安全,不安全的熵源数据会导致SRNG提供的随机数服务存在严重安全隐患。因此,在SRNG实际运行时,对未处理序列的熵值(熵源数据的质量)进行在线监控是必要的,并可在熵不足的情况下调用后处理模块改善输出序列的统计特性;2)如何设计实现具有高安全性的SRNG后处理扩展算法,以确保后处理模块中内部状态以及输出序列的安全性。基于上述考虑,本文设计并实现了一种带有熵监控功能的软件随机数发生器(entropy monitoring SRNG, EM-SRNG)。
本文的主要贡献如下:
1) 选取高精度时间序列作为熵源数据。由于读取高精度系统时间的指令在取值、译码和执行3个阶段存在不确定性的时间误差。EM-SRNG将纳秒时间的末位数据作为架构中的未处理序列,其具有良好的不可预测、数据产生速率高等特点。虽然许多相关研究已将时间序列作为随机源,但存在由于熵源事件频繁发生而导致时间数据重复率和连续性较高的缺点,以LRNG为例,后续需要额外操作消除熵池数据之间的相关性。
2) 提出一种基于NIST SP 800-90B测试套件的实时在线熵监控机制,实时监测EM-SRNG运行时熵源数据的质量,能够基于熵量化未处理序列的质量,在设定熵阈值的情况下,对熵不足的未处理序列,能够智能选择调用后处理模块,避免冗余的计算资源开销。
3) 实现高安全性的后处理模块,以确保EM-SRNG后处理模块中内部状态的安全性。EM-SRNG的后处理模块基于中国自主研制的SM系列密码算法设计而成,可选用基于SM3和SM4密码算法设计的两种后处理扩展算法,用于提高内部状态的安全性以及改善输出序列的统计特性。
1 相关工作本章首先介绍SRNG的基本模型,简要阐述SRNG结构中各组成部分的功能。其次,介绍操作系统平台SRNG的典型设计,包括LRNG、ARNG、iOS系统的Yarrow和基于Yarrow设计的Fortuna随机数发生器,以及Windows内核的RNG。最后,介绍SRNG的安全性评估要求和评估方法。
1.1 SRNG模型本文在参考德国BSI的AIS 20/31[17]和ISO/IEC 18031[4]的基础上,梳理出SRNG的基本模型。SRNG模型主要包含熵源、初始化函数、内部状态、种子更新函数和输出函数,其随机数生成基本原理如下:将熵源事件数字化后的未处理序列作为SRNG的输入,首先将未处理序列输入初始化函数,并开始内部状态迭代,然后通过输出函数对内部状态进行更新,最后产生外部请求的随机数。种子更新函数是利用熵源数据更新内部状态,通过条件控制(如输出数据长度达到上限)执行种子更新操作。
1.2 基于操作系统平台的典型SRNG设计软件随机数发生器目前已有许多成熟的设计方案,按照操作系统平台划分,有Mac、Linux、Android和Windows内核所带的随机数发生器。
iOS和Mac OS X操作系统,使用由Kelsey等[9]设计完成的Yarrow发生器。Yarrow发生器内部包含快熵池和慢熵池,通过统计熵池中同种熵源事件类型的熵值,进而确定是否执行更新内部状态(重播种)操作。该发生器使用3种不同的熵估计方法计算不同熵源事件的熵值,并取3种熵估计方法中的最小值作为熵源的最终熵值。最后,通过基于计数器工作模式的分组算法作为后处理算法来产生随机数。由于Yarrow输出序列的质量在很大程度上依赖于熵估计方法的准确性,为此Viega[10]在Yarrow的基础上,选择去掉熵估计环节,通过多熵池保证至少有一个熵池积累足够的熵来提供安全性,据此提出Fortuna随机数发生器。Fortuna通过32个多熵池和新重播种策略更新RNG内部状态。最后通过基于计数器工作模式的分组算法生成随机数。
Android操作系统上,APRNG的熵源数据主要来源于Linux内核提供的随机数。APRNG主要使用OpenSSL密码库中随机数发生器的3个应用程序函数接口:RAND_poll()是初始化内部状态接口,RAND_add()是数据输入接口,RAND_byte()是随机数输出接口。Windows操作系统上,Dorrendorf等[12]分析Windows内核的随机数发生器CryptGenRandom的结构,其使用RC4对称加密算法更新内部状态。
Linux操作系统上,LRNG是目前应用最广泛的RNG。LRNG包含主熵池、阻塞熵池和非阻塞熵池,每个熵池都含有熵值计数器,用来统计对应熵池中数据的熵值。LRNG从外界收集4种熵源事件,包括鼠标移动、敲击键盘、中断和磁盘输入输出操作,并将熵源事件类型编码和事件发生时间添入熵池。
LRNG熵估计方法被称为“三阶时间差”方法,通过计算熵源事件发生的时间差估计熵值,计算方法具体如下:
1) 计算时间差:
| $ \begin{array}{l} {\lambda _i} = {t_i} - {t_{i - 1}}, \\ \lambda _i^2 = {\lambda _i} - {\lambda _{i - 1}}, \\ \lambda _i^3 = \lambda _i^2 - \lambda _{i - 1}^2. \end{array} $ | (1) |
其中,ti表示熵源事件i发生的的时间。
2) 选择最小差:
| $ \Delta i = \min \left( {\left| {{\lambda _i}} \right|, \left| {\lambda _i^2} \right|, \left| {\lambda _i^3} \right|} \right). $ | (2) |
3) 计算熵值:
| $ Ei = \log 2\Delta i. $ | (3) |
此外,LRNG提供两种接口获取随机数,一种内核层输出接口get_random_bytes,另一种是用户层/dev/random或者/dev/urandom文件接口。/dev/random从阻塞熵池提取随机数,阻塞熵池每次在输出随机数之前,会先判断熵值计数器值是否达到设定的阈值,进而判断是否输出随机数。/dev/urandom是从非阻塞熵池提取随机数,若非阻塞熵池不空,则/dev/urandom接口可持续输出随机数。
1.3 安全性评估对于SRNG,要求其能够抵抗内部或者外部的攻击。对于以软件形式实现的随机数发生器,攻击者被假定已知随机数发生器的设计目标和算法实现,并且通过一些攻击手段,可以获取发生器某一时刻的内部状态的相关信息。因此,SRNG在设计和使用时,应保证满足以下安全要求[18]:
1) 伪随机性(R1):SRNG输出的随机数对外部观察者来说应该是随机的。采用密码算法对原始数据进行混淆和扩散,可以满足此安全要求。
2) 前向安全性(R2):对于一个攻击者而言,即便他获取了发生器在某一特定时刻的状态,也不能获知在此之前任意时刻的输出。目前,使用单向函数(如散列函数)可满足R2要求。
3) 后向安全性(R3):对于一个攻击者而言,即便他获取了发生器在某一特定时刻的状态,也不能获知在此之后任意时刻的输出。Barak和Halevi[18]对SRNG的后向安全性进行分析,指出在输出函数是确定性算法的情况下,在用户每次请求随机数之间更新内部状态,可以实现保证后向安全性的目的。
为保证SRNG满足以上安全性要求,提供高质量的随机数服务,SRNG的安全性检测是必不可少的。目前,常用的RNG安全性评估方法包括:黑盒统计检测、理论熵估计和统计熵估计。
黑盒统计检测是传统的随机性检测手段。由于早期熵评估的困难,人们一直在采用后验检测的方法对输出序列进行检测来判定随机数发生器的随机性。所谓随机性的后验检测,就是先假设熵是满的(完全真随机),则输出序列应该满足多种统计分布,通过检测输出序列是否满足这些统计分布判断序列是否完全真随机。目前有很多统计测试套件被广泛认可和使用,如NIST发布的SP 800-22[19]、TestU01[20]、佛罗里达州立大学Marsaglia开发的Diehard测试[21]和《GB/T 32915—2016信息安全技术二元序列随机性检测方法》[22](中国的随机性统计检测标准)。由于黑盒统计测试并不关注随机数生成原理和发生器内部结构,而是只检测输出序列的质量,因此具有很好的通用性和可操作性。
理论熵估计是在完全了解随机数发生器内部结构和产生原理的情况下,通过建立数学模型的方法对输出序列的熵进行理论计算。这种测试方法一般用于对硬件随机数发生器的理论安全性进行证明。
统计熵估计是介于理论熵估计和黑盒统计检测二者之间的RNG安全测评方法。一方面,该方法继续沿用当前最受推崇的随机数检测方式——“熵评估”来指导检测技术的设计与实施;另一方面,该方法采用黑盒统计检测的工作模式,使得其对任何结构和产生原理的发生器都具有较好的通用性。目前,这类测试方法中的典型是NIST SP 800-90B(简称“90B”)[23]。
2 带有熵监控功能的SRNG架构 2.1 安全假设本文假设攻击者无法破坏Linux内核的安全性,并且不考虑侧信道攻击。Linux内核的安全体现在对代码段和数据段的保护。目前,已有方案可以对Linux内核的代码段和数据段进行保护,如集成OSck[24],一个能够检测内核rootkit是否对操作系统数据存在恶意修改的系统;或者使用KI-MON[25],基于硬件事件触发的内核完整监控平台;它们可以保护内核数据段,保证内核数据的正确性。TF-BIV[26]依赖散列值对二进制文件的完整性进行校验,在保证散列函数是安全的前提下,可以对内核静态代码进行完整性保护。本文EM-SRNG的熵源事件发生于Linux内核中,Linux内核的安全性可以保证数据源产生的安全性。
2.2 EM-SRNG设计我们设计了一种带有熵监控功能的软件随机数发生器(EM-SRNG),架构如图 1所示,包含熵源、熵监控和后处理3个模块,其中熵监控模块可分为熵估计和熵判断两个环节,熵判断的结果决定主熵池数据是否进入后处理模块进行处理。下面详细阐述EM-SRNG输出随机数的步骤:

|
Download:
|
| 图 1 EM-SRNG架构 Fig. 1 EM-SRNG architecture | |
1)“纳秒级”时间熵源采集:以操作系统平台“纳秒级”时间数据作为熵源进行采集和数字化处理。由于读取高精度系统时间的指令在取指、译码和执行阶段存在不确定性的时间误差,使得纳秒时间数据具有良好的随机性。纳秒时间数据的不确定性可以作为EM-SRNG随机性的来源。EM-SRNG熵源模块设计原理见2.2.1小节。
2) 熵估计熵池数据:对主熵池数据所含信息量进行估计。EM-SRNG在线熵估计环节基于NIST SP 800-90B统计测试套件实现,可实时计算主熵池数据的保守熵估计,即在最差情况下主熵池数据所含熵值,从而避免高估熵值带来的危害。EM-SRNG熵估计环节设计原理见2.2.2小节。
3) 熵判断和后处理:熵判断模块会将来自于熵估计器的测量值和预设的熵阈值相比较,根据测量值和阈值的大小关系,判断未处理序列是否需要进入后处理模块(对应不同的熵池,熵池1的数据无需进入后处理模块;熵池2的数据需要进入后处理模块处理)以改善输出序列的统计特性,从而有效降低了由于调用后处理模块而造成的资源开销,同时保证了EM-SRNG的输出质量。后处理模块基于中国商用密码算法设计而成,分别应用SM3杂凑算法和SM4分组算法,具有高可靠性、提供前向安全性和后向安全性等特点。SM3杂凑算法和SM4分组算法是中国典型的商用密码算法,同时SM3算法又是ISO/IEC国际标准,SM3和SM4算法可用于后处理模块设计方案中。EM-SRNG后处理模块设计原理见2.2.3小节。
EM-SRNG提供bool random_srng(int length, char* random_buffer)函数接口生成应用程序请求的length长度的随机数,随机数存储于缓冲区random_buffer中,返回给应用程序。返回值是布尔类型,若返回true,代表输出序列是经EM-SRNG后处理模块计算得到的数据;否则,输出序列未经EM-SRNG后处理模块的处理。EM-SRNG的后处理模块可选用基于SM3杂凑算法和SM4分组算法的两种后处理扩展算法,开发人员可自主选择使用何种后处理扩展算法。
2.2.1 熵源EM-SRNG熵源来自Linux高精度纳秒级时间。在Linux操作系统用户空间下,读取系统时间主要通过读内核中xtime全局变量。xtime从CMOS电路中获取系统时间,是 < linux/time.h>文件中timespec结构体变量,精确度是ns。
由于受CPU型号、温度和电压等物理因素以及CPU指令中断、进程调度、乱序执行和指令预测的影响,指令在取指、译码和执行3个阶段都存在不确定性的时间误差,时间误差在纳秒级。所以软件读取高精度系统时间存在随机偏差,使得其无法被敌手或用户影响。因此,在EM-SRNG设计方案中,我们选取纳秒级时间序列作为熵源数据。此外,熵源数据的产生速率也是SRNG设计方案中关注的一大方面,SRNG要求熵源数据采集过程简单。目前,Linux操作系统已为用户空间提供了读取系统时间的函数接口,其读取系统时间数据的速率较快。
2.2.2 熵监控熵监控功能由两个独立的环节协同完成,即熵估计环节和熵判断环节。EM-SRNG的熵估计环节基于NIST SP 800-90B测试包设计而成,用于在发生器运行时对主熵池中数据的在线熵检测,实时监测未处理序列熵值的变化。
本方案选用NIST SP 800-90B测试包设计发生器中在线熵估计器,这种基于最小熵的统计测试方法有3点好处:1)最小熵是一种保守的熵估计方法,适用于评价面向较高安全需求的随机数服务,例如在操作系统环境下,经常使用操作系统的随机数发生器产生的数据作为确定性随机数发生器的种子;2)由于非物理熵源的行为特征难以用特定概率分布刻画,因此很难采用理论建模方式量化SRNG的熵值;3)统计熵评估方法既从熵的角度评价SRNG质量,又可以用编程语言快速实现,且执行效率高,对计算资源消耗低。
熵判断是根据熵池中数据的熵值与阈值的关系来进行不同通路的选择。熵判断是为了确保EM-SRNG的输出质量,在熵源数据达不到要求质量的前提下,对熵源数据经过后处理模块混淆。而在熵源数据达到要求质量的情形下,直接输出随机数,减少密码计算对资源的浪费,提高EM-SRNG整体性能。而在LRNG设计方案中,无论熵池数据的质量如何,从熵池输出时,数据都将经过确定性密码算法处理后才能作为随机数,这种做法很容易造成冗余的资源开销。
2.2.3 后处理模块EM-SRNG的后处理模块包含两种后处理扩展算法,分别基于SM3和SM4密码算法进行设计,用于实现对未处理序列的混淆和扩散,开发人员可自主选择使用哪种后处理扩展算法。下面,本节将详细介绍两种后处理扩展算法的设计方案。
1) 基于SM3的后处理扩展算法
基于SM3后处理算法的内部状态由变量V(比特串V,在每次调用SRNG时更新值),C(长度为440 bit的比特串C,为随机数发生器的内部状态变量)和counter(重播种计数器)组成,其中V和C长度相等。通过判断counter值,来确定是否更新种子(seed,初始化和更新RNG内部状态的变量)和内部状态。参考SRNG基本架构,基于SM3后处理扩展算法分为3个部分:初始化函数、种子更新函数和输出函数。
∙初始化函数
初始化函数用于对基于SM3后处理扩展算法的初始内部状态进行赋值。算法1展示初始化函数的伪代码,种子seed长度为440 bit(在不同密码应用场景中可调整种子长度),将未处理序列作为SM3_df函数的输入,可生成440 bit的种子数据。实验中我们根据EM-SRNG熵估计环节对主熵池数据的熵值计算结果来决定输入的未处理序列长度,以此保证初始化函数中的输入序列input有256比特熵。初始化函数第2~3行,将初始V值设定为调用SM3_df函数输入未处理序列返回的值,初始C设定为调用SM3_df函数输入16进制00和当前V值返回的结果。最后将重播种计数器的初始值设定为1。
|
|
算法2展示SM3_df的伪代码,SM3_df可用于生成种子、更新内部状态V和C。SM3_df函数第2~3行,计算要求返回的数据长度与SM3输出长度256的倍数关系,并将重播种计数器的值设为1。SM3_df函数第4~7行,根据返回数据长度与256的关系,循环用SM3算法产生中间数据temp,并将每次的temp拼接起来。最后,从中间数据temp值中从左到右读取要求返回长度的数据。
|
|
∙种子更新函数
种子更新函数用于更新基于SM3后处理扩展算法的种子seed,并更新内部状态V和C。算法3展示种子更新函数的伪代码,函数第1行,调用SM3_df函数来更新种子。种子更新函数第2~4行,更新V值为当前种子值,然后调用SM3_df函数输入16进制01和当前内部状态V值,返回结果是440 bit的C更新值,将重播种计数器值重设为1。
|
|
∙输出函数
随机数输出函数用来产生每次请求所需要的随机数据。算法4展示输出函数的伪代码,对V进行SM3运算生成256 bit的随机数。V的更新取决于前一时刻状态的V、C和counter值。
|
|
为提高内部状态的安全性,基于SM3后处理扩展算法每调用一次输出函数最多产生256 bit数据。当请求随机数长度小于256 bit时,会对数据进行截取;当请求随机数长度大于256 bit时,会循环调用输出函数,在每次调用输出函数后都会调用种子更新函数来输入新的熵,以此避免相同内部状态循环产生过多中间数据的安全隐患。
2) 基于SM4的后处理扩展算法
基于SM4后处理算法的内部状态由V(计数器)、Key(密钥)和counter(重播种计数器)组成,V和Key的长度均设为128 bit,与SM4算法标准的要求保持一致。参考SRNG基本架构,基于SM4后处理扩展算法亦分为3个部分:初始化函数、种子更新函数和输出函数。
∙初始化函数
初始化函数用于对基于SM4后处理扩展算法的初始内部状态Key、V和counter进行赋值。算法5展示初始化函数的伪代码,种子seed(初始化和更新RNG内部状态的变量)长度为256 bit,调用SM4_df函数生成种子数据。初始化函数第2~3行,将初始Key和V值设为0,将Key、V和种子seed作为SM4_CTR_Update函数的输入。
∙种子更新函数
算法8展示种子更新函数的伪代码,利用输入更新种子,继而更新的种子通过SM4_CTR_Update函数来更新Key和V,并将counter值重置为1。SM4_CTR_Update算法的第2行和第3行通过SM4加密算法保证缓冲区temp有256 bit数据。接下来,先缓冲区temp数据和外部输入的seed数据异或,然后在缓冲区存放中间结果(SM4_CTR_Update算法第6行)。最后,SM4_CTR_Update算法的第7~8行,缓冲区temp最左边的128 bit用来更新密钥K,剩余的128 bit用来更新V。
|
|
|
|
|
|
|
|
∙输出函数
算法9展示输出函数的伪代码,第1行将additional_input变量设置为0字符串。输出函数第2~4行中,计数器V递增,通过SM4算法密钥Key加密V来输出128 bit随机数,然后根据请求长度截取部分数据返回给应用程序。输出函数第5~6行中,调用SM4_CTR_Update函数输入additional_input、内部状态Key值和V值,返回结果Key和V的更新值,并将重播种计数器值加1。
此外,Cohney等[27]对NIST SP 800-90A中基于计数器工作模式的分组密码算法实现的确定性随机数发生器提出缓存攻击模式。为了提高安全性,本方案中基于SM4实现的后处理算法每调用一次输出函数最多产生128 bit数据。当请求长度超过128 bit时,会循环调用输出函数,而每次调用输出函数后都会立即更新内部状态,以此避免同一状态循环产生过多中间数据的安全隐患。
|
|
下面,对所设计的EM-SRNG进行安全性分析。
对于R1要求而言,我们所设计的软件随机数发生器从以下3个方面确保输出数据的质量。首先,纳秒级时间熵源产生的未处理序列对于外部观察者而言不可获知。一方面时间同步很难实现,另一方面读取的纳秒级时间存在不确定性的时间误差,此误差不受敌手和用户影响;其次,我们会对未处理序列进行熵测量来评估随机性;最后,经过熵检测达到预设熵阈值的数据,准许输出;对于熵不足的未处理序列,EM-SRNG工作机制会对数据执行后处理运算,以提升数据的统计性质和每比特的熵值。保证EM-SRNG输出的随机数有较好的统计特性。由此,EM-SRNG满足伪随机性要求。
对于R2要求而言,我们设计的EM-SRNG后处理模块实现了基于SM3和SM4的后处理算法。此外,由于LRNG输出函数采取先更新内部状态后输出随机数的状态更新策略,造成LRNG不提供前向安全性[7]。而基于SM3和SM4后处理扩展算法中的输出函数都是采用先输出随机数后更新内部状态的更新策略。由此,EM-SRNG满足前向安全性要求。
对于R3要求而言,我们设计的EM-SRNG的后处理模块包含种子更新函数,其作用是通过新输入的未处理序列更新SRNG中的种子以及内部状态。每次调用输出函数后,会立即执行种子更新函数。攻击者即使获取了某一时刻发生器的内部状态,但种子更新函数的输入数据会带来新的熵,使得攻击者难以准确预测出EM-SRNG之后时刻的内部状态信息,从而难以泄露之后时刻EM-SRNG的输出。由此,EM-SRNG满足后向安全性要求。
3 安全性和性能评价本章,对所设计的软件随机数发生器进行安全性和性能方面的评价,以验证该架构的可靠性和实用性。
3.1 实验平台本文设计的EM-SRNG实现在64位Ubuntu操作系统的台式机上,其系统版本为16.04.9,内核版本为4.4.0,编译器版本为5.4.0,内存为4 GB。LRNG熵池数据来源于64位Ubuntu操作系统的台式机上,其系统版本为16.04.11,内核版本为4.14.102,编译器版本为5.4.0,内存为4 GB。
3.2 EM-SRNG熵源质量 3.2.1 纳秒级时间熵源在实验中,我们观察了9位纳秒级时间序列,发现前4位重复数据过多,并存在一定规律性,而后5位数据的自相关性和均匀性较好,特别是最后一位数据其基本不相关。因此,最终选取纳秒级时间最后一位作为未处理序列。
在实验中,利用90B测量了1 000次纳秒级时间最后一位数据的比特熵,每次数据长度为106字节。如图 2所示,横坐标代表熵值范围(0~1),纵坐标代表频数,纳秒时间最后一位数据的比特熵集中在0.75~0.9。

|
Download:
|
| 图 2 纳秒时间末位数据比特熵 Fig. 2 Bit entropy of the last data in nanosecond time | |
为进一步提高未处理序列的质量,在保证输出速率的情况下,按固定间隔取纳秒级时间最后一位数据作为未处理序列。分别按间隔1、2、3、4位取数,重复实验500次。其平均比特熵结果如表 1所示,我们发现按固定间隔取数据会增加熵值。考虑到时间效率及比特熵增长情况,我们按固定3位数的间隔取纳秒级时间序列的最后1位数据作为未处理序列。
|
|
表 1 固定间隔数据的比特熵 Table 1 Bit entropy of fixed interval data |
实验对比测试了LRNG熵池数据的熵值。由于Linux内核源码对外开放,我们对Linux内核进行编译,将Linux用于填充熵池的元数据结构体作为系统日志信息填充至Linux的系统的环形缓冲区中,其中元数据结构体中包含jiffies(记录系统的时钟中断次数)、cycles(CPU时钟周期数)和num(熵源事件类型)3部分。经过对LRNG源码分析后,可知LRNG会先将元数据结构体的3部分数据进行拼接,然后将数据添加入熵池中。
利用Linux系统的dmesg命令配合过滤条件读取系统环形缓冲区中关于熵池元数据的特定内容并重定向至特定文件用于后续处理。对重定向文件进行分析,发现主熵池中jiffies数据以及num数据的重复率较高。由于Linux熵估计方法是对jiffies数据进行“3阶时间差”计算,过多重复jiffies值会造成某些熵源数据的熵值为0。
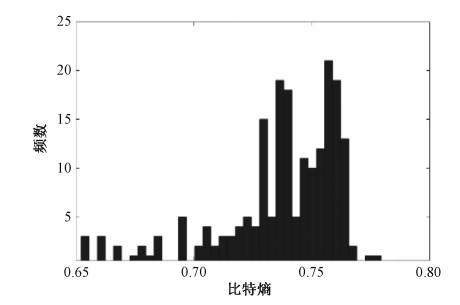
在实验中,我们观察LRNG主熵池的元数据,并通过NIST SP 800-90B测量了200组cycles数据的比特熵,每次数据长度为106字节,如图 3所示,发现cycles熵值集中在0.7~0.76。
|
Download:
|
| 图 3 LRNG熵池数据质量 Fig. 3 Data quality of LRNG entropy pool | |
根据3.2.1和3.2.2小节的分析,分别对纳秒级时间序列和LRNG熵池数据进行测量。从原理上分析,LRNG熵池中存在jiffies和num数据的重复率较高的问题,导致LRNG熵池中每条数据存在过多的冗余数据。虽然LRNG会通过确定性密码算法消除冗余数据的影响,但冗余数据依然会造成计算资源的浪费。而我们对纳秒级时间数据进行仔细分析和选取,尽量确保进入EM-SRNG熵池的数据不存在冗余数据。从实验结果分析,本方案中的熵源是纳秒级时间序列,按3位时间间隔只取纳秒级时间序列的最后一位,其比特熵平均值大约是0.883 1。我们亦对LRNG熵池中cycles变量值进行了测试,其比特熵集中在0.7~0.76。经实验数据分析可得,本方案中熵源质量高于LRNG的熵源质量。
3.3 EM-SRNG输出质量本文EM-SRNG熵判断环节的阈值设定为0.92(参考LRNG dev/urandom输出序列的熵值,在不同应用场景中可适当调整阈值),如果未处理序列比特熵达到0.92,那么直接作为随机比特输出。否则经过后处理模块处理后再输出。本方案后处理模块包括基于SM3的后处理算法和基于SM4的后处理算法。我们使用90B对EM-SRNG输出序列的比特熵进行重复测试,发现EM-SRNG中通过基于SM3后处理扩展算法和基于SM4后处理扩展算法输出序列的比特熵都集中在0.93~0.95。
LRNG为用户提供两个接口来获取随机数,在实验中我们利用90B测试了1 000次dev/urandom文件输出的106字节随机数的比特熵。如图 4所示,横坐标代表比特熵,纵坐标代表频数。可知dev/urandom输出数据的比特熵集中在0.92~0.94。由于LRNG非阻塞熵池和阻塞熵池的随机数输出原理有差异,dev/random数据来源于阻塞熵池,阻塞熵池输出要求是该熵池数据熵值达到阈值,而dev/urandom数据来源于非阻塞熵池,只要非阻塞熵池存在数据,那么dev/urandom数据就会存在。所以,可知dev/urandom读取随机数速率远远高于dev/random。由下文3.4小节分析得到的dev/random输出速率,从dev/random读取1 000字节随机数需要大约20 s。90B建议待测序列长度为106字节,而从dev/random读取106字节数据大约需要20 000 s(接近6 h)。由于从dev/random读取106字节数据所耗时间长,我们在实验中收集了从dev/random文件接口读取的10组100万字节数据,经过90B测试,其输出数据比特熵集中在0.94~0.95。

|
Download:
|
| 图 4 dev/urandom输出质量 Fig. 4 Output quality of dev/urandom | |
根据表 2总结可得,本文提出的EM-SRNG的随机数输出质量与LRNG dev/random提供的数据质量相当,而略好于LRNG的dev/urandom提供的数据质量。
|
|
表 2 对比EM-SRNG和LRNG的输出质量 Table 2 Comparison of EM-SRNG and LRNG output quality |
在输出质量得到保证的前提下,更快的随机数输出速率能够为用户提供更便捷的服务,及时满足对随机数的需求。为此,我们从随机数输出速率角度对性能进行综合评估。
本文EM-SRNG的随机数输出时间包括未处理序列的生成时间、90B在线熵估计环节时间和后处理模块(基于SM3后处理扩展算法和基于SM4后处理扩展算法)时间。在EM-SRNG输出100万字节随机数据的前提下,EM-SRNG按固定3位数间隔读取100万字节纳秒级时间序列末位数据大约需要8 ms时间,EM-SRNG熵监控模块中的90B熵估计环节大约需要2 s。基于SM3后处理扩展算法和基于SM4后处理扩展算法输出106字节数据时间集中在100~300 ms。由此,发现EM-SRNG输出100万字节随机数的时间主要消耗在熵监控模块,需要大约2 s的时间。
LRNG为用户提供接口获取随机数,用户可以通过读取dev/urandom文件或者dev/random文件来获取随机数。dev/random接口要求阻塞熵池的熵值达到阈值,然后再输出随机数据,为此dev/random输出随机数需要时间较长。图 5展示5 000次调用dev/random输出1 000字节随机数需要的时间,以μs为单位。从图 5中可以直观地看到dev/random产生1 000 bit时间大约是15~25 s。有少量时间高于或者低于15~25 s的范围,是由于dev/random的输出时间取决于LRNG主熵池数据达到阈值的时间,如果主熵池数据的熵值较快达到阈值,那么输出1 000字节的时间就会相应变短;反之,输出1 000字节的时间就会变长。

|
Download:
|
| 图 5 dev/random产生1 000 bit数据的时间 Fig. 5 Dev/random time to produce 1 000 bit of data | |
由于LRNG熵源事件频繁发生,导致添加到LRNG主熵池的jiffies时间数据重复率或者连续性较高。在这种情况下,LRNG“3阶时间差”熵估计方法计算的熵值会较低,造成阻塞熵池中熵计数器值增速较慢,最终影响到dev/random文件接口的输出速率。相比而言,dev/urandom输出速率总体远远高于dev/random输出速率。
EM-SRNG输出100万字节的随机数大约需要2 s,而dev/urandom文件接口输出100万字节数据大约仅需要10 ms,EM-SRNG输出速率慢于dev/urandom大约200倍。EM-SRNG在2 s时间内大约可以生成106字节的随机数据,而dev/random文件接口在2 s时间内大约可以生成100字节的随机数据,EM-SRNG输出速率快于dev/random大约104倍。LRNG非阻塞熵池输出随机数不考虑熵池数据的熵值,将非阻塞熵池数据经过确定性密码算法处理后生成的数据直接存储于dev/urandom文件中,而阻塞熵池利用熵阈值条件控制dev/random的输出。EM-SRNG和dev/random都通过熵阈值条件控制随机数的输出,而EM-SRNG输出速率远高于dev/random。EM-SRNG产生随机数的时间主要消耗在熵估计环节,如果EM-SRNG缺乏熵监控模块,那么其生成随机数的时间是未处理序列生成时间和后处理模块处理时间之和,则EM-SRNG与dev/urandom的输出速率属于同一量级。
在随机数输出速率方面,如表 3所示,EM-SRNG的数据产生速率比LRNG的dev/random高4个数量级左右,但由于在结构中嵌入了基于90B统计套件进行在线熵估计,使得EM-SRNG的速率比LRNG的dev/urandom要慢近200倍。如果EM-SRNG缺乏熵监控模块,那么其输出速率与LRNG的dev/urandom属于同一量级。综上分析可得,我们设计的EM-SRNG输出速率是较快的。
|
|
表 3 EM-SRNG与LRNG输出速率对比 Table 3 Comparison of EM-SRNG and LRNG output rates |
随着便携式物联网、智能移动终端等设备的不断普及,软件随机数发生器具有广阔的应用场景。然而,熵源的随机性不足以及SRNG内部状态的泄露会影响SRNG的安全性。为此,针对基于非物理源的软件随机数发生器的安全性设计,本文提出一种带有熵监控功能的软件随机数发生器(EM-SRNG)架构。EM-SRNG选用高精度纳秒时间作为熵源,并将纳秒时间的末位数据作为未处理序列,其具有良好的不可预测性和产生速率高的特点。并且,基于代码优化后的NIST SP 800-90B统计测试套件,EM-SRNG设计了嵌入式在线的熵估计器,可以对熵池数据质量进行实时地熵监测。随着商用密码算法的不断推广,EM-SRNG后处理模块基于中国SM系列密码算法设计而成,可选用基于SM3和SM4算法设计的两种后处理扩展算法。在实验方案中,我们对EM-SRNG进行了安全性和性能方面的评估,从熵源质量、输出质量和输出速率3个方面,对EM-SRNG和LRNG进行了对比分析。实验结果表明EM-SRNG可以提供良好的随机数服务。
| [1] |
Ma Y, Chen T, Lin J, et al. Entropy estimation for ADC sampling based true random number generators[J]. IEEE Transactions on Information Forensics and Security, 2019, 14(11): 2887-2900. Doi:10.1109/TIFS.2019.2908798 |
| [2] |
Varchola M. FPGA based true random number generators for embedded cryptographic applications[D]. Slovakia: Technical University of Kosice, 2008.
|
| [3] |
Von J Neumann. Various techniques used in connection with random digits[J]. National Bureau of Standards Applied Math Series, 1951, 12: 36-38. |
| [4] |
ISO/IEC 18031. Information technology-security techniques-random bit generation[S]. Berlin: International Organization for Standardization, 2011.
|
| [5] |
Li W, Chen H, Chen H. Research on ARM TrustZone[J]. Getmobile Mobile Computing & Communications, 2019, 22(3): 17-22. |
| [6] |
Ferraiuolo A, Baumann A, Hawblitzel C, et al. Komodo: using verification to disentangle secure-enclave hardware from software[C]//Proceedings of the 26th Symposium on Operating Systems Principles. New York: ACM, 2017: 287-305.
|
| [7] |
Gutterman Z, Pinkas B, Reinman T. Analysis of the linux random number generator[C]//IEEE Symposium on Security and Privacy. Oakland: IEEE, 2006: 371-385.
|
| [8] |
Strenzke F. An analysis of OpenSSL's random number generator[C]//Annual International Conference on the Theory and Applications of Cryptographic Techniques. Vienna: Springer, 2016: 644-669.
|
| [9] |
Kelsey J, Schneier B, Ferguson N. Yarrow-160: notes on the design and analysis of the yarrow cryptographic pseudorandom number generator[C]//International Workshop on Selected Areas in Cryptography. Kingston: Springer, 1999: 13-33.
|
| [10] |
Viega J. Practical random number generation in software[C]//Proceedings of the 19th Annual Computer Security Applications Conference Proceedings. Las Vegas: IEEE, 2003: 129-140.
|
| [11] |
Dorrendorf L, Gutterman Z, Pinkas B. Cryptanalysis of the random number generator of the windows operating system[J]. ACM Transactions on Information and System Security (TISSEC), 2009, 13(1): 1-32. |
| [12] |
Szor P. Return-to-LIBC attack blocking system and method: US, 7287283[P]. 2007-10-23.
|
| [13] |
Checkoway S, Davi L, Dmitrienko A, et al. Return-oriented programming without returns[C]//Proceedings of the 17th ACM conference on Computer and communications security. Chicago: ACM, 2010: 559-572.
|
| [14] |
National Institute of Standards & Technology. Recommendation for random number generation using deterministic random bit generators[S]. Gaithersburg: NIST Special Publication 800-90A, 2012.
|
| [15] |
Bernstein, Daniel J, Lange, et al. Dual EC:a standardized back door[J]. Journal of Neurosurgery Spine, 2015, 6(3): 256-281. |
| [16] |
牛佳敏. Dual_EC_DRBG算法后门事件及NSA在其中的角色[J]. 数据通信, 2015(3): 13-15. |
| [17] |
Killmann W, Schindler W. AIS 31: functionality classes and evaluation methodology for true (physical) random number generators[S]. Bonn: Bundesamt für Sicherheit in der Informationstechnik (BSI), 2001.
|
| [18] |
Barak B, Halevi S. A model and architecture for pseudo-random generation with applications to/dev/random[C]//ACM Conference on Computer & Communications Security. Chicago: ACM, 2005: 203-212.
|
| [19] |
National Institute of Standards & Technology. A statistical test suite for the validation of random number generators and pseudo random number generators for cryptographic applications[S]. Gaithersburg: NIST Special Publication 800-22, 2010.
|
| [20] |
L'Ecuyer P, Simard R J. TestU01:AC library for empirical testing of random number generators[J]. ACM Transactions on Mathematical Software (TOMS), 2007, 33(4): 22. |
| [21] |
Alani M M. Testing randomness in ciphertext of block-ciphers using DieHard tests[J]. IJCSNS International Journal of Computer Science and Network Security, 2010, 10(4): 53-57. |
| [22] |
国家密码管理局.信息安全技术二元序列随机性检测方法: GB/T 32915-2016[S].北京: 中国标准出版社, 2016.
|
| [23] |
National Institute of Standards & Technology. Recommendation for the entropy sources used for random bit generation[S]. Gaithersburg: NIST Special Publication 800-90B, 2018.
|
| [24] |
Hofmann O S, Dunn A M, Kim S, et al. Ensuring operating system kernel integrity with OSck[C]//ACM SIGARCH Computer Architecture News. New York: ACM, 2011, 39(1): 279-290.
|
| [25] |
Lee H, Moon H, Jang D, et al. KI-Mon: a hardware-assisted event-triggered monitoring platform for mutable kernel object[C]//Proceedings of the 22th USENIX Security Symposium. Washington DC: USENIX, 2013: 511-526.
|
| [26] |
Jiang F, Cai Q, Lin J, et al. TF-BIV: transparent and fine-grained binary integrity verification in the cloud[C]//Proceedings of the 35th Annual Computer Security Applications Conference. San Juan: ACM, 2019: 57-69.
|
| [27] |
Cohney S, Kwong A, Paz S, et al. Pseudorandom black swans: cache attacks on CTR DRBG[C]//IEEE Symposium on Security and Privacy (SP). San Francisco: IEEE, 2020: 750-767.
|
 2020, Vol. 37
2020, Vol. 37 


