2. 中国科学院大学材料与光电研究中心, 北京 100049;
3. 中国科学院力学研究所, 北京 100190
2. Materials and Photoelectric Research Center, University of Chinese Academy of Sciences, Beijing 100049, China;
3. Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China
高度不确定环境下的多属性决策问题是应急决策中需要面对的问题。Zadeh[1]提出的模糊集为模拟客观事物的不确定性提供了方法,然而决策者的认知不确定性逐渐成为影响决策结果的关键因素。目前,基于模糊理论的应急决策方法主要包括直觉模糊贝叶斯网络[2]、模糊神经网络[3]、F-TOPSIS(fuzzy technique for order preference by similarity to ideal solution)[4]和基于犹豫模糊语言术语集(HFLTS)的TODIM[5]等,这些方法为应急决策研究做出了贡献,但却较少关注高度不确定环境下语言决策信息的犹豫性、模糊性和非对称性,以及决策主体直观、快速的语言决策偏好问题[6-8]。
针对这一问题,本文提出一种基于模糊语言TOPSIS的多属性决策方法(multi-criteria decision-making method, MCDM),能够辅助决策者在应急情景下进行快速、准确的决策判断。该方法采用HFLTS[9]和二元语义[10]表达式对高度不确定环境下的语言进行处理,在提高对犹豫模糊语言信息提取能力的同时可生成决策者易于理解的语言评估结果,更加符合应急情景下决策主体的认知水平和表达习惯。此外,考虑到不确定环境下指标权重信息易缺失且指标间可能存在线性相关问题,对传统的欧氏距离TOPSIS进行改进,并采用基于离差最大化的马氏距离TOPSIS法确定评估指标的客观权重并对决策备选方案进行排序,在避免决策信息丢失的同时,使指标含义更加准确。最后,通过空中备降决策实例验证该方法的可行性与有效性。
1 基本假设 1.1 犹豫模糊语言集HFLTS以犹豫模糊集为基础,是指语言变量取值为语言术语集的一个有序且连贯的子集[9]。本文采用自由文本语法[11]将决策信息中的自然语言转化为HFLTS进行处理。
定义1 [9]设S={s0, …, sg}为语言术语集,GH=(VN, VT, I, P)为四元文本自由语法,现对GH定义如下:
| $ \begin{array}{l} \begin{array}{*{20}{l}} {\quad {V_N} = \{ 主词,复合词,一元关系,连}\\ {{\rm{词}}\} {\rm{ ; }}} \end{array}\\ \begin{array}{*{20}{l}} {\quad {V_T} = \{ “至多”,“至少”,“介于…之间”,{s_0},}\\ \begin{array}{l} {…},{s_g}\} {\rm{ ; }}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} I \in {V_N}; \end{array} \end{array} \end{array} $ |
| $ P = \left\{ {\begin{array}{*{20}{c}} I& \to &{{\rm{ 主词 or 复合词; }}}\\ {{\rm{主词}}}& \to &{{s_0}, \cdots ,{s_g};}\\ {{\rm{复合词}}}& \to &\begin{array}{l} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{一元关系}} + {\rm{主词}}\\ {\rm{二元关系}} + {\rm{连词}} + {\rm{主词}}}\ \ \ \ \ \ \ \ \ \ \end{array};\\ {{\rm{一元关系}}}& \to &{{\rm{ “至少” or “至多”; }}}\\ {{\rm{二元关系}}}& \to &{{\rm{ “介于…之间”; }}}\\ {{\rm{连词}}}& \to &{{\rm{ “和”; }}} \end{array}} \right\}. $ |
通过上述自由文本语法可生成表达式ll,并定义表达域ll=S。语言表达式可描述如下:
| $ \begin{array}{*{20}{l}} {l{l_1} = {\rm{至多是好; }}}\\ {l{l_2}{\rm{ = 介于好和完美之间。}}} \end{array} $ |
定义2[9] 设S为语言术语集,则定义犹豫模糊语言集HS有序有限且为S的连续语言术语子集:HS={si, si+1, …, sj}, sk∈S, k∈{i, …, j}。根据本文定义的语言术语集S,可有
| $ {H_S} = ({s_4},{s_5},{s_6}). $ |
定义3[9] 设EGH为比较语言表达式ll的转化函数,且ll∈Sll。现可将自由文本语法GH生成的Sll语言表达式集转化为HFLTS HS,即EGH:Sll→HS,包括
| $ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {E_{{G_H}}}({s_i}) = \{ {s_i}|{s_i} \in S\} ,\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {E_{{G_H}}}({\rm{ 至少 }}{s_i}) = \{ {s_j}|{s_j} \in S{\kern 1pt} {\rm{\& }}{\kern 1pt} {s_j} \ge {s_i}\} ,\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {E_{{G_H}}}({\rm{ 至多 }}{s_i}) = \{ {s_j}|{s_j} \in S{\kern 1pt} {\rm{\& }}{\kern 1pt} {s_j} \le {s_i}\} ,\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {E_{{G_H}}}({\rm{介于 }}{s_i}{\rm{ 和 }}{s_j}{\rm{ 之间 }}) = \{ {s_k}|{s_k} \in S{\kern 1pt} {\rm{\& }}{\kern 1pt} {s_i} \le \\ {s_k} \le {s_j}\} . \end{array} $ |
定义4[11] 令HS={si, si+1, …, sj}为HFLTS,且sk∈S, k∈{i, …, j},则有
| $ {\rm{env}}{ _F}({H_S}) = T(a,b,c,d). $ | (1) |
通过envF计算得到的模糊包络示例见图 1。
1.2 二元语义二元语义模型在传统模糊语言的基础上进行扩展,增加用于度量信息偏差的符号翻译参数α,能够在提升语言计算精度的同时避免计算过程中信息的丢失[10]。该模型可表示为(si, α)∈S≡S×[-0.5, 0.5),其中s∈S为语言术语,α∈[-0.5,0.5)。
定义5[13] 设S={s0, …, sg}为语言术语集,β∈[0, g]表示语言符号的集结数值,且二元语义等价于β,即
| $ \varDelta :[0,g] \to \bar S, $ | (2) |
| $ \varDelta (\beta ) = ({s_i},\alpha ),\left\{ {\begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {s_i},{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} i = {\rm{round}} (\beta ),}\\ {\alpha = \beta - i,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha \in [ - 0.5,0.5),} \end{array}} \right. $ | (3) |
| $ {{\varDelta ^{ - 1}}:\bar S \to [0,g],} $ | (4) |
| $ {{\varDelta ^{ - 1}}({s_i},\alpha ) = i + \alpha = \beta .} $ | (5) |
式中:round为四舍五入,i为β与符号si横坐标距离最近的索引值,Δ为映射函数。
2 基于改进型模糊语言TOPSIS的多属性决策方法 2.1 语言信息的集结根据基本假设,定义语言术语集S,使用转化函数EGH将决策者给出的语言表达式ll转化为基于HFLTS的HS。根据文献[12]所提方法,可采用OWA算子[14]将HS集成为基于梯形模糊数的模糊包络。
2.2 二元语义一致性转化使用二元语义变量对模糊包络进行一致性转化计算,转化过程可分为以下两个步骤:
步骤1 采用转化函数τ[15]将基于梯形模糊数的模糊包络转化为序偶表达式,即
| $ {\tau :T( \cdot ) \to F(S),} $ | (6) |
| $ {\tau ({t_i}) = \{ ({s_k},\gamma _k^i)|k \in \{ 0, \cdots ,g\} \} ,\forall {t_i} \in T( \cdot ),} $ | (7) |
| $ \gamma _k^i = \mathop {{\rm{max}}}\limits_y {\rm{min}} \{ {\mu _{{t_i}}}(y),{\mu _{{s_k}}}(y)\} . $ | (8) |
式中:T(·)为梯形模糊数,F(S)为模糊集S的正规集,μti(·)和μsk(·)为梯形模糊数中各点ti和语言术语sk对应集合S的隶属函数。
步骤2 采用翻译函数χ[15]将序偶表达式翻译为语言术语集S所在区间的实数值,然后再将这一实数值转化为二元语义变量,即
| $ {\chi :F(S) \to \bar S,} $ | (9) |
| $ {\chi (F(S)) = \varDelta \left( {\frac{{\sum\nolimits_{j = 0}^g j {\gamma _j}}}{{\sum\nolimits_{j = 0}^g {{\gamma _j}} }}} \right) = \varDelta (\beta ) = (s,\alpha ).} $ | (10) |
针对评估指标权重未知以及指标间易存在线性相关性的问题,本文提出一种基于离差最大化的马氏距离TOPSIS的多属性决策方法,使用基于离差最大化的赋权法确定各指标的客观权重,然后使用马氏距离TOPSIS法计算得到应急决策备选方案的排序。具体步骤如下:
步骤1 计算待评方案各指标值的离差与各方案指标的总离差
| $ {D_{ij}}(w) = \varDelta (\sum\limits_{k = 1}^n {{\varDelta ^{ - 1}}} {\rm{d}}[({s_{ij}},{\alpha _{ij}}),({s_{kj}},{\alpha _{kj}})]{w_j}), $ | (11) |
| $ {D_j}(w) = \varDelta (\sum\limits_{i = 1}^n {\sum\limits_{k = 1}^n {{\varDelta ^{ - 1}}} } {\rm{d}}[({s_{ij}},{\alpha _{kj}}),({s_{ij}},{\alpha _{kj}})]{w_j}). $ | (12) |
构造目标函数为全部方案总离差最大化的数学规划模型,即
| $ \begin{array}{*{20}{c}} {{\rm{max}}{\varDelta ^{ - 1}}D(w) = }\\ {\sum\limits_{j = 1}^n {\sum\limits_{i = 1}^n {\sum\limits_{k = 1}^n {{\varDelta ^{ - 1}}} } } {\rm{d}}[({s_{ij}},{\alpha _{ij}}),({s_{kj}},{\alpha _{kj}})]{w_j},} \end{array} $ | (13) |
| $ {\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{j = 1}^m {w_j^2} = 1,{w_j} \ge 0. $ | (14) |
步骤2 针对上述规划模型构造拉格朗日函数并求偏导,进行归一化处理后可得最优权重
| $ {w_j} = \frac{{\sum\limits_{i = 1}^n {\sum\limits_{k = 1}^n {{\varDelta ^{ - 1}}} } {\rm{d}}[({s_{ij}},{\alpha _{ij}}),({s_{kj}},{\alpha _{kj}})]}}{{\sum\limits_{j = 1}^m {\sum\limits_{i = 1}^n {\sum\limits_{k = 1}^n {{\varDelta ^{ - 1}}} } } {\rm{d}}[({s_{ij}},{\alpha _{ij}}),({s_{kj}},{\alpha _{kj}})]}}. $ | (15) |
步骤3 构建有n个备选方案和m个评估指标的初始语言决策矩阵Z
| $ \mathit{\boldsymbol{Z}} = {\{ ({s_{ij}},{\alpha _{ij}})\} _{n \times m}} = \left( {\begin{array}{*{20}{c}} {{z_{11}}}& \cdots &{{z_{1m}}}\\ \vdots &{}& \vdots \\ {{z_{n1}}}& \cdots &{{z_{nm}}} \end{array}} \right). $ | (16) |
用式(5)对初始语言决策矩阵Z中的元素进行转化,得到
| $ {z_{ij}} = {\varDelta ^{ - 1}}({s_r},\alpha ) = \beta . $ | (17) |
步骤4 确定评估指标值的正、负理想解
| $ {K^ + } = \{ (\mathop {{\rm{max}}}\limits_{1 \le i \le n} {z_{ij}}|j \in {G^ + }),(\mathop {{\rm{min}}}\limits_{1 \le i \le n} {z_{ij}}|j \in {G^ - })\} , $ | (18) |
| $ {K^ - } = \{ (\mathop {{\rm{min}}}\limits_{1 \le i \le n} {z_{ij}}|j \in {G^ + }),(\mathop {{\rm{max}}}\limits_{1 \le i \le n} {z_{ij}}|j \in {G^ - })\} . $ | (19) |
步骤5 计算决策评估对象zij到正、负理想解的加权马氏距离B+和B-,由式(15)得到评估指标权重矩阵
| $ {{B_i}^ + = \sqrt {({z_{ij}} - {k_j}^ + ){\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}^{\rm{T}}}{\mathit{\boldsymbol{C}}^{ - 1}}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}{{({z_{ij}} - {k_j}^ + )}^{\rm{T}}}} ,} $ | (20) |
| $ {{B_i}^ - = \sqrt {({z_{ij}} - {k_j}^ - ){\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}^{\rm{T}}}{\mathit{\boldsymbol{C}}^{ - 1}}\mathit{\boldsymbol{ \boldsymbol{\varOmega} }}{{({z_{ij}} - {k_j}^ - )}^{\rm{T}}}} .{\rm{ }}} $ | (21) |
计算得到各方案的相对贴近度,即决策评估值
| $ {L_i} = B_i^ - /(B_i^ + + B_i^ - ). $ | (22) |
步骤6 用式(3)将评估值转化为二元语义表达式,有
| $ \varDelta ({L_i}) = ({s_r},\alpha ). $ | (23) |
根据备选方案的评估结果,使用二元语义比较算子[10]进行排序。
需要注意的是,在使用马氏距离进行测度时,应避免出现以下两种情况[16]:1)行数n小于列数m;2)决策矩阵中数据标准差为0。
3 结果与讨论 3.1 空中备降应急决策空中备降是指飞行器在飞行过程中受不确定因素影响选择目的地以外机场降落的运行过程[17]。作为一类应急决策问题,受不确定因素发生的突然性和所导致后果的严重性影响,决策者需要在尽可能短的时间内做出准确的备降决策。
结合文献[17]中算例对本文所提方法进行验证。设备降航班为3U8834,备降场集合Z为{ZUUU, ZUMY, ZUNC, ZLXY, ZUZY, ZUGY},选取5个正向指标作为空中备降决策的评估指标,即:“地面保障能力”(G1),“备降机场相对距离”(G2),“备降机场能见度”(G3),“备降航路云高”(G4),“着陆操作复杂程度”(G5)。
3.2 备降方案求解现运用本文所提方法求解该空中备降决策问题,具体步骤如下:
步骤1 设决策评估指标的语言术语集S为
| $ S = \left\{ {\begin{array}{*{20}{l}} {{s_0}:{\rm{ 糟糕 }};{s_1}{\rm{ :差 }};{s_2}{\rm{ : 略差 }};{s_3}:{\rm{ 中等 }};}\ \ \ \ \ \ \ \ \\ {{s_4}:{\rm{ 略好 }};{s_5}:{\rm{ 好 }};{s_6}{\rm{ :完美 }}} \end{array}} \right\}. $ |
决策者可根据备降决策评估指标,使用基于自由文本语法的语言表达式对备选方案进行评估(受篇幅限制,不直接列出)。
步骤2 使用转化函数EGH将语言表达式ll转化为HFLTS并构造语言决策矩阵HS,见表 1。
|
|
表 1 语言决策矩阵 Table 1 Linguistic decision matrix |
步骤3 采用基于OWA算子的方法对语言决策矩阵中各元素进行集结,得到各元素的梯形模糊数,然后分别使用转化函数τ和翻译函数χ对其进行二元语义一致性转化,得到基于二元语义的决策矩阵,见表 2。
|
|
表 2 二元语义决策矩阵 Table 2 2-tuple linguistic decision matrix |
步骤4 通过式(15)确定评估指标的客观权重,见表 3。
|
|
表 3 基于2种不同方法所得的客观权重 Table 3 Objective weights of indexes determined using two different weighting methods |
步骤5 根据式(18)、式(19)得到各评估指标的正、负理想解,见表 4。
|
|
表 4 评估指标的正、负理想解 Table 4 Positive and negative ideal solutions of assessment indexes |
步骤6 使用加权马氏TOPSIS法对备降方案进行评估,并最终得到基于二元语义表达式的备降方案排序结果,见表 5。
|
|
表 5 空中备降方案相对贴近度和排序结果 Table 5 The relative similarities and ranking results of the flight alternate schemes |
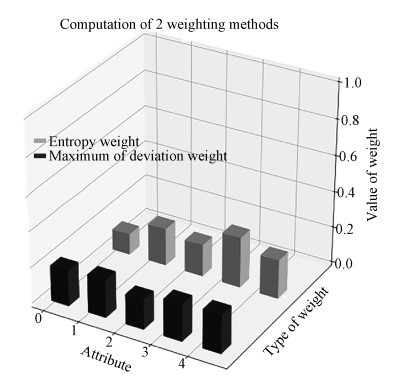
同时,采用熵权-欧氏TOPSIS、熵权-马氏TOPSIS和离差最大化-欧氏TOPSIS方法对该问题进行求解排序,所得结果见表 6,2种评估指标权重和4种决策排序结果如图 2和图 3所示。
|
|
表 6 基于3种不同方法的备降方案相对贴近度和排序结果 Table 6 The relative similarities and ranking results of the alternate schemes obtained using three different methods |
|
Download:
|
| 图 2 2种权重计算方法 Fig. 2 Two kinds of the weighting methods | |

|
Download:
|
| 图 3 4种多属性决策方法的排序结果 Fig. 3 Ranking results of four different MCDM methods | |
由表 6可知,采用不同的赋权方法时,若评估结果以β值计算,基于欧氏距离TOPSIS法所得相同方案的平均差值为0.062,其中方案3差值最大,为0.1;基于马氏距离TOPSIS法所得结果中同一方案平均差值为0.018,方案4差值最大,为0.03。可以看出,基于欧式距离测度时,受指标间相关性影响所得评估结果对权重变化的敏感度更高。相比之下,使用马氏距离TOPSIS法计算时各指标线性无关,使得评估结果对指标权重变化的敏感度较低。
3.4 二元语义对决策判断的影响由二元语义比较算子定义[10]可知,若二元语义中语言评价元素s的索引值更大,则评价结果更优;索引值相等时,α值更大的评价结果则更优。可见,二元语义作为一种定性定量结合的比较语言表达式,其比较算子的比较规则为先触发定性比较,再触发定量比较。
表 7中,以基于离差最大化的欧氏距离TOPSIS和马氏距离TOPSIS为例,2种方法均选择ZUUU为首选备降场,第2备降场分别为ZUNC和ZLXY。其中,欧氏距离TOPSIS法在评估排序中触发二元语义比较算子中的定性比较规则,而马氏距离TOPSIS法触发定量比较规则。
|
|
表 7 二元语义比较算子的使用 Table 7 The use of 2-tuple comparison operator |
由3.3节的讨论结果可知,基于欧式距离TOPSIS法的评价结果差值更大,更易触发比较算子中的定性比较规则,若加之决策者在决策判断过程中持有的乐观或悲观的决策偏好,可能会带来新的不确定性。因此,二元语义表达式更适用于马氏距离TOPSIS方法。
此外,本文所提方法在应用过程中仍需要关注以下两方面的问题:1)受TOPSIS自身测度的距离限制[18],可能导致各方案评估结果差值过小,不能反映备选方案的真正优势;2)对决策备选方案进行动态调整时,若新增方案非最优,或原非最优方案被更差的方案取代时,可能导致评估结果出现矛盾[18]。
4 结论本文所提方法实现了对应急决策备选方案定性与定量相结合的评估,能够辅助决策者在应急情景下进行快速、准确的决策判断,拓宽了模糊语言与TOPSIS的适用范围。
1) 采用犹豫模糊语言和二元语义表达式对语言决策信息进行处理,可提高对犹豫模糊语言信息的提取能力并得到易于理解的语言评估结果,降低应急情景下决策者的认知难度;
2) 在评估指标权重信息缺失或未知的情况下生成各指标的客观权重,且能够消除指标间的相关性,使含义更加准确;
3) 案例分析表明,本文所提方法操作简单且具有较好的实时性,所得首选备降场为ZUUU,评估结果为“中等,0.03”,验证了该方法的可行性与有效性,对于指导高度不确定环境下的应急决策实践具有重要意义。
| [1] |
Zadeh L A. The concept of a linguistic variable and its application to approximate reasoning[J]. Information Science, 1974, 8(3): 199-249. |
| [2] |
Hao Z N, Xu Z S, Zhao H, et al. A dynamic weight determination approach based on the intuitionistic fuzzy Bayesian network and its application to emergency decision making[J]. IEEE Trans Fuzzy Syst, 2018, 26(4): 1893-1907. Doi:10.1109/TFUZZ.2017.2755001 |
| [3] |
Simonovic S P, Ahmad S. Computer-based model for flood evacuation emergency planning[J]. Natural Hazards, 2005, 34(1): 25-51. Doi:10.1007/s11069-004-0785-x |
| [4] |
Fu G. A fuzzy optimization method for multi-criteria decision making:an application to reservoir flood control operation[J]. Expert Systems with Applications, 2008, 34(1): 145-149. Doi:10.1016/j.eswa.2006.08.021 |
| [5] |
Liang Y Y, Tu Y, Ju Y B, et al. A multi-granularity proportional hesitant fuzzy linguistic TODIM method and its application to emergency decision making[J]. International Journal of Disaster Risk Reduction, 2019, 36(2019): 101081. |
| [6] |
Vanderhaegen F. Erik Hollnagel:Safety-I and Safety-II, the past and future of safety management[J]. Cognition Technology & Work, 2015, 17(3): 461-464. |
| [7] |
Plioutsias A, Karanikas N. Using STPA in the evaluation of fighter pilots training programs[J]. Procedia Engineering, 2015, 128: 25-34. Doi:10.1016/j.proeng.2015.11.501 |
| [8] |
吴立珍, 李远, 彭辉, 等. 有人机/无人机协同任务指令集的设计与实现[J]. 系统仿真学报, 2008(S1): 514-517. |
| [9] |
Rodriguez R M, Martinez L, Herrera F. Hesitant fuzzy linguistic term sets for decision making[J]. IEEE Transactions on Fuzzy Systems, 2012, 20(1): 109-119. Doi:10.1109/TFUZZ.2011.2170076 |
| [10] |
Herrera F, Martinez L. A 2-tuple fuzzy linguistic representation model for computing with words[J]. IEEE Transactions on Fuzzy Systems, 2000, 8(6): 746-752. Doi:10.1109/91.890332 |
| [11] |
Rodríguez Rosa M, Martínez L, Herrera F. A linguistic 2-tuple multicriteria decision making model dealing with hesitant linguistic information[C]//2015 IEEE International Confer-ence on Fuzzy Systems (FUZZ-IEEE). IEEE, 2015: 1-7.
|
| [12] |
Liu H, Rodríguez R M. A fuzzy envelope for hesitant fuzzy linguistic term set and its application to multicriteria decision making[J]. Information Sciences, 2014, 258: 220-238. Doi:10.1016/j.ins.2013.07.027 |
| [13] |
Martinez L, Herrera F. An overview on the 2-tuple linguistic model for computing with words in decision making:extensions, applications and challenges[J]. Information Sciences, 2012, 207: 1-18. Doi:10.1016/j.ins.2012.04.025 |
| [14] |
Yager R R. On ordered weighted averaging aggregation operations in multicriteria decision making[J]. IEEE Trans Systems Man Cybernet, 1988, 18(1): 80-87. |
| [15] |
Herrera F, Martinez L, Sánchez P J. Managing non-homogeneous information in group decision making[J]. European Journal of Operational Research, 2005, 166(1): 115-132. |
| [16] |
Suo M, Zhu B, Zhang Y, et al. Fuzzy Bayes risk based on Mahalanobis distance and Gaussian kernel for weight assignment in labeled multiple attribute decision making[J]. Knowledge-Based Systems, 2018, 152: 26-39. Doi:10.1016/j.knosys.2018.04.002 |
| [17] |
王岩韬, 唐建勋, 赵嶷飞. 基于机位可调整的航班空中备降优化[J]. 安全与环境学报, 2018, 18(2): 636-639. |
| [18] |
Zavadsas E K, Mardani A, Turskis Z, et al. Development of TOPSIS method to solve complicated decision-making problems:an overview on developments from 2000 to 2015[J]. International Journal of Information Technology & Decision Making, 2016, 15(3): 645-682. |
 2020, Vol. 37
2020, Vol. 37 



