2. 中国科学院微小卫星创新研究院, 上海 201203;
3. 中国科学院大学, 北京 100049;
4. 上海科技大学, 上海 201210
2. Innovation Academy for Microsatellites, Chinese Academy of Siences, Shanghai 201203, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China;
4. ShanghaiTech University, Shanghai 201210, China
地面无线网络提供的移动通信服务仅覆盖有限的地理区域,而卫星网络可以扩大这些网络覆盖以提供全球通信服务,如飞行WiFi、巡航WiFi和偏远地区通信等。相比于高轨卫星轨道资源有限、功率开销大、信息传输时延长、卫星制造和发射成本高等诸多缺点,具有传输时延短、部署迅速、成本低、扩展性强等优点的低轨卫星通信网络,逐渐成为实现通信全球化、商业化、宽带化的重要解决手段[1]。为了提供全球通信服务,建立低轨卫星通信网络已引起学术界和产业界的广泛关注,如最近成为国外研究热点的OneWeb[2]、Space X[3]、Telesat、Leosat等系统。
低轨卫星成本低、体积小和重量轻的特点,造成低轨卫星的星上功率资源严重受限。由于轨道高度低,卫星运动速度快,使得低轨卫星的覆盖区域不断变化,面临的电磁环境复杂多变。另外,根据国际电联(ITU)和各国无线电管理部门的文件要求,高轨卫星通信的优先级要高于低轨卫星通信,导致低轨卫星在经过某些特殊区域时需要切换频率或者改变通信方向以规避对高轨卫星通信的干扰。同时,不同国家和地区的用户终端分布各不相同,不同用户终端的业务需求情况差异大,低轨卫星将面临动态变化的用户终端分布和业务需求情况。如何设计合理的资源调度策略,实现星上资源和业务需求之间的高效匹配,成为亟待解决的难题。目前国内外低轨卫星普遍使用传统固定多波束技术,该技术资源损耗大、星上功率利用率低,且对于用户非均匀分布的场景存在资源巨大浪费等缺陷。
跳波束技术是卫星通信领域最新的研究成果之一,该技术通过控制星载多波束天线的空间指向、带宽、频点和发射功率,为用户终端动态配置通信资源,提高卫星资源在带宽和功率方面的使用效率,为时域带宽分配提供了便利的平台。通过改变跳变波束在每个波束覆盖区的驻留时间,在有限星载资源条件下提高卫星宽带通信吞吐量,可以最大化星上带宽资源利用率[4]。基于多频时分多址(MF-TDMA)系统的平稳多波束资源管理算法比较成熟,可以根据用户服务需求动态调整带宽资源分配,从而在给定带宽资源的情况下有效提高系统容量[5]。文献[6]表明,跳波束技术可以提高卫星资源的带宽利用率和功率利用率。此外,跳波束技术可以通过将波束聚焦在目标位置来提高吞吐量并灵活利用卫星功率,这是一种十分有效的资源分配方式[7]。
调研发现,现有关于卫星跳波束的研究主要集中在高轨卫星,缺乏对低轨卫星的研究。欧洲航天局(ESA)于2004年对多波束卫星系统的波束跳变技术进行研究。美国休斯网络系统公司(HNS)在2007年使用该技术设计和建造了Sapceway-3宽带卫星通信系统[8],它以公平的轮询方式服务于每个小区单元。同时,许多美国专利也讨论了该技术的应用[9]。Pecorella等[10]设计一个可实现的跳波束系统架构,Anzalchi等[11]完成详细的系统仿真和性能对比以验证跳波束的优越性。Fonseca和Sombrin[12]提出一种更实用的基于小区复用机制的聚焦阵列跳波束馈源天线。近年来,跳波束技术与认知无线电技术的结合被认为是提高未来卫星系统频谱效率最有前途的研究方向[13]。
与高轨卫星相比,低轨卫星具有通信资源和业务需求动态变化的特点,使得基于高轨卫星的跳波束技术无法直接应用到低轨卫星通信系统。传统高轨跳波束技术波束跳变较慢且服务区域相对固定,而低轨卫星跳波束是比较快速的跳变,服务区域随卫星快速移动。从卫星整个覆盖区的角度来说,高轨卫星相对固定和缓慢,低轨卫星则相对复杂和快速。大量研究已显示出跳波束的技术优越性,但是现有技术仍然需要一种可用于低轨卫星的、基于跳波束技术的灵活的优化资源分配方案。
不仅如此,DVB-RCS2协议[14]提出动态调整频域带宽、DVB-S2X协议[15]从跳波束帧结构出发,论证了将跳波束技术应用于低轨卫星网络的实现可行性。本文基于低轨卫星快速移动场景,针对低轨卫星可用通信资源有限而业务需求分布动态变化时所面临的高效动态资源调度问题,提出低轨卫星宽波束结合动态点波束的跳波束接入方案,每颗卫星发射宽波束和点波束两种波束,由宽波束辅助点波束进行跳波束按需服务用户。仿真对比传统固定多波束方案与本文提出的宽波束结合动态点波束的跳波束接入方案,分析基于不同用户分布模式的归一化系统吞吐量、时延等性能。仿真结果表明,在用户分布极度不均匀的情况下,本文所提出宽波束结合动态点波束的跳波束方案在系统吞吐性能方面效果显著,比固定多波束方案更能充分利用星上有限资源。
1 系统建模 1.1 宽波束结合动态点波束的跳波束接入方案针对低轨卫星覆盖区内的波束覆盖方式,对卫星覆盖区进行资源建模。在传统的固定多波束覆盖方案基础上,提出宽波束与点波束结合的跳波束覆盖方案, 即使用宽波束结合动态点波束的跳波束宽带接入方案。宽波束又称为信令波束,负责整个卫星覆盖区信令和低速业务的传输,实现在网用户的在线管理和低速通信业务的基本需求;点波束又称为业务波束,由低速信令波束辅助一定数量的高增益点波束完成通信链路的建立。使用高增益的点波束实现全球任意区域可达来跟踪热点终端,以跳波束形式完成宽带高速业务的按需服务。
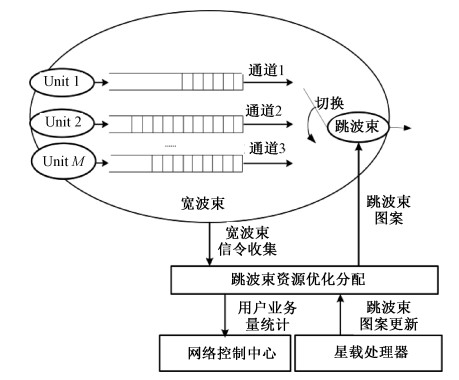
点波束采用高增益、窄覆盖、全球任意位置可达的设计思路,当地面热点终端数目小于星上能提供的最大点波束数目时,点波束采用一一对应方式对地面热点终端进行跟踪;当地面热点终端数目大于星上能提供的最大点波束数目时,点波束采用跳波束方式对地面热点终端进行跟踪。如图 1所示,本文主要讨论地面热点终端数目大于星上能提供的最大点波束数目时,以跳波束方式跟踪热点终端的方式,根据收集到的宽波束信令,统计用户业务量,通过星载处理器,更新跳波束图案,用来指导跳波束周期性时分复用的跟踪切换策略,完成对地面热点终端的按需服务。
|
Download:
|
| 图 1 宽波束结合动态点波束的跳波束接入模型 Fig. 1 Wide beam combined with spot beam hopping | |
跳波束策略的核心思想是时分覆盖的思想,网络控制中心通过收集宽波束的信令波束,系统可知各用户的通信需求,通过星载处理器根据需求制定跳波束图案,从而通过跳波束时分方式实现周期性波束服务。
与单波束覆盖相比,跳波束方案星上资源利用率更高,且允许比固定多波束覆盖更灵活地使用频率。相较于传统的多波束系统,使用跳波束技术,时间分片周期可以动态调整,能够适应变化的业务请求以及不均匀的业务分布,更好地适应动态时变的用户业务分布的需求,根据业务需求的实时变化,调整波束的覆盖区域和功率大小,从而更好地满足用户的业务需求,系统灵活性大大提高。从波束角度出发,对于固定多波束,由于其覆盖范围固定,一旦覆盖,不能调节,用户非均匀分布且用户数很少时存在波束无效覆盖的情况;而对于跳波束而言,由于其可以进行波束时域资源动态分配,其理论上的有效吞吐量利用率可达100%,但实际上因跳波束有同步开销、信令资源等多种开销,跳波束的“有效吞吐量”会下降。
1.2 卫星覆盖区小区模型为便于建模,将低轨卫星覆盖区可用多个整齐排列的矩形块进行划分,定义每个矩形块为一个小区(celli)。设卫星覆盖每一个celli的时间长度为T,每个celli内的用户数为numberi。对每一矩形celli进一步划分为若干M×N个等大小的点波束区域,定义每个波束区域为一个单元格,记为unitmn。
1.3 卫星覆盖区系统通信模型低轨卫星相对地球快速移动,相比高轨卫星其覆盖范围小、星间切换频繁、覆盖区域不断变化、多普勒频移大、卫星数目多、网络结构复杂、波束动态覆盖、动态通信资源和业务需求等情况更为复杂,低轨卫星通信面临着星上功率资源受限、频率资源和空间指向资源复杂多变、业务需求分布动态变化等众多严峻挑战。
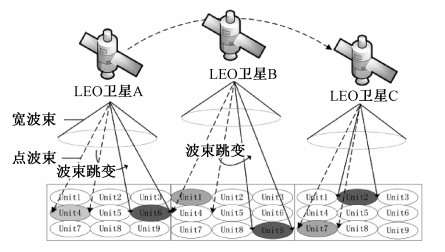
如图 2所示,建立低轨卫星宽波束结合动态点波束的跳波束接入方案系统通信模型。卫星端天线发射宽波束和点波束两种波束,通过采用宽波束与点波束相互配合的方案,即宽波束辅助引导下的跳波束切换,完成低轨卫星覆盖区的宽带通信。
|
Download:
|
| 图 2 低轨卫星跳波束方案系统模型 Fig. 2 System model of LEO satellite beam hopping scheme | |
小区celli内的每一个用户可以用userij表示,对第celli内用户编号为
| $ {\rm{use}}{{\rm{r}}_{ij}},j = 1,2, \cdots ,{\rm{numbe}}{{\rm{r}}_i}. $ | (1) |
单颗卫星的跳波束通过时分方式复用同样的频段,并参照Spaceway-3系统定义该波束组为链路复用组,不同链路复用组可以在空间上复用相同的频段。定义每个链路复用组中的波束最大数目为D,并在图 2中给出单星覆盖D=9组成的低轨卫星网络示意图。
1.4 卫星覆盖区业务建模低轨卫星通信系统的业务流量和地面网的业务流量不尽吻合,但两者均是非均匀分布的。一般而言,市区流量普遍高于郊区流量,发达地区流量普遍高于欠发达地区流量。这种不均匀性一方面是由用户密度不同造成的,另一方面是由各用户的业务量差异造成的。
1.4.1 用户的随机分布设目标区域celli中用户userij的位置坐标为(xuserij, yuserij),假定用户userij(xuserij, yuserij)在业务覆盖区celli内随机分布,二维随机变量(Xuserij, Yuserij)可服从均匀分布和二维正态分布[16]。
1) 均匀分布
若二维随机变量(Xuserij, Yuserij)具有概率密度函数
| $ f({x_{{\rm{ user}}{{\rm{ }}_{ij}}}},{y_{{\rm{ user}}{{\rm{ }}_{ij}}}}) = \left\{ {\begin{array}{*{20}{l}} {1/A,({x_{{\rm{ user}}{{\rm{ }}_{ij}}}},{y_{{\rm{ user}}{{\rm{ }}_{ij}}}}) \in {\rm{ cell}}{{\rm{ }}_i}}\\ {0,{\rm{ otherwise }}} \end{array}} \right., $ | (2) |
式中:celli为平面有界矩形域,面积为A。则用户(Xuserij, Yuserij)在celli上服从均匀分布。
2) 正态分布
设用户userij(xuserij, yuserij)的横纵坐标xuserij与yuserij相互独立,若二维随机变量(Xuserij, Yuserij)具有概率密度函数
| $ \begin{array}{l} f({x_{{\rm{ user}}{{\rm{ }}_{ij}}}},{y_{{\rm{ user}}{{\rm{ }}_{ij}}}}) = \\ \frac{1}{{2\pi {\sigma _1}{\sigma _2}}}{\rm{exp}}\left\{ { - \frac{1}{2}\left[ {\frac{{{{({x_{{\rm{use}}{{\rm{r}}_{ij}}}} - {\mu _1})}^2}}}{{\sigma _1^2}} + \frac{{{{({y_{{\rm{use}}{{\rm{r}}_{ij}}}} - {\mu _2})}^2}}}{{\sigma _2^2}}} \right]} \right\}, \end{array} $ | (3) |
则用户(Xuserij, Yuserij)服从参数为μ1, μ2, σ12, σ22, ρ=0的二维正态分布,记为
| $ ({X_{{\rm{ user}}{{\rm{ }}_{ij}}}},{Y_{{\rm{ user}}{{\rm{ }}_{ij}}}})\backsim N({\mu _1},{\mu _2},\sigma _1^2,\sigma _2^2,\rho = 0). $ | (4) |
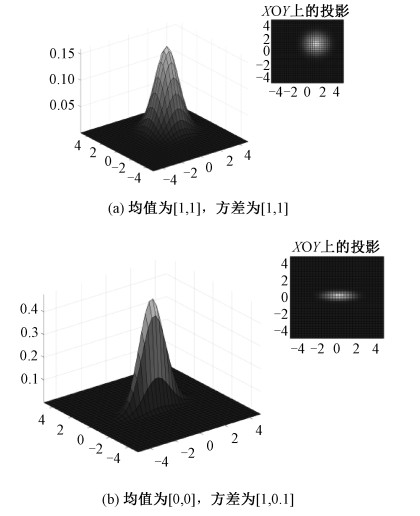
有界区域celli内所有用户userij正态分布的集中趋势位置坐标为(μ1, μ2),方差σ12和σ22分别描述用户userij在x轴和y轴上以正态分布的离散程度。图 3展示了正态分布的均值和方差对用户分布的影响。
|
Download:
|
| 图 3 正态分布均值和方差对用户分布的影响 Fig. 3 Influences of mean and variance of the normal distribution on user distribution | |
设目标区域celli中,userij的平均流量强度为Trafij(单位为bps),则celli中用户的业务流量可以建模成集合
| $ \mathbb{R} = \{ ({x_{{\rm{ user}}{{\rm{ }}_{ij}}}},{y_{{\rm{ user}}{{\rm{ }}_{ij}}}},{\rm{ Traf}}{{\rm{ }}_{{\rm{ user}}{{\rm{ }}_{ij}}}}),{\rm{ user}}{{\rm{ }}_{ij}} \le {\rm{ number}}{{\rm{ }}_i}\} , $ | (5) |
若(xuserim, yuserim)≠(xuserin, yuserin),则Trafuserim=≠Trafuserin(符号=≠表示不一定等于),即用户地理位置分布与用户平均流量强度没有直接等价关系。
这里的“用户”是地面热点终端,各个用户的品质因数G/T值有一定的差异。令Lp为链路功率损耗,EIRP为等效全向辐射功率,故链路载噪比C/T用dB的形式可以表示为
| $ C/T = {\rm{EIRP}} - {L_{\rm{p}}} + G/T, $ | (6) |
式中:G/T值、C/T值为用户专有参数,Lp已知,故式(6)可得表征用户userij的差异性的参数仅有EIRP值,表示为EIRPuserij;另外,用户userij的带宽需求为Buserij。从而,用户userij的属性向量为(EIRPuserij, Buserij),该属性与用户的平均流量强度为Trafij的关系可表示为
| $ {\rm{Traf}}{ _{ij}} = f( {\rm{EIRP}}{ _{{\rm{ user}}{{\rm{ }}_{ij}}}},{B_{{\rm{ user}}{{\rm{ }}_{ij}}}}). $ | (7) |
因此,celli中用户的业务流量可以等效地建模成为用户平均资源业务需求,表示为
| $ \begin{array}{*{20}{c}} {\mathbb{R} \Leftrightarrow \{ ({x_{{\rm{ user}}{{\rm{ }}_{ij}}}},{y_{{\rm{ user}}{{\rm{ }}_{ij}}}},{\rm{ EIR}}{{\rm{P}}_{{\rm{ user}}{{\rm{ }}_{ij}}}},{B_{{\rm{ user}}{{\rm{ }}_{ij}}}}),}\\ {{\rm{ user}}{{\rm{ }}_{ij}} \le {\rm{ number}}{{\rm{ }}_i}\} .} \end{array} $ | (8) |
至此,将目标区域celli中,非均匀用户分布模型建模成为用户的资源需求集合。
1.4.3 信道容量设在卫星覆盖的celli内,单颗卫星所能提供的跳波束个数为S。仅考虑波束间的资源分配问题,点波束覆盖范围比传统固定多波束更小,波束内的不同用户所经历的信道衰落更接近,故将波束内不同用户间的信道差异性进行统计平均,作为该波束的信道容量参量Cs,该处理方法已在多个文献中采用[17]。在每个时隙,系统依据信道传输特性的差异采用不同的信道传输速率,为方便建模起见,以理想的香农容量近似逼近卫星为每个unit提供的信道容量
| $ {C_{\rm{s}}} = B{\rm{log}}\left( {1 + \frac{{{\alpha _{\rm{s}}}P}}{{B{N_0}}}} \right), $ | (9) |
式中:B为跳波束系统的频域带宽,αs为波束s的信道衰减因子,N0为平均噪声功率谱密度,P为固定的等效下行传输功率(将天线增益折算在内)。
定义每一个unit的实际容量矩阵
| $ A = {\rm{min}}\{ R,C\} , $ | (10) |
式中:R为该unit中用户所需的容量矩阵:当一个unit中所有用户需求之和大于波束所能提供的容量时,此unit实际容量矩阵A=C;当一个unit中所有用户需求之和小于波束所能提供的容量时,此unit实际容量矩阵A=R。已知各波束的平均数据包到达速率λi,到达过程服从参数为λi的泊松随机过程。
1.4.4 目标函数与求解引入三维矩阵,可对应至一个X-Y-Z三维立体坐标, 目标函数为
| $ {\rm{max}}\sum\limits_{x = 0}^M {\sum\limits_{y = 0}^N {\sum\limits_{z = 0}^Z \mathit{\boldsymbol{E}} } } (x,y,z) * \mathit{\boldsymbol{A}}(x,y,z), $ | (11) |
式中:E(x, y, z)定义为跳波束分布矩阵,是达到目标函数须首先确认的优化矩阵,其每一项元素取值仅为0或1。当取值为1时所对应位置的unit被跳波束照射,取值为0时所对应的unit未被跳波束照射。其中1的个数即为卫星所能提供的总跳波束个数S,再加上一个时间维度z构成一个三维矩阵,其中z的取值为正整数,范围为[1, Z],其中Z=T/tunit, tunit为跳波束服务每一个unit的时间, 即Z为每一个跳波束服务unit的次数, 此处假设跳波束服务每个unit的时间一致。A(x, y, z)也是一个三维矩阵,其形式与E(x, y, z)一样,A矩阵元素每页取值对应于用户实际需求矩阵,再加上一个时间维度z构成三维矩阵。
由于低轨卫星快速移动导致其时间片分层较多,导致时间维度z是一个较复杂的因素,使得公式(11)的求解成为一个复杂的问题。本文提出一种迭代算法解决方案,如表 1所示。
|
|
表 1 系统算法解决方案 Table 1 Algorithmic solutions for the system |
为方便统计及简化计算,提出归一化系统吞吐量概念,来衡量跳波束方案与固定多波束方案的系统波束资源利用效率。归一化系统吞吐量是系统吞吐性能的集中体现,如其取值范围为[0, 1],当归一化系统吞吐量为1时,即系统吞吐量等于星上波束所能提供的总吞吐量,表示当前星上波束资源被最大化利用。
| $ {\rm{归一化系统吞吐量}} = \frac{{{\rm{系统吞吐量}}}}{{{\rm{星上波束所提供的总吞吐量}}}}. $ | (12) |
除系统波束资源利用效率外,还需要考虑的另一个重要参数是系统时延的分析,即数据包的总体延迟。在任何数据通信网络中,数据包都会由于传播时延、排队和缓存而产生系统时延,低轨卫星跳波束通信系统也不例外。卫星通信端到端的总延时由通信传输延时、数据处理延时和排队延时组成[18],其中通信传输延时取决于星地链路之间的距离,低轨卫星和高轨卫星由于轨道高度的不同,在对地通信传输延时差异较大。数据处理延时取决于星上载荷数据处理速度,一般可近似看作常数。排队延时是唯一可控的延时,若星上缓存足够大,排队延时的波动范围也将十分大。
数据包到达网关的总时迟可表示为
| $ {\tau _{{\rm{ delay }}}} = {\tau _{{\rm{ pgs }}}} + {\tau _{{\rm{ process }}}} + {\tau _{{\rm{ que }}}} + {\tau _{{\rm{ pld }}}} = {\tau _{{\rm{ que }}}} + {\tau _{{\rm{ ser }}}}, $ | (13) |
式中:τdelay为总时延,τpgs为通信传输延时,τprocess为数据处理延时,τque为排队延时,τpld为载荷固有延时。
本文仿真分析中,将排队时延等同于系统时延性能。对波束i的第p个数据包进行延时推导。数据包的驻留时间记为wisoj,其值等于数据包离开的时刻tif(p)与数据包到达时刻tia(p)之间的差值。平均排队时延即数据包驻留时间的统计平均值,也称为平均包驻留时间,可以通过平均包排队时间和平均包服务时间进行统计求和得到
| $ \begin{array}{l} E\left[ {w_i^{{\rm{soj}}}} \right] = \mathop {{\rm{lim}}}\limits_{K \to \infty } \frac{1}{K}\sum\limits_{p = 1}^K {\left[ {t_i^f(p) - t_i^a(p)} \right]} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = E\left[ {w_i^{{\rm{que}}}} \right] + E\left[ {w_i^{{\rm{ser}}}} \right] \le \varDelta , \end{array} $ | (14) |
式中:K为每个波束可服务的最大数据包数目,E[wisoj]为统计的波束i中的平均排队时延,E[wique]为统计的波束i中的平均包排队时间,E[wiser]为统计的波束i中的平均包服务时间,Δ为平均排队时延最大临界值(超出该临界值,则数据包重传)。
3 仿真结果与分析本文完成了对跳波束单星覆盖面积下cell的划分、unit中用户均匀与非均匀分布、跳波束方案和固定多波束方案性能对比等模型仿真。
3.1 仿真参数表 2为系统主要仿真参数。跳波束作为点波束,其覆盖范围小于传统固定多波束覆盖范围,在相同小区内,跳波束的单元格数目相应地远多于固定多波束的单元格数目。假设用户吞吐量需求总共有8个级别,分别为[2,4,8,12,16,24,32,64]×Kbps, 本文中K取值为300。
|
|
表 2 主要仿真参数 Table 2 Main simulation parameters |
图 4所示为跳波束与传统固定多波束方案基于用户分布均匀、用户分布非均匀分布下的归一化系统吞吐性能仿真图。可以看出,无论用户分布均匀与否,跳波束方案在系统吞吐性能方面效果都十分显著,归一化系统吞吐量都可以达到1,比固定多波束方案更能充分利用星上有限资源;在用户分布不均匀时,固定多波束方案最大归一化系统吞吐量值明显下降,由用户均匀分布时的0.98下降到0.47,可见当用户分布不均匀时,更能体现出跳波束方案在系统吞吐性能方面的优势。

|
Download:
|
| 图 4 跳波束方案与固定波束归一化系统吞吐量 Fig. 4 Throughput comparison between two schemes | |
跳波束方案能够按照用户需求进行资源分配,相比于传统固定多波束技术更为灵活。对于分布非均匀的用户,传统固定多波束方案受波束资源固定的限制,不能针对性满足不同用户分布的差异化需求,因此其系统吞吐性能相比于均匀分布明显下降,而跳波束方案优势则在用户非均匀分布时进一步体现出来,这是因为跳波束方案可以更好地适应用户需求,能更灵活地进行资源分配,从而实现最大归一化系统吞吐量值为1。
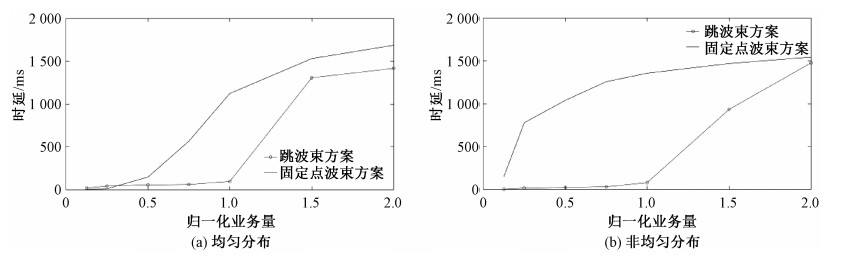
图 5所示为跳波束与传统固定多波束方案基于用户分布均匀、用户分布非均匀下的时延性能仿真图。可以看出,无论用户分布均匀与否,跳波束方案在系统时延性能方面效果都十分显著。当归一化业务量 < 1时,跳波束方案时延增长缓慢;当归一化业务量>1时,跳波束方案时延随着业务量累计而快速增长,在用户非均匀分布归一化业务量达到2时,跳波束方案时延性十分逼近固定多波束方案。
|
Download:
|
| 图 5 跳波束方案与固定波束时延性能对比 Fig. 5 Delay comparison between two schemes | |
固定多波束方案的系统时延,无论用户分布均匀与否,都随着系统归一化业务量的增长而增大,且受星上固定多波束数目所限,其时延有一定阈值,即当归一化业务量增长到一定值后,其时延不再增加。然而,跳波束方案,在业务量较小时,其系统时延也较小;但随着业务量的增长,跳波束方案每跳一次都有波束切换的时延累积,这就造成业务量较大时其系统排队时延也较大。
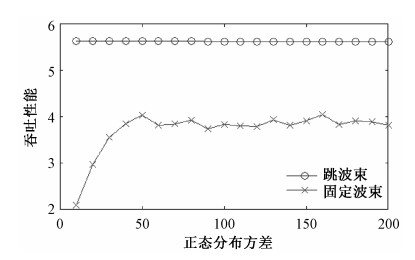
图 6所示为跳波束与固定多波束在用户正态分布情况下,不同方差所对应的系统吞吐性能。可以看出:在方差小于50,即用户分布极不均匀时,跳波束方案比固定多波束方案有更好的吞吐性能;在用户分布方差为10时,跳波束方案的吞吐性能是固定多波束方案的2.67倍; 在方差大于50之后,固定多波束系统吞吐性能在4左右动态波动,而跳波束方案吞吐性能基本保持不变,且一直大于固定多波束的吞吐性能。
|
Download:
|
| 图 6 跳波束方案对非均匀用户分布的适用性 Fig. 6 Applicability of the beam-hopping scheme for non-uniform user traffic distribution | |
用户分布由不均匀到相对均匀的过程中,跳波束的吞吐性能均远大于固定多波束,随着用户正态分布方差的减小,用户分布越不均匀,跳波束方案的优越性有了更好的体现。因此,本文提出的跳波束方案,是在用户分布不均匀情况下有较高优越性的高吞吐量方案。
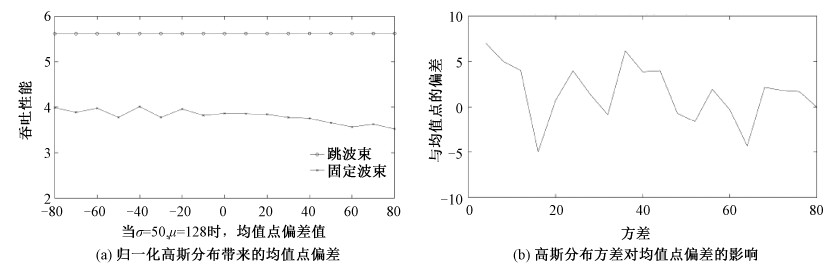
高斯分布的方差和均值分别取为σ1=σ2=50,μ1=μ2=128。仿真结果显示,归一化高斯分布会带来均值点偏差值。如图 7(a)所示,与图 6对应,可知仿真中的确存在高斯分布的均值点偏差,但影响范围不大(吞吐性能影响 < 0.5)。图 7(b)所示为找到的高斯分布的方差对均值点偏差的影响。
|
Download:
|
| 图 7 仿真带来的高斯分布对均值点偏差的影响 Fig. 7 Influences of Gaussian distribution on mean point deviation | |
因此,用户在卫星覆盖区域内的均匀分布和高斯分布,本质上都是一种随机分布,均匀分布的随机分布用户聚集度较低,高斯分布的用户聚集度与高斯分布的方差和仿真中归一化的均值偏差有关。表 3所示为跳波束与传统固定多波束方案基于用户分布均匀、用户分布非均匀下的系统最大吞吐性能、时延性能仿真总结。可以看出,在用户非均匀分布时,最能充分体现跳波束方案的优越性。此时,既能充分利用星上有限资源,系统最大吞吐性能为1,且有很好的时延性能。但随着业务量的增大,跳波束方案因波束切换而导致时延性能进一步退化。因此对于时延性能要求较高但用户吞吐量不大的业务(例如话音业务等),传统固定多波束依然有其价值所在。
|
|
表 3 仿真结论 Table 3 Simulation results |
本文从提高低轨卫星星上资源利用率角度出发,基于传统固定多波束技术,提出低轨卫星多波束技术最新研究成果——跳波束技术,将应用于高轨卫星的跳波束概念首次引入低轨卫星通信中。通过用户建模、业务建模等完成低轨跳波束卫星系统建模,使用归一化系统吞吐量、时延等系统指标进行分析,通过仿真结果理论上证明多波束最新技术——跳波束技术相对于固定多波束覆盖方案的优越性:1)通过时分复用周期性为用户按需提供服务,需要的波束较少,资源开销较低,星上资源利用率高,归一化系统吞吐量、时延性能与传统固定多波束方案相比,当用户非均匀分布时具有明显优势;2)可根据用户需求灵活分配系统无线资源,提高资源利用率。
由于低轨卫星快速移动导致波束切换、星间切换的复杂性,加上低轨卫星跳波束技术尚未成熟。下一步工作中,拟从星上跳波束波束跳变策略、用户实际业务需求分布、用户优先级分配等方面,考虑频率复用、干扰避免等实际问题,进一步开展低轨跳波束技术的研究。
| [1] |
Radtke J, Kebschull C, Stoll E. Interactions of the space debris environment with mega constellations:using the example of the OneWeb constellation[J]. Acta Astronautica, 2017, 131: 55-68. Doi:10.1016/j.actaastro.2016.11.021 |
| [2] |
Del Portillo I, Cameron B G, Crawley E F. A technical comparison of three low earth orbit satellite constellation systems to provide global broadband[J]. Acta Astronautica, 2019, 159: 123-135. Doi:10.1016/j.actaastro.2019.03.040 |
| [3] |
Heldmann J L, Stoker C R, Gonzales A, et al. Red dragon drill missions to mars[J]. Acta Astronautica, 2017, 141: 79-88. Doi:10.1016/j.actaastro.2017.10.002 |
| [4] |
Freedman A. Beam hopping system design considerations beam hopping: How to make it possible[C]//Ka and Broadband Communication Conference. Bologna: IEEE, 2015: 28-41.
|
| [5] |
Zhang T, Zhang L, Shi D. Resource allocation in beam hopping communication system[C]//2018 IEEE/AIAA 37th Digital Avionics Systems Conference (DASC)London: IEEE, 2018: 1-5.
|
| [6] |
Angeletti P, Prim F D, Rinaldo R. Beam hopping in multi-beam broadband satellite systems: system performance and payload architecture analysis[C]//24th AIAA International Communications Satellite Systems Conference(ICSSC). San Diago: IEEE, 2006: 11-14.
|
| [7] |
Mokhtar A, Azizoglu M. On the downlink throughput of a broadband LEO satellite network with hopping beams[J]. IEEE Communications Letters, 2000, 4(12): 390-393. Doi:10.1109/4234.898718 |
| [8] |
Whitefield D, Gopal R, Arnold S. Spaceway now and in the future: on-board IP packet switching satellte communication network[C]//IEEE Military Communications Conference. Washington: IEEE, 2006: 1-7.
|
| [9] |
Jacomb-Hood A W, Dentinger A M, Maalouf K J. Apparatus, method, and computer program products for cell-hopping satellite communications: US, 6522643B1[P/OL]. (2003-02-18)[2019-04-20]. https://www.freshpatents.com/-dt20150205ptan20150036540.php.
|
| [10] |
Pecorella T, Fantacci R, Lasagni C, et al. Study and implementation of switching and beam-hopping tchniques in satellites with on board processing[C]//2007 International Workshop on Satellite and Space Communications. Salzburg: IEEE, 2007: 206-210.
|
| [11] |
Anzalchi J, Couchman A, Gabellini P, et al. Beam hopping in multi-beam broadband satellite systems: System simulation and performance comparison with non-hopped systems[C]//2010 5th Advanced Satellite Multimedia Systems Conference and the 11th Signal Processing for Space Communications Workshop. Cagliari: IEEE, 2010: 248-255.
|
| [12] |
Fonseca N J G, Sombrin J. Multi-beam reflector antenna system combining beam hopping and size reduction of effectively used spots[J]. IEEE Antennas and Propagation Magazine, 2012, 54(2): 88-99. Doi:10.1109/MAP.2012.6230720 |
| [13] |
Sharma S K, Chatzinotas S, Ottersten B. Cognitive beamhopping for spectral coexistence of multibeam satellites[J]. International Journal of Satellite Communications and Networking, 2015, 33(1): 69-91. Doi:10.1002/sat.1073 |
| [14] |
Rohde C, Stadali H, Perez-Trufero J, et al. Implementation of DVB-S2X super-frame format 4 for wideband transmission[C]//International Conference on Wireless and Satellite Systems. Cham: Springer, 2015: 373-387.
|
| [15] |
Angelone M, Ginesi A, Re E, et al. Performance of a combined dynamic rate adaptation and adaptive coding modulation technique for a DVB-RCS2 system[C]//2012 6th Advanced Satellite Multimedia Systems Conference (ASMS) and 12th Signal Processing for Space Communications Workshop (SPSC). Baiona: IEEE, 2012: 124-131.
|
| [16] |
吴赣昌. 概率论与数理统计:理工类[M]. 5版. 北京: 中国人民大学出版社, 2017: 70-73.
|
| [17] |
Choi J P, Chan V W S. Optimum power and beam allocation based on traffic demands and channel conditions over satellite downlinks[J]. IEEE Transactions on Wireless Communications, 2005, 4(6): 2983-2993. Doi:10.1109/TWC.2005.858365 |
| [18] |
Altman E, Jimenez T. NS simulator for beginners[J]. Synthesis Lectures on Communication Networks, 2012, 5(1): 1-184. |
 2020, Vol. 37
2020, Vol. 37 


