合成孔径雷达(synthetic aperture radar, SAR)具有全天时、全天候成像等优点,是高分辨率对地观测的重要工具;对目标进行准确定位是SAR的重要用途之一[1],而SAR影像立体定位是获取目标点三维信息的有效手段,对于成像区域的DEM生成、正射影像图制作,地形图绘制以及军事目标的精准解译等方面具有重要的应用价值。
距离-多普勒(range-Doppler)模型[2],简称R-D模型,在SAR图像立体定位中得到了广泛的应用。R-D模型基于SAR侧视斜距成像和多普勒频移两个特点,利用距离方程和多普勒频移方程建立SAR斜距图像的像点坐标与雷达平台坐标之间的函数关系,具有明确的几何物理意义[3];如果SAR满足正侧视成像条件,则R-D模型可以简化为多普勒中心频移为零的F.Leberl公式[4]。
针对机载SAR图像立体定位问题,张红敏等[5-6]基于R-D模型设计利用单个地面控制点的SAR图像立体定位方案。除R-D模型之外,韦北余等[7]研究在无地面控制点的情况下,利用和差波束SAR图像直接对地面目标进行定位的方法,可获取地面目标的三维坐标信息。程春泉等[8]通过对SAR影像成像几何机理的分析,以传感器位置和姿态作为定向参数,构建了考虑多普勒参数的SAR影像距离-共面方程及基于该方程的SAR影像空中三角测量模型。
星载SAR图像定位目前普遍采用R-D模型,例如加拿大的RADARSAT-2雷达系统[9]、德国的TerraSAR-X雷达系统[10-12]以及中国自主研制的GF-3雷达卫星[13-14]。使用R-D模型进行定位时,影响定位精度的主要因素在于天线相位中心的位置和速度误差,此外SAR系统时间误差、大气传播延迟误差以及成像处理的引入误差也是影响SAR图像定位精度的重要因素;对于星载SAR系统而言,采用高精度的系统定标方法可显著降低上述系统性误差,例如标定后的GF-3卫星[14]雷达天线相位中心的位置精度可达到5 cm,速度精度为0.05 mm/s。降低卫星的系统误差对于提高图像定位精度至关重要。
与星载SAR相比,机载SAR的平台稳定性要差很多,尤其是小型的飞机平台在飞行时容易受惯导漂移、风速、风向以及空中气流的影响,使得飞行轨迹不再满足SAR成像时所需的匀速直线运动要求,因此机载SAR成像时需要做运动补偿以保证图像质量,但是运动补偿精度依赖于飞机平台的传感器精度;在没有安装POS系统时,飞机平台的位置及速度误差较大,如果单纯依赖飞机平台提供的实时数据去求解定位参数,则由于数据源存在较大误差且各参数之间存在相关性,对定位模型的参数解算提出了很高要求。
把R-D模型应用于机载SAR图像定位,模型中的多普勒频移条件方程说明了飞机平台的速度分量与雷达斜距分量的乘积是关于多普勒中心频率的函数;多普勒中心频率在成像处理过程中可估计,雷达斜距误差(距离延迟)可标定,因此飞机平台的位置误差和速度误差成为影响定位精度的主要因素。与雷达距离延迟不同,平台位置误差和速度误差受限于机载定位导航设备的精度,具有随机性和难以标定等缺点。本文使用成像区域内的3幅SAR图像进行立体定位,针对3幅图像中的同名像点建立距离方程组,在定位模型上使定位的误差因素局限于平台位置误差和雷达斜距误差,尽可能消除平台速度和多普勒频移参数估计等误差因素对定位精度的影响,有利于提高SAR图像无控制点立体定位精度。
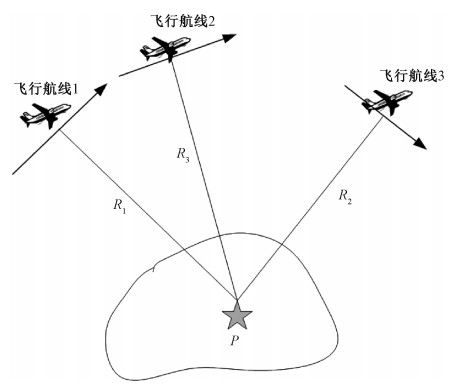
1 立体定位方法 1.1 定位基本原理假设机载SAR从3条不同的航线(非平行航线、相互交叉、夹角大于30°,如图 1所示)分别对目标区域进行条带模式成像,则目标位置坐标可由目标成像时刻雷达天线相位中心的位置坐标及其与目标之间的斜距距离确定,在地心坐标系下,目标点P的坐标与3条航线上对应的雷达天线相位中心坐标的几何关系可通过式(1)所示的距离方程组表达,求解式(1)所示方程组,即得到目标的三维坐标值,这一点同GPS定位原理类似。
| $ \left\{ {\begin{array}{*{20}{l}} {{f_1} = {{\left( {X - {X_1}} \right)}^2} + {{\left( {Y - {Y_1}} \right)}^2} + {{\left( {Z - {Z_1}} \right)}^2} - R_1^2 = 0, }\\ {{f_2} = {{\left( {X - {X_2}} \right)}^2} + {{\left( {Y - {Y_2}} \right)}^2} + {{\left( {Z - {Z_2}} \right)}^2} - R_2^2 = 0, }\\ {{f_3} = {{\left( {X - {X_3}} \right)}^2} + {{\left( {Y - {Y_3}} \right)}^2} + {{\left( {Z - {Z_3}} \right)}^2} - R_3^2 = 0.} \end{array}} \right. $ | (1) |
|
Download:
|
| 图 1 机载SAR通过3条航线对目标成像示意图 Fig. 1 Airborne SAR imaging through three air lines | |
式中:(X, Y, Z)为目标点的三维地心坐标,(X1, Y1, Z1)为飞行航线1的目标像点所对应的雷达天线相位中心坐标,(X2, Y2, Z2)为飞行航线2的目标像点所对应的雷达天线相位中心坐标,(X3, Y3, Z3)为飞行航线3的目标像点所对应的雷达天线相位中心坐标,R1、R2、R3为雷达天线相位中心至目标之间的斜距距离。雷达天线相位中心的经纬度坐标和海拔高度可通过机载卫星导航定位系统如GPS或者北斗获取,并可转换到地心坐标系,雷达天线相位中心至目标之间的斜距距离可通过雷达斜距测量确定。
由式(1)可见,当使用3条交叉航线所得SAR图像对目标进行定位处理时,目标的坐标值仅由雷达天线相位中心的坐标及目标与雷达之间的斜距距离决定,而与其他因素无关。如果雷达天线相位中心坐标、目标与雷达之间的斜距距离能够精确测量,则目标定位精度足够精确。该方法与R-D定位模型相比,至少使用3幅图像实现目标的立体定位,而R-D模型至少需2幅图像即可实现,但是R-D模型除距离方程外,还需多普勒频移方程;在多普勒频移方程中,飞机平台的速度误差和多普勒中心频率估计误差会对定位精度产生较大影响。
1.2 方程组求解式(1)所示方程组是一个非线性方程组,求解之前需要进行线性化,即把式(1)所示方程组进行泰勒展开,并保留0阶和1阶导数项,得到如式(2)所示的线性化方程组:
| $ \left\{ {\begin{array}{*{20}{l}} {{f_1} = f_1^0 + \frac{{\partial {f_1}}}{{\partial X}}\left( {X - {X_0}} \right) + \frac{{\partial {f_1}}}{{\partial Y}}\left( {Y - {Y_0}} \right) + \frac{{\partial {f_1}}}{{\partial Z}}\left( {Z - {Z_0}} \right) = 0, }\\ {{f_2} = f_2^0 + \frac{{\partial {f_2}}}{{\partial X}}\left( {X - {X_0}} \right) + \frac{{\partial {f_2}}}{{\partial Y}}\left( {Y - {Y_0}} \right) + \frac{{\partial {f_2}}}{{\partial Z}}\left( {Z - {Z_0}} \right) = 0, }\\ {{f_3} = f_3^0 + \frac{{\partial {f_3}}}{{\partial X}}\left( {X - {X_0}} \right) + \frac{{\partial {f_3}}}{{\partial Y}}\left( {Y - {Y_0}} \right) + \frac{{\partial {f_3}}}{{\partial Z}}\left( {Z - {Z_0}} \right) = 0.} \end{array}} \right. $ | (2) |
式中,令ΔX=X-X0,ΔY=Y-Y0,ΔZ=Z-Z0,改写成矩阵形式如下:
| $ \left[ {\begin{array}{*{20}{l}} {\frac{{\partial {f_1}}}{{\partial X}}}&{\frac{{\partial {f_1}}}{{\partial Y}}}&{\frac{{\partial {f_1}}}{{\partial Z}}}\\ {\frac{{\partial {f_2}}}{{\partial X}}}&{\frac{{\partial {f_2}}}{{\partial Y}}}&{\frac{{\partial {f_2}}}{{\partial Z}}}\\ {\frac{{\partial {f_3}}}{{\partial X}}}&{\frac{{\partial {f_3}}}{{\partial Y}}}&{\frac{{\partial {f_3}}}{{\partial Z}}} \end{array}} \right] \times \left[ {\begin{array}{*{20}{l}} {\Delta X}\\ {\Delta Y}\\ {\Delta Z} \end{array}} \right] + \left[ {\begin{array}{*{20}{l}} {f_1^0}\\ {f_2^0}\\ {f_3^0} \end{array}} \right] = \left[ {\begin{array}{*{20}{l}} {{f_1}}\\ {{f_2}}\\ {{f_3}} \end{array}} \right]. $ | (3) |
采用牛顿迭代法求解式(3)所示方程组,需先设定(X, Y, Z)的初始值为(X0, Y0, Z0),由于存在平台位置误差和距离误差,无法得到线性方程组的精确解,因此采用线性方程组的最小二乘解法求得改正量(ΔX, ΔY, ΔZ),则(X, Y, Z)的修正值为X′=X0+ΔX、Y′=Y0+ΔY、Z′=Z0+ΔZ,当(ΔX, ΔY, ΔZ)较大时,可令当前的(X′, Y′, Z′)值作为新的初值,重复求解式(3)所示方程组,求出新的(ΔX, ΔY, ΔZ)与(X′, Y′, Z′),上述求解过程反复迭代,直到(ΔX, ΔY, ΔZ)满足所要求的精度为止。迭代初值设为(0, 0, 0)即可得到优化的结果。
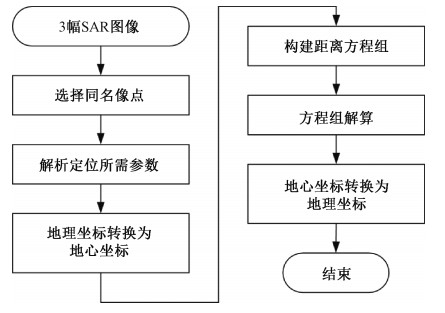
1.3 定位实现流程图 2给出利用交叉航线得到的3幅SAR图像进行立体定位的实现流程。
|
Download:
|
| 图 2 立体定位流程图 Fig. 2 Flow chart of stereo positioning | |
1) 在3幅图像中选择定位目标点对应的同名像点,得到目标点在3幅图像中对应的像素坐标;
2) 分别针对3幅图像,解析目标点像素所在方位线对应的辅助数据,得到雷达平台的经度、纬度、海拔高度以及图像近距对应的雷达斜距值R0,由同名像点的像坐标(x, y)和距离向采样间隔Mx,求得同名像点与雷达平台的斜距距离R=R0+x·Mx;
3) 将得到的雷达平台经度、纬度和高度值等转换到地心坐标系,并构建如式(1)所示的距离方程组;
4) 对方程组进行线性化,解线性方程组,得到最小二乘法解,即为目标点在地心坐标系下的坐标值;
5) 将目标点在地心坐标系下的值转换到地理坐标系,完成三维立体定位。
2 误差因素分析由式(1)的定位模型可以看出,采用3幅SAR图像进行立体定位时,影响SAR图像定位精度的直接因素是雷达平台的位置误差和雷达斜距误差(距离延迟);其中平台位置误差取决于机载导航定位系统的精度水平,可进一步细分为平台位置误差(经纬度误差)和平台高度误差;雷达斜距误差取决于雷达系统数据采集的时间精度以及大气传输延迟。下面分别通过实例仿真来分析平台位置误差、高度误差、雷达距离延迟等3个参数的测量误差对定位精度的影响,仿真使用的参数见论文第3节第1段。
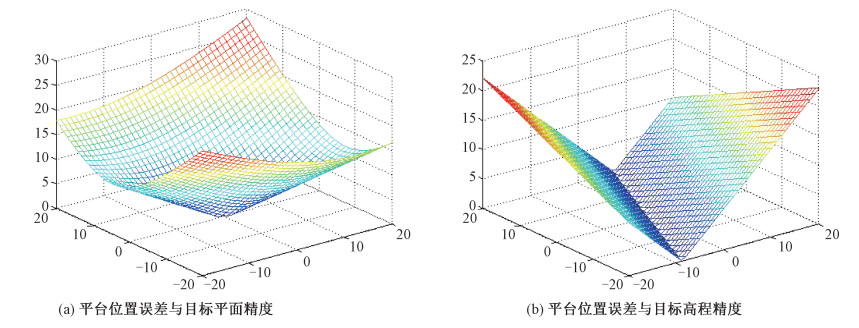
图 3给出平台位置误差与目标定位精度的关系曲面,由于目标定位误差是由多种误差因素共同作用的结果,为了模拟平台位置误差对定位精度的影响,本文假设平台高度和雷达斜距不存在误差,相当于对影响定位精度的耦合误差因素做简化处理,后面的处理方式均与此类似。图 3中平台位置误差的范围为[-20, 20]m,可以看出平台位置误差不仅影响目标的平面精度,对目标高程精度也有较大的影响。
|
Download:
|
| 图 3 平台位置误差对定位精度的影响 Fig. 3 Influence of position error of platform on positioning accuracy | |
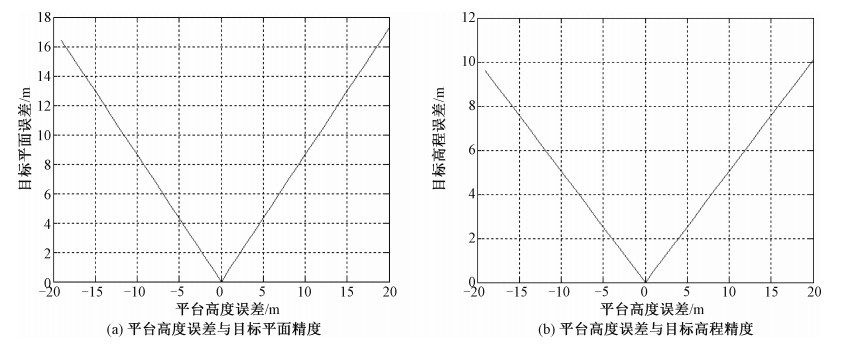
图 4给出平台高度误差与目标定位精度的关系曲线,这是假定平台位置误差和雷达斜距误差为0时所得到的结果。由图 4可见,平台高度误差对目标的平面精度和高程精度均产生影响,并且对目标平面精度的影响较大。
|
Download:
|
| 图 4 平台高度误差对定位精度的影响 Fig. 4 Influence of altitude error of platform on positioning accuracy | |
图 5给出雷达距离延迟与目标定位精度的关系曲线,这里假设平台位置误差和平台高度误差均为0。由图中可见,雷达距离延迟对目标平面精度的影响较小,当距离延迟在[-20, 20]m范围内变化时,目标平面误差最大值为1.1 m;与之相反的是,距离延迟对目标高程精度的影响甚为显著,[-20, 20]m范围内的斜距误差会导致最大72 m的目标高程误差。

|
Download:
|
| 图 5 雷达距离延迟对定位精度的影响 Fig. 5 Influence of range delay error of radar on positioning accuracy | |
综合图 3~图 5的仿真结果可以看出,对目标平面精度影响最大的误差因素是平台位置误差,对目标高程精度影响最大的因素是雷达距离延迟。值得一提的是,虽然经过标定后,雷达距离延迟可以很小,但是如果飞行过程中飞机姿态不稳定并且机载雷达位置坐标(由机载导航设备测量得到)存在较大误差,依然会造成SAR图像上的目标到雷达的斜距距离有不可忽略的误差值,从而造成目标高程精度降低。
3 试验结果与分析定位试验采用的SAR图像是由中国科学院电子学研究所研制的某试验型机载SAR系统获取的详查模式图像。雷达从3条不同的航线分别对同一目标区域成像,3条航线对应的航迹角分别为65.96°、128.83°和10.61°,雷达作用距离为近距10 km,飞机飞行高度3 100 m,飞行地速40 m/s,正侧视条带成像,所得3幅图像的有效重叠率为30%。雷达平台的实时位置坐标由GPS测量得到,该GPS没有采用差分定位,定位误差在2~10 m;经过标定后的雷达距离延迟小于1 m。
在3幅SAR图像中分别选择10个同名目标点用于定位测试,选择含有楼房、电线杆、平地角点等标志物的像素作为定位目标点,目标点的经纬度坐标和高程事先由GPS测量得到。
按照第1.3节所述的3幅图像联合立体定位的实现流程进行同名点选择、辅助数据解析和三维坐标解算,得到目标点的经纬度坐标和高程值,结果如表 1所示;表 2同时给出采用R-D模型[5]的立体定位结果,R-D定位模型采用2幅SAR图像,由于是正侧视成像,R-D模型中的多普勒中心频率参数设置为0。应保密要求,经纬度坐标的中间两位数字以“**”代替。
|
|
表 1 本文所提方法的立体定位结果 Table 1 Stereo positioning results of the proposed method |
|
|
表 2 采用R-D模型的立体定位结果 Table 2 Stereo positioning results of the R-D model |
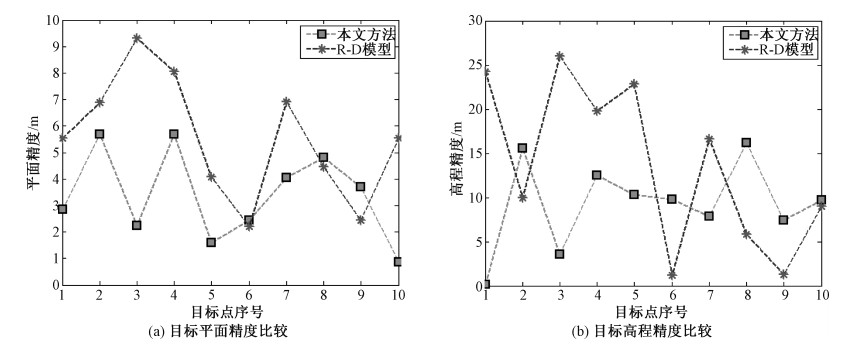
利用表 1和表 2中的数值,可得到本文方法与R-D定位模型的立体定位误差曲线,分别如图 6(a)、6 (b)所示。图 6(a)给出两种方法的目标平面精度比较,6(b)给出两种方法的目标高程精度比较。依据表 1和表 2中数值,计算得到本文方法与R-D模型所得定位误差的均方根值(RMS)如表 3所示。由图 6和表 3可以看出,本文方法的平面精度和高程精度总体上优于R-D模型。对于R-D模型来说,除雷达平台的位置误差、斜距误差外,还引入了飞机的速度误差以及多普勒中心频率估计误差。由于机载SAR成像运动补偿的影响,导致在图像中的某些点距离误差较大,影响了定位精度,使得图 6中的少数点采用R-D模型定位时精度占优。
|
Download:
|
| 图 6 两种模型定位精度的比较 Fig. 6 Comparison of positioning accuracy between two models | |
|
|
表 3 两种模型定位精度的RMS值比较 Table 3 Comparison of RMS value of positioning accuracy between two models |
R-D定位模型在星载SAR图像定位中得到了广泛应用并取得了很好的结果,机载SAR的平台稳定性远不如星载SAR,表现在速度、航迹的实时变化比较大。对于R-D模型来说,多普勒频移条件方程中的速度和多普勒中心频率参数在机载SAR图像定位时会成为影响定位精度的重要因素,在速度误差难以标定的前提下,如果只使用SAR辅助数据中的平台轨道参数而不采用地面控制点解算定向参数,则R-D模型针对机载SAR的无控制点定位误差较大,尤其是高程误差。
与R-D模型采用2幅SAR图像进行立体定位不同,本文使用成像区域不同航线所对应的3幅SAR图像进行联合立体定位,针对3幅图像中同一目标点所对应的同名像点建立距离方程组,多普勒频移条件方程则舍弃不用,在定位模型中仅需要知道平台的位置、高度和雷达的斜距距离即可完成定位解算。与R-D模型相比,本文方法可以减少定向参数并降低参数误差对定位精度的影响,代价为多使用1幅SAR图像参与定位解算。
本文采用3幅机载SAR条带模式图像进行立体定位的方法探索,并针对实飞的SAR条带图像进行定位试验,结果验证了方法的有效性。由于缺少聚束模式的试验数据,无法验证本文方法在聚束模式或者聚束与条带模式混合情况下的定位精度,这也是后续研究的方向。
| [1] |
潘志刚, 潘卓, 曹舸. 机载SAR无控制点直接定位方法[J]. 中国科学院大学学报, 2015, 32(4): 536-541. |
| [2] |
Curlander J C. Location of pixels in space-borne SAR imagery[J]. IEEE Transactions on Geosciences and Remote Sensing, 1982, 20(3): 359-364. |
| [3] |
Johnsen H, Lauknes L, Guneriussen T. Geocoding of fast-delivery ERS-1 SAR image mode product using DEM data[J]. International Journal of Remote Sensing, 1995, 16(11): 1957-1968. Doi:10.1080/01431169508954532 |
| [4] |
Leberl F W. Radargrammetric image processing[M]. Massachusetts: Artech House, 1990.
|
| [5] |
张红敏. SAR图像高精度定位技术研究[D].郑州: 信息工程大学, 2013.
|
| [6] |
张红敏, 靳国旺, 徐青, 等. 利用单个地面控制点的SAR图像高精度立体定位[J]. 雷达学报, 2014, 3(1): 85-91. |
| [7] |
韦北余, 朱岱寅, 吴迪, 等. 一种基于和差波束的机载SAR定位方法[J]. 电子与信息学报, 2013, 35(6): 1464-1470. |
| [8] |
程春泉, 张继贤, 黄国满, 等. 考虑多普勒参数的SAR影像距离-共面方程及其定位[J]. 遥感学报, 2013, 17(6): 1444-1450. |
| [9] |
Schubert A, Small D, Jehle M. COSMO-Skymed, TerraSAR-X, and RADARSAT-2 geolocation accuracy after compensation for earth-system effects[C]//2012 IEEE International Geoscience and Remote Sensing Symposium (IGARSS2012), Germany, 2012: 3301-3304.
|
| [10] |
Gisinger C, Balss U, Pail R, et al. Precise three-dimensional stereo localization of corner reflectors and persistent scatters with TerraSAR-X[J]. IEEE Transactions on Geosciences and Remote Sensing, 2015, 53(4): 1782-1802. Doi:10.1109/TGRS.2014.2348859 |
| [11] |
Eineder M, Minet C, Steigenberger P, et al. Imaging geodesy:toward centimeter-level ranging accuracy with TerraSAR-X[J]. IEEE Transactions on Geosciences and Remote Sensing, 2011, 49(2): 661-671. Doi:10.1109/TGRS.2010.2060264 |
| [12] |
Cong X Y, Balss U, Eineder M. Imaging geodesy:centimeter-level ranging accuracy with TerraSAR-X:an update[J]. IEEE Geoscience and Remote Sensing Letters, 2012, 9(5): 948-952. Doi:10.1109/LGRS.2012.2187042 |
| [13] |
云菲. 高分三号卫星[J]. 卫星应用, 2016(8): F0004. |
| [14] |
丁赤飚, 刘佳音, 雷斌, 等. 高分三号SAR卫星系统级几何定位精度处探[J]. 雷达学报, 2017, 6(1): 11-16. |
 2020, Vol. 37
2020, Vol. 37 


