2. 中国科学院大学, 北京 100049;
3. 中科卫星应用德清研究院 微波目标特性测量与遥感重点实验室, 浙江 湖州 313200;
4. 北京建筑大学, 北京 100044
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Laboratory of Target Microwave Properties, Deqing Academy of Satellite Applications, Huzhou 313200, Zhejiang, China;
4. Beijing University of Civil Engineering and Architecture, Beijing 100044, China
近几年来,地震、海啸等自然灾害日益频繁,给社会和国家造成了巨大的财产损失。研究表明,建筑物损毁引起的人员伤亡约占总伤亡人数的95%,因此,建筑物损毁评估是灾后信息调查的重点工作内容。自然灾害发生后往往伴随着云雨等恶劣天气,限制了光学遥感技术的应用,而合成孔径雷达(synthetic aperture radar, SAR)具有全天时、全天候对地观测的特点[1],在灾后应急救援和灾后建筑物损毁评估等方面具有明显优势[2]。
由于全极化SAR图像包含的极化信息非常丰富,如何合理地将极化特征运用到灾后建筑物损毁信息提取上成为研究的重点[3-5]。利用灾前灾后SAR数据进行损失评估的研究较多,但这类方法要求已经拥有同一区域的灾前SAR数据,这在某些情况下限制了该类方法的应用,因此利用灾后单一时相SAR数据对建筑物损毁检测和评估具有非常强的实用性。Wang等[6]利用高分辨率COSMO-SkyMed图像通过三角棱柱法计算震后SAR图像的分维值,并将计算结果与高分辨率光学图像进行比对,表明高分维值对应建筑物损毁严重区域,进而对建筑物损毁情况进行评估。Guo等[7]利用RADARSAT-2全极化数据,用圆极化相关系数ρRRLL、二次散射分量Pd和各向异性度A提取汶川地震后的倒塌建筑物,并与高分辨率光学图像进行对比,证明该方法的有效性。Li等[8]利用RADARSAT-2数据,根据圆极化相关系数与倒塌建筑物的相关性,提出基于极化参数H-α-ρ的震后倒塌建筑区提取方法。Zhang等[9]对RADARSAT-2极化数据利用最优极化对比度增强法,检测玉树地震中的损毁建筑物,并证明该方法对具有一致取向角的建筑物区域效果更好。可见,极化分解可以提取损毁建筑物的显著特征,因此有利于建筑物损毁评估。本文首先利用Yamaguchi分解和Touzi分解分析损毁建筑物的散射机制和特征,然后将显著散射特征进行组合,对灾后极化SAR图像进行视觉优化,进而快速识别出不同损毁程度的建筑物区域,并以2011年3月11日发生在日本东北部海域的地震为例进行实验分析。
1 研究区与数据 1.1 研究区概况日本东北部地区濒临太平洋,该地区的山地与沿海平原相连接,为海浪高度的增加创造了条件。为降低海啸的影响,日本政府做了大量的设防工作,例如将居住区建设在高地、建立堤坝并且提前建设逃生公路。但是2011年3月11日的大地震还是造成了不可挽回的人员伤亡和难以估计的经济损失。
2011年3月11日日本东北太平洋海岸发生里氏9.0级特大地震,此次地震的测定震级是日本自1923年以来最高的一次,震源深度24km,日本多地震感明显,此次地震引发了大海啸,海啸波高达10m以上,造成2.8万人伤亡,并且大量的建筑物和村庄受到海啸影响而倒塌[10]。本文就以日本东北沿岸区域作为研究区域。
1.2 实验数据本文采用的SAR数据是2011年4月8日的ALOS PALSAR数据(图 1(a)),该数据为全极化模式,方位向分辨率为4.45m,距离向分辨率为23.14m。图 1(b)为震后高分辨率GeoEye-1光学图像,结合灾前高分辨率GeoEye-1图像选取4个不同损毁程度的损毁区域:区域1(R1)的损毁程度为80%~100%,区域2(R2)的损毁程度为50%~80%,区域3(R3)的损毁程度为20%~50%,区域4(R4)的损毁程度为0~20%,该结果与日本ZENRIN公司地面调查结果相一致;这4个不同损毁程度建筑物区域的位置如图 1(b)所示,细节图如图 1(c)所示。

|
Download:
|
| 图 1 试验区ALOS PALSAR图像及GeoEye-1图像 Fig. 1 ALOS PALSAR and GeoEye-1 images in test area | |
SAR特殊的成像方式以及建筑物复杂的几何结构和空间关系,导致建筑物SAR图像特征非常复杂,完全不同于光学图像和人类视觉特征,这增加了损毁建筑物认知和提取的难度。极化分解可以体现散射机制和散射特征的差异,通过不同散射机制的组合,可以从不同的方面体现不同损毁程度和未损毁建筑物的差异,进而实现损毁建筑物SAR图像的视觉优化和快速解译。因此,本文首先利用Yamaguchi分解和Touzi分解分析损毁建筑物的散射机制和特征,然后将显著散射特征进行组合,对灾后极化SAR图像进行视觉优化。
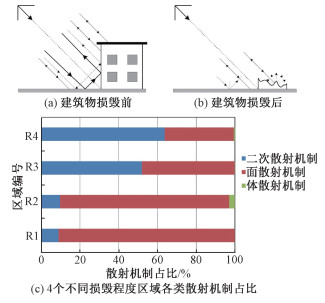
地面等表面与雷达信号交互产生的面散射机制、由于墙-地结构产生的二次散射机制以及由于三次反射形成的三次散射机制是完整的建筑物区域(地震前)主要的3种散射机制(如图 2(a)所示),其中建筑物区域占主导的散射机制是二次散射。但是当建筑物损毁时(如图 2(b)所示),建筑物的墙体坍塌,墙-地结构产生的二次散射遭到破坏,二次散射分量的占比减小,主导散射机制产生变化,此时,面散射的占比增加。并且建筑物损毁程度越严重,二次散射占比就会越小(如图 2(c)所示)。
|
Download:
|
| 图 2 建筑物区域损毁前后的散射机制 Fig. 2 Scattering mechanisms of building area pre-and post-damage | |
Yamaguchi分解和Touzi分解都属于非相干目标分解方法,在城市建筑物监测中具有广泛应用[10-12]。这两种极化分解方法得到的极化参数,尤其是Yamaguchi分解的二次散射分量和Touzi分解的散射角αs1,可以有效地反映散射机制,因此本文选择利用这两种极化分解方法对建筑物进行视觉优化和损毁评估。
2.1 Yamaguchi分解Yamaguchi等[13]在Freeman-Durden的基础上,考虑到城市里其他的反射不对称的情况,提出螺旋散射体分量,并将其作为第4个极化参量,该分量由螺旋体(等价于左旋或右旋圆极化状态)的散射引起,常常出现在城市区域,一般不存在于自然分布场中,该分量与城市区域建筑物的形状和结构息息相关。因此这种分解的方法对于建筑物结构和损毁的表述有一定的优势。Yamaguchi分解模型为
| $ \mathit{\boldsymbol{C}} = {f_{\rm{s}}}{\mathit{\boldsymbol{C}}_{\rm{s}}} + {f_{\rm{d}}}{\mathit{\boldsymbol{C}}_{\rm{d}}} + {f_{\rm{v}}}{\mathit{\boldsymbol{C}}_{\rm{v}}} + {f_{\rm{h}}}{\mathit{\boldsymbol{C}}_{\rm{h}}} $ | (1) |
式中:C为该像元的协方差矩阵;Cs、Cd、Cv、Ch分别为表面散射、二次散射、体散射和螺旋体散射协方差矩阵;fs、fd、fv、fh分别为表面散射、二次散射、体散射和螺旋体散射分解系数。通过Yamaguchi分解获得的各散射成分的功率以及总功率表达公式为:
| $ \left\{ \begin{array}{l} \;\;{P_{\rm{s}}} = {f_{\rm{s}}}(1 + {\left| \beta \right|^2}), \\ \;\;{P_{\rm{d}}} = {f_{\rm{d}}}(1 + {\left| \alpha \right|^2}), \\ \;\;\;\;\;\;{P_{\rm{v}}} = {f_{\rm{v}}}, \\ \;\;\;\;\;\;{P_{\rm{h}}} = {f_{\rm{h}}}, \\ P = {P_{\rm{s}}} + {P_{\rm{d}}} + {P_{\rm{v}}} + {P_{\rm{h}}}. \end{array} \right. $ | (2) |
式中:P代表总功率;Ps、Pd、Pv、Ph分别代表表面散射、二次散射、体散射和螺旋散射功率。
在基于模型的极化分解中一般会采用去定向处理[14-15],去定向实际上就是目标的定向角旋转的过程。极化SAR图像实际测量中的每一个像素点目标都有相应的定向角,为了消除这些随机分布的定向角,要将每个目标逆向旋转一个角度θ,使得目标都处于0°定向角的标准位置,再对后续的数据进行分析和处理,这个过程就是去定向的过程[16]。
在实际的观测中,目标定向角都是未知的,因此要先定义目标某种状态下的定向角为0°,然后再将目标旋转到这种状态下。目前通用的去定向定义为:目标通过围绕雷达视线,在与雷达视线垂直的平面上旋转,使得目标共极化通道(HH和VV)的能量达到最大[16]。
多视数据的定向角公式[10]为
| $ \theta = \frac{1}{4}\left( {{\rm{ta}}{{\rm{n}}^{ - 1}}\frac{{2{\rm{Re}}({T_{23}})}}{{{T_{22}} - {T_{33}}}} \pm n{\rm{ \mathsf{ π} }}} \right), n = 0, 1. $ | (3) |
对于多视数据T矩阵,由于只有T11和T22与共极化通道能量有关,而T11又不随定向角旋转而变化,因此去定向操作就是要通过定向角旋转使T22达到最大,并且使交叉极化功率T33达到最小。
二次散射机制、体散射机制以及表面散射机制是建筑物区域主要存在的3种散射机制,因此Yamaguchi分解是建筑物分析的常用极化分解方法,本文也利用未去定向和去定向的Yamaguchi分解进行建筑物损毁的评估分析。
2.2 Touzi分解Touzi分解是一种针对Cloude-Pottier分解对于特定散射机制散射类型的模糊性提出的一种旋转不变(roll-invariant)的非相干分解方法[17]。
Cloude-Pottier分解将相干矩阵T分解成独立的相干矩阵Tn之和[17-19]
| $ \mathit{\boldsymbol{T}} = \sum\limits_{i = 1}^3 {{\lambda _i}{\mathit{\boldsymbol{T}}_i}} . $ | (4) |
因此,每一个散射机制i(i=1, 2, 3)可以用秩为1的相干矩阵Ti和相应的标准正实部特征值λi/(λ1+λ2+λ3)来表示,并且可以用目标矢量ki来表示:
| $ {\mathit{\boldsymbol{T}}_i} = {\mathit{\boldsymbol{k}}_i} \cdot \mathit{\boldsymbol{k}}_i^{*{\rm{T}}}. $ | (5) |
其中*表示共轭,T表示向量转置。Cloude[18]指出,每一个目标矢量ki有一个等价的单次散射矩阵Si,ki可以用该矩阵中的元素来表示:
| $ {\mathit{\boldsymbol{k}}_i} = \frac{1}{{\sqrt 2 }}{\rm{ }}\left[ {{{({S_{{\rm{hh}}}})}_i} + {\rm{ }}{{({S_{{\rm{vv}}}})}_i}, {{({S_{{\rm{hh}}}})}_i} - {\rm{ }}{{({S_{{\rm{vv}}}})}_i}, 2{{({S_{{\rm{hh}}}})}_i}} \right]. $ | (6) |
Touzi分解也是基于相干矩阵T的特征分解,但与Cloude-Pottier不同的是,Touzi分解使用的是旋转不变的相干散射模型来参数化ki,并且可以得到4个旋转不变的参数[12]
| $ {\rm{ICT}}{{\rm{D}}_i} = {\rm{ }}({\alpha _{si}}, {\phi _{\alpha si}}, {\tau _i}, {\lambda _i}). $ | (7) |
Touzi分解一共产生12个参数,包括主要、中等和低散射分量(αsi, ϕαsi, τi, λi, i=1, 2, 3),复杂散射类型参数αs和ϕαs用来对对称目标散射机制提供明确描述,而τ代表目标散射对称度。其中每一个相干散射机制都可以用散射角αs、散射相位ϕαs和代表目标散射对称度的τ的极坐标轴来表示。归一化特征值λi表示每一个相应的特征向量i所代表的散射机制的相对能量。
对这12个参数进行分析发现,αs1、ϕαs1和|τ2|对建筑物区域比较敏感。其中,αs1反映区域的雷达信号与建筑物结构交互时产生的主要散射类型,完好建筑物区域以二次散射为主,而损毁建筑物区域因损毁程度的不同而存在不同的散射机制;主要散射相位ϕαs1提供的信息可以去除散射机制的模糊性;τ代表的是对称度,其中|τ2|在纯建筑物区域的值较小,趋于0,而在存在植被的建筑物区域的值较大,所以|τ2|可用于识别建筑物与植被的混合像元[12]。因此,我们选用Touzi分解的这3个参数进行建筑物损毁评估的分析实验。
2.3 极化散射特征选择和优化通过上面的分析发现,Yamaguchi分解的二次散射、体散射、表面散射,去定向后Yamaguchi分解的二次散射、体散射、表面散射以及Touzi分解的αs1、ϕαs1和|τ2|都对建筑物较为敏感,因此对这9个参数进行组合,分析验证哪3个参量进行组合时可以取得对建筑物损毁最佳的彩色合成和解译效果。分别以任意3个极化参量作为轴,绘制4个不同程度损毁区域的三维散点图,分析不同程度损毁区域的分散程度,图 3给出效果较好的3种组合。

|
Download:
|
| 图 3 4个不同损毁程度区域散点图比较 Fig. 3 Scatterplot comparison among four regions with different degrees of damage | |
可以看出,Yamaguchi分解的二次散射、体散射、表面散射的组合可以基本区分出不同损毁程度的区域,但是R1与R3重叠度较大,也就是说对损毁程度80%~100%和20%~50%之间的分辨能力较差,错分率较高,如图 3(a)所示;去定向后Yamaguchi分解的二次散射、体散射、表面散射的参数组合中,可以区分出损毁程度超过50%(R1,R2)与损毁程度小于50%(R3,R4)的建筑物区域,但是R1和R2基本全部重叠,也就是说损毁程度为50%~100%的建筑物无法区分,如图 3(b)所示;而Touzi分解的αs1、|τ2|、去定向的Yamaguchi分解的二次散射分量组合的效果最好,基本可以将R1、R2、R3和R4区分开,只在建筑物损毁程度小于20%时产生错分的情况,如图 3(c)所示。因此,可以利用这3种极化参量的组合进行灾后SAR图像的视觉效果优化和建筑物损毁评估。
3 实验结果与分析 3.1 Yamaguchi分解建筑物损毁评估在Yamguchi分解的合成图中,红色对应二次散射,绿色对应体散射,蓝色对应表面散射,如图 4所示。图中建筑区主要呈现亮粉红色,因为建筑区比较容易产生二面角反射,其散射以二次散射为主,而植被以体散射为主,主要表现为绿色。水体由于表面光滑,后向散射能量很少,因此呈现暗蓝色。未损毁区域和损毁轻微的区域如R4,在图像上呈现粉红色,而损毁的区域呈现蓝色和绿色,同时不同损毁级别的颜色也存在差异,损毁程度最严重的R1呈蓝色,R2呈绿色,R3呈粉色和黄色。但是将Yamaguchi分解得到的RGB合成图与GeoEye-1图像进行比较可以看出(图 3黄框细节图),Yamaguchi分解彩色合成图不能完全显示出所有建筑物区域,有很多建筑物目标被误分成植被,因此会影响建筑物损毁评估的效果。

|
Download:
|
| 图 4 Yamaguchi分解RGB合成图 Fig. 4 Yamaguchi decomposition RGB images | |
这是因为,当建筑物与雷达飞行器飞行路线不平行时,就会产生更多的体散射,二次散射会减少,因此,采用去定向后的Yamaguchi分解进行彩色合成,得到结果如图 5所示,其中,红色对应二次散射,绿色对应体散射,蓝色对应表面散射。与未去定向的Yamaguchi分解结果对比发现,检测到的建筑物区域的面积增大,大量与雷达飞行方向不平行的建筑物也呈现出来,与实际建筑物分布情况更加符合。但另一方面,在去定向后的Yamaguchi分解合成图上,损毁区域的视觉效果变差。R1、R2、R3、R4的损毁程度不同,但是除损毁程度较轻的R4外,另外3区域的显示效果基本没有差别,因此无法通过目视解译辨别不同的建筑物损毁程度。

|
Download:
|
| 图 5 去定向Yamaguchi分解RGB合成图 Fig. 5 Yamaguchi decomposition after deorientation RGB images | |
图 6、图 7分别为Touzi分解αs1分量、|τ2|分量。从图 6可以看出,在αs1分量图上,完好建筑物二次散射为主,αs1基本在80°~90°,所以在图像中呈现深红色(如R4);当建筑物损毁比较严重时(如R2、R3),该区域会混杂红色和绿色;当建筑物损毁非常严重时(如R1),该区域呈现蓝色。由图 7可以看出,建筑物区域的|τ2|值基本为0,可以很明显地与水体、植被区域分开;并且不同损毁程度的|τ2|的值也存在差异,这也有利于区分不同损毁程度的建筑物区域。当建筑物损毁程度较轻时(如R4、R3),其对应的|τ2|的值比较稳定,基本为0,所以在图像中呈现蓝色;但当建筑物损毁较为严重时(如R1、R2),其对应的|τ2|值波动较大,在图像中混杂红色和绿色。

|
Download:
|
| 图 6 Touzi分解的αs1分量 Fig. 6 αs1 of Touzi decomposition | |

|
Download:
|
| 图 7 Touzi分解的|τ2|分量 Fig. 7 |τ2|of Touzi decomposition | |
对以上各类极化目标分解分量的对比分析发现,去定向后的Yamaguchi分解的二次散射分量可以表征完好建筑区,而Touzi分解的αs1和|τ2|对建筑物的不同损毁程度非常敏感,这与图 3(c)得到最佳极化散射特征组合方案是一致的。
因此,利用去定向后的Yamaguchi分解得到的二次散射分量与Touzi分解得到的αs1和|τ2|进行RGB合成,红波段为Touzi分解的αs1分量,值越低表示损毁越严重;绿波段为去定向后的Yamaguchi分解的二次散射分量,值越低表示损毁越严重;蓝波段为Touzi分解的|τ2|分量,值越高且异质性越高表示损毁越严重。图 8为利用以上方案得到的彩色合成图,可以看到图像的视觉效果大大得以优化,建筑物区域与其他地物的对比得到增强,并且能够区分不同损毁程度的建筑物区域。图 8中,建筑物区域主要呈现为黄色,植被呈现为红色,水体呈现为蓝色;损毁最为严重的R1因为建筑物基本全部倒塌,只剩下裸露的平地,所以呈现为蓝色;R2损毁较为严重,部分位置呈现为蓝色,但还有完好的建筑物呈现黄色;R3轻微损毁,损毁区域呈现绿色;而R4基本没有损毁,建筑物完整,整个区域都呈现黄色。可见,利用本文方法优化后的RGB合成图不仅使得对建筑物的显示得到了改善,并且利用该视觉优化图还可以较容易地通过目视解译对不同损毁程度的建筑物区域进行区分。

|
Download:
|
| R: Touzi分解的αs1分量,G:去定向后的Yamaguchi分解二次散射分量,B: Touzi分解的|τ2|分量。 图 8 Yamaguchi分解与Touzi分解RGB合成图 Fig. 8 RGB image of Yamaguchi decomposition and Touzi decomposition | |
为验证该方法对于其他类型数据源的有效性,利用2008年5月12日汶川地震RADARSAT-2全极化数据进行验证实验,实验数据的具体参数如表 1所示。
|
|
表 1 汶川地震震后RADARSAT-2数据参数信息 Table 1 RADARSAT-2 data parameter information for Wenchuan earthquak |
该景图像主要覆盖四川省都江堰市,利用上述方法将Touzi分解得到的αs1、去定向后的Yamaguchi分解得到的二次散射分量和Touzi分解的|τ2|进行RGB合成,得到结果如图 9所示。在彩色合成图上,完好建筑物区域主要呈现为黄色,水体和裸地呈现为蓝色,植被呈现为蓝绿色。对照震前高分辨率光学图像可以看出,在该区域识别出两个损毁较为严重的区域R1和R2。R1为幸福镇,R2为聚源中学,两个区域的建筑物在地震中均遭受损毁,建筑物损毁后二面角结构减少,二次散射占比下降,面散射占比增加,因此,红波段Touzi分解的αs1分量值降低,绿波段去定向后的Yamaguchi分解二次散射分量值降低,而蓝波段Touzi分解的|τ2|分量增加,因而呈现为蓝色,与周边呈现为黄色的完好建筑物形成显著差别,可以容易地将损毁区域利用目视解译识别出来。证明本方法不仅适用于低分辨率的极化SAR数据,同样适用于高分辨率极化SAR数据。

|
Download:
|
| 图 9 RADARSAT-2全极化数据视觉优化图 Fig. 9 RADARSAT-2 full polarimetric data visual optimization image | |
本文针对完好建筑物和损毁建筑物目标的散射机制和特征,提出通过将去定向后Yamaguchi分解得到的二次散射分量、Touzi分解得到散射角αs1和对称度|τ2|这3个极化参量进行组合对灾后SAR图像进行视觉优化,进而对不同损毁程度建筑物区域进行解译和评估的方法,并且利用2011年3月11日日本大地震后的ALOS PALSAR数据进行实验和分析。结果表明,该方法可以有效优化SAR图像的视觉效果,使得建筑物目标更容易识别,并且可以区分不同损毁程度的建筑物区域,因此可以实现利用单时相极化SAR图像对建筑物损毁进行评估,大大降低了传统方法对多时相SAR数据的需求,有利于提高灾害应急监测的时效性。
| [1] |
Hao H M, Zhang Y H, Shi H Y. Application of test statistic method in fully polarimtric SAR change detection[J]. Journal of Remote Sensing, 2012, 16(3): 520-532. |
| [2] |
Shen J C, Xu X, Dong H, et al. Collapsed building extraction from single full polarimetric SAR image after earthquake[J]. Science Technology and Engineering, 2015, 15(14): 86-91. |
| [3] |
王庆.基于极化SAR的建筑物震害信息提取研究[D].北京: 北京大学, 2014.
|
| [4] |
闫丽丽.基于散射特征的极化SAR影像建筑物提取研究[D].北京: 中国矿业大学(北京), 2013.
|
| [5] |
孙萍.极化SAR图像建筑物提取方法研究[D].北京: 首都师范大学, 2013.
|
| [6] |
Wang X Q, Jin D J, Dou A. Study on the fractal analysis of SAR images and its application to the extraction of seismic damage of 2010 Yushu, China Ms=7.1 earthquake[C]//Sato M. Geoscience and Remote Sensing. Vancouver: IEEE, 2011: 1981-1984.
|
| [7] |
Guo H D, Li X W, Zhang L. Study of detecting method with advanced airborne and spaceborne synthetic aperture radar data for collapsed urban buildings from the Wenchuan earthquake[J]. Journal of Applied Remote Sensing, 2009, 3(1): 131-136. |
| [8] |
Li X W, Guo H D, Zhang L, et al. A new approach to collapsed building extraction using RADARSAT-2 polarimetric SAR imagery[J]. IEEE Geoscience & Remote Sensing Letters, 2012, 9(4): 677-681. |
| [9] |
Zhang H Z, Wang Q, Zeng Q M, et al. A novel approach to building collapse detection from post-seismic polarimetric SAR imagery by using optimization of polarimetric contrast enhancement[C]//2015 IEEE International Geoscience and Remote Sensing Symposium. Milan: IEEE, 2015, 3270-3273.
|
| [10] |
Chen S W, Sato M. Tsunami damage investigation of built-up areas using multitemporal spaceborne full polarimetric SAR images[J]. IEEE Transactions on Geoscience & Remote Sensing, 2013, 51(4): 1985-1997. |
| [11] |
Sato M, Chen S W, Satake M. Polarimetric SAR analysis of tsunami damage following the March 11, 2011 East Japan earthquake[J]. Proceedings of the IEEE, 2012, 100(10): 2861-2875. Doi:10.1109/JPROC.2012.2200649 |
| [12] |
Bhattacharya A, Touzi R. Polarimetric SAR urban classification using the Touzi target scattering decomposition[J]. Canadian Journal of Remote Sensing, 2012, 37(4): 323-332. |
| [13] |
Yamaguchi Y, Moriyama T, Ishido M, et al. Four-component scattering model for polarimetric SAR image decomposition[J]. IEEE Transactions on Geoscience & Remote Sensing, 2005, 43(8): 1699-1706. |
| [14] |
An W, Yi C, Jian Y. Three-component model-based decomposition for polarimetric SAR data[J]. IEEE Transactions on Geoscience & Remote Sensing, 2010, 48(6): 2732-2739. |
| [15] |
Yamaguchi Y, Sato A, Boerner W M, et al. Four-component scattering power decomposition with rotation of coherency matrix[J]. IEEE Transactions on Geoscience & Remote Sensing, 2010, 49(6): 2251-2258. |
| [16] |
安文韬.基于极化SAR的目标极化分解与散射特征提取研究[D].北京: 清华大学, 2010.
|
| [17] |
Touzi R. Target scattering decomposition in terms of roll-invariant target parameters[J]. IEEE Transactions on Geoscience & Remote Sensing, 2006, 45(1): 73-84. |
| [18] |
Cloude S R. Group theory and polarisation algebra[J]. Optik, 1986, 75: 26-36. |
| [19] |
Li K, Shao Y, Touzi R, et al. Rice monitoring using touzi decomposition based on polarimetric SAR data in Southwestern China[C]//Brisco B. Progress in Electromagnetics Research Symposium. Suzhou: The Electromagnetics Academy, 2011: 827-830.
|
 2020, Vol. 37
2020, Vol. 37 


