随着科学技术的进步和工业的发展，有毒有害气体的使用范围在不断扩大。这些气体既可能是生产之初需要的原材料，比如大多数的有机化学物质，也可能是生产过程中各个环节产生的副产品，比如一氧化碳、氨、硫化氢等等。有害气体影响人类的身体健康，所以有害气体的检测在我们的生产和生活中十分重要。

在检测气体的过程中用到的最关键的元器件就是气体传感器，气体传感器是一种能够感知外部环境中某种气体及其浓度变化的气体敏感元器件。针对不同检测任务，例如气体浓度预测(回归)^[1-2]，气体识别(分类)^[3]，类似气体的分组(聚类)^[4]，实验人员会使用气体传感器阵列设计不同的实验^[5]。本文主要关注气体浓度预测(回归)，实验中获得的气体传感器阵列的多变量响应都携带着有关气体浓度变化的信息^[6]，可以通过传感器的响应分析混合气体的种类和浓度。

为预测气体浓度，首先有必要建立一个联系气体传感器响应与真实气体浓度的校准模型。传统的方法是建立一些特定的参数模型，包括线性的或者非线性的^[7]。比如，文献[2, 5]使用线性模型对气体传感器数据进行定量的多元分析；文献[8-9]根据实验经验提出使用幂函数模型来刻画气体传感器的相对导电率与气体浓度变化之间的关系；文献[10]经过理论上的考虑提出另一种形式的参数模型；文献[11]则提出使用对数模型建立传感器与气体浓度之间的联系。尽管这些文献提出的模型都是联系气体传感器响应与气体浓度之间关系的，但是它们彼此之间还是存在着一定的差异。在实际应用中，真实模型的形式会因为气体种类和传感器类型的不同而不同。因此，如果选错了对应的模型，可能会导致最后无法得到较好的预测结果。

为了避免模型设定的错误，本文采用非参数模型建立每个传感器与气体浓度之间的联系。采用局部线性核回归的方法对非参数模型进行拟合。对于每个非参数模型中的窗宽参数，采用交叉验证的方法进行选取。在得到非参数模型拟合结果的同时，还可以得到非参数模型函数关于气体浓度这个协变量一阶偏导数的估计。这个一阶偏导数的估计在后面对气体浓度进行逆向预测的时候会起到很大的作用。

这里使用非参数模型建模，主要是考虑到非参数模型本质上包括线性模型与非线性模型这些特殊情况。采用非参数模型进行建模也降低了由于模型选择错误带来的气体浓度预测误差较大的风险，具有弱假设条件的非参数模型在面对数据污染的情况时会表现得更加稳健^[12]。

紧接着，需要对气体的浓度进行预测。这里面临的预测问题与传统的预测问题不同，传统的预测问题往往是在已知协变量的情况下预测响应变量的值。但在实际情况中，只能观察到气体传感器的响应，也即回归模型中的因变量。然后利用前面拟合好的模型，在已知气体传感器响应的情况下，逆向预测气体的浓度。为了得到更精确的预测结果，在实验过程中，往往会使用比混合气体种类更多的气体传感器，这样会得到比气体浓度更多的气体传感器数据。通过代入已经拟合好的非参数模型，建立多个新的气体传感器响应与未知浓度气体之间的联系，最小化它们之间的误差，得到未知气体浓度的预测值^[13]。在后面的数值模拟分析和实际数据分析的过程中，我们发现非参数模型的表现都好于特定的参数模型。

1 模型与求解

在使用传感器进行实验的过程中，可以观察到{y_1 t, …, y_mt; x_1 t, …, x_kt}_t=1ⁿ，其中{y_1 t, …, y_mt}_t=1ⁿ表示m个传感器的响应读数，{x_1 t, …, x_kt}_t=1ⁿ表示k种气体的真实浓度。但是，在真实环境中，得到的仅仅是m个传感器的响应读数。因此，我们的目标是通过已知的m个传感器的响应读数逆向预测k种气体的真实浓度。

为避免模型假定的错误，首先使用非参数模型对气体传感器响应与真实的气体浓度之间的关系进行建模，模型如下所示：

$ {y_{it}} = {f_i}({\mathit{\boldsymbol{X}}_t}) + {\epsilon_{it}},t = 1, \cdots ,n,i = 1, \cdots ,m, $

(1)

式中：y_it表示第i个传感器的第t次观察值，X_t=(x_1 t, …, x_kt)^T表示第t次观察时对应的k种气体浓度，$ {{\boldsymbol{\epsilon }}_{it}}$表示随机误差。这里假定误差是独立同分布的，且均值为0。同时假定x_jt, j=1, …, k这些协变量有紧凑的支撑Ω=[0, 1]。在实际应用中，如果x_jt ∉[0, 1]，需要对所有的协变量进行归一标准化，如下所示

$ \frac{{{x_{jt}} - {\rm{mi}}{{\rm{n}}_{t = 1, \cdots ,n}}({x_{jt}})}}{{{\rm{ma}}{{\rm{x}}_{t = 1, \cdots ,n}}({x_{jt}}) - {\rm{mi}}{{\rm{n}}_{t = 1, \cdots ,n}}({x_{jt}})}}, $

(2)

式中：$ \mathop {{\rm{min}}}\limits_{t = 1, \cdots , n} ({x_{jt}})$和$\mathop {{\rm{max}}}\limits_{t = 1, \cdots , n} ({x_{jt}}) $分别表示n次观察中第j种气体的最小和最大浓度。接下来需要通过局部线性核回归的估计方法来拟合f_i(·)^[14-15]。对于未知的气体浓度x=(x₁, x₂, …, x_k)^T，可以同时得到f_i(x)的估计和f_i(x)关于气体浓度x一阶偏导β_i(x)的估计。其中一阶偏导β_i(x)的估计对后面进行气体浓度的逆向预测会起到很大的作用。模型f_i(·)及其偏导的估计如下：

$ {({\hat f_i}(\mathit{\boldsymbol{x}}),{\hat \beta _i}{(\mathit{\boldsymbol{x}})^{\rm{T}}})^{\rm{T}}} = {(\mathit{\boldsymbol{X}}_x^{\rm{T}}{\mathit{\boldsymbol{W}}_{{x_i}}}{\mathit{\boldsymbol{X}}_x})^{ - 1}}(\mathit{\boldsymbol{X}}_x^{\rm{T}}{\mathit{\boldsymbol{W}}_{{x_i}}}{\mathit{\boldsymbol{Y}}_i}), $

(3)

式中：Y_i=(y_i1, …, y_in)^T, W_xi=diag{K_hi(X₁-x), …, K_hi(X_n-x)},

$ {\mathit{\boldsymbol{X}}_x} = \left( {\begin{array}{*{20}{c}} 1&{{{({\mathit{\boldsymbol{X}}_1} - \mathit{\boldsymbol{x}})}^{\rm{T}}}}\\ \vdots & \vdots \\ 1&{{{({\mathit{\boldsymbol{X}}_n} - \mathit{\boldsymbol{x}})}^{\rm{T}}}} \end{array}} \right), $

$ {K_{{h_i}}}(\mathit{\boldsymbol{x}}) = {({h_{{i_1}}}{h_{{i_2}}} \cdots {h_{{i_k}}})^{ - 1}}\prod\limits_{j = 1}^k {g({x_j} \cdot h_{{i_j}}^{ - 1})} $，g(·)是核函数，h_i=(h_i1, h_i2, …, h_ik)^T为窗宽参数。

通过上面的处理，对每个气体传感器与气体浓度之间的非参数模型进行了拟合。因为我们的目的是预测未知的气体浓度，所以需要根据拟合好的非参数模型，对k种气体浓度进行逆向预测。

假设观察到m个新的传感器的响应为Y_new=(y_new1, …, y_newm)^T，需要预测未知的k种气体浓度记为X_new=(x_new1, …, x_newk)^T。根据前面提出的非参数模型(1)，可以得到如下等式

$ \begin{array}{*{20}{c}} {{y_{{\rm{ne}}{{\rm{w}}_{\rm{1}}}}} = {f_1}({\boldsymbol{X}_{{\rm{new}}}}) + {\epsilon_1},}\\ \vdots \\ {{y_{{\rm{ne}}{{\rm{w}}_m}}} = {f_m}({\boldsymbol{X}_{{\rm{new}}}}) + {\epsilon_m}.} \end{array} $

其中$ \boldsymbol{\epsilon} ={{({{\boldsymbol{\epsilon} }_{1}}, \cdots , {{\boldsymbol{\epsilon} }_{m}})}^{\text{T}}}$表示随机误差。

接下来，采用最小二乘法得到未知浓度的气体的逆向预测值。通过代入拟合好的m个传感器对应的非参数模型，需要最小化如下残差平方和

$ S({\mathit{\boldsymbol{X}}_{{\rm{ new }}}}) = \sum\limits_{i = 1}^m {({y_{{\rm{ new}}{{\rm{ }}_i}}} - {{\hat f}_i}(} {\mathit{\boldsymbol{X}}_{{\rm{ new }}}}){)^2}. $

(4)

将式(4)的极小值当做是X_new的逆向预测值。这里采用高斯牛顿法来求极小值^[16]。前面介绍的非参数模型f_i(·)关于气体浓度的偏导数估计在这里发挥了关键的作用，下面介绍如何应用高斯牛顿法解决非参数模型下气体浓度的逆向预测问题。

首先需要给未知的气体浓度设定一个初始值，记为X₀，然后将非参数模型$ {{{\hat{f}}}_{i}}$(·)在X₀这点做一阶泰勒展开，那么残差平方和S(X_new)的表达式约等于如下形式

$ \sum\limits_{i = 1}^m {{{[{y_{{\rm{ new}}{{\rm{ }}_i}}} - \{ {{\hat f}_i}({\mathit{\boldsymbol{X}}_0}) + {{({\mathit{\boldsymbol{X}}_{{\rm{ new }}}} - {\mathit{\boldsymbol{X}}_0})}^{\rm{T}}}{{\mathit{\boldsymbol{\hat \beta }}}_i}({\mathit{\boldsymbol{X}}_0})\} ]}^2}} . $

(5)

对式(5)进行简单的改写，再使用普通最小二乘法可以得到X_new的首次更新值，记为X₀⁽¹⁾，具体表达式如下

$ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{X}}_0^{(1)} = {\mathit{\boldsymbol{X}}_0} + {{(\mathit{\boldsymbol{\hat \beta }}{{({X_0})}^{\rm{T}}}\mathit{\boldsymbol{\hat \beta }}({\mathit{\boldsymbol{X}}_0}))}^{ - 1}}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \{ \mathit{\boldsymbol{\hat \beta }}{{({\mathit{\boldsymbol{X}}_0})}^{\rm{T}}}({\mathit{\boldsymbol{Y}}_{{\rm{new}}}} - \mathit{\boldsymbol{\hat f}}({\mathit{\boldsymbol{X}}_0}))\} .} \end{array} $

(6)

其中$\mathit{\boldsymbol{\hat f}}({\mathit{\boldsymbol{X}}_0}) = {\left( {{{\hat f}_1}({\mathit{\boldsymbol{X}}_0}), \cdots ,{{\hat f}_m}({\mathit{\boldsymbol{X}}_0})} \right)^{\rm{T}}},\mathit{\boldsymbol{\hat \beta }}({\mathit{\boldsymbol{X}}_0}) = {\left( {\mathit{\boldsymbol{\hat \beta }}_1^{\rm{T}}({\mathit{\boldsymbol{X}}_0}), \ldots ,\mathit{\boldsymbol{\hat \beta }}_m^{\rm{T}}({\mathit{\boldsymbol{X}}_0})} \right)^{\rm{T}}}$.

然后判断‖X₀⁽¹⁾-X₀‖ < ε是否成立，其中ε是一个很小的数, 本文令ε=10^-3。如果不成立，需要把第一次更新的值X₀⁽¹⁾赋给X₀，然后通过迭代式(6)得到X₀⁽²⁾。不断重复上面的步骤，直到‖X₀^(q)-X₀^(q-1)‖ < ε, 就得到最终的估计，其中X₀^(q)表示第q次迭代的结果。最终将X₀^(q)当做浓度未知气体X_new的预测值，记为${{\mathit{\boldsymbol{\hat X}}}_{{\rm{new}}}} $。

如果前面对协变量进行了归一化处理，则还需要进行逆归一化的操作才能得到气体的逆向预测值${{\mathit{\boldsymbol{\hat X}}}_{{\rm{new}}}} $，具体步骤如下

$ {\hat x_{{\rm{ new}}{{\rm{ }}_j}}} = x_{{0_j}}^{(q)}(\mathop {{\rm{max}}}\limits_{t = 1, \cdots ,n} ({x_{jt}}) - \mathop {{\rm{min}}}\limits_{t = 1, \cdots ,n} ({x_{jt}})) + \mathop {{\rm{min}}}\limits_{t = 1, \cdots ,n} ({x_{jt}}), $

(7)

其中$ {{\hat x}_{{\rm{ne}}{{\rm{w}}_j}}}$是${{\mathit{\boldsymbol{\hat X}}}_{{\rm{new}}}} $的第j项值，x_0j^(q)是X₀^(q)的第j项值。

2 窗宽选择

在前面介绍的基于非参数模型对气体浓度进行逆向预测的方法中，首先是对每个传感器对应的非参数模型进行拟合，当时采用的拟合方法是局部线性核回归。采用核方法比较关键的一步是确定核函数的窗宽。为了使得下一步能够更好地对气体浓度进行预测，需要根据已有的数据提高非参数模型的拟合精度，因此需要尽量减小第一步所产生的拟合误差。下面介绍本文采用的窗宽选择方法。

关于非参数模型窗宽选择的方法，很多文献有过讨论。比如，文献[17]证明在具有单个连续协变量的回归模型中，在使用局部多项式方法拟合时，通过交叉验证选择得到的带宽具有渐近最优性。文献[18-19]指出利用数据驱动选择窗宽的方法在非参数模型设定的情形下应用十分广泛，并证明在具有多个协变量的非参数模型中，通过交叉验证选择得到的窗宽在代入模型之后的渐进正态性。以上研究都表明在非参数模型设置下使用交叉验证进行窗宽选择具有良好的表现，因此这里也采用交叉验证的方法进行窗宽选择。下面需要最小化交叉验证(CV)得分，表达式为

$ CV({h_{{i_1}}}, \cdots ,{h_{{i_k}}}) = \frac{1}{n}\sum\limits_{t = 1}^n {({y_{it}} - \hat f_i^{( - t)}(} {\mathit{\boldsymbol{X}}_t}){)^2}, $

(8)

式中$ \hat f_i^{\left( { - t} \right)}$(X_t)表示去除第t次观察(X_t^T, y_it)之后得到的f_i(X_t)的留一估计。

在实际应用中，如果直接最小化式(8)来选择窗宽，需要进行n次非参数模型的拟合，计算成本很大。文献[20]指出CV(h_i1, …, h_ik)可以进一步简化为

$ CV({h_{{i_1}}}, \cdots ,{h_{{i_k}}}) = \frac{1}{n}\sum\limits_{t = 1}^n {\frac{{{{({y_{it}} - {{\hat f}_i}({\mathit{\boldsymbol{X}}_t}))}^2}}}{{{{(1 - {\mathit{\boldsymbol{S}}_{{h_i}}}(t,t))}^2}}}} , $

(9)

其中S_hi表示局部线性光滑矩阵，定义如下

$ {\mathit{\boldsymbol{S}}_{{h_i}}} = \left( {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{e}}_1^{\rm{T}} \cdot {\mathit{\boldsymbol{S}}_{{d_i}}}({\mathit{\boldsymbol{X}}_1})}\\ \vdots \\ {\mathit{\boldsymbol{e}}_1^{\rm{T}} \cdot {\mathit{\boldsymbol{S}}_{{d_i}}}({\mathit{\boldsymbol{X}}_n})} \end{array}} \right), $

式中：S_di(x)=(X_x^TW_xiX_x)^-1(X_x^TW_xi)，e_i=(0, …, 1, …, 0)^T是一个长度为(k+1)的单位列向量，其中除第i个元素为1其余都为0。

显而易见，最小化式(9)比最小化式(8)节省很大的计算量。因此我们将通过最小化式(9)来选择${{\hat f}_i} $(x)的窗宽。

3 数值模拟

本节将通过数值模拟检验基于非参数模型的气体浓度逆向预测方法的效果。首先介绍一下以前的学者提出的一些描述气体传感器响应与气体浓度之间关系的校准模型。Clifford和Tuma^[8-9]根据实验观察，提出将传感器相对电导率与气体浓度联系起来的经验公式。该模型可以通过幂函数来描述，表达式如下

$ {y_{{\rm{ pow }}}}(x) = {(1 + b \cdot x)^\beta }, $

(10)

式中：y_pow(x)=G₀/G_g(x)表示传感器的相对导电率，G₀表示传感器在空气中的基础导电率，G_g(x)表示传感器在气体浓度为x下的导电率，b和β是未知的参数。

除此之外，Chaiyboun等^[11]提出拟合传感器响应的对数模型，表达式如下

$ {y_{{\rm{log}}}}(x) = a - b \cdot {\rm{ln}}(x + 0.5), $

(11)

式中：a和b为未知的模型参数，x表示气体浓度。

与此同时，Chaiyboun等^[11]将式(10)和式(11)都推广到两种混合气体的情形，表达式如下

$ \begin{array}{*{20}{l}} {{y_{{\rm{ pow }}}}({x_1},{x_2}) = }\\ {{{\left( {1 + {b_1} \cdot \left[ {{x_1} + \frac{{{{\{ {{(1 + {b_2} \cdot {x_2})}^{{\beta _2}}}\} }^{1/{\beta _1}}}}}{{{b_1}}}} \right]} \right)}^{{\beta _1}}},} \end{array} $

(12)

式中：b₁, β₁, b₂, β₂为未知的模型参数；x₁, x₂分别表示两种混合气体各自的气体浓度。

$ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {y_{{\rm{log}}}}({x_1},{x_2}) = {a_0} - {b_0} \cdot \\ {\rm{ln}}\left( {{x_1} + {\rm{exp}}\left[ {\frac{{{a_0} - \{ {a_1} - {b_1} \cdot {\rm{ln}}({x_2} + 0.5)\} }}{{{b_0}}}} \right]} \right), \end{array} $

(13)

式中：a₀, b₀, a₁, b₁为对数模型的参数；x₁, x₂分别表示两种混合气体各自的气体浓度。

接下来，使用Clifford和Tuma^[8-9]提出的幂函数模型生成模拟数据。然后分别使用对数模型、幂函数模型和非参数模型构建校准模型。通过给定新的传感器阵列响应，使用这些拟合好的模型对气体浓度进行逆向预测，并比较它们的表现。下面分别考虑单一气体和两种混合气体的情况。

3.1 单一气体

这里假设有单一气体和8个半导体气体传感器，气体浓度由范围为[0, 500]的均匀分布产生。不同传感器的幂函数模型(10)的预定义系数如表 1所示。每次模拟生成的样本数为1000。

根据式(10)产生对应的模拟数据，具体地，对于气体浓度x_j，第k个传感器的响应可以根据下面这个表达式产生：

$ {y_{kj}} = {y_{{\rm{ pow }}}}({x_j}) + \sigma {\boldsymbol{\epsilon}_{kj}}, $

(14)

式中：$ {{\boldsymbol{\epsilon} }_{kj}}$为独立同分布的标准正态随机变量，k=1, …, 8, j=1, …, 1000。误差的方差σ²根据信躁比的大小来确定，信噪比(SNR)的定义为y_pow(x₁), …, y_pow(x₁₀₀₀)的样本方差与误差${{\boldsymbol{\epsilon} }_{1}} $, …, ${{\boldsymbol{\epsilon} }_{1000}} $的样本方差的比值。我们分别考虑SNR=4和SNR=8这两种情况。

根据6:4的比例将生成的数据分成两个部分，其中60%的数据进行训练，40%用于测试。接下来，通过对训练数据集进行交叉验证来确定不同传感器对应的非参数模型(1)的窗宽参数。然后使用非参数模型对单一气体的浓度进行逆向预测。本文采用高斯核作为加权函数。同样，首先使用训练数据拟合对数模型(11)和幂函数模型(10)。紧接着根据拟合好的8个传感器对应的对数模型和幂函数模型，通过非线性最小二乘的方法，对气体浓度进行逆向预测。

分别在训练集和测试集上使用3种不同的模型对气体浓度进行逆向预测。为评估最终预测结果的好坏，通过计算预测气体浓度与真实气体浓度之间的根均方误差(RMSE)来衡量，表达式为RMSE= $\sqrt {\left( {1/n} \right)\sum _{i = 1}^n{{({x_i} - {{\hat x}_i})}^2}} $，其中x_i是气体浓度的真实值，${{{\hat x}_i}} $为气体浓度的预测值。

最后，将上述模拟过程重复200次，并计算200次模拟结果的RMSE的均值和标准差(SD)。同时使用对数模型(11)、幂函数模型(10)和非参数模型(1)对气体浓度进行逆向预测，结果汇总在表 2中。

从表 2可以看出，使用对数模型对气体浓度进行逆向预测的效果不如幂函数模型和非参数模型。同时可发现使用非参数模型对气体浓度进行逆向预测能够取得与正确模型幂函数模型相同的效果，且使用这两种模型得到的RMSE的标准差相比对数模型也是比较小的。

3.2 混合气体

这一部分，考虑存在两种混合气体和8个半导体气体传感器的情况。每种气体浓度同样由范围为[0, 500]的均匀分布产生。表 3列出8个不同传感器对应的幂函数模型(12)的预定义系数。每次模拟生成的样本数为1000。

因此采用适合两种气体状况的模型(12)产生数据，对于给定的气体浓度x_1j和x_2j，第k个传感器的响应由如下表达式产生：

$ {y_{kj}} = {y_{{\rm{ pow }}}}({x_{1j}},{x_{2j}}) + \sigma {\boldsymbol{\epsilon}_{kj}}, $

(15)

式中：$ {{\boldsymbol{\epsilon} }_{kj}}$是服从独立同分布的标准正态的随机变量，k=1, …, 8, j=1, …, 1000。噪音的方差σ²同样由SNR来确定。这里也考虑SNR=4和SNR=8两种情况。

同样地，将数据分成60%的训练集和40%的测试集。运用对数模型(13)、幂函数模型(12)和非参数模型(1)在训练集和测试集上分别对气体浓度进行逆向预测，然后通过计算气体的预测浓度与真实浓度之间的RMSE比较这3种模型的表现。整个模拟过程重复200次。接下来对比对数模型(13)、幂函数模型(12)和非参数模型(1)在两个数据集上的表现，结果如表 4所示。

正如从表 4中看到的，对于两种气体的情况，采用非参数模型对气体浓度进行逆向预测的结果也好于对数模型。同时，非参数模型同样也达到了与使用正确模型幂函数模型一样的效果。其中幂函数模型和非参数模型对应的RMSE的标准差都是比较小的，因此可以认为非参数模型体现了更加稳定的逆向预测能力。

4 实际数据分析

这一节主要是通过对实际的气体传感器数据进行分析，对比对数模型、幂函数模型和非参数模型对气体浓度逆向预测的表现。本文使用Fonollosa等^[21]在UCI机器学习网站上分享的气体传感器数据。这个数据集记录了浓度变化的混合气体暴露在16个气体传感器的环境下，气体浓度与传感器响应的时间序列数据。其中作者分别对两种混合气体的组合进行了实验，一种为乙烯与甲烷在空气中的组合，另一种为乙烯和一氧化碳在空气中的组合。每组实验持续12h，不断改变混合气体的浓度，分别记录16个气体传感器的读数。这16个传感器包含4种类型：TGS-2602，TGS-2600，TGS-2610，TGS-2620，其中每种传感器有4个。实验中气体的浓度每间隔80~120s会随机改变一次，其中乙烯的浓度变化范围为(0~20)×10^-6，一氧化碳浓度的变化范围为(0~600)×10^-6，甲烷浓度的变化范围为(0~300)×10^-6。

首先，分析乙烯和一氧化碳这个气体组合。为了更好地了解气体传感器数据，随机截取一段时间的传感器数据，按照气体传感器的种类分组展示传感器读数的变化，如图 1所示。

图 1依次展示TGS-2602，TGS-2600，TGS-2610，TGS-2620这4种类型的传感器的读数。发现TGS-2602传感器在某些时刻会产生突变，无法对气体浓度变化做出规律的反应。因此，在后面的分析步骤中，会去掉这个传感器的数据。同时，Fonollosa等^[21]在网站上提供的气体浓度数据是设定时刻的浓度值，而我们在模型中考虑的是传感器响应与气体真实浓度之间的关系。因此需要考虑设定时刻的气体浓度到达传感器过程中的时间延迟。根据Fonollosa等^[21]的数据处理代码，得到气体到达传感器的不同时间，一氧化碳和甲烷为17.82s，乙烯为26.73s。为了将真实的气体浓度与传感器的读数进行匹配，需要根据前面计算出来的延迟时间对气体浓度数据进行平移。例如：在t秒时的一氧化碳的实际浓度需用(t-17.82)s处的设定浓度值代替，乙烯在t秒时的实际浓度需用(t-26.73) s处的设定浓度值代替。

为对比气体浓度平移变换前后的不同，分别画出未经平移变换和经过平移变换后的乙烯和一氧化碳的浓度与气体传感器阵列的读数变化图，如图 2和图 3所示。图 2为未经平移处理的情况，第1个面板图展示15个传感器的读数变化，垂直虚线标示对应的浓度变化时刻，第2和第3个面板图展示未经平移变换的乙烯和一氧化碳浓度的变化。图 3为经过平移处理的情况，第1个面板图展示15个传感器的读数变化，垂直虚线标示对应的浓度变化时刻，第2和第3个面板图展示经过平移变换的乙烯和一氧化碳浓度的变化。

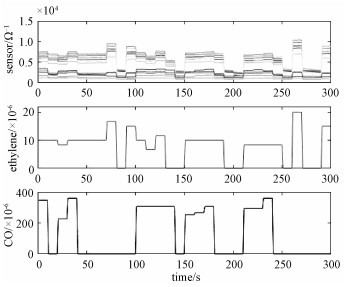
通过图 2和图 3的对比，发现经过平移处理后传感器读数的变化与气体浓度的变化更为一致，因此在分析数据之前需要对气体的浓度数据进行平移。同时，从图 3可以看出，在气体浓度转换的阶段，传感器的读数都会发生突变，但这段突变并不能显示传感器与对应气体浓度的关系。因此后面的分析过程中，去掉了这些突变的部分，处理之后的数据如图 4所示。

采用对数模型(13)、幂函数模型(12)和非参数模型(1)对气体浓度进行逆向预测，其中对数模型和幂函数模型的响应变量是传感器的相对导电率。而Fonollosa等^[21]给出的传感器读数为其导电率，需要对原始数据进行处理得到相对导电率。而我们提出的非参数模型对响应变量的具体含义并没限制。

在使用非参数模型(1)时分别考虑两种不同的情况：第1种情况考虑模型(1)的响应变量y为相对导电率；第2种情况考虑模型(1)的响应变量y为作者给定的原始读数。然后比较使用对数模型(11)、幂函数模型(10)和非参数模型(1)进行气体浓度逆向预测的表现，结果如表 5所示。括号中的RC表示模型因变量使用的是传感器的相对导电率，OR表示模型因变量使用的是传感器的原始读数。

根据同样的步骤分析甲烷和乙烯这个气体组合的数据，结果如表 6所示。

从表 5和表 6的结果可以看出非参数模型的表现优于对数模型和幂函数模型。进一步发现直接使用传感器的原始读数建立模型，得到的RMSE更小。通过实际分析结果可以看出使用非参数模型对气体浓度进行逆向预测具有更高的灵活性，同时也可以得到比非线性模型更好的预测结果。

5 结论与展望

本文提出一种基于非参数模型的气体浓度的逆向预测方法，通过数值模拟和实际数据分析两个维度对比非参数模型、对数模型和幂函数模型的表现。从数值模拟的结果可以看出，当模型选择错误时，对数模型的结果不如非参数模型和正确的幂函数模型，同时在使用非参数模型对气体浓度进行逆向预测时也取得了与幂函数模型一样好的结果。实际分析结果也表明非参数模型对气体浓度进行逆向预测的效果好于对数模型和幂函数模型。

在构建传感器响应与气体浓度之间关系的过程中，一些学者提出的线性模型和非线性模型过于具体。在实际应用中，如果假定的模型与实际的模型有偏差，气体的预测结果将会受到影响。因此，我们建议采用非参数模型构建校准模型。

在对气体浓度进行逆向预测的步骤中，需要采用高斯牛顿法最小化传感器响应与模型之间的误差。高斯牛顿法以前一般是应用于非线性的最小二乘问题，而我们在使用非参数模型建模对气体浓度进行逆向预测时，需要解决的是非参数的最小二乘问题。由于在使用局部线性核回归方法拟合非参数模型时，也得到了非参数模型关于自变量偏导数的估计，这里创造性地将这个偏导数应用到高斯牛顿法中，也解决了非参数的最小二乘问题。

虽然本文提出的方法是应用于气体浓度的预测问题，但是它对解决生物学和药学等其他领域的一些问题也具有一定的借鉴意义。例如，当遇到只能观察到响应变量、但是感兴趣的协变量和两者之间的关系都未知的情况时，就可以使用基于非参数模型对协变量进行逆向预测的方法。

在实际应用这些方法的过程中，我们发现非参数模型进行运算需要的时间多于非线性的参数模型。主要有如下两个原因：一方面，使用式(3)拟合非参数模型需要复杂的计算；另一方面，在使用非参数回归进行逆向预测步骤中，重复迭代式(6)会增加计算负担。这也是使用非参数模型进行逆向预测方法的缺陷之一。此外，在拟合非参数模型的步骤中，认为误差是独立同分布的。可以进一步研究相关误差的情况，最终的预测准确率可能会有所改善。