2. 中国科学院大学, 北京 100049;
3. 中国科学院上海微系统与信息技术研究所, 上海 200050
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Shanghai Institute of Microsystem and Information Technology, Chinese Academy of Sciences, Shanghai 200050, China
乳腺癌是妇女所患癌症中发病率最高、死亡率第二高的癌症,对世界各地妇女的健康构成了巨大威胁[1]。虽然临床治疗技术,如放疗、化疗等是当前普遍采用的方案,但它们在效率、副作用、成本和侵害性等方面有着明显的局限性。热疗法作为可替代方案,是指使用加热(包括微波、射频、高强度聚焦超声)治疗癌症,正成为越来越多的实验室和临床研究的重点[2-3]。无论是电磁波或超声波产生的温度上升(通常高于50 ℃),都会非常迅速地导致局部肿瘤组织的破坏。临床上已经开始采用热疗辅助的放疗和化疗,在治疗过程中,适当地升高温度(通常在40~45 ℃之间)已被证明具有细胞毒性作用,使癌细胞更容易受到放疗和化疗的影响并且在给予足够热剂量的情况下能够诱导肿瘤细胞死亡[4]。
聚焦式微波热疗作为一种具有广阔前景的非侵入性热疗技术,近年来受到广泛关注[5-7]。该方案采用微波天线阵列进行微波波束成形,通过迭代的方法调整阵列中天线单元的激励相位和幅度,从而将微波能量选择性地聚焦在乳腺肿瘤上并加热肿瘤[8-9]。因此,当肿瘤被加热到42 ℃时,其周围健康组织的温度仍然很好地限制在安全范围内,很大程度降低了对正常组织不必要的灼伤。这种新的技术由于具有局部治疗肿瘤和抑制周围正常组织损伤的能力,因而具有高精度、高效率和低副作用的优点[9]。目前研究中常见的热治疗原型机为圆柱形[7, 10],聚焦天线阵列的排布不能覆盖足够多的肿瘤位置。同时采用的聚焦优化策略以粒子群算法和时间反演算法为主,聚焦效果不够理想而且实现难度大。实时聚焦监测成像系统的缺失,也使得聚焦热疗过程可靠度下降。
基于聚焦式微波热疗的优势和目前热疗原型机的不足,本文提出一种无创热治疗系统的临床原型,用于聚焦微波对乳腺癌细胞的靶向治疗。在该系统中,一组工作在2.45 GHz的天线阵列用于将微波能量经皮肤传送到浸没在耦合介质中的乳房内部。然后使用差分进化算法找到能够在给定肿瘤位置聚焦的天线相位,从而在肿瘤处产生最大热剂量。最后使用基于压缩感知的热声成像技术确定聚焦斑的位置是否达到要求,并及时调整天线阵列相位。本文利用该系统,在真实人体乳房模型内部实现了对直径1.5 cm的肿瘤聚焦,并观察到目标区域的明显聚焦现象。
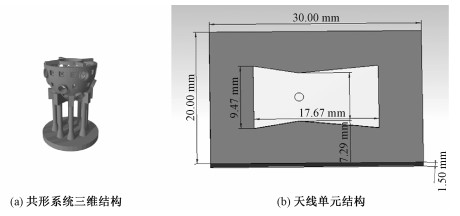
1 共形聚焦热疗系统设计一个完整的共形聚焦热疗系统主要由3个部分组成(见图 1)。第1部分是天线阵列及激励微波源。在该系统中使用24片工作频率为2.45 GHz的领结型贴片天线。所有的天线都分布在与乳房模型表面近似共形的半球表面上。对于一个体积较小的治疗原型而言,紧凑的小型化天线元件是首选,以便它们可以在考虑天线的耦合情况下尽可能多地配置在共形面上,用来提供足够大的热剂量用于治疗。考虑到天线阵列与乳房模型间填充的耦合液的影响,单个天线单元的参数都在耦合液背景下优化完成,优化目标是天线的回波损耗小于-10 dB;第2部分是超声传感器阵列及相应的信号放大器和数据采集系统。该系统采用圆形平面超声传感器。在本文提出的系统中,13个超声传感器与天线阵列部署在同一个半球面上。一般来说,传感器的探测区域越大,信号就越大。但在这种设计中需要考虑的一个折衷因素是贴片天线与超声传感器之间要保持适当距离,应选择适当的传感器尺寸以避免微波和声波信号之间发生严重的干扰。因此,在综合考虑多种因素后选用直径为2.5 cm的圆形超声传感器;第3部分是共形治疗系统的支撑结构。天线和传感器都固定在这个共形半球支架上。填充在共形腔内的耦合液体,将乳房内因聚焦在肿瘤上的电磁脉冲产生的声波信号耦合到超声传感器上。整个系统的示意图如图 1(a)所示,天线单元如图 1(b)所示。
|
Download:
|
| 图 1 共形热疗系统结构及天线单元 Fig. 1 Structures of the conformal system and antenna | |
在严重散射的环境中,特别是在具有电磁参数(介电常数及电导率)高度不均匀分布的致密人体乳房组织中,要在乳腺肿瘤处实现期望的微波场聚焦且不影响正常乳腺组织是非常具有挑战性的工作。因此,需要一些优化算法迭代寻找天线阵的最佳激励相位和幅度,以达到最佳的聚焦条件。在常见的圆柱状聚焦式微波热疗系统中, 粒子群优化(particle swarm optimization, PSO)算法被用于天线阵列的相位寻优聚焦[7]。然而相对于PSO算法,差分进化(differential evolution, DE)算法具有更好的全局寻优的特点[11]。
DE优化方法是基于群智能理论,通过粒子之间的合作与竞争产生新的粒子[12]。它具有优秀的鲁棒性和强大的全局搜索能力,已成功地应用于电力系统故障诊断和机器人等领域[13-14]。它需要设置的参数包括:变异因子(F)、交叉因子(Cr)、种群大小(M)、迭代次数(G)和问题的维度(N)。
变异操作是DE算法的核心,可以表述为
| $ \varphi (t + 1) = {\varphi _{{\rm{best}}}} + F[{\varphi _{r1}}(t) - {\varphi _{r2}}(t)]. $ | (1) |
式中:φbest代表当代种群中最好的个体,φr1和φr2是种群中两个随机选择的相位。
此外还需要定义适应度评价函数f作为优化结果的评价标准。优化的目的是在肿瘤处实现高度聚焦的微波场,并最大限度地减小健康组织中的场幅值,因此通过式(3)中给出的功率沉积密度函数Q,在式(2)中求解适应度评价函数
| $ f(Q) = {\mathop{\rm Max}\nolimits} \left( {\frac{{{Q_{{\rm{tumor }}}}}}{{{Q_{{\rm{health }}}}}}} \right), $ | (2) |
| $ Q = \sigma |{E_{{\rm{tot}}}}{|^2}. $ | (3) |
式中:σ表示电导率,Etot表示由所有天线元件贡献的总电场,Qtumor表示肿瘤中的平均功率密度,Qhealth表示健康组织区域中的最大功率密度。迭代优化的最终目的是最大化适应度评价函数f。
DE优化方法的伪代码如下所示
|
|
治疗位置已知的乳腺肿瘤的迭代聚焦过程从建立天线阵列的初始相位分布开始。然后利用具有初始相位分布的微波信号对乳房进行辐照。根据聚焦状态的反馈对天线的激励相位进行动态的调整。为了监测整个乳腺中相关的微波功率分布,需要利用一些监测技术,例如核磁共振成像[15]、微波成像[16]或热声成像[9]。在聚焦式微波热疗时,核磁共振成像和微波成像实际上获得的是乳房内部的温度信息,再由此导出功率分布。但是在聚焦尚未完成时,热量的提升是不明显的,因此难以通过温度信息重建功率分布。相比之下,热声成像技术能够直接呈现乳房内部的功率沉积分布。在聚焦脉冲微波作用下,由于乳腺肿瘤具有更大的电导率,因此肿瘤组织相对于正常乳腺组织能接收到更高的微波辐射。相应地,肿瘤产生的声波比它周围的健康组织产生的声波更强,在最终得到的热声图像中呈现为一个亮点。因此,用热声成像方法可以很容易地揭示乳房内部的微波功率分布,从而能够直接判断聚焦热疗是否达到了期望的聚焦效果。如果聚焦效果不够理想,则采用一定的优化算法产生下一组用于迭代优化的激励相位。一个迭代的过程,包括:1)确定激发相位;2)微波辐射乳房;3)监测功率沉积分布和评估聚焦条件。然后按照这样的顺序重复多次,最终达到在肿瘤处的聚焦微波场和在其他正常组织内的抑制场达到可接受的范围。
反投影是目前热声成像最广泛使用的成像算法[17]。但该算法对热声信号的空间测量量过大,硬件成本高,扫描时间长等缺点使其难以实现实时监测。聚焦式乳腺癌热疗中微波功率沉积的监测需要实时进行,以保证及时反馈聚焦状态,用以调整天线阵的激励相位和幅度分布。为了实现这一目标,本文利用压缩感知技术,实现高时效性的热声成像,用于监测热疗中的微波场聚焦状态[18]。
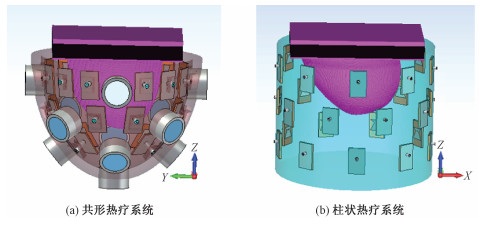
4 系统仿真实现基于DE聚焦算法的共形聚焦式热疗系统的CST软件仿真模型如图 2(a)所示, 基于PSO聚焦算法的传统柱状聚焦式热疗系统的仿真模型如图 2(b)所示。搭载了压缩感知实时成像的共形聚焦热疗系统为了能够获取足够多的内部信息用于图像重构还原,超声探头尽可能均匀地覆盖在乳房模型周围。两种模型都是先由CST完成整个乳房模型的电场仿真,再通过MATLAB处理每个天线对数字乳房模型的电场贡献结果。天线阵列单元的相位将通过调节DE算法进行优化,以确保将能量最大化集中在肿瘤处。在优化评估完成后,根据式(3)得到总场的分布和乳房模型内的功率沉积分布。
|
Download:
|
| 图 2 热疗系统结构示意图 Fig. 2 Prototypes of hyperthermia systems | |
对两种算法而言,第t次迭代的总电场是通过以下方法获得的
| $ E_{i, {\rm{ tot }}}^t = \sum\limits_{n = 1}^{24} {\exp } \left( {j\varphi _{i, n}^t} \right){E_n}. $ | (4) |
式中:En是由第n个天线单元引起的原始模拟电场,φi, nt表示第i个粒子(PSO)或第i个粒子(DE)在第t次迭代中的第n个天线单元的激发相位。
为了直观体现两种聚焦热疗模型在聚焦乳房热疗中的聚焦性能,先前的影像学研究被用来确定乳房组织的材料特性,这些数据被整合到一个多物理乳房模型中。本文选用内部腺体分布致密的乳房模型内嵌1.5 cm直径的肿瘤,检验复杂情况下的两种算法聚焦能力。虽然天线阵列的激励相位和幅度都会影响非均匀物体中微波场的波束形成及聚焦结果,但是相位的影响通常占据主导地位[7]。因此,本文只考虑激励相位的优化,即所有天线单元的幅度保持相同,这样可以简化问题,也不影响两种算法性能的比较。表 1总结了两种算法的参数选择,其中对于PSO算法ω(t)是随时间变化的惯性权重,惯性权重在优化开始时是最大的,以保证全局优化的良好性能,然后逐渐减小以保证精度。c1是局部学习因子,c2是全局学习因子[19]。对于聚焦应用,需要最大化适应度函数值f(Q)。同时为了观察算法的后期优化特性,因此只设置迭代停止次数。考虑迭代的时间和资源成本综合选取迭代终止次数为100次,种群大小为15个。
|
|
表 1 算法仿真参数选择 Table 1 Parameter selection |
乳房模型内部的电导率分布剖面图如图 3(a)所示,基于两种不同系统的功率沉积分布优化如图 3(b)、3(c)所示。利用两种治疗原型系统,乳房模型内部明显的功率沉积都能在肿瘤的正确位置处显现。但是可以清楚地观察到,基于DE聚焦算法的共形治疗系统优于PSO方法,因为它在肿瘤处实现了更好的聚焦场,并且在乳房模型的健康组织中实现了更少的功率沉积,即减少了正常组织被灼伤的可能。在共形系统的实时成像部分,功率沉积优化后的功率分布将作为参量被导入用于声压计算,13个探头的相对于乳房模型的实际位置被记录用于构建声压信息和压缩感知算法所需要的稀疏字典。上述步骤完成后采用文献[20]所示算法,在成像域内恢复出乳房模型内的功率沉积分布。恢复的乳房内部功率沉积如图 4(c)所示,可以看到仿真得到的功率沉积分布与压缩感知热声成像恢复出的图像具有良好的对应性,因此为聚焦状态的判别提供了可靠的依据。

|
Download:
|
| 图 3 乳房模型内部电导率及算法优化后功率分布 Fig. 3 Profiles of conductivity(a) and power depositions after optimization with different algorithms(b, c) within breast | |

|
Download:
|
| 图 4 热声成像功率恢复验证 Fig. 4 Power deposition with DE optimization and image restoration by compressed sensing | |
本文提出一种基于DE算法的共形聚焦热疗系统,与传统的圆柱型治疗系统相比,共形治疗系统共形面上的天线能够覆盖乳房内更多的空间位置,使得聚焦斑的位置更加可控。同时以PSO算法优化的结果作为参照,与传统的PSO算法的柱状聚焦热疗系统相比,采用DE聚焦方案的共形聚焦系统具有更好的聚焦特性,提供了更好的治疗效果。共形聚焦式热疗系统集成实时成像部分,为聚焦热疗提供可视化的聚焦判断,提高了聚焦式热疗的安全性。
| [1] |
Bray F, Ferlay J, Soerjomataram I, et al. Global cancer statistics 2018:GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries[J]. CA:A Cancer Journal for Clinicians, 2018, 68(6): 394-424. Doi:10.3322/caac.21492 |
| [2] |
Stauffer P R, Maccarini P, Arunachalam K, et al. Conformal microwave array (CMA) applicators for hyperthermia of diffuse chest wall recurrence[J]. International Journal of Hyperthermia, 2010, 26(7): 686-698. Doi:10.3109/02656736.2010.501511 |
| [3] |
Cheng K S, Dewhirst M W, Stauffer P R, et al. Effective learning strategies for real-time image-guided adaptive control of multiple-source hyperthermia applicators[J]. Medical physics, 2010, 37(3): 1285-1297. |
| [4] |
Jones E, Thrall D, Dewhirst M W, et al. Prospective thermal dosimetry:the key to hyperthermia's future[J]. International Journal of Hyperthermia, 2006, 22(3): 247-253. Doi:10.1080/02656730600765072 |
| [5] |
Falk M H, Issels R D. Hyperthermia in oncology[J]. International Journal of Hyperthermia, 2001, 17(1): 1-18. Doi:10.1080/02656730118511 |
| [6] |
Saniei N. Hyperthermia and cancer treatment[J]. Heat Transfer Engineering, 2009, 30(12): 915-917. Doi:10.1080/01457630902854371 |
| [7] |
Nguyen P T, Abbosh A, Crozier S. Three-dimensional microwave hyperthermia for breast cancer treatment in a realistic environment using particle swarm optimization[J]. IEEE Transactions on Biomedical Engineering, 2017, 64(6): 1335-1344. Doi:10.1109/TBME.2016.2602233 |
| [8] |
Patch S K, Hull D, Thomas M, et al. Thermoacoustic contrast of prostate cancer due to heating by very high frequency irradiation[J]. Physics in Medicine & Biology, 2015, 60(2): 689. |
| [9] |
Lou C, Yang S, Ji Z, et al. Erratum:ultrashort microwave-induced thermoacoustic imaging:a breakthrough in excitation efficiency and spatial resolution[Phys. Rev. Lett. 109, 218101(2012)][J]. Physical Review Letters, 2014, 112(11): 119904. Doi:10.1103/PhysRevLett.112.119904 |
| [10] |
Stang J, Haynes M, Carson P, et al. A preclinical system prototype for focused microwave thermal therapy of the breast[J]. IEEE Transactions on Biomedical Engineering, 2012, 59(9): 2431-2438. Doi:10.1109/TBME.2012.2199492 |
| [11] |
Cappiello G, Mc Ginley B, Elahi M A, et al. Differential evolution optimization of the SAR distribution for head and neck hyperthermia[J]. IEEE Transactions on Biomedical Engineering, 2017, 64(8): 1875-1885. Doi:10.1109/TBME.2016.2627941 |
| [12] |
Storn R, Price K. Differential evolution:a simple and efficient heuristic for global optimization over continuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341-359. Doi:10.1023/A:1008202821328 |
| [13] |
Cai H R, Chung C Y, Wong K P. Application of differential evolution algorithm for transient stability constrained optimal power flow[J]. IEEE Transactions on Power Systems, 2008, 23(2): 719-728. |
| [14] |
Das S, Suganthan P N. Differential evolution:a survey of the state-of-the-art[J]. IEEE Transactions on Evolutionary Computation, 2011, 15(1): 4-31. |
| [15] |
Hynynen K, McDannold N. MRI guided and monitored focused ultrasound thermal ablation methods:a review of progress[J]. International Journal of Hyperthermia, 2004, 20(7): 725-737. Doi:10.1080/02656730410001716597 |
| [16] |
Haynes M, Stang J, Moghaddam M. Real-time microwave imaging of differential temperature for thermal therapy monitoring[J]. IEEE Transactions on Biomedical Engineering, 2014, 61(6): 1787-1797. Doi:10.1109/TBME.2014.2307072 |
| [17] |
Xu M, Xu Y, Wang L V. Time-domain reconstruction algorithms and numerical simulations for thermoacoustic tomography in various geometries[J]. IEEE Transactions on biomedical engineering, 2003, 50(9): 1086-1099. Doi:10.1109/TBME.2003.816081 |
| [18] |
Xu L, Wang B, Lin Z, et al. A novel monitoring technique for breast cancer hyperthermia using thermoacoustic imaging[C]//2018 International Workshop on Antenna Technology (iWAT). IEEE, 2018: 1-4.
|
| [19] |
贾志成, 王娜娜, 陈雷, 等. 基于非线性函数和简化粒子群优化的盲源分离算法[J]. 中国科学院大学学报, 2014, 31(4): 530-536. |
| [20] |
田野, 张冰尘, 洪文. 基于分布式压缩感知的重轨干涉SAR形变检测方法与实验[J]. 中国科学院大学学报, 2016, 33(1): 107-114. |
 2020, Vol. 37
2020, Vol. 37 


