随着物联网的快速发展，各类移动智能设备需要处理的任务量不断提高。比如，应用增强现实技术的在线交互游戏设备需要大量计算和通信资源。因此，传统的个人电脑、智能手机等移动设备和物联网设备在电池和计算能力方面面临巨大的挑战。一个经典的解决方案是将这些任务卸载到能源、存储和计算资源丰富的云端服务器^[1]，但是远距离云端传输将会带来额外的通信时间。为了满足低时延的服务要求，研究人员提出利用雾计算节点(如具有闲置可用资源的移动、物联网设备)数量庞大、无处不在的天然优势，将计算、存储、控制和通信服务分布在云到雾的连续体中。因此，为了更好地利用周围的雾节点，急需一个高效的算法，来决定在雾计算网络中哪些计算任务需要卸载以及应卸载到哪个节点。

一般来说，把高复杂度的计算任务卸载到其他的节点上能够有效地节约本地节点的计算资源与能量资源。在一些文献中，任务卸载被建模为确定性优化问题，例如，Dinh等^[2]研究的能量和延迟的联合最小化，以及You等^[3]研究的延迟约束下的能耗最小化。然而，一个实用的任务卸载策略需要依赖于用户和服务器的实时状态，例如，计算队列的长度等信息。从这个方面来说，因计算队列长度的不确定性，任务卸载是典型的随机规划问题，传统的基于确定性参数的优化方法并不适用。为了解决这个问题，在文献[4-7]中，研究人员调用李雅普诺夫(Lyapunov)优化方法，将具有挑战性的随机规划问题转换为顺序决策问题，其中包括每个时隙中的一系列确定性问题。此外，Chen^[8]提出一种基于博弈论的分布式解决方案，每个用户可以自主地进行卸载决策。

上述文献中提出的任务卸载方案都假定可以获得关于系统参数的全部信息。但是，在实际系统中，存在参数在用户处未知或部分已知的情况。例如，一些特定的值可能只能作为后验信息，当特定节点被访问时才能获得。Chen和Giannakis^[9]将每个任务的通信延迟和计算延迟视为后验信息。Tekin和Van Der Schaar^[10]假设每个用户的移动性是不可预测的。在实际系统中，可用资源通常是有限的，从而导致每次决策可访问的节点数量非常有限。此时，若以最小化长期开销为目标，所做出的决策就必须平衡“探索”与“开发”之间的权重。一方面，为了减小眼前的开销，决策应偏向尽可能“开发”经验最佳节点；另一方面，从长远角度考虑，用户需要“探索”其他节点以找到潜在的性能更优的节点。为了平衡这种关系，一种流行的方法是将“探索”与“开发”困境建模为多臂老虎机(MAB，multi-armed bandit)^[11-13]问题。这一理论模型在统计学中受到广泛关注^[13]。

在雾计算网络任务卸载的研究中，很少有先前的工作研究这种探索与开发权衡的关系，本文将详细探讨这个问题。首先，假设每个任务的准确的处理时延在任务处理之前是未知的。基于此，尝试基于有限的反馈提出一种高效的任务卸载算法，从而最小化用户长期时延。因此，引入一个非稳态多臂老虎机模型以捕捉随机且未知的时延变动。相比于以往如文献[2-7]中的确定性模型，该随机模型更加符合实际模型。之后，基于置信上界(UCB, upper-confidence bound)策略提出一种高效的任务卸载算法。由于该算法不是直接的UCB策略的应用，因此传统的理论分析无法直接适用。针对这一改进版的UCB算法，将从理论层面给出算法的性能保证。

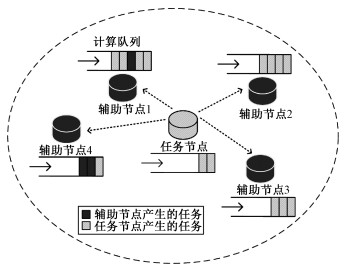
1 系统模型 1.1 网络模型

考虑一个雾赋能的网络(参见图 1)，其中雾节点按照其功能可分为任务节点和辅助节点两类。每个雾节点都有可能产生计算任务，也可以与附近的节点通信。假定每个节点未完成的任务被缓存在各自节点的先入先出(FIFO, first-input-first-output)队列中。由于单一节点内的计算和存储资源有限，在本地处理的任务通常会经历较高延迟，这会降低服务质量(QoS, quality of service)和体验质量(QoE, quality of experience)。为了实现低延迟处理，一个任务节点可以将其一些计算任务卸载到附近的辅助节点。这些辅助节点通常拥有更多的计算和存储资源，并且可以按需部署以帮助其他任务节点。在诸如在线游戏等典型应用中，任务通常是周期性地生成的，并且不能任意拆分。因此，假设每个节点在每个时隙t的开始生成一个任务t，该任务可以作为一个整体由本地节点计算或者分配给一个相邻的辅助节点。

本文的目标是最小化一个特定任务节点的长期时延。特别地，考虑如下所示集合中的K个雾节点：

$ \mathcal{I}:=\{\underbrace{1,2,\cdots ,K-1}_{\text{ Helper}\text{nodes }},\underset{\begin{smallmatrix} \left. \right\} \\ \text{ Task}\text{node } \end{smallmatrix}}{\mathop{K}}\,\}. $

(1)

在本文中，假设任务节点不能将任务卸载到正在与其他节点通信的辅助节点。还假设每个任务都是独立生成的，且任务节点之间不合作。

用T(i)表示传输每一比特信息到节点i所需要的时间，它是一个依赖于距离的值，并且可以在传输前进行测量。在这里，假设不同任务节点占用预先分配的正交时间或频谱资源与辅助节点通信，如TDMA或FDMA。任务t的数据长度用L_t表示，假设任务大小传输延迟L_tT(i)不超过一个时隙。在本地处理的任务传输延迟为零，即L_tT(K)=0。

用Q_t(i)表示节点i在时隙t开始时的任务队列长度。同时，W_t(i)表示节点i处理每一比特队列中的任务所需的时间，P_t(i)表示节点i处理任务t中每一比特所需的时间。在本文中，变量W_t(i)和P_t(i)被定义为随机变量，它们的数学期望分别为

$ \mu _t^W(i): = \mathbb{E}[{W_t}(i)],\mu _t^P(i): = \mathbb{E}[{P_t}(i)]. $

(2)

假设每个任务的总时延主要由上述时延构成，即传输时延L_tT(i)、队列中的等待时延Q_t(i)W_t(i)以及处理时延L_tP_t(i)。传输计算结果等反馈信息所需要的时延在本文中不考虑。根据上述定义，将任务t分配给节点i处理所需的时延可以定义为

$ {U_t}(i): = {L_t}T(i) + {Q_t}(i){W_t}(i) + {L_t}{P_t}(i). $

(3)

在进一步分析问题之前，给出下列假设：

·假设1：时延U_t(i)在任务t处理完之前是未知的；

·假设2：队列长度Q_t(i)在每个时隙t开始时由节点i广播至各个雾计算节点；

·假设3：等待时延和处理时延，即L_tT(i)和Q_t(i)W_t(i)，遵循未知随机分布。相应的数学期望，即μ_t^W(i)和μ_t^P(i)，会在未知时间点突变。这些时间点称作断点。

与文献[2-7]中基于已知系统参数的模型的任务卸载问题不同，我们在假设1和假设3中对CPU频率等系统参数与处理延迟之间的关系没有任何限制，文献[9]中也体现出这一思想。这是更加实际的设置，原因如下。首先，任务的复杂度等变量应该被建模为一系列独立的随机变量。这是因为计算本身的不确定性，而且它们的分布可能会由于任务类型的变化而发生突变例如，移动用户在使用不同应用程序时，任务类型、任务复杂度等参数会发生改变^①。另外，节点的计算能力，例如每个节点所分配用于计算的CPU频率、CPU内核数目、内存大小等都有差异，而且也可能会发生突变。上面提到的所有这些不确定性使得系统难以预测单一节点处理不同任务的时延。而且，单个节点获取系统的全局节点的信息会花费大量通信开销。在传统模型中，如Mao等^[5]假设时延简单地由任务数据长度和配置的CPU频率决定，然而在实际系统中，单个任务节点很难像传统模型那样准确地估计计算时延和等待时延。

①  例如,移动用户在使用不同应用程序时,任务类型、任务复杂度等参数会发生改变。

本文中，处理时延和等待时延仅在相应的任务处理结束之后反馈给系统。也就是说，等待时延的观测值τ_t^W和处理延迟的观测值τ_t^P被视为后验信息。这些时延信息可以通过相应节点完成任务后的时间戳反馈获得。因此，随机变量W_t(i)和P_t(i)在每一时刻的样本值可以由以下公式计算得到：

$ {w_t}(i) = \frac{{\tau _t^W}}{{{Q_t}(i)}}1\{ {I_t} = i\} ,{p_t}(i) = \frac{{\tau _t^P}}{{{L_t}}}1\{ {I_t} = i\} , $

式中：I_t表示处理任务t的节点的编号；1{·}为指示函数，当花括号内条件满足时，该函数取值为1，否则为0。

1.2 问题建模

般的长期平均时延最小化问题可以被建模成如下形式：

$ \begin{array}{*{20}{l}} {\mathop {{\rm{minimize}}}\limits_{\{ {I_t},\forall t\} } {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathop {{\rm{lim}}}\limits_{T \to \infty } \frac{1}{T}\sum\limits_{t = 1}^T {\sum\limits_{i = 1}^K {{U_t}} } (i)1\{ {I_t} = i\} }\\ {{\rm{subject}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{to}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {I_t} \in \mathcal{I},t = 1,2, \cdots ,T.} \end{array} $

(4)

解决上述问题有两个困难。首先，它是一个随机规划问题。在第t个任务完成之前，无法得到时延U_t(i)的确切信息。另外，即使U_t(i)为已知的先验信息，这个问题仍然是组合优化问题，复杂度为 $\mathcal{O}$(K^T)量级。这是因为先前的卸载决策确定了每个雾节点中的队列长度，并进一步影响未来任务的决策。有关示例，请参阅文献[10]。为使任务卸载策略具备在线更新、动态调整的能力，一种流行的方法是在每个时间段将这个具有挑战性的随机和组合优化问题转换为一个低复杂度的顺序决策问题^[2-7]。基于在之前的(t－1)个时隙中做出的任务卸载决策，最优策略变为将任务t卸载到t时刻能够获得最低时延的节点。同时，在随机问题的框架下^[12]，关注随机变量的期望是更自然的做法，即代码 $\mathbb{E}$[U_t(i)]。因此，表达式(4)中的问题在第t个时隙中变成以下问题：

$ \mathop {{\rm{ minimize }}}\limits_{{I_t} \in \mathcal{I}} \sum\limits_{i \in \mathcal{I}} \mathbb{E} [{U_t}(i)]1\{ {I_t} = i\} . $

(5)

然而，上述公式仍然是随机规划问题。将经验平均值作为期望 $\mathbb{E}$[U_t(i)]的估计值虽然可行，但此信息可能由于观察数量有限而不准确。值得注意的是，有关节点i的信息来自节点i在完成相应任务时的反馈，因此为了获得某个特定节点更准确的信息，任务节点必须将更多任务卸载到该节点，即使它可能不是经验上最好的卸载节点。因此，在这个问题中存在探索和开发的权衡。下文致力于找到一种有效的方案来解决表达式(5)中的问题。

2 高效的任务卸载策略 2.1 基于SW-UCB的任务卸载

当某个任务产生时，需要确定一个雾节点(辅助节点或任务节点)来处理它。与此同时，必须在上述探索和开发之间取得平衡。这种权衡促使我们诉诸老虎机模型。具体来说，任务卸载被建模为非稳态多臂老虎机(MAB)问题^[14]，其中 $\mathcal{I}$中的每个节点被视为老虎机的一个操纵杆(arm)。

按照前面的假设，任务节点在每个时隙开始时产生一个任务。令τ_s≤s+τ_max为收到第s个任务反馈的时间，其中τ_max是最大容许时延。如果任务时延超过最大容许时延，即τ_s>s+τ_max，该任务视为失败并被丢弃。根据文献[14]，随机变量W_t(i)和P_t(i)的估计值可以由历史观测值的滑动窗口平均值得到，即

$ \begin{array}{*{20}{l}} {{{\bar W}_t}(\tau ,i): = \frac{1}{{{N_t}(\tau ,i)}}\sum\limits_{s = t - \tau }^{t - 1} {{w_s}} (i)1\{ {I_s} = i,{\tau _s} \le t\} ,}\\ {{{\bar P}_t}(\tau ,i): = \frac{1}{{{N_t}(\tau ,i)}}\sum\limits_{s = t - \tau }^{t - 1} {{p_s}} (i)1\{ {I_s} = i,{\tau _s} \le t\} ,} \end{array} $

(6)

式中τ>0表示滑动窗口的长度，以及

$ {N_t}(\tau ,i): = \sum\limits_{s = t - \tau }^{t - 1} 1 \{ {I_s} = i,{\tau _s} \le t\} . $

(7)

那么，时延U_t(i)就可以被估计为

$ {\bar \mu _t}(\tau ,i): = {L_t}T(i) + {Q_t}(i){\bar W_t}(\tau ,i) + {L_t}{\bar P_t}(\tau ,i). $

(8)

注意到式(8)中的延迟是根据W_s(i)和P_s(i)的历史信息估算的，而不是之前的延迟值，即U_s(i), s < t。这是因为时延U_s(i)严重依赖于队列长度Q_t(i)和任务长度L_t，这对于不同的任务、不同的节点可能会有很大差异。因此，直接用之前的时延观测值估计U_t(i)是不可靠的。另一方面，处理每一个比特的任务所需的时间通常由节点能力和任务类型确定，这些因素相对稳定并因此适合用样本均值估计。

将节点i用于处理任务t的总时间与最大容忍时延进行比较，定义该时间差为完成任务的奖励，即X_t(i):=τ_max－U_t(i)。显然，负的奖励表示任务失败。根据式(8)中所估计的时延，奖励的估计值由下式给出

$ {\bar X_t}(\tau ,i): = {\tau _{{\rm{max}}}} - {\bar \mu _t}(\tau ,i). $

(9)

我们用UCB算法来权衡探索和开发之间的关系。从本质上来说，这种折中关系由探索奖励c_t(τ, i)来衡量，即探索节点i会有额外的奖励。在本文中，令

$ {c_t}(\tau ,i): = {\tau _{{\rm{max}}}}\sqrt {\frac{{\xi {\rm{ln}}(t \wedge \tau )}}{{{N_t}(\tau ,i)}}} , $

(10)

式中：ξ表示探索常数，t∧τ表示取t和τ之间的最小值。按照这种方式选取探索奖励c_t(τ, i)的好处将在后文分析。根据该置信上界，即${{\bar X}_i}(\tau , t) + {c_i}(\tau , t)$，用来处理任务t的节点可按照如下方式选择：

$ {I_t} = {\rm{argmax}}{ _{i \in \mathcal{I} }}{\bar X_t}(\tau ,i) + {c_t}(\tau ,i). $

(11)

本文算法的具体流程见算法1。

算法1   TOS(task offloading with sliding-window-UCB)任务卸载算法

步骤1)  设置合适的窗长参数τ。设置索引t=1，${{\bar W}_t}(\tau , i) = {{\bar P}_t}(\tau , i) = 0$, ∀i∈ $\mathcal{I}$。

步骤2)  令I_t=t，卸载任务t至节点I_t；

步骤3)   t=t+1；

步骤4)   若t>K，转至步骤5)；否则跳转至步骤2)；

步骤5)  根据式(6)、式(7)更新参数${{\bar W}_t}(\tau , i), {{\bar P}_t}(\tau , i)$和N_t(τ, i)。

步骤6)  根据式(9)、式(10)更新参数${{\bar X}_i}(\tau , t)$，c_t(τ, i)。

步骤7)  根据式(11)做出决策I_t，卸载任务t至节点I_t；

步骤8)   t=t+1；

步骤9)   若t>T，算法结束；否则跳转至步骤5)。

由算法1可知，本文算法的复杂度主要集中于步骤5)。若直接按照式(6)、式(7)执行步骤5)，则该步骤复杂度为 $\mathcal{O}$(Kτ)。因此，在执行每一次任务卸载时，决策复杂度为 $\mathcal{O}$(Kτ)。若步骤5)采取增量更新的方式，只关注最新移入或移出窗口的部分，每次决策的复杂度可进一步降低为 $\mathcal{O}$(K)。根据假设2，为保障算法运行，每个节点广播其队列长度。因此，对于算法本身来说，功耗主要集中于广播队列长度以及执行决策的功耗。此外，任务卸载本身还包含实际卸载任务的功耗(任务节点承担)以及实际执行任务的功耗(按需部分由辅助节点承担)。

虽然上面提出的任务卸载模型本质上是一个非稳态的MAB模型，但与文献[14]中提出的传统模型相比，存在两个主要差异。首先，在传统模型中，决策的反馈是即时获得的。而在我们的模型中，如式(6)所示，在任务完成之前，即τ_s≤t时，反馈是无法得到的。而相应的延迟是无法忽略的，因为它恰好是我们需要的信息。值得注意的是，延迟的反馈会影响算法性能，这一现象被Joulani等指出并在文献[15]中分析。其次，常规的非稳态MAB模型^[14]假设最好的节点只在断点处改变。但是，我们的模型允许最佳节点在不同时刻、处理不同任务时发生变化。因此，目前已有的SW-UCB算法的性能保证不能直接应用于我们提出的TOS。

2.2 理论分析

根据式(2)和式(3)，期望时延 $\mathbb{E}$[U_t(i)]可以表示为

$ \begin{array}{*{20}{l}} {{\mu _t}(i): = \mathbb{E}[{U_t}(i)] = {L_t}T(i) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {Q_t}(i)\mu _t^W(i) + {L_t}\mu _t^P(i).} \end{array} $

给定前(t－1)个任务的卸载策略，根据式(5)，处理任务t的最优节点为i_t^*:=argmin_{i∈ $\mathcal{I}$}μ_t(i)。此外，用

$ {\tilde N_T}(i): = \sum\limits_{t = 1}^T 1 \{ {I_t} = i \ne i_t^*\} $

表示前T个时隙中节点i为非最优节点时所获得的任务数量。根据假设3，系统参数的期望值在每个断点会发生突变。用Ƴ_T表示时刻T之前的断点数目。以下推论给出$\mathbb{E}({{\tilde N}_T}(i))$的上界。

推论1   假设ξ>1/2。对于每个节点i∈ $\mathcal{I}$，期望$\mathbb{E}({{\tilde N}_T}(i))$的上界为

$ \begin{array}{*{20}{l}} {\mathbb{E}[{{\tilde N}_T}(i)] \le \frac{{T{\rm{ln}}\tau }}{\tau }B(\tau ) + {Ƴ _T}(\tau + {\tau _{{\rm{max}}}}) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{2{{({\rm{ln}}\tau )}^2} + 2{\rm{ln}}\tau }}{{{\rm{ln}}(1 + \eta )}},} \end{array} $

(12)

其中

$ {B(\tau ): = \left( {\frac{{4U_{{\rm{max}}}^{\rm{2}}\xi }}{{{{(\Delta {\mu _T}(i))}^2}}} + {\tau _{{\rm{max}}}}} \right)\frac{{T/\tau }}{{T/\tau }} + 2\frac{{\left\lceil {\frac{{{\rm{ln}}\tau }}{{{\rm{ln}}(1 + \eta )}}} \right\rceil }}{{{\rm{ln}}\tau }},}\\ {\Delta {\mu _T}(i): = {\rm{mi}}{{\rm{n}}_{t \in \{ 1, \cdots ,T\} ,i_t^* \ne i}}{\mu _t}(i) - {\mu _t}(i_t^*).} $

证明见附录。显然，该上界取决于总任务数T、断点数Ƴ_T以及窗长τ的选择。从式(12)中，可以看出第1项(TB(τ)lnτ)/τ随着τ增加而减少。另一方面，后面两项，即Ƴ_T(τ+τ_max)和(2(lnτ)²+2lnτ)/ln(1+η)，随着τ增加而增加。这种折中关系与我们的直觉一致，即更高的窗口长度τ有助于在稳定情况下更好地估计，但同时导致对环境突然变化的缓慢反应。因此，在式(12)中的不同项之间存在权衡。为了在稳定和突然变化的环境之间取得平衡，类似于文献[14]，将τ定义为

$ \tau = 2{\tau _{{\rm{max}}}}\sqrt {(T{\rm{ln}}T)/{Ƴ_T}} . $

(13)

相应地，有以下推论。

推论2   当Ƴ_T= $\mathcal{O}$(T ^β), β∈[0, 1)，以及T→∞时，期望$\mathbb{E}[{{\tilde N}_T}(i)]$的数量级为

$ \mathbb{E}[{\tilde N_T}(i)] = \mathcal{O} (\sqrt {T{Ƴ_T}{\rm{ln}}T} ). $

证明  令$\tau = 2{\tau _{\max }}\sqrt {(T\ln T)/{Ƴ_T}} $，取T→∞，易得。

为了证明所提出的算法的最优性，定义卸载前T个任务的伪后悔度为

$ {\zeta _T}: = \frac{1}{T}\mathbb{E}[\sum\limits_{t = 1}^T {({U_t}(} {I_t}) - \mathbb{E}[{U_t}(i_t^*)])]. $

(14)

关于ζ_T，有如下推论。

推论3   当Ƴ_T= $\mathcal{O}$(T ^β), β∈[0, 1)时，算法1中的算法是渐进最优的，即

$ \mathop {{\rm{lim}}}\limits_{T \to \infty } {\zeta _T}\mathop \to \limits^{{\rm{a}}{\rm{.s}}{\rm{.}}} 0. $

(15)

证明  注意到U_t(I_t)－$\mathbb{E}$[U_t(i_t^*)]≤τ_max1{I_t≠i_t^*}。伪后悔度可放缩为

$ \begin{array}{*{20}{l}} {{\zeta _T} \le \frac{1}{T}\mathbb{E}[\sum\limits_{t = 1}^T {{\tau _{{\rm{max}}}}} 1\{ {I_t} \ne i_t^*\} ]}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \le \frac{{{\tau _{{\rm{max}}}}}}{T}\sum\limits_{i \in \mathcal{I} } \mathbb{E} [{{\tilde N}_T}(i)].} \end{array} $

根据推论1和推论2，有

$ {\zeta _T} = \mathcal{O}(\sqrt {({Ƴ_T}{\rm{ln}}T)/T} ) = \mathcal{O}({T^{\frac{{\beta - 1}}{2}}}\sqrt {{\rm{ln}}T} ). $

那么对于任意ε>0，存在一个有限整数N_ε，使得

$ \mathbb{P}(|{\zeta _T}| \ge \varepsilon ) = 0,\forall T \ge {N_\varepsilon }. $

因此，

$ \sum\limits_{T = 1}^\infty \mathbb{P} (|{\zeta _T}| \ge \varepsilon ) \le {N_\varepsilon } < \infty . $

上述表达式表明$\mathop {\lim }\limits_{T \to \infty } {\zeta _T}\mathop \to \limits^{{\rm{a}}.{\rm{s}}.} 0$。证毕。

推论3说明，在条件Ƴ_T=$\mathcal{O}$(T ^β), β∈[0, 1)下，当T→∞时，该算法的后悔度以概率为1趋近于零。由$\mathop {\lim }\limits_{T \to \infty } |{\zeta _{T + 1}}|/|{\zeta _T}| = (\beta + 1)/2$知，该算法线性收敛。

3 仿真实验

在这一章节中，通过仿真10⁴次任务卸载来验证本文提出的算法。每次任务卸载时，任务节点产生一个任务。以下是各个场景中共同的仿真参数设定。

·该雾赋能的网络包含1个任务节点和9个辅助节点；

·每个时隙长度为20 ms。任务数据长度服从Unif(1, 15) KB；

·最大允许时延为τ_max=20时隙，参数ξ=0.6；

·每一比特任务的处理时延按照公式P_t(i)=σ_t^cplx/σ_i^CPU仿真，其中σ_t^cplx表示任务t的复杂度，σ_i^CPU反映节点i的计算能力。二者服从分布Unif(1, 10)；

·节点i的计算能力在断点处的变化遵从σ_i^CPU=σ_i^CPU/16或者σ_i^CPU=σ_i^CPU×16。

将算法TOS的性能与两个基本的策略(贪婪算法和轮询算法)、以及我们之前提出的基于折扣因子的在线任务卸载算法^[16]，即TOD(task offloading with discounted-UCB)算法，进行比较^①。在贪婪算法中，假设任务节点已知任务卸载相关随机变量的每一个样本值，并在每个时隙将任务卸载给时延最小的节点。值得注意的是，虽然贪婪算法代表每一时刻所能做出的最优决策，但该贪婪算法不是因果的，现实中不能实现。此外，由于当前时刻决策与下一时刻状态相互耦合，每一时刻的最优决策联合起来并不一定代表问题(4)的最优解。在轮询算法中，每个任务以循环的方式依次分配给各个雾节点。在TOD算法中，基于D-UCB框架，利用折扣因子γ应对非稳态环境。据我们所知，TOD算法为符合本文场景的最新算法。

① 注意到本文的核心问题在于，当任务卸载的代价需通过在线学习获得时，如何权衡“探索”和“开发”之间的折中关系。因此，其他预知代价的算法，如文献[5-8]中提到的李雅普诺夫(Lyapunov)优化方法，在本文中难以直接适用。

在图 2中，通过仿真不同的断点数目，TOS算法的有效性和稳定性得到证明。算法性能通过仿真中各个任务的时延的累积分布函数(CDF, cumulative distribution function)来体现。图中，TOD算法的折扣因子γ和TOS算法的滑动窗口长度τ各自按照其理论公式计算得到。图 2中的两个场景都证明TOS算法的性能远远优于轮询算法，接近于贪婪算法，并且略微优于TOD算法。在图 2(a)中，当断点数目Ƴ_T设置成150时，平均每67个任务就会有一次系统参数的突变。这暗示着TOS算法能够快速学习并适应频繁的系统变化，并且适应能力在一定程度上优于TOD算法。同样值得注意的是，从图 2(b)可以看出，当系统变化次数非常有限(Ƴ_T=10)时，TOS甚至表现出比贪婪算法更小的平均时延。这一现象揭示每个时隙的最优决策组合起来并不一定是全局最优这一事实。同时，这也佐证了我们之前的分析，即节点的每一时刻的决策都会影响系统后续的状态，进而影响后续的决策。

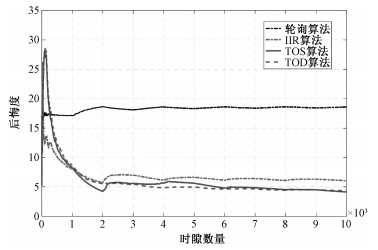
图 3绘制了不同方案的后悔度曲线。仿真中，后悔度的计算根据${{\hat \zeta }_T}: = \sum\nolimits_{t = 1}^T {\left( {{U_t}\left( {{I_t}} \right) - {U_t}\left( {{i_t}} \right)} \right)} /T$，其中每一时刻的最优决策基于该时刻的真实样本值，即i_t=argmax_{i∈$\mathcal{I}$}U_t(i)。在无限冲激响应(IIR)方案中，探索和开发分为两个阶段。探索阶段采用轮询的方式。在开发阶段，按照文献[16]中加权平均的方法将历史信息按照折扣因子γ加权求和。这一方法刚好对应了传统信号处理方法中的IIR滤波器。两个阶段最优的分配比例采用二分法搜索的方式以得到最小化后悔度的数值解。从图 3中，可以看出，本文提出的TOS算法和之前提出的TOD算法相较于轮询算法和IIR算法都能够达到更低的后悔度。这表明我们提出的方案在处理探索和开发的折中关系时表现优秀。

4 结束语

本文研究雾赋能的网络中一种高效的在线任务卸载策略以及相应的性能保证。考虑到节点处理速度的期望可能在未知时刻发生突变，并且相关系统参数信息仅在完成相应任务之后才获得这一场景，将任务卸载问题建模成带有延迟老虎机反馈的随机优化问题。为解决这个问题，基于UCB算法提供一个高效的在线任务卸载方案，即TOS。给定特定数量的断点Ƴ_T，证明卸载到非最佳节点的任务数量的上界是${\cal O}\left( {\sqrt {T{Ƴ_T}\ln T} } \right)$。此外，还证明，当任务数量趋近于无穷大时，伪后悔度以概率为1趋近于零。数值仿真证明，所提出的TOS算法能够在非稳态环境中学习并选择正确的节点以卸载任务，且表现优于TOD算法。

附录

证明   首先，根据定义做如下事件分解：

$ {\tilde N_T}(i) \le \sum\limits_{t = K + 1}^T 1 \{ {I_t} = i \ne i_t^*,{N_t}(\tau ,i) < A(\tau ,i)\} + \sum\limits_{t = K + 1}^T 1 \{ {I_t} = i \ne i_t^*,{N_t}(\tau ,i) \ge A(\tau ,i)\} + 1, $

其中A(τ, i)是参数τ的函数，具体形式将在后文给出。接下来，依次给出上述两个求和项的上界。第1项上界的推导需要借助文献[14]中的引理1，即对于任意的i∈$\mathcal{I}$, τ>0, m>0，下列不等式成立：

$ \sum\limits_{t = K + 1}^T 1 \{ {I_t} = i,\sum\limits_{s = t - \tau }^{t - 1} 1 \{ {I_s} = i\} < m\} \le \left\lceil {T/\tau } \right\rceil m. $

此外，将从时隙(t－τ)到时隙(t－1)期间缺失的反馈数量表示为

$ {G_t}(\tau ,i): = \sum\limits_{s = t - \tau }^{t - 1} 1 \{ {I_s} = i\} - {N_t}(\tau ,i). $

显然，缺失的反馈数目小于τ_max，即G_t(τ, i)≤τ_max, ∀t, i。由于

$ \{ t|\sum\limits_{s = t - \tau }^{t - 1} 1 \{ {I_s} = i\} < m\} = \{ t|{G_t}(\tau ,i) + {N_t}(\tau ,i) < m\} \supseteq \{ t|{\tau _{{\rm{max}}}} + {N_t}(\tau ,i) < m\} , $

有

$ \sum\limits_{t = K + 1}^T 1 \{ {I_t} = i,{\tau _{{\rm{max}}}} + {N_t}(\tau ,i) < m\} \le \left\lceil {T/\tau } \right\rceil m. $

令m=A(τ, i)+τ_max，得

$ \sum\limits_{t = K + 1}^T 1 \{ {I_t} = i \ne i_t^*,{N_t}(\tau ,i) < A(\tau ,i)\} \le \left\lceil {T/\tau } \right\rceil (A(\tau ,i) + {\tau _{{\rm{max}}}}). $

对于第2项，定义T(τ)为“卸载良好”的集合。数学上，其定义为：

$ {\mathscr{T}(\tau ): = \{ t|t \in \{ K + 1, \cdots ,T\} ;\mu _s^W(j) = \mu _t^W(j),} $

$ {\mu _s^P(j) = \mu _t^P(j),\forall s \in (t - C(\tau ),t),\forall j \in I\} ,} $

式中：C(τ)表示卸载时估计较差的任务的数目。特别地，令C(τ)=τ+τ_max。将这些估计较差的任务孤立出来，得到以下不等式

$ \sum\limits_{t = K + 1}^T 1 \{ {I_t} = i \ne i_t^*,{N_t}(\tau ,i) \ge A(\tau ,i)\} \le {Ƴ_T}(\tau + {\tau _{{\rm{max}}}}) + \sum\limits_{t \in \mathscr{T}(\tau )}^{} 1 \{ {I_t} = i \ne i_t^*,{N_t}(\tau ,i) \ge A(\tau ,i)\} . $

接下来，需要求得上式中最后一项的上界。注意到3个事实：

1) 事件{I_t=i≠i_t^*}发生当且仅当事件${\varepsilon _t}(\tau , i) = \left\{ {{{\bar U}_t}\left( {\tau , i_t^*} \right) - {c_t}\left( {\tau , i_t^*} \right) \ge {{\bar U}_t}(\tau , i) - {c_t}(\tau , i)} \right\}$发生；

2) ${\varepsilon _t}(\tau , i) \subseteq \left\{ {{{\bar U}_t}\left( {\tau , i_t^*} \right) - {c_t}\left( {\tau , i_t^*} \right) \ge {\mu _t}(i_t^*)} \right\} \cup \left\{ {{{\bar U}_t}(\tau , i) - {c_t}(\tau , i) < {\mu _t}(i_t^*)} \right\}$;

3) $\left\{ {{{\bar U}_t}(\tau , i) - {c_t}(\tau , i) < {\mu _t}(i_t^*)} \right\} \subseteq \left\{ {{{\bar U}_t}(\tau , i) - {c_t}(\tau , i) < {\mu _t}(i)} \right\} \cup \left\{ {{\mu _t}(i) - {\mu _t}(i_t^*) < 2{c_t}(\tau , i)} \right\}$.

基于以上事实，可得

$ \begin{array}{l} {I_t} = i \ne i_t^*,{N_t}(\tau ,i) \ge A(\tau ,i)\} \subseteq \{ {{\bar U}_t}(\tau ,i_t^*) - {c_t}(\tau ,i_t^*) \ge {\mu _t}(i_t^*)\} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \cup \{ {{\bar U}_t}(\tau ,i) + {c_t}(\tau ,i) < {\mu _t}(i)\} \cup \{ {\mu _t}(i) - {\mu _t}(i_t^*) < 2{c_t}(\tau ,i),{N_t}(\tau ,i) \ge A(\tau ,i)\} . \end{array} $

定义

$ \Delta {\mu _T}(i): = {\rm{mi}}{{\rm{n}}_{t \in \{ 1, \cdots ,T\} ,i_t^* \ne i}}{\mu _t}(i) - {\mu _t}(i_t^*). $

令A(τ, i):=4τ_max²ξlnτ(Δμ_T(i))^－2。若上述不等式中的事件{μ_t(i)－μ_t(i_t^*) < 2c_t(τ, i), N_t(τ, i)≥A(τ, i)}成立，则

$ \frac{{\Delta {\mu _T}(i)}}{2} = {\tau _{{\rm{max}}}}\sqrt {\frac{{\xi {\rm{ln}}\tau }}{{A(\tau ,i)}}} \ge {c_t}(\tau ,i). $

(A1)

然而，根据Δμ_t(i)的定义有

$ \frac{{\Delta {\mu _T}(i)}}{2} \le \frac{{{\mu _t}(i) - {\mu _t}(i_t^*)}}{2} < {c_t}(\tau ,i). $

(A2)

显然，式(A1)与式(A2)矛盾。因此事件{μ_t(i)－μ_t(i_t^*) < 2c_t(τ, i), N_t(τ, i)≥A(τ, i)}发生的概率为零。对于事件$\left\{ {{{\bar U}_t}\left( {\tau , i_t^*} \right) - {c_t}\left( {\tau , i_t^*} \right) \ge {\mu _t}(i_t^*)} \right\}$，有

$ \begin{array}{l} \mathbb{P}({\mu _t}(i) - {{\bar U}_t}(\tau ,i) > {c_t}(\tau ,i)) = \mathbb{P}\left( {{\mu _t}(i) - {{\bar U}_t}(\tau ,i) > {U_{{\rm{max}}}}\sqrt {\xi \frac{{{\rm{ln}}(t \wedge \tau )}}{{{N_t}(\tau ,i)}}} } \right)\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathop \le \limits^{(a)} \left\lceil {\frac{{{\rm{ln}}(t \wedge \tau )}}{{{\rm{ln}}(1 + \eta )}}} \right\rceil {\rm{exp}}\left( { - 2\xi {\rm{ln}}(t \wedge \tau )\left( {1 - \frac{{{\eta ^2}}}{{16}}} \right)} \right), \end{array} $

其中不等式(a)由文献[14]中的定理4得来。令$\eta : = 4\sqrt {1 - 1/(2\xi )} , \xi > 1/2$，得

$ \mathbb{P}({\mu _t}(i) - {\bar U_t}(\tau ,i) > {c_t}(\tau ,i)) \le \left\lceil {\frac{{{\rm{ln}}(t \wedge \tau )}}{{{\rm{ln}}(1 + \eta )}}} \right\rceil {(t \wedge \tau )^{ - 1}}. $

根据对称性，可知

$ \mathbb{P}({\bar U_t}(\tau ,i_t^*) - {c_t}(\tau ,i_t^*) \ge {\mu _t}(i_t^*)) = \mathbb{P}({\bar U_t}(\tau ,i) + {c_t}(\tau ,i) < {\mu _t}(i)). $

因此

$ \mathbb{E}[\sum\limits_{t = K + 1}^T 1 \{ {I_t} = i \ne i_t^*,{N_t}(\tau ,i) \ge A(\tau ,i)\} ] \le {Ƴ _T}(\tau + {\tau _{{\rm{max}}}}) + 2\sum\limits_{t \in \mathscr{T}(\tau )}^T {\left\lceil {\frac{{{\rm{ln}}(t \wedge \tau )}}{{{\rm{ln}}(1 + \eta )}}} \right\rceil {{(t \wedge \tau )}^{ - 1}}} . $

将所有相关项求和并作适当放缩可得

$ \mathbb{E}[{\tilde N_T}(i)] \le \frac{{T{\rm{ln}}\tau }}{\tau }B(\tau ) + {Ƴ _T}(\tau + {\tau _{{\rm{max}}}}) + \frac{{2{{({\rm{ln}}\tau )}^2} + 2{\rm{ln}}\tau }}{{{\rm{ln}}(1 + \eta )}}, $

其中

$ B(\tau ): = \left( {\frac{{4U_{{\rm{max}}}^2\xi }}{{{{(\Delta {\mu _T}(i))}^2}}} + {\tau _{{\rm{max}}}}} \right)\frac{{\left\lceil {T/\tau } \right\rceil }}{{T/\tau }} + 2\frac{{\left\lceil {\frac{{{\rm{ln}}\tau }}{{{\rm{ln}}(1 + \eta )}}} \right\rceil }}{{{\rm{ln}}\tau }}. $

证毕。