2. 国网浙江省电力有限公司, 杭州 310007;
3. 中国科学院大学, 北京 100049;
4. 上海科技大学, 上海 201210;
5. 上海雾计算实验室, 上海 201210
2. State Grid Zhejiang Power Co Ltd, Hangzhou 310007, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China;
4. ShanghaiTech University, Shanghai 201210, China;
5. Shanghai Institute of Fog Computing Technology, Shanghai 201210, China
随着智能物联网、5G与人工智能等技术的兴起与发展,处理海量且多样性的数据、满足超低的服务时延需求,成为越来越亟待解决的问题[1]。传统的基于集中式的云计算架构由于终端设备与云服务器的遥远距离而产生较大时延,已难以满足时延敏感性服务的需求;同时,基于集中式的管理也难以支撑海量设备的接入。在这种情况下,雾计算(fog computing)[2]应运而生。雾计算技术将通信、计算、控制和存储等能力从云端推向网络边缘(如(小)基站、无线接入点及其他有计算能力的终端设备)[3],通过资源共享机制和协同服务架构帮助资源有限的移动设备执行具有超低延迟限制的计算密集型应用程序,从而有效提升用户体验或者生产效率,有望成为支撑未来智能物联网、5G和人工智能应用的关键技术[4-5],受到广泛的关注与研究。
任务卸载(task offloading)是雾计算的主要技术之一,计算资源有限的节点在难以独立支持应用服务时,可将计算任务卸载到网络中资源充足的节点帮助计算。需要进行任务卸载的节点叫做任务节点(task node),提供计算帮助的节点叫做帮助节点(help node)。时延和能耗是任务卸载过程中两个重要的指标,有大量学者对其进行了研究[2-11],本文主要考虑时延。
一方面,目前大多数学者考虑的都是静态网络里的任务卸载,即在任务卸载过程中,网络中的移动设备处于静止状态,且帮助节点所提供的计算资源保持不变[6-7]。在文献[6]的研究模型里,终端设备可以通过基站将任务卸载给附近的云,为多设备的任务卸载场景提出一种基于博弈论的任务卸载算法。Dinh等[7]通过联合优化任务分配和节点的计算频率,最小化时延和能量总消耗。然而在实际中,任务节点和帮助节点往往都不是静止的,而是处在移动状态,经历着多变的无线信道;并且,帮助节点可提供的计算资源也可能发生变化。
另一方面,现有的研究大都假设系统中的节点状态信息已知,或者这些信息可以实时广播到网络中[8-9]。由于任务的卸载决策通常需要帮助节点状态相关信息,比如任务队列长度、可共享资源大小等,因此任务卸载过程本身便可看作典型的随机决策过程。对此,许多研究工作利用李亚普诺夫优化(Lyapunov optimization)等方法解决这种随机决策问题,从而实现任务或计算资源的近似最优分配[8-9]。不停在网络中广播及监听节点的状态信息会产生大量的能量开销,影响设备使用时长,在未来超大规模体系中,节点个数倍数增加的场景下,这个问题将更加突出。
为减少由于多次沟通信息导致的能量损耗,基于学习(learning)的方法被提出[10]。文献[10]使用马尔可夫决策方法动态地进行服务资源的配置和卸载决策。Tan等[11]为雾计算网络设计基于学习的任务卸载算法,但未建模考虑任务的排队情况,此外,该工作也未考虑任务本身的时延需求,可能过多地导致任务不满足时延需求。
在实际情况中,节点会动态出入网络,帮助节点可共享的计算资源也会随情况发生变化;同时,实时在网络中传输或广播节点状态信息又会造成大量的能量开销。这样一个最贴近实际需求又有待解决的问题,却鲜有学者研究。本文旨在为这样的动态雾计算网络设计任务卸载算法,最优化设备的任务卸载时延,同时尽量满足其任务时延需求,任务节点无需实时请求网络中帮助节点的状态信息,如队列信息及计算资源信息等,而是以很小的计算代价根据自己的历史卸载经验学习和判断得来。本文动态雾计算网络中的“动态”有3个含义:1)网络中的节点运动状态可变;2)网络大小可变:节点可自由出入网络;3)帮助节点可提供的计算资源可变。
本文首先为稳定状态下的动态网络提出任务卸载算法TOD(online learning-based task offloading algorithm for the dynamic fog networks under stationary status)。在稳定状态里,网络中节点的参数达到稳定。稳定状态一般适用于以下场景:节点静止或缓慢移动,可自由出入网络,帮助节点可提供稳定的计算资源。接着,扩展TOD算法到非稳定网络状态下,提出TOD-N算法(online learning-based task offloading algorithm for the dynamic fog networks under non-stationary status),以动态追踪网络中变化的最优资源和节点。在非稳定环境中,系统参数会随着时间而变化。非稳定状态可能包含有以下场景:节点(快速)移动,可自由出入网络,信道环境变化较大,帮助节点可提供计算资源随时间改变。然后,针对所提出的两个算法进行详细的性能分析,包括算法与理想算法的近似情况、算法复杂度分析以及存储空间占用分析等。仿真结果表明,本文算法所能达到的卸载时延与理想情况下的最优卸载时延十分相近,且任务卸载服务的时延满足率显著提升;此外,TOD-N算法在非稳定的网络状态下能够追踪计算资源与环境的变化,与贪心(Greedy)算法相比,性能显著提升。
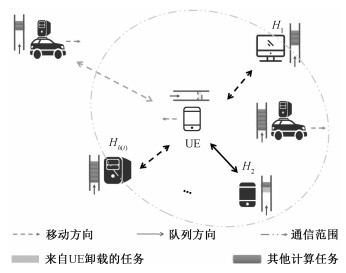
1 系统模型与问题建模 1.1 系统模型与目标本文考虑单对多(单个任务节点,多个帮助节点)任务卸载,且任务不可拆分的情况,即一个任务节点可从多个帮助节点中选择一个来卸载任务。将时间划分为若干个时隙,假设从时隙t=0开始,UE在每个时隙的开始产生一个卸载请求Rt,表示为Rt={xt, Δt},其中xt为Rt任务大小,Δt表示任务Rt可容忍的最大时延。通常,由于返回的结果很小(几到几十个比特),结果的返回时延可忽略不计[3]。每当有卸载请求时,UE从愿意共享计算资源的候选帮助节点里选择一个来完成任务卸载。将t时隙里UE的候选节点表示为集合H(t),H(t)={H1, H2, …, HH(t)},其中h(t)=|H(t)|。由于UE不能实时掌握或请求网络中帮助节点的节点状态信息,因此,UE需要根据自己的历史卸载数据等对当前帮助节点Hk∈H(t)进行学习,以便找到优秀的帮助节点进行任务卸载。如图 1所示,UE选择H2卸载任务Rt。
|
Download:
|
| 图 1 t时隙下的动态雾网络图示 Fig. 1 Illustration of the dynamic fog network at time t | |
本文以最小化平均任务卸载时延、提高任务卸载成功率为目标设计任务卸载算法。任务的卸载时延包含3个部分[3]:传输时延、等待时延和计算时延。
UE将Rt发送到Hk的传输时延为Dkt(t),且
| $ D_k^t(t) = {x_t}/{r_k}(t). $ | (1) |
式中rk(t)为UE到Hk的传输速率,根据香农公式可得
| $ {r_k}(t) = B{\rm{lo}}{{\rm{g}}_2}\left( {1 + \frac{{{P_k}(t){g_k}(t)}}{{{N_0}(t)}}} \right). $ | (2) |
式中:Pk(t)为发射功率,gk(t)为信道增益,N0(t)为噪声功率。任务Rt到达Hk便进入队列等待处理,Hk的队列长度表示为Xkq(t),假设Hk的服务模式为先进先出(FIFO),则Rt的等待时延为
| $ D_k^w(t) = X_k^q(t)X_k^e(t). $ | (3) |
式中:Xke(t)为Hk在时间t处理单位任务的时延,服从指数分布。指数分布被广泛用于建模移动计算任务的时延[2]。Xke(t)在不同节点之间以及同一节点不同时间之间均分布独立。Hk处理Rt的时延为
| $ D_k^e(t) = X_k^e(t){x_t}. $ | (4) |
最终,UE将Rt卸载到Hk的卸载服务时延可表示为
| $ {D_k}(t) = D_k^t(t) + D_k^e(t) + D_k^w(t). $ | (5) |
令Π表示在从t=1到t=T所有可能的卸载策略,则直到t=T为止,UE的任务平均卸载时延为
| $ {P_0}:{\rm{mi}}{{\rm{n}}_{\phi \in \Pi }}{\rm{E}}\left[ {\frac{1}{T}\sum\limits_{t = 1}^T {{D_{\phi (t)}}} (t)} \right]. $ | (6) |
式中:ϕ(t)=k表示UE选择Hk卸载Rt。由于UE不能实时请求帮助节点状态信息,也就是说在式(6)中,Xkq(t)和Xke(t)都是未知的,需要UE对其进行学习,才能做出卸载判断。
若任务Rt的实际卸载服务时延小于或等于其可容忍时延Δt,则认为该次任务卸载是成功的。令Iks(t)=1表示任务Rt卸载成功,否则Iks(t)=0。令Δmax=maxtΔt。
1.2 将原模型建模为MAB问题由于Xkq(t)和Xke(t)均未知,且问题P0需要实时的决策,可将其看作在线优化问题。本文将原系统问题P0转换为MAB (multi-armed bandit)问题[12],再设计算法求解。MAB问题是经典的在线学习问题,同时也是简单的强化学习问题。P0在对应的MAB问题中,UE为代理人,帮助节点Hk∈H(t)为在时间t可选的臂(arm)。则原任务卸载问题可解读为:UE在每个时隙的开始,根据历史的任务卸载经验及当前任务的时延容忍情况做出决策ϕ(t),并获得即时反馈Xϕ(t)q(t)与Xϕ(t)e(t),实际任务卸载时延将在任务卸载服务完成后知晓。UE需要找到最优策略ϕ*最小化累计时延。通过以上分析,P0转换为设计一个在线随机优化算法解决如下优化问题:
| $ \begin{array}{*{20}{l}} {{P_1}:\mathop {{\rm{min}}}\limits_{\phi \in \Pi } \frac{1}{T}{\rm{E}}[\sum\limits_{k = 1}^{{\varphi _T}} {\sum\limits_{s = 1}^{N_k^\phi (T)} {{D_k}} } (s)], }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{s}}{\rm{.t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{k = 1}^{{\varphi _T}} {N_k^\phi } (T) = T, }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} N_k^\phi (T) \in \mathbb{N}, \forall k \in {\Psi _T}.} \end{array} $ | (7) |
式中:Nkϕ(t)表示采用策略ϕ∈Π后,直到时间T为止Hk被选择过的次数; ΨT={H1, H2, …, Hφt}表示直到时间T为止,所有共享过计算资源的帮助节点的集合,且φT=|ΨT|。
与传统的MAB问题相比,本文的研究问题有如下挑战:1)传统的MAB问题动作空间恒定,本文由于节点移动出入网络或是否愿意继续共享资源,使问题具有动态变化的动作空间,更加复杂。2)传统MAB问题中通常系统参数稳定,如某个动作的平均收益稳定,本文中节点的自由移动、信道环境变化,以及共享计算资源的变化,可能导致系统参数实时发生变化。
2 基于UCB的在线任务卸载算法本文考虑任务本身的时延需求,在上节所述的2个挑战下,基于UCB(upper confidence bound)[13]提出在线任务卸载算法解决问题P1。首先提出TOD算法,适用于节点的参数稳定,处在稳定状态下的雾计算网络。由于帮助节点可共享的计算资源可能随着时间发生变化,节点的任务队列信息也可能会发生一系列改变,在这种情况下,节点处理单位任务的时延会相应发生变化。为应对和处理这些情况,将算法TOD进行扩展,为处在非稳定状态的雾计算网络提出TOD-N算法。值得注意的是,TOD算法与TOD-N算法并不对系统参数分布做出限制。
2.1 稳定网络状态下的任务卸载算法稳定状态下,系统参数的统计特征稳定,令Ε(Xkq(t))=Qk,E[Xke(t)]=uke,E[Dk(t)]=uk(t),则uk(t)=Qkuke+xt/rk(t)+xtuke。算法TOD的伪代码如算法1所示。
|
|
UE根据为Hk分配的索引值
| $ {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over u} _k}(t) = {Q_k}\bar u_k^e + {x_t}/{r_k}(t) + {x_t}\bar u_k^e - {c_k}(t). $ | (8) |
式中:
| $ {\bar u_k^e = 1/{N_k}(t)\sum\limits_{s = 1}^t {X_k^e} (t){I^\phi }\{ \phi (s) = k\} , } $ | (9) |
| $ {{{\bar Q}_k} = 1/{N_k}(t)\sum\limits_{s = 1}^t {X_k^q} (t){I^\phi }\{ \phi (s) = k\} .} $ | (10) |
式中:
| $ {c_k}(t) = {\varDelta _{{\rm{max}}}}\sqrt {\zeta \tau ({\Delta _t}){\rm{log}}(\Gamma _k^a(t))/{N_k}(t)} . $ | (11) |
式中:ζ为常量;Γka(t)表示直到t为止Hk参与资源共享的总时间,
由于可共享计算资源的变化以及信道环境等变化,网络节点状态可能会处在非稳定状态下,参数可能会变化,此时系统参数的统计特征不再稳定,uke和Qk不再恒定。此时令Qk(t)=E[Xkq(t)],uke(t)=E[Xke(t)]。在非稳定状态下,最优决策也可能会随时发生变化,因此算法的设计要能跟踪到这种变化,才能找到最优的帮助节点。本节将TOD算法升级为TOD-N算法,通过引入参数γ∈(0, 1],对历史数据分配不同权重,实现越新的历史数据对当前决策的影响越大,而越旧的历史数据则影响越小。TOD-N算法在做出决策前为当前候选帮助节点Hk∈H(t)分配索引
| $ \begin{array}{*{20}{l}} {\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}} \over u} _k^n(t, \gamma ) = {{\bar Q}_k}(t, \gamma )\bar u_k^e(t, \gamma ) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {x_t}/{r_k}(t) + {x_t}\bar u_k^e(t, \gamma ) - c_k^n(t).} \end{array} $ | (12) |
式中:
| $ \bar u_k^e(t, \gamma ) = 1/N_k^n(t, \gamma )\sum\limits_{s = 1}^{t - 1} {{\gamma ^{t - s}}} X_k^e(t){I^\mathit{\boldsymbol{\phi}} }\{ \mathit{\boldsymbol{\phi}} (s) = k\} , $ | (13) |
| $ {\bar Q_k}(t, \gamma ) = 1/N_k^n(t, \gamma )\sum\limits_{s = 1}^{t - 1} {{\gamma ^{t - s}}} X_k^q(t){I^\mathit{\boldsymbol{\phi}} }\{ \mathit{\boldsymbol{\phi}} (s) = k\} . $ | (14) |
式中:Nkn(t, γ)与ckn(t)分别为Nk(t)与ck(t)在非稳定环境下的表示,且
| $ {N_k^n(t, \gamma ) = \sum\limits_{s = 1}^{t - 1} {{\gamma ^{t - s}}} {I^\mathit{\boldsymbol{\phi}} }\{ \mathit{\boldsymbol{\phi}} (s) = k\} , } $ | (15) |
| $ {c_k^n(t) = 2{\varDelta _{{\rm{max}}}}\sqrt {\zeta \tau ({\varDelta _t}){\rm{log}}(\Gamma _k^a(t, \gamma ))/N_k^n(t, \gamma )} .} $ | (16) |
TOD-N算法的伪代码如算法2所示。
|
|
本节将对TOD算法、TOD-N算法进行性能分析,包括算法的最优近似情况、算法的计算复杂度以及内存占用情况。
本文使用学习遗憾(learning regret)分析TOD算法与TOD-D算法的最优近似情况。Regret分析被广泛用于分析在线学习算法性能的文献中[14],它衡量所提出算法与最优算法之间的差距。为了分析有动态动作空间的在线决策问题,将时间看作时段的组合,在一个时段内,没有新的动作产生,即没有新的帮助节点加入,令ps={sa, …, sb}表示时段s,sa与sb分别为时段ps的起止时间,显然ts=sb-sa≤T。PT表示直到时间T为止,拥有的时段个数,
| $ {R^\mathit{\boldsymbol{\phi}} }(T) = \sum\limits_{i = 1}^T {{D_{\mathit{\boldsymbol{\phi}} (t)}}} (t) - {u_{{k^*}(t)}}(t). $ | (17) |
令Δmax=maxtΔt,则当ϕ=TOD时, 有如下结论:
结论1 若动态调整Δ+和Δ-,使得∀t,τ(Rt)=1,则
| $ {\rm{lim}}\mathop {{\rm{sup}}}\limits_{T \to \infty } \frac{{{R^{{\rm{TOD}}}}(T)}}{{{\rm{log}}(T)}} \le 8{\Delta _{{\rm{max}}}}\sum\limits_{s = 1}^{{P_T}} {\sum\limits_{k \ne k_s^*} {\frac{1}{{{d_{k, k_s^*}}}}} } + O(1), $ |
式中:dk, ks*=(uk-uks*)/Δmax,
从结论1发现,RTOD(T)随PT增长线性增长。特别地,若PT=1,即网络中帮助节点个数稳定不变,此时可得
假设uke(t)与Qk(t)随时间t平滑地变化。也就是说,uke(t)与Qk(t)均为时间t的利普西茨函数,且存在σ,∀t, t′,max{|uke(t)-uke(t′)|, |Qk(t)-Qk(t′)|}≤σ|t-t′|。由于最优决策会随着时间变化,两个帮助节点可能会具有过近的卸载时延,由此导致算法决策失误。定义ωs为时段ps里其他决策和最优决策距离小于ε(ε>0)的时间集合:ωs={t∈ps||ukn(t)-uk*(t)n(t) < ε}。令χs=ωs,且约束χs≤Cδ(γ, σ)εts,其中C为衡量时间比例的常量,δ(γ, σ)=(σ2+σ)γ反映网络中节点状态的变化情况。令
结论2 令
| $ N_k^s \le {\chi _s} + ({s_b} - {s_a})A(\gamma )(1 - \gamma ){\rm{log}}(\frac{\gamma }{{1 - \gamma }}). $ |
式中:
证明见附录B。
结论2表明,Nks由χs及γ的选择共同决定。根据类似于文献[15]的分析,为了使TOD-N算法拥有良好性能,要尽可能降低TOD-N选择非最优节点的次数,也就是要降低Nks。χs由外部环境决定,因此只能调节参数γ最小化Nks,结合结论2可得
| $ \gamma = 1 - {(4{\varDelta _{{\rm{max}}}})^{ - 1}}\sqrt {{\chi _s}/T} . $ | (18) |
由式(18)发现,在某时段ps里,若系统不稳定性增加,则χs变大,那么γ的值选择应当减小。这个结论与直观上的理解相符合:若系统参数变化较大,则当前决策与较近卸载数据关系较大,而与较远卸载数据几乎没有关系。令RsTOD-NTOD-N算法在时段ps的学习Regret,则有:
结论3 当ϕ=TOD-N,存在常数C′, 使得下式成立
| $ R_s^{{\rm{TOD - N}}}/{t_s} \le {C^\prime }{\Delta _{{\rm{max}}}}\sum\limits_{{H_k} \in {H_p}} {\sqrt {{t_s}{\chi _s}} } {\rm{log}}{t_s}. $ | (19) |
证明见附录C。
结论3表明,若χs→0, 则RTOD-N/ts→0。也就说明, 当最优决策发生变化的次数越少, 算法单次决策的Regret越小; 且当σ→0,即uke(t)与Qk(t)变化越缓慢时,算法单次决策的Regret越小,也就能更好地追踪到网络中的最优帮助节点。
3.2 算法复杂度及内存占用情况分析在网络中存在K个帮助节点时,UE采用TOD算法和TOD-N算法做出卸载决策的算法复杂度均为O(KlogK)。此外,当ϕ=TOD-N时,采用如下方式更新维护Nkn(t, γ),ukn(t, γ)与Qkn(t, γ),将大大减少内存占用,
| $ N_k^n(t, \gamma ) = \gamma N_k^n(t, \gamma ) + \gamma {I^\phi }\{ \phi (t) = k\} , $ | (20) |
| $ u_k^n(t, \gamma ) = 1/N_k^n(t, \gamma )\left( {\begin{array}{*{20}{l}} {\gamma N_k^n(t - 1, \gamma )u_k^n(t - 1) + }\\ {\gamma X_k^e(t){I^\phi }\{ \phi (t) = k\} } \end{array}} \right), $ | (21) |
| $ Q_k^n(t, \gamma ) = 1/N_k^n(t, \gamma )\left( {\begin{array}{*{20}{l}} {\gamma N_k^n(t - 1, \gamma )Q_k^n(t - 1) + }\\ {\gamma X_k^q(t){I^\phi }\{ \phi (t) = k\} } \end{array}} \right). $ | (22) |
本节对TOD算法以及TOD-N算法进行性能仿真验证。主要考察采用所提出算法后的任务卸载的时延情况、任务卸载成功率以及算法的学习性能。
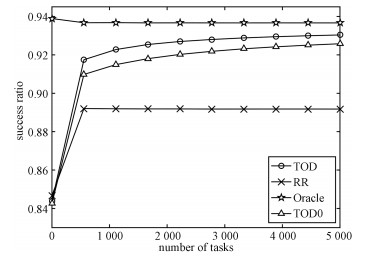
4.1 TOD算法仿真结果首先检验TOD算法对任务时延需求的满足情况。图 2给出在网络状态稳定且网络大小一定时,任务卸载的成功情况。仿真中网络里有8个候选帮助节点,k=1, …, 8。时隙长度为20 ms。ζ=0.6,Δ+=6e-6,Δ-=0。xt(单位:Mbit)服从均匀分布,且∀t,xt~U(0.4, 0.6)。∀t, Δt(单位:s)有:Δt/xt~U(1.3e-6, 1.5e-6)。单位任务大小x0为1 Byte。∀k,Xke~exp(uke),Xkq~U(ak, bk)。ue=[uke]k=1, …, 8,ue=[0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8],a=[ak]k=1, …,8,a=[4.1, 1.6, 0.6, 0.4, 0.25, 0.105, 0.06, 0.015],b=[bk]k=1, …, 8,b=[3.9, 1.4, 0.4, 0.2, 0.15, 0.095, 0.05, 0.005]。无线资源调度[16]以及功率控制优化[17]不是本文考虑的重点,因此本节假设∀k, rk=24 Mbit/s。图 2所示为5 000次实验的平均值。
|
Download:
|
| 图 2 稳定网络状态下不同算法的任务卸载成功情况 Fig. 2 Task offloading success ratios for different algorithms under stationary status | |
图 2中RR算法为轮询调度(round-robin)算法,轮流选择帮助节点进行任务卸载。Oracle算法表示理想算法,UE实时地对帮助节点处的排队情况、计算资源情况以及信道环境情况了如指掌,这在实际中是不现实的。当调节Δ+和Δ-使τ(Rt)始终为1的时候,TOD就变成TOD0算法,注意到此时相当于TOD0算法未考虑任务本身的时延需求。从图 2可以看出,相比RL算法与TOD0算法,TOD算法能够有效地提升任务卸载的成功率,所达到的累计概率和Oracle算法十分接近,且随着任务卸载次数增加,卸载成功率也会越来越靠近理想状态下的任务卸载成功率。
图 3所示为TOD算法在网络中有节点自由出入时的性能表现。时隙长度为20 ms。∀t,xt=x,图 3中有两种输入任务大小,分别为x=0.5 Mbit和x=0.8 Mbit。∀k, rk=48 Mbit/s。仿真过程中有3个等长时段:T1,T2和T3,长度分别为5 s。节点在网络中的存在情况如表 1所示,此时,ue,a和b分别为:ue=[0.08, 0.2, 0.2, 0.4, 0.5, 0.5, 0.7, 0.8],a=[3.1, 1.6, 0.6, 0.4, 0.25, 0.007, 0.06, 0.015],b=[2.9, 1.4, 0.4, 0.2, 0.15, 0.005, 0.05, 0.005]。

|
Download:
|
| 图 3 TOD算法在稳定状态下的时延表现 Fig. 3 Average offloading delays under stationary status by TOD algorithm | |
|
|
表 1 TOD算法候选帮助节点 Table 1 Candidate help nodes by TOD algorithm |
从图 3可以看出,在网络动态变化后,TOD算法能快速找到新的最优帮助节点,且采用TOD算法的时延与理想算法的时延十分接近。进一步对比时段1与时段2发现,两种大小的任务平均时延差距变小,这是因为帮助节点的队列长度不同,因此当任务大小不同时,相应的最优节点可能不同。
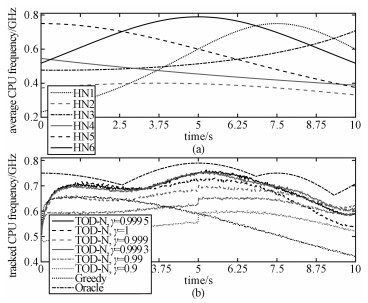
4.2 TOD-N算法仿真结果接下来检验算法在非稳定网络状态下的表现。仿真过程中共出现过6个帮助节点,各个帮助节点可提供的共享计算资源随时间改变,如图 4(a)所示。时隙长度为20 ms。仿真过程可分为两个时段:T1和T2,长度各为5 s,各节点在各时段的存在情况如表 2所示。∀t,xt=0.6 Mbit。参考文献[7],任务的计算密度设置为330 Cycls/bit。∀k,∀t,Qk(t)(单位:Mbit)有:Qk(t)~U(0.25,0.35),且Δt(单位:s)有:Δt/xt~U(1.3e-6, 1.5e-6),Δ+=6e-6,Δ-=0。此外,为了体现出算法对网络中节点计算资源的学习情况,需要尽量减少传输试验带来的影响,因此假设∀k, rk=72 Mbit/s。本节将TOD-N算法与Greedy算法和理想Oracle算法进行对比。Greedy算法每次决策时均选择目前的最优节点,Oracle算法则依然实时地对所有帮助节点的排队情况、计算资源情况等了如指掌。同时,为进一步分析Γ参数对算法性能的影响,本节给出TOD-N算法在不同Γ值下的性能表现。根据图 4(a),最优节点和次优节点不可分的时隙个数在T1和T2时段分别为1和2,根据式(18)可得,相应的参数γ分别为0.999 5和0.999 3。实验中另外给出的实验数据值分别为γ=1,0.999,0.99,0.9。TOD-N算法在非稳定网络状态下的性能表现如图 4~图 6所示。
|
Download:
|
| 图 4 不同算法对网络中最优计算资源的追踪情况 Fig. 4 Learning performance on computing resource for different algorithms | |
|
|
表 2 TOD-N算法候选帮助节点 Table 2 Candidate help nodes by TOD-N algorithm |
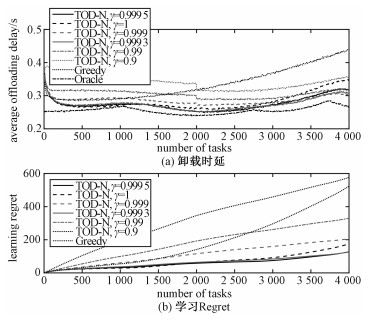
|
Download:
|
| 图 5 不同算法下的卸载时延及学习Regret Fig. 5 Average offloading delays and learning regrets for different algorithms | |
|
Download:
|
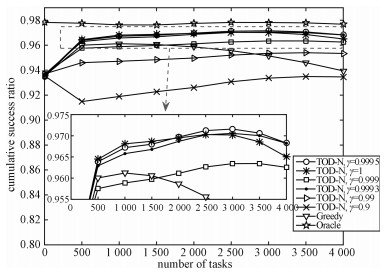
| 图 6 非稳定网络状态下不同算法的任务卸载成功情况 Fig. 6 Task offloading success ratios for different algorithms under non-stationary status | |
图 4(b)为TOD-N算法对网络中计算资源的学习追踪与利用情况,结合图 4(a)、4(b)可以看出,当γ=0.999 5和0.999 3时,TOD-N算法均能较好地追踪学习到最佳CPU资源,Greedy算法则无法做到。进一步地,可发现,当γ=1和0.999时,TOD-N总体表现比前两个值要逊色一些,但在某些局部时段里表现却要好一些。例如,在刚开始的一段时间里γ=1要比γ=0.999 3时性能好一些,在最后一段时间里γ=0.999要比γ=0.999 5稍微好一点。这是因为刚开始网络状态相对较稳定,因此γ选择大一些;在最后一段时间里,网络状态变化相对较快,因此γ选择可相对减小一些。以上结论与3.1.2节分析的结论一致。但当γ=0.99,甚至γ=0.9,TOD-N算法无法很好地适应非稳定网络状态,同时,图 5(b)也同时表明,此时Regret增长很快,算法表现较差。这是因为γ值选择过小的话,算法基本丢掉了历史有用的数据信息,而过于依赖当前的数据。根据以上分析发现,参数γ的选择确实会对TOD-N算法性能造成影响,具体选择可参考式(18)。但是在实际情况中,很难提前知道网络情况,因此很难实时地对γ做出最优判断,但是如图 4~图 6所示,根据实验结果与分析,本文建议选用γ∈(0.99, 1),在这个范围内,均可有较为良好的结果,具体值可结合实际情况做出调整。
图 5(a)表明,当合理选择γ,TOD-N在非稳定状态下可达到的时延和理想最优时延十分接近,可达5 ms以内,同时从图 6可知,此时任务卸载成功率也明显比贪心算法高,且与最优成功率之差在1%以内。
5 总结本文将动态雾计算网络中的任务卸载问题建模为具有动态动作空间的MAB问题,并为稳定状态雾网络提出基于在线学习的任务卸载算法TOD,该算法能够最优化平均卸载时延,并提高任务卸载成功率。再将TOD扩展到非稳定网络状态情况,提出TOD-N算法,TOD-N算法能动态追踪到网络中节点的计算资源。接着对TOD算法和TOD-N算法进行详细的性能分析。并同时对TOD-N中的参数γ进行一定讨论和实验。仿真结果验证了所提出算法的优异性能。未来将进一步考虑任务可拆分以及节点之间可协作的场景。
附录A根据式(17)的定义,当ϕ=TOD,RTOD(T)可写作
| $ {R^{{\rm{TOD}}}}(T) = \sum\limits_{s = 1}^{{P_T}} {{R_s}} . $ | (A.1) |
式中:
| $ {R_s} = {\varDelta _{{\rm{max}}}}{\rm{E}}{\left[ {\sum\limits_{t \in {p_s}} {\frac{{{u_{\pi (t)}}(t)}}{{{\varDelta _{{\rm{max}}}}}}} - \frac{{{u_{k_s^*}}(t)}}{{{\varDelta _{{\rm{max}}}}}}} \right]_s}. $ | (A.2) |
令Γks与Nks分别表示Hk在时段ps内处于活跃状态的总时间及其被选择的次数,dk, ks*=(uk-uks*)/(Δmax)。则
| $ {R_s} = {\varDelta _{{\rm{max}}}}\sum\limits_{k \ne {k^*}} {{d_{k, k_s^*}}} {\rm{E}}[N_k^s]. $ | (A.3) |
当单位任务容忍时延一定时,即∀t,Δt/xt=Δ0,令Δ+=Δ0,Δ-=0,则∀t,τ(Rt)=1。根据文献[11]的定理1以及文献[15]的引理1可得
| $ {\rm{E}}[N_k^s] \le 8{\rm{log}}({\Gamma _k})/{d_{k, k_s^*}} + (1 + \pi /3). $ | (A.4) |
显然Γk≤ts≤T,结合式(A.1)(A.3)(A.4)则可得到结论1。
附录B令
| $ \begin{array}{l} N_k^{n, s} = \sum\limits_{t \in {p_s}} 1 \{ \mathit{\boldsymbol{\phi}} (t) = k \ne {k^*}(t)\} = \sum\limits_{t \in {p_s}} 1 \{ \mathit{\boldsymbol{\phi}} (t) = k \ne {k^*}(t), N_k^n(\gamma , t) < \iota (\gamma , \sigma )\} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{t \in {p_s}} 1 \{ \mathit{\boldsymbol{\phi}} (t) = k \ne {k^*}(t), N_k^n(\gamma , t) \ge \iota (\gamma , \sigma )\} \le \left\lceil {{t_s}(1 - \gamma )} \right\rceil (\gamma , \sigma ){\gamma ^{ - 1/(1 - \gamma )}} + \sum\limits_{t \in {p_s}} {{\Theta _k}} (t). \end{array} $ | (B.1) |
式中:Θk(t)=1{ϕ(t)=k≠k*(t), Nkn(γ, t)≥ι(γ, σ)},最后一个不等号的成立是依据文献[14]的推论1。根据本文中3.2.2节定义,
| $ {\Theta _k}(t) \le {\chi _s} + \sum\limits_{t \in {{\bar \omega }_s}} 1 \{ \mathit{\boldsymbol{\phi}} (t) = k \ne {k^*}(t), N_k^n(\gamma , t) \ge \iota (\gamma , \sigma )\} . $ | (B.2) |
式(B.2)中事件{ϕ(t)=k≠k*(t)}意味着下式成立:
| $ \{ \bar u_{{k^*}(t)}^n(\gamma , t) - c_{{k^*}(t)}^n(\gamma , t) \ge \bar u_k^n(\gamma , t) + c_k^n(\gamma , t)\} . $ |
对{ϕ(t)=k≠k*(t)}有
| $ \begin{array}{*{20}{l}} {\{ \mathit{\boldsymbol{\phi}} (t) = k \ne {k^*}(t)\} \subseteq \{ {u_k}(t) - {u_{{k^*}(t)}}(t) < 2c_k^n(\gamma , t)\} }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \cup \{ \bar u_{{k^*}(t)}^n(\gamma , t) - c_{{k^*}(t)}^n(\gamma , t) \ge {u_{{k^*}(t)}}(t)\} \cup \{ \bar u_k^n(\gamma , t) + c_k^n(\gamma , t) \le {u_k}(t)\} .} \end{array} $ | (B.3) |
此时,可得
| $ \begin{array}{*{20}{l}} {{\Theta _k}(t) \le \{ {u_k}(t) - {u_{{k^*}(t)}}(t) < 2c_k^n(\gamma , t), N_k^n(\gamma , t) \ge \iota (\gamma , \sigma )\} }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \cup \{ \bar u_{{k^*}(t)}^n(\gamma , t) - c_{{k^*}(t)}^n(\gamma , t) \ge {u_{{k^*}(t)}}(t)\} \cup \{ \bar u_k^n(\gamma , t) + c_k^n(\gamma , t) \le {u_k}(t)\} .} \end{array} $ | (B.4) |
则根据定义,当
| $ {u_k}(t) - {u_{{k^*}(t)}}(t) - 2c_k^n(\gamma , t) \ge \varepsilon - 2c_k^n(\gamma , t) \ge 0, $ | (B.5) |
则{uk(t)-uk*(t)(t) < 2ckn(γ, t), Nkn(γ, t)≥ι(γ, σ)}不会发生。为了进一步推导Θk(t),定义Mkn(γ, t)和Skn(γ, t):
| $ {\Xi _1} = |M_k^n(\gamma , t) - u_k^n(t)N_k^n(\gamma , t)| \le {\varDelta _{{\rm{max}}}}. $ | (B.6) |
其次,对于
| $ \begin{array}{*{20}{l}} {{\Xi _1} = |\sum\limits_{s = 1}^{t - {X_s}} {{\gamma ^{t - s}}} ({u_k}(s) - {u_k}(t))1\{ \mathit{\boldsymbol{\phi}} (s) = k\} | \le \sum\limits_{s = 1}^{t - {X_s}} {{\gamma ^{t - s}}} |{u_k}(s) - {u_k}(t)|1\{ \mathit{\boldsymbol{\phi}} (s) = k\} }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \le {\varDelta _{{\rm{max}}}}\sum\limits_{s = 1}^{t - {\chi _s}} {{\gamma ^{t - s}}} 1\{ \mathit{\boldsymbol{\phi}} (s) = k\} \le {\varDelta _{{\rm{max}}}}{\gamma ^\chi }{{(1 - \gamma )}^{ - 1}}.} \end{array} $ | (B.7) |
若χs≥logγ(1-γ)ζlog(Γkn(t, γ)),结合式(B.6)(B.7)得
| $ {\Xi _1} \le {\rm{min}}\{ {\varDelta _{{\rm{max}}}}, {\varDelta _{{\rm{max}}}}{\gamma ^{{\chi _s}}}{(1 - \gamma )^{ - 1}}\} \le {\varDelta _{{\rm{max}}}}\sqrt {{\gamma ^\chi }{{(1 - \gamma )}^{ - 1}}N_k^s{{(\gamma , t)}^{ - 1}}} \le 1/2c_k^n(\gamma , t). $ | (B.8) |
令
| $ \begin{array}{l} {\Xi _2} \le P\left\{ {\begin{array}{*{20}{l}} {u_k^n(t) - \bar u_k^n(\gamma , t) > + |M_k^n(\gamma , t)/N_k^n(\gamma , t) - u_k^n(t)|}\\ { + {\varDelta _{{\rm{max}}}}\sqrt {\zeta {\rm{log}}(\Gamma _k^a(\gamma , t))/N_k^n(\gamma , t)} } \end{array}} \right\} \le P\left\{ {\begin{array}{*{20}{l}} {(M_k^n(\gamma , t) - S_k^n(\gamma , t))/\sqrt {N_k^n({\gamma ^2}, t)} }\\ { \ge {\varDelta _{{\rm{max}}}}\sqrt {\zeta {\rm{log}}(\Gamma _k^a(t, t))/N_k^n({\gamma ^2}, t)} } \end{array}} \right\}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \le \left\lceil {{\rm{log}}(\Gamma _k^a(\gamma , t)){{({\rm{log}}(1 + \eta ))}^{ - 1}}} \right\rceil \Gamma _k^a{(\gamma , t)^{ - \zeta (2 - {\eta ^2}/8)}} \end{array} $ | (B.9) |
最后一个不等式的成立是依据文献[15]的定理4。当
| $ \begin{array}{*{20}{l}} {\sum\limits_{t \in {{\bar \omega }_s}} {{\Xi _2}} = \sum\limits_{t \in {{\bar \omega }_s}} {\left\lceil {\log (\Gamma _k^a(\gamma , t)){{({\rm{log}}(1 + \eta ))}^{ - 1}}} \right\rceil \Gamma _k^a{{(\gamma , t)}^{ - 1}}} \le \sum\limits_{t = {s_a}}^{{s_b}} {\left\lceil {{\rm{log}}(\Gamma _k^a(\gamma , t)){{({\rm{log}}(1 + \eta ))}^{ - 1}}} \right\rceil \Gamma _k^a{{(\gamma , t)}^{ - 1}}} }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \le {t_s}{\rm{log}}(\Gamma _k^a(\gamma , {t_b}))\Gamma _k^a{{(\gamma , {t_b})}^{ - 1}} \le {t_s}{\rm{log}}\left( {\frac{\gamma }{{1 - \gamma }}} \right)\frac{{1 - \gamma }}{\gamma }.} \end{array} $ | (B.10) |
最终,结合式(B.1)(B.4)(B.10)可得,若存在C, 使得χs≥logγ(1-γ)ζlog(Γka(γ, T))成立,则
| $ \begin{array}{*{20}{l}} {N_k^{n, s} \le \left\lceil {{t_s}(1 - \gamma )} \right\rceil \iota (\gamma , \sigma ){\gamma ^{ - 1/(1 - \gamma )}} + {\chi _s} + 2{t_s}{\rm{log}}\left( {\frac{\gamma }{{1 - \gamma }}} \right)\frac{{1 - \gamma }}{\gamma }}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\chi ^s} + {t_s}A(\gamma )(1 - \gamma ){\rm{log}}\left( {\frac{\gamma }{{1 - \gamma }}} \right).} \end{array} $ | (B.11) |
其中,A(γ)由下式给出:
TOD-N在时段ps的学习Regret可表示为
| $ R_s^{{\rm{TOD - N}}} = \sum\limits_{{H_k} \in {H_p}} {u_{\mathit{\boldsymbol{\phi}} (t)}^n} (t) - u_{{k^*}(t)}^n \le {\varDelta _{{\rm{max}}}}\sum\limits_{{H_k} \in {H_p}} E [N_k^{n, s}]. $ | (C.1) |
若
则存在C′,使得下式成立:
| $ R_s^{{\rm{TOD - N}}}/{t_s} \le {C^\prime }{\varDelta _{{\rm{max}}}}\sum\limits_{{H_k} \in {H_p}} {\sqrt {({s_b} - {s_a}){\chi _s}} } {\rm{log}}({s_b} - {s_a}). $ | (C.2) |
| [1] |
Chen S, Zhao J. The requirements, challenges, and technologies for 5G of terrestrial mobile telecommunication[J]. IEEE Communications Magazine, 2014, 52(5): 36-43. |
| [2] |
Bonomi F, Milito R, Zhu J, et al. Fog computing and its role in the internet of things[C]//Proceedings of the first edition of the MCC workshop on Mobile cloud computing. ACM, 2012: 13-16.
|
| [3] |
Mouradian C, Naboulsi D, Yangui S, et al. A comprehensive survey on fog computing:state-of-the-art and research challenges[J]. IEEE Communications Surveys & Tutorials, 2017, 20(1): 416-464. |
| [4] |
Yang Y. Multi-tier computing networks for intel-ligent IoT[J]. Nature Electronics, 2019, 2(1): 4. |
| [5] |
Chen N, Yang Y, Zhang T, et al. Fog as a service technology[J]. IEEE Communications Magazine, 2018, 56(11): 95-101. Doi:10.1109/MCOM.2017.1700465 |
| [6] |
Chen X, Jiao L, Li W, et al. Efficient multi-user computation offloading for mobile-edge cloud computing[J]. IEEE/ACM Transactions on Networking, 2016(5): 2795-2808. |
| [7] |
Dinh T Q, Tang J, La Q D, et al. Offloading in mobile edge computing:task allocation and computational frequency scaling[J]. IEEE Transactions on Communications, 2017, 65(8): 3571-3584. |
| [8] |
Liu Z, Yang X, Yang Y, et al. DATS:dispersive stable task scheduling in heterogeneous fog networks[J]. IEEE Internet of Things Journal, 2018, 6(2): 3423-3436. |
| [9] |
Mao Y, Zhang J, Song S H, et al. Stochastic joint radio and computational resource management for multi-user mobile-edge computing systems[J]. IEEE Transactions on Wireless Communications, 2017, 16(9): 5994-6009. Doi:10.1109/TWC.2017.2717986 |
| [10] |
Ouyang T, Zhou Z, Chen X. Follow me at the edge:mobility-aware dynamic service placement for mobile edge computing[J]. IEEE Journal on Selected Areas in Communications, 2018, 36(10): 2333-2345. Doi:10.1109/JSAC.2018.2869954 |
| [11] |
Tan Y, Wang K, Yang Y, et al. Delay-optimal task offloading for dynamic fog networks[C]//2019 IEEE International Conference on Communications (ICC). IEEE, 2019.doi: 10.1109/ICC.2019.8761113.
|
| [12] |
Gittins J, Glazebrook K, Weber R. Multi-armed bandit allocation indices[M]. Hoboken, US: John Wiley & Sons, 2011.
|
| [13] |
Auer P, Cesa-Bianchi N, Fischer P. Finite-time analysis of the multiarmed bandit problem[J]. Machine learning, 2002, 47(2/3): 235-256. Doi:10.1023/A:1013689704352 |
| [14] |
Bubeck S, Cesa-Bianchi N. Regret analysis of stochastic and nonstochastic multi-armed bandit problems[J]. Foundations and Trends® in Machine Learning, 2012, 5(1): 1-122. |
| [15] |
Garivier A, Moulines E. On upper-confidence bound policies for switching bandit problems[C]//International Conference on Algorithmic Learning Theory. Berlin, Heidelberg: Springer, 2011: 174-188.
|
| [16] |
田雷霞, 杨文国, 高随祥, 等. 不确定传输速率下无线资源调度问题的鲁棒优化模型[J]. 中国科学院大学学报, 2018, 35(1): 18-25. |
| [17] |
张剑, 邱玲, 陈正. 超密集网络中基于多连接的用户归属和功率控制联合优化[J]. 中国科学院大学学报, 2018, 35(1): 126-130. |
 2020, Vol. 37
2020, Vol. 37 


