近些年来，无人机的自主飞行问题备受研究者的关注。无人机想要完成这一任务，关键是运动规划(motion planning)^[1]。解决这一问题多数思路是预先规划生成合理的避障路径，再令无人机沿着路径行至目标点^[2]。典型的路径规划算法包括如A^*、D^*、Dijkstra的最短路径算法^[3]，基于快速随机搜索树(rapidly-exploring random tree，RRT)的一系列随机搜索算法，如DDRRT^[4]，RRT^*[5]以及人工势场法(artificial potential field)。人工势场法由Khatib于1986年提出^[6]，其基本思想是建立一种目标位置处的引力场和障碍物位置处的斥力场共同作用下的人工势场，在进行路径规划时沿着负梯度的方向进行路径搜索。然而传统人工势场法最大的缺陷在于势场中可能存在局部最小值点。为解决这一问题，文献[7]提出一种基于搜索的方法，但需要较高的计算量；文献[8]针对局部最小点设置附加的虚拟势场，文献[9]针对特定场景制定特殊的导航策略，但都不够简洁直观。

研究表明基于拉普拉斯方程的调和势场函数(harmonic potential field)不存在局部最小值^[10]。本文基于传感器探测生成的全局地图建立调和势场，工作步骤如下：

1) 采取边界元法(boundary element method，BEM)在欧式空间抽象出地图中的边界与障碍物，这种方法只需要利用地图中障碍物的边界单元，存储要求低并且可以快速求解出势场中任一点的梯度方向。

2) 设计线性二次高斯(linear quadratic Gaussian，LQG)控制器进行顶层的运动控制，在获得相应的参考速度方向后，控制器跟踪调整无人机姿态使自身速度方向趋向参考方向，最终逐渐飞向目标点。这种基于速度场的控制器，不需要机械地沿着预先规划好的路径行走，在应对传感器误差、环境影响上更具鲁棒性。

3) 在仿真平台Airsim进行试验。实验结果显示面对数量较多且分布复杂的障碍物，本文提出的算法可以有效引导无人机进行避障控制并最终到达目标点。

本文设计的算法脱胎于传统人工势场方法的思想，着力寻找解决传统方法固有缺陷的途径，在实际应用中更具备实用性与可靠性。拉普拉斯人工势场可建立在由传感器扫描重建的地图上(如点云)，不同于传统人工势场，这种方式对于障碍物的边界与位置描述更为精准，有利于保障无人机在复杂环境中的路径规划与飞行安全，也更适合拓展到实时探测与规划的层面。对比RRT、A^*、遗传算法等搜索算法，拉普拉斯人工势场从本质上避免了陷入“局部最优解”的烦恼，保证收敛到全局最优解。边界元法往往应用在力学等传统工程问题上，本文设计的算法将边界元法与地图模型特性良好结合，在求解导航问题时无须设置调试众多参数，在应用实现上更为简便可靠。

1 基于拉普拉斯方程的人工势场 1.1 人工势场的构建

人工势场法的基本思想是在无人机或者机器人的可行空间上建立合适的势函数，使其沿着函数负梯度方向运动，直至最终到达目标点。传统的人工势场法分别对障碍物跟目标点建立引力斥力函数从而进行代数叠加得到某一点合力函数。这种方法往往无法应对实际应用场景中各种复杂形态的障碍物，简单的几何替代会损失一定程度的规划精度；当地图中障碍物的数量增加、相对位置更为复杂后，这样产生的势场也容易变得局部畸形，比如可能存在的局部最小点将无人机困住无法逃离，某些点梯度方向的骤变导致最终的飞行路径不够光滑，加大了姿态控制的难度。

调和函数是建立人工势场的有利工具。考虑实空间 $\mathbb{R}$ⁿ内的开集Ω，其边界与闭包分别表示为∂Ω和$\bar \Omega $，非常值实函数ϕ定义在$\bar \Omega $上。如果实函数ϕ在非空开集Ω⊆$\mathbb{R}$ⁿ上二阶连续可微，且满足拉普拉斯方程，即

$ \Delta \phi : = \sum\limits_{i = 1}^n {\frac{{{\partial ^2}\phi }}{{\partial x_i^2}}} \equiv 0, $

那么称ϕ在Ω上是调和的，其中Δ为拉普拉斯算子。调和函数具有许多良好的性质，由强最大最小定律^[11]可知，ϕ在Ω上没有局部最小点，且可推导出如下的结论：

命题1   ϕ在闭集$\bar \Omega $上连续，在开集Ω上调和。若Ω有界且连通，且ϕ在边界∂Ω上的最大最小值分别为M和m，那么∀x∈Ω:m < ϕ(x) < M。

命题1表明在有界区域上的调和函数值被边界值所限定，且全局最大最小值只能出现在边界上。

由定义可知，调和函数是拉普拉斯方程的解，因而可以通过求解该偏微分方程构建调和势场。当合理设置边界条件时，相应的调和势场函数将唯一确定^[12]。常见的拉普拉斯方程边界条件有两种——Dirichlet与Neumann。前者是给势场边界设置固定的势场值，后者则是设置边界处的外法线方向导数。在二维空间下，上述初始边界条件下的拉普拉斯方程可表示为

$ {\frac{{{\partial ^2}\phi (x)}}{{\partial x_1^2}} + \frac{{{\partial ^2}\phi (x)}}{{\partial x_2^2}} = 0, \forall x \in \Omega , } $

(1)

$ {\phi (x) = \bar \phi (x), \forall x \in {\Gamma _1}, } $

(2)

$ {q(x) \equiv \frac{{\partial \phi (x)}}{{\partial n}} = \bar q(x), \forall x \in {\Gamma _2}.} $

(3)

式中：Γ₁∪Γ₂=∂Ω，${\bar \phi }$-与${\bar q}$分别是设置的边界势场值与外法线方向导数。

在可行空间上覆盖的调和函数没有局部极小点，二阶可微的性质令导出的梯度场仍是光滑的，非常适合后续的导航控制。将构建可行空间上的调和函数转化成式(1)~式(3)组成的边界值问题(boundary value problem)便是简单直观的方式。

设二维空间下地图的总构型为Ω⊆ $\mathbb{R}$²，目标所处的空间构型为 $\mathcal{G}$, 障碍物为 $\mathcal{O}$。对于无人机而言，其可到达区域 $\mathcal{F}$为总构型中除去目标与障碍物的部分, 即

$ \mathcal{F} = \{ q \in \Omega :q \notin \mathcal{G} \wedge q \notin \mathcal{O}\} . $

显然，$\mathcal{F}$是二维平面上定义的有界连通开集。称障碍物边界与总构型边界为阻碍边界Γ_o:

$ {\Gamma _o} = \partial \Omega \cup \partial \mathcal{O}, $

目标点的包围边界为目标边界Γ_g:

$ {\Gamma _{\rm{g}}} = \partial \mathcal{G}, $

二者共同构成可到达区域 $\mathcal{F}$的边界，即∂$\mathcal{F}$=Γ_g∪Γ_o。

基于上述定义可构建针对无人机运动规划的拉普拉斯方程，在阻碍边界与目标边界处分别设置Dirichlet条件，式(1)~式(3)转化为

$ {\frac{{{\partial ^2}\phi (x)}}{{\partial x_1^2}} + \frac{{{\partial ^2}\phi (x)}}{{\partial x_2^2}} = 0, \forall x \in \mathcal{F}, } $

(4)

$ {\phi (x) = M, \forall x \in {\Gamma _{\rm{o}}}, } $

(5)

$ {\phi (x) = m, \forall x \in {\Gamma _{\rm{g}}}.} $

(6)

式中：m与M均为实数，且M>m。

1.2 梯度场的求解

式(1)~式(3)共同构成的偏微分方程初始条件只与边界有关，可以转化为边界积分方程(boundary integration equation, BIE)，从而降低整个问题的维度。利用格林公式，可以得到相应边界积分方程^[13]，即$\forall x \in \bar \Omega $，

$ \begin{array}{l} \epsilon (x)\phi (x) = \int_S {[G(x, y)q(y) - } \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} H(x, y)\phi (y)]{\rm{d}}S(y), \end{array} $

(7)

其中：

$ \in (x) = \left\{ {\begin{array}{*{20}{l}} {1, }&{x \in \Omega }\\ {\frac{1}{2}, }&{x \in \partial \Omega } \end{array}} \right., $

(8)

$ {G(x, y) = \frac{1}{{2\pi }}{\rm{ln}}\left( {\frac{1}{r}} \right),} $

(9)

$ {H(x, y) = \frac{{\partial G(x, y)}}{{\partial \mathit{\boldsymbol{n}}}} = - \frac{1}{{2\pi r}}\frac{{\partial r}}{{\partial \mathit{\boldsymbol{n}}}}.} $

(10)

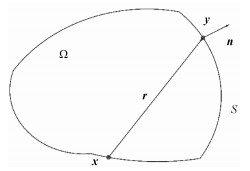
如图 1, S表示有界区域的边界曲线，y是其上一点，r表示x与y两点间的欧氏距离。G(x, y)为二维空间下的格林函数，n为外法线方向向量。区域内任一点的梯度也可直接导出，即∀x∈Ω, i=1, 2，

$ \begin{array}{l} \frac{{\partial \phi (x)}}{{\partial {x_i}}} = \int_S {\left[ {\frac{{\partial G(x, y)}}{{\partial {x_i}}}q(y) - \frac{{\partial H(x, y)}}{{\partial {x_i}}} \cdot } \right.} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \phi (y)]{\rm{d}}S(y). \end{array} $

(11)

结合式(7)~式(11)，一旦求解出边界上的势场值与外法线方向导数，就可以得到集合区域内任一点的势场值与梯度值。

由于边界积分方程没有解析解，采取边界元法进行离散数值求解。本文将边界S分割成N个常量单元，每个边界单元为直线段，表示为ΔS_i, i=1, …, N。每个单元中心上有一节点p_i, i=1, …, N，单元上的势场值ϕ_i与外法线方向导数q_i等于节点上的值，从而将边界积分方程转化为分段线积分

$ \frac{1}{2}{\phi _i} = \mathop \sum \limits_{j = 1}^N [{G_{ij}}{q_j} - {H_{ij}}{\phi _j}], \forall i = 1, \cdots , N, $

(12)

其中

$ {{G_{ij}} = \int_{\Delta Sj} G ({p_i}, y){\rm{d}}S(y), } $

(13)

$ {{H_{ij}} = \int_{\Delta Sj} H ({p_i}, y){\rm{d}}S(y).} $

(14)

本文采用文献[13]中提到的解析解求解式(13)、式(14)中的线积分。特别地，由于可达区域为多连通集，在总构型边界∂Ω上的元素其线积分为逆时针方向，反之障碍物边界与目标边界上的线积分方向为顺时针。令向量Φ=(ϕ₁, …, ϕ_N)，q=(q₁, …, q_N), 并构造矩阵H, G∈ $\mathbb{R}$^n×n使其第i行，第j列的元素分别为G_ij与H_ij，式(12)转化为

$ \frac{1}{2}\mathit{\boldsymbol{ \boldsymbol{\varPhi} }} + \mathit{\boldsymbol{H \boldsymbol{\varPhi} }} = \mathit{\boldsymbol{Gq}}. $

(15)

本文中拉普拉斯方程的初始条件均为Dirichlet条件，无须进行元素交换，式(15)即为形如Ax=b的标准线性方程组。一旦求解出方程的解，便可利用边界元素上所有的ϕ与q求解可达区域 $\mathcal{F}$中任意一点的负梯度值，并作为随后运动控制的参考速度方向。

2 基于梯度场的姿态控制

实际飞行过程中，无人机的建模不是单纯的质点，需要面对空气阻力、自身传感器误差等诸多问题。本节设计的顶层控制算法将连接路径规划与底层的姿态控制，当无人机到达某一位置时，上一节构建的人工势场能够实时导出其下一时刻的参考速度方向，控制算法将对应调整姿态使其逐渐趋向所设计的运动状态。

惯性坐标系采用NED坐标系，即x轴指向东，y轴指向北，z轴指向地面，令机身坐标系基底方向为[x′ y′ z′], 相关符号的详细含义参见表 1。

假设无人机保持恒定的飞行高度与飞行速率，且要求机头朝向与速度方向保持一致。受力分析可知，无人机的唯一动力来源为F_lift, 其方向垂直于机身平面(x′-y′平面)，因而其竖直分量等于重力，其水平分量为mu，可推导出z′=[－u_x－u_yg]^T。由于x′水平分量与速度方向一致，且与z′垂直，可得${\mathit{\boldsymbol{x}}^\prime } = {\left[ {{v_x}{v_y}\frac{{\left( {{v_x}{u_x} + {v_y}{u_y}} \right)}}{g}} \right]^{\rm{T}}}$，相应地y′=z′×x′，则描述无人机姿态的旋转矩阵R可由$\left[ {\frac{{{\mathit{\boldsymbol{x}}^\prime }}}{{\parallel \mathit{\boldsymbol{x}}\parallel }}\frac{{{\mathit{\boldsymbol{y}}^\prime }}}{{\parallel \mathit{\boldsymbol{y}}\parallel }}\frac{{{\mathit{\boldsymbol{z}}^\prime }}}{{\parallel \mathit{\boldsymbol{z}}\parallel }}} \right]$确定。

旋转矩阵R描述输入分量u到无人机姿态的映射，同时将姿态控制分解为对u的控制。考虑无人机飞行时的运动学方程，它被描述成如下的线性系统：

$ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{\dot v}} = \mathit{\boldsymbol{Av}} + \mathit{\boldsymbol{u}} + \mathit{\boldsymbol{w}}, }\\ {\mathit{\boldsymbol{\rho }} = \mathit{\boldsymbol{v}} + \mathit{\boldsymbol{\tilde w}}.} \end{array} $

(16)

其中ρ=[ρ_x ρ_y]^T, $\mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} { - \frac{k}{m}}&0\\ 0&{ - \frac{k}{m}} \end{array}} \right]$，w与${\mathit{\boldsymbol{\tilde w}}}$分别为衡量系统与观测扰动的高斯白噪声，W与${\mathit{\boldsymbol{\tilde W}}}$为二阶半正定矩阵，满足

$ E(\mathit{\boldsymbol{w}}{\mathit{\boldsymbol{w}}^{\rm{T}}}) = W, E(\mathit{\boldsymbol{\tilde w}}{\mathit{\boldsymbol{\tilde w}}^{\rm{T}}}) = \tilde W, E(\mathit{\boldsymbol{w}}{\mathit{\boldsymbol{\tilde w}}^{\rm{T}}}) = 0. $

由人工势场负梯度方向导出恒定速率下的参考速度，用r(t)表示；$\mathit{\boldsymbol{e}}(t) = \int_0^t {(\mathit{\boldsymbol{r}}(} \tau ) - \mathit{\boldsymbol{\rho }}(\tau )){\rm{d}}\mathit{\boldsymbol{\tau }}$表示控制误差，整个系统的控制目标即为

$ \begin{array}{l} {\rm{min}}\mathbb{E}\left\{ {\mathop {{\rm{lim}}}\limits_{\tau \to \infty } \frac{1}{\tau }\mathop \smallint \nolimits_0^\tau \left[ {{\mathit{\boldsymbol{v}}^{\rm{T}}}\quad {\mathit{\boldsymbol{e}}^{\rm{T}}}\quad {\mathit{\boldsymbol{u}}^{\rm{T}}}} \right]} \right.\\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{Q}}&{}&{}\\ {}&{{\mathit{\boldsymbol{Q}}_e}}&{}\\ {}&{}&\mathit{\boldsymbol{R}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{v}}\\ \mathit{\boldsymbol{e}}\\ \mathit{\boldsymbol{u}} \end{array}} \right]{\rm{d}}t} \right\}. \end{array} $

(17)

其中Q为二阶半正定矩阵，Q_e与R为二阶正定矩阵。

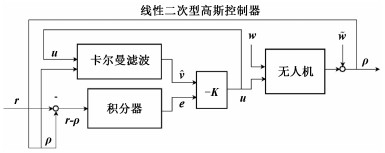
本文采用线性二次高斯(LQG)控制器^[14-15]解决上述最优控制问题。LQG控制器将线性二次调节器(linear quadratic regulator，LQR)与卡尔曼滤波相结合，具有较好的控制精度与鲁棒性。图 2展示了控制系统的整体架构。根据分离原理，状态观测器与状态反馈系统可分别独立设计。首先，利用卡尔曼滤波器对观测值进行优化估计，即最小化期望估计误差$\mathop {\lim }\limits_{t \to \infty } E({(\mathit{\boldsymbol{v}} - \mathit{\boldsymbol{\widehat v}})^{\rm{T}}}(\mathit{\boldsymbol{v}} - \mathit{\boldsymbol{\widehat v}}))$。估计值的状态方程表示如下

$ \mathit{\boldsymbol{\dot {\hat \nu }}} = \mathit{\boldsymbol{A\hat v}} + \mathit{\boldsymbol{u}} + {\mathit{\boldsymbol{K}}_f}(\mathit{\boldsymbol{\rho }} - \mathit{\boldsymbol{\hat v}}), $

其中K_f为卡尔曼系数。求解对应的Riccati方程

$ \mathit{\boldsymbol{AP}} + \mathit{\boldsymbol{P}}{\mathit{\boldsymbol{A}}^{\rm{T}}} - \mathit{\boldsymbol{P}}{\mathit{\boldsymbol{\tilde W}}^{ - 1}}\mathit{\boldsymbol{P}} + \mathit{\boldsymbol{W}} = 0, $

可得到${\mathit{\boldsymbol{K}}_f} = \mathit{\boldsymbol{P}}{\mathit{\boldsymbol{\widetilde W}}^{ - 1}}$。对于无人机模型而言，控制率u以状态反馈的形式给出：

$ \mathit{\boldsymbol{u}} = - \mathit{\boldsymbol{K}}\left[ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\hat v}}}\\ \mathit{\boldsymbol{e}} \end{array}} \right], $

K∈ $\mathbb{R}$^2×4为对应增广状态方程下LQR调节器的反馈系数。在忽略系统扰动与观测噪声的情况下，增广系统表示为

$ \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{\dot v}}}\\ {\mathit{\boldsymbol{\dot e}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{A}}&0\\ { - \mathit{\boldsymbol{I}}}&0 \end{array}} \right]\left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{v}}\\ \mathit{\boldsymbol{e}} \end{array}} \right] + \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{I}}\\ 0 \end{array}} \right]\mathit{\boldsymbol{u}} + \left[ {\begin{array}{*{20}{l}} 0\\ \mathit{\boldsymbol{I}} \end{array}} \right]\mathit{\boldsymbol{r}}. $

相应的目标函数为

$ {\rm{min}}\int_0^\infty {\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{v}}^{\rm{T}}}}&{{\mathit{\boldsymbol{e}}^{\rm{T}}}}&{{\mathit{\boldsymbol{u}}^{\rm{T}}}} \end{array}} \right]} \left[ {\begin{array}{*{20}{c}} \mathit{\boldsymbol{Q}}&{}&{}\\ {}&{{\mathit{\boldsymbol{Q}}_e}}&{}\\ {}&{}&\mathit{\boldsymbol{R}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{v}}\\ \mathit{\boldsymbol{e}}\\ \mathit{\boldsymbol{u}} \end{array}} \right]{\rm{d}}t. $

类似地，令增广系统中的A系数矩阵为$\mathit{\boldsymbol{\tilde A}} \in {\mathbb{R}^{4 \times 4}}$，B系数矩阵为$\mathit{\boldsymbol{\tilde B}} \in {\mathbb{R}^{4 \times 2}}$, 求解对应的Riccati方程

$ {\mathit{\boldsymbol{\tilde A}}^{\rm{T}}}\mathit{\boldsymbol{X}} + \mathit{\boldsymbol{X\tilde A}} - X\mathit{\boldsymbol{\tilde B}}{\mathit{\boldsymbol{R}}^{ - 1}}{\mathit{\boldsymbol{\tilde B}}^{\rm{T}}}\mathit{\boldsymbol{X}} + \left[ {\begin{array}{*{20}{l}} \mathit{\boldsymbol{Q}}&{}\\ {}&{{\mathit{\boldsymbol{Q}}_e}} \end{array}} \right] = 0, $

则反馈系数$\mathit{\boldsymbol{K}} = {\mathit{\boldsymbol{R}}^{ - 1}}\mathit{\boldsymbol{\tilde BX}}$。

3 实验仿真与分析

本文采用Airsim^[16]作为实验仿真平台。Airsim是微软开发的一款开源自动驾驶仿真平台，基于虚幻引擎打造，能最大限度地模拟现实环境中的物理表现。Airsim为无人机模型提供基于PX4的底层控制，将上节提到的旋转矩阵R转换为四元数即可直接控制无人机的运动。

本文的Airsim仿真程序基于C++编写，CPU为Xeon E5-2650，主频2.3 GHz。为检验算法的有效性跟可靠性，建立多种不同类型的全局地图。地图同样采用NED坐标系，无人机的高度限定在5 m。实验1中，底边长为20 m的立方柱紧密排列，构成一个类似走廊的地图环境。地图的总区域为一个140 m×110 m的截面，目标点位于(40 m, 60 m)，以边长为1的正方形包围构成目标边界。设阻碍边界Γ_o初值为100，目标边界Γ_g初值为0，使用BEM算法求解对应的拉普拉斯方程，可求得如图 3的人工势场。图 3(a)、3(b)分别展示人工势场的等高线势场与流线图。

图 3(a)中障碍物被黑色覆盖，可到达区域 $\mathcal{F}$的边界由实线段组成。可到达区域中只存在目标点处的唯一极小点，势场值在离目标点较远处变化不大，在目标点附近快速下降。由于姿态控制只需要势场的梯度方向，势场的绝对值对于后续控制没有影响。事实上，一旦可行区域的边界形态确定，相应的梯度场方向就可确定，不会受到边界初值大小的影响。图 3(b)中的流线图刻画了理想状态下，以梯度方向为速度方向的无人机的飞行路径。可以看到处于可行区域内的任意一点在人工势场的引导下最终都会趋向目标点。

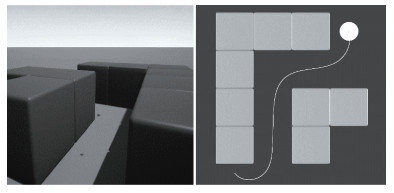
图 4展示Airsim中的实际仿真结果。无人机的质量设定为1 kg，起点位于(-20 m, -15 m)，LQG控制器中的相应参数Q=I，Q_e=100 I, R=I, W=0.01I, $\mathit{\boldsymbol{\tilde W = }}0.1\mathit{\boldsymbol{I}}$，飞行速度大小‖v‖维持在3 m/s。当程序获取到地图全局信息后，通过BEM求解建立人工势场。求解过程一旦完成，无人机可实时计算出下一时刻的参考速度方向，并在控制器的引导下调整姿态从而逐步达到目标点。仿真得到的无人机实际轨迹与图 3中的流线图几乎一致。可以看到，运动轨迹的光滑性体现了拉普拉斯势场无限可微的优势，这一特点也更好地适应对无人机的动力控制；另一方面路径选择也达到了路径长度最优与碰撞概率最小的某种平衡。

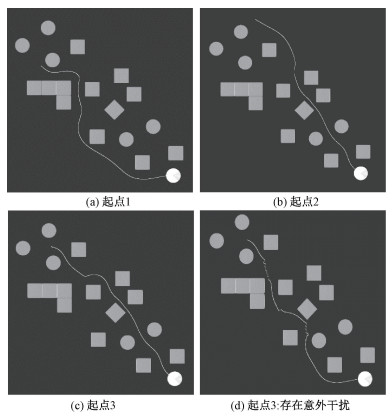
实验2中，地图中障碍物的数量增多，且分布更为凌乱。图 5(a)~5(c)分别展示不同起点下无人机的飞行轨迹。结果显示，无论起点在何处，无人机都可以自行选择合适的飞行方向达到目标点，且不需要再进行重复的规划计算。传统的路径规划与导航控制算法大都采取预先根据地图规划并生成路径，再利用控制器控制无人机进行路径跟踪的理念。在实际应用中，一旦遭遇强风、信号干扰等意外，无人机的底层控制器超出稳态，其位置发生偏移，路径跟踪器将逐渐引导无人机回到之前的路径或进行重新规划。本文提出的算法在应对这种情况时有明显的优势，图 5(d)展示强烈外界干扰后，无人机自行调整的飞行结果。在Airsim中模拟无人机遭遇瞬间大风后发生短暂失控的情形，其中折线段表示无人机的位置瞬间偏离，图 5(d)中的无人机起点与图 5(c)中一致，但由于遭遇意外干扰，在岔路口处路径选择与图 5(c)并不一致，从而使得整个飞机轨迹都截然不同。这种调整并不需要额外的程序设计与线程来应对，节约了计算资源，实时性高，非常适合实际场景的应用。

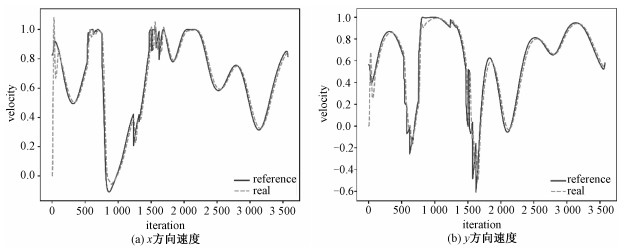
仿真实验结果表明本文设计的算法非常适合迁移到实际飞行的应用中。实验2中的全局地图抽象得到的476个边界元，采用单线程求解时间仅需2.01 s。这一步骤可由无人机自带的处理器进行计算，也可线下计算通信传输，通信负担仅为每个边界元的位置坐标与H, G两个n×n矩阵。模拟飞行中，将无人机的底层控制频率设为100 Hz，在每个控制周期内，无人机根据自身位置实时计算出当前的参考速度，平均耗时仅在3 ms左右。图 6展示整个飞行过程中无人机的飞行速度变化，其中实线为参考速度值，虚线为实际值。即便当参考速度发生突变时，控制器也能及时响应，迅速改变调整无人机的速度达到理想状态。

4 结论

本文提出基于拉普拉斯方程的人工势场，

1) 根据全局地图抽象出可行区域边界，合理设置初始边界条件，采用边界元法求解相应方程。求解得出的调和势场相较传统人工势场可以适应各种形态复杂的障碍物，内部不存在局部极小点，二阶可微使得导出的梯度场连续光滑，有利于无人机等移动机器人的控制；

2) 基于人工势场导出的速度场，设计关于无人机姿态的控制器。控制器使无人机合理调整姿态，不断追踪更新中的参考速度，直至最终达到目标点；

3) 基于Airsim的拟真环境的仿真实验，验证了算法的有效性与鲁棒性。在应对外界环境的意外干扰下，算法保证了无人机路径与运动状态的合理选择，具有较好的实时性与较广泛的实际应用前景。鉴于本文提出的人工势场依旧构建在二维空间，对于三维空间下的应用扩展将是后续研究的方向。