2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
无线传感器网络(wireless sensor network,WSN)是由大量小尺寸、低成本的微传感器节点通过自组织和多跳方式形成的通信网络[1],将传感器数据发送给汇聚节点以实现对特定区域的环境信息的探测和感知。WSN中传感器节点能量有限,并且节点电池由于环境因素难以替换[2]。WSN中传感器节点在监测区域分布较密,会导致监测区域的重叠,产生的大量冗余数据传输至汇聚节点会造成额外的能量消耗,缩短整个网络的生命周期[3]。对WSN数据进行数据融合处理,能有效地减少冗余数据,降低传感器节点能耗,延长网络生命周期[4]。
针对无线传感网数据传输能耗较高的问题,科研人员提出各种WSN数据融合算法来减少数据传输,以降低传感器节点能耗[5]。文献[3]设计一种基于反向传播(back propagation,BP)神经网络的数据融合算法(back-propagation networks data aggregation,BPNDA), 该算法将BP神经网络和传感器网络分簇路由协议有机结合, 将每个簇设计成一个神经网络模型, 通过神经网络提取对原始数据进行特征提取, 然后将特征数据发送给汇聚节点, 从而提高数据收集效率, 延长网络生存时间。但是BP神经网络对于初始权值和阈值很敏感,易陷入局部极小值。文献[6]利用遗传算法对BP神经网络的权值和阈值参数进行优化,提出一种基于遗传算法(genetic algorithm,GA)的BP神经网络数据融合算法GABP算法,能有效减少冗余数据,延长网络生命周期。但遗传算法存在搜索能力较差,求解速度较慢的缺陷。文献[7]把蚁群算法应用到BP神经网络,对其结构及参数进行优化,以克服BP神经网络容易陷入局部最优解的缺点。利用优化后的BP神经网络进行数据融合,可以有效提取特征数据,延长网络生命周期。文献[8]提出一种基于粒子群(particle swarm optimization,PSO)优化BP神经网络的无线传感器网络数据融合算法PSO-BP,利用粒子群算法优化BP神经网络参数,将优化后的BP神经网络和传感器网络分簇路由协议有机结合,有效提升数据融合效率,延长网络生命周期。但是由于粒子群算法种群搜索空间中多样性的丢失,所以粒子群算法存在陷入局部最优解的缺点[9]。
综上所述,传统BP神经网络应用于无线传感器网络中存在训练困难、易陷入局部最优解的缺陷;GABP算法寻优效果受种群初始分布影响较大,求解速度缓慢;PSO-BP算法中粒子群算法存在早熟收敛、维数灾难、缺乏多样性、易于陷入局部极值等问题,仍具有较大优化空间。本文以优化寻优性能和融合精度为目标,提出一种基于天牛须搜索(beetle antennae search,BAS)算子改进粒子群算法的WSN数据融合算法BSO-BP算法, 通过天牛须搜索算子优化粒子群算法[10],增加粒子群算法的搜索空间多样性,丰富粒子群算法的寻优空间以避免陷入局部最优解。利用优化后的粒子群算法对BP神经网络的初始权值和阈值参数进行优化,得到的全局较优解作为BP神经网络结构参数的初始值并进行进一步优化训练,从而克服BP神经网络训练极易陷入局部最优解的缺陷,避免传统BP神经网络初始权值和阈值参数随机选取导致的网络震荡,提高BP神经网络的泛化能力和收敛能力。将BSOBP算法运用到无线传感器网络分簇路由数据融合中,簇首节点利用优化后的BP神经网络对传感器采集数据进行数据融合提取特征数据,数据精度具有较高提升,将融合后的数据发送至基站节点,有效减少冗余数据传输,延长网络生命周期。
1 改进PSO算法 1.1 粒子群算法粒子群(PSO)算法是一种基于鸟类群体的社会行为的群体优化算法,通过群体信息共享机制寻找当前最优值以获取全局最优值。每个粒子的行为模仿鸟类飞行,粒子位置根据自身的惯性速度、历史经验以及群体社会经验来进行寻优更新[11],寻优公式如下
| $ \begin{array}{l} \mathit{\boldsymbol{v}}_{id}^{k + 1} = w\mathit{\boldsymbol{v}}_{id}^k + {c_1}{r_1}(\mathit{\boldsymbol{p}}best_{id}^k - x_{id}^k) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {c_2}{r_2}(\mathit{\boldsymbol{g}}best_{id}^k - x_{id}^k), \end{array} $ | (1) |
| $ \mathit{\boldsymbol{x}}_{id}^{k + 1} = \mathit{\boldsymbol{x}}_{id}^k + \mathit{\boldsymbol{v}}_{id}^{k + 1}. $ | (2) |
式中:d=1, 2, …, D(D表示粒子总维度),i=1, 2, …, N(N为粒子群粒子数量),k为当前迭代次数,vidk表示第k次迭代时粒子i的第d维位置矢量,xidk表示第k次迭代时粒子i的第d维位置矢量,w为惯性权重,c1和c2为加速度常数,r1和r2为两个取值范围为[0, 1]的随机函数。pbestidk表示粒子i的历史最优适应度在第k次迭代中的第d维位置,gbestidk表示群体粒子的历史最优适应度在第k次迭代中的第d维位置矢量。
1.2 基于天牛须搜索算法对粒子群的改进天牛须搜索(BAS)算法是由Jiang和Li在2018年提出的一种新型启发式算法[12],它是一项基于天牛觅食原理的适用于目标函数优化的新技术,其灵感来源于天牛觅食过程:天牛觅食时,通过食物气味强弱来觅食。天牛有两只灵敏的长触角,如果左触角收到的气味强度大于右边,那下一步天牛就会往左边飞,反之则往右边飞。依据这一简单原理天牛就可以有效找到食物,BAS对函数具体形式没有要求,不需要梯度信息,就可以实现高效寻优。BAS收敛快,并且算法简单容易实现,容易移植到单片机运行,很适合实时性要求较高的场景。天牛须搜索算法模型主要包括搜索行为和检测行为:
1) 创建天牛须朝向的归一化随机向量
| $ \mathit{\boldsymbol{b}} = \frac{{ {\rm{rands}} (m, 1)}}{{\left\| {{\rm{rands}} (m, 1)} \right\|}}, $ | (3) |
式中:rands()为随机函数;m表示空间维度。
2) 创建天牛左右须空间搜索模型,模拟天牛须行为
| $ \left\{ {\begin{array}{*{20}{l}} {{x_{{\rm{r}}k}} = {x^k} + {d^k} \times \mathit{\boldsymbol{b}}/2}\\ {{x_{{\rm{l}}k}} = {x^k} - {d^k} \times \mathit{\boldsymbol{b}}/2} \end{array}} \right.. $ | (4) |
式中:xrk表示天牛右须在第k次迭代时的位置坐标;xlk表示天牛左须在第k次迭代时的位置坐标;xk表示天牛在第k次迭代时的质心坐标;dk表示左右两须之间的搜索距离。
3) 根据适应度函数判断左右须气味强度差异,即计算f(xlk)和f(xrk)的强度,f为适应度函数。
4) 迭代更新天牛的位置
| $ {x^{k + 1}} = {x^k} - {\delta ^k} \times \mathit{\boldsymbol{b}} \times {\rm{sign}} (f({x_{{\rm{r}}k}}) - f({x_{{\rm{l}}k}})), $ | (5) |
式中:δk表示在第k次迭代时的步长因子;sign()为符号函数。
5) 搜索距离和步长更新
| $ \begin{array}{*{20}{l}} {{d^k} = {\eta _d}{d^{k - 1}} + {d_0}, }\\ {{\delta ^k} = {\eta _\delta }{\delta ^{k - 1}} + {\delta _0}.} \end{array} $ | (6) |
式中:ηd代表搜索距离的衰减更新系数;ηδ代表步长的衰减更新系数;d0和δ0分别是最小距离阈值和最小步长阈值,避免dk和δk为0。
天牛须搜索算法的搜索行为对于PSO算法有很大作用,赋予PSO算法中粒子天牛搜索行为特性,可以有效增加粒子种群变化的多样性,克服PSO算法寻优过程中易陷入局部最优的问题。本文根据基于适应度值的轮盘赌算法选取多个粒子进行天牛须搜索,每次迭代选取赋予天牛搜索行为的粒子个数为
| $ {N_i} = {\rm{ swarmize }} - \left( {\frac{{{\rm{ iter }}}}{{{\rm{maxgen }}}}} \right)({\rm{ swarmize }} - 2), $ | (7) |
式中:swarmize为粒子种群粒子总数,iter和maxgen分别为当前迭代次数和总迭代次数。粒子群搜索初期,具有天牛搜索行为的粒子能使种群更具多样性,扩展了寻找最优解的范围,避免陷入局部最优解,随着迭代次数增加,粒子群越来越收敛,此时应减少具有天牛搜索行为的粒子数量,有利于减少计算量,快速收敛。具有天牛搜索行为的粒子根据式(3)随机生成天牛须朝向向量, 并对式(4)进行修改确定天牛须左右须坐标
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{x}}_{i{\rm{r}}d}^k = \mathit{\boldsymbol{x}}_{id}^k + \mathit{\boldsymbol{v}}_{id}^k \times {d^k}/2}\\ {\mathit{\boldsymbol{x}}_{i{\rm{l}}d}^k = \mathit{\boldsymbol{x}}_{id}^k - \mathit{\boldsymbol{v}}_{id}^k \times {d^k}/2} \end{array}} \right., $ | (8) |
式中:xirdk和xildk分别表示第k次迭代时具有天牛搜索行为的粒子i的左右须第d维位置矢量。
引入粒子天牛须搜索行为增量
| $ \xi _{id}^{k + 1} = {\delta ^k} \times v_{id}^k \times {\rm{sign}} (f(x_{i{\rm{r}}d}^k) - f(x_{i{\rm{l}}d}^k)), $ | (9) |
式中:ξidk+1代表第k+1次迭代时的搜索行为增量。对粒子群的寻优计算式进行改进,添加天牛须搜索行为增量
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{v}}_{id}^{k + 1} = w\mathit{\boldsymbol{v}}_{id}^k + {c_1}{r_1}(\mathit{\boldsymbol{p}}best_{id}^k - x_{id}^k) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {c_2}{r_2}(\mathit{\boldsymbol{g}}best_{id}^k - x_{id}^k), } \end{array} $ | (10) |
| $ \mathit{\boldsymbol{x}}_{id}^{k + 1} = \mathit{\boldsymbol{x}}_{id}^k + (1 - \lambda )\mathit{\boldsymbol{v}}_{id}^{k + 1} + \lambda \xi _{id}^{k + 1}. $ | (11) |
式中:w为惯性权重,反映粒子的运动习惯,理论上,w取值较小时局部搜索能力较强,w取值较大可以增强全局搜索能力。文献[13]分析比较多种动态调整惯性权重的方法,发现对于多峰函数优化,凸函数递减法综合来说收敛速度最快,求解精度较高。因此本文惯性权重w采用凸函数递减法
| $ w = ({w_{{\rm{max}}}} - {w_{{\rm{min}}}}){\left( {1 - \frac{{{\rm{ iter }}}}{{{\rm{maxgen }}}}} \right)^3} + {w_{{\rm{min}}}}. $ | (12) |
式中:wmax和wmin分别为惯性权重上下限值,iter和maxgen分别为当前迭代次数和总迭代次数。c1和c2为学习因子,c1表示粒子对自身历史经验的学习,c2表示粒子对共享的群体历史经验的学习[14],PSO算法运行初期,侧重于粒子个体的探索认知,末期需要增强对群体经验的学习能力,因此,c1和c2分别随着迭代次数递减和递增:
| $ {{c_1} = {c_m} + \frac{{{\rm{ iter }}}}{{{\rm{maxgen }}}}({c_n} - {c_m}), } $ | (13) |
| $ {{c_2} = {c_n} + \frac{{{\rm{ iter }}}}{{{\rm{maxgen }}}}({c_m} - {c_n}).} $ | (14) |
式中:cm和cn为常数,满足cm>cn。
改进PSO算法中,λ为天牛搜索行为增量的权重因子,搜索前期,天牛搜索行为增量权重较大有利于增加全局搜索能力,后期随着具有天牛搜索行为的粒子数量的减少,天牛搜索行为增量权重也应当降低,因此搜索行为增量权重因子λ的赋值如下
| $ \lambda = ({\lambda _{{\rm{max}}}} - {\lambda _{{\rm{min}}}})\left( {1 - \frac{{{\rm{ iter }}}}{{{\rm{ maxgen }}}}} \right) + {\lambda _{{\rm{min}}}}. $ | (15) |
式中:λmax和λmin为常数,分别代表增量权重因子的上下限值。
2 BSO-BP数据融合算法 2.1 算法网络模型WSN多传感器数据融合算法可分为数据级融合、特征性融合和决策级融合3类。决策级融合通过不同种类的传感器观测同一个目标,例如温度、湿度、风速等传感器感知森林某区域环境信息,每个传感器在本地完成包括预处理、特征抽取、识别或判决等基本处理,以建立对所观察目标的初步结论。然后通过关联处理进行决策层融合判决,最终获得联合推断结果。决策级融合包括贝叶斯估计法、专家系统、神经网络法、模糊集理论等,本文对决策级融合中的神经网络算法进行研究改进。
神经网络是由大量具有运算能力的单元广泛互联而组成的,通过高效的学习机制模拟人脑信息处理的过程。神经网络由于其强大的计算能力,因此在信号处理、计算机视觉、自然语言优化处理等领域应用广泛[15]。BP神经网络是一种典型的多层前向型神经网络[16]。BP神经网络由输入层、隐藏层、输出层组成,它利用学习机制来存储输入和输出的映射关系,其权值和阈值参数通常采用反向传播的策略,借助最速梯度信息来获得使网络误差最小化的参数组合,有很强的非线性映射能力、自学习和自适应能力、泛化能力和容错能力。将BP神经网络模型利用到WSN中处理数据融合问题,能有效降低数据特征维数,提高数据融合效率和精度,从而减少节点能耗。利用BP神经网络结合无线传感器分簇路由算法构建WSN数据融合模型,网络结构如图 1所示。

|
Download:
|
| 图 1 BSO-BP算法神经网络结构 Fig. 1 Neural network architecture of BSO-BP algorithm | |
按照LEACH(low energy adaptive clustering hierarchy)分簇路由算法完成分簇后,簇内传感器节点首先对监测到的原始数据进行滤波等预处理,然后将数据传输至簇首节点,簇首节点利用BP神经网络对数据进行融合,提取特征数据,减少冗余数据,将融合后的特征数据传输至汇聚节点,从而减少数据传输量,延长网络生命周期[17]。但传统BP神经网络也存在一定缺陷,初始权值参数的选择具有随机性,网络对初始连接权值的选择很敏感,初值选取不当会导致训练结果不佳,易陷入局部最优解。
2.2 算法步骤利用改进后的粒子群算法对BP神经网络数据融合算法进行优化,并应用于LEACH分簇路由算法中,提出一种新型智能数据融合算法——BSO-BP算法。
LEACH分簇路由算法中需要定期更新簇首以平衡能耗,相应地簇集也需动态更新,簇首的变化会导致簇内BP神经网络结构的变化,BP神经网络进行数据融合需要权值和阈值参数,因此簇首更新后,在WSN进入自治工作状态前,BP神经网络的参数也需更新。WSN中传感器节点运算能力、节点能量以及存储能力有限,因此参数的训练更新在基站节点进行,BSO-BP算法整体步骤如下:
步骤1:每轮簇首节点更新,分簇形成后,簇首记录簇内节点信息并传输至基站节点。
步骤2:基站根据簇集信息确定BP神经网络结构。
步骤3:基站选取与该分簇相匹配的样本数据集,结合改进后的PSO算法对BP神经网络进行训练优化,以得到对应簇集的BP神经网络连接权值和阈值参数。
步骤4:基站将相应簇集的BP神经网络连接权值和阈值参数发送至各簇集节点内,存储参数供下次使用。
步骤5:每个簇集根据接收到的参数报文构建对应的BP神经网络,簇首节点对簇内成员节点上传的数据进行融合处理并将结果传输至基站节点。至此,完成一轮分簇路由通信过程。
上述步骤3中改进PSO算法优化BP神经网络算法的目的是优化BP神经网络的权值阈值参数。利用改进PSO对BP神经网络的连接权值和阈值参数进行优化,获得一个全局优化解。将全局优化解作为BP神经网络的初始权值和阈值参数,BP神经网络进一步训练优化,以获得全局最优参数。这样,克服了BP神经网络由于初始权值选取的随机性导致的收敛性不佳、训练时间较长、易陷入局部最优解等缺陷,提高了BP神经网络的收敛能力和求解精度,改进PSO算法优化BP神经网络算法具体实现步骤如下:
Step 1:确定搜索空间维度。WSN分簇形成后,每个簇内成员节点个数即是输入层神经元个数M,隐藏层神经元个数为N,输出层神经元个数为1。因此,搜索空间维度D=M×N+N×1+N+1。
Step 2:初始化设置。初始化n个粒子的初始位置向量xi(i=1, 2, …, n), 其中xi=(xi1, xi2, …, xiD)为第i个粒子的D维搜索向量,包含BP神经网络中输入层和隐藏层的权值,隐藏层和输出层的权值,以及隐藏层和输出层的阈值;初始化n个粒子的速度向量vi(i=1, 2, …, n), 其中vi=(vi1, vi2, …, viD)为第i个粒子的速度向量;初始化速度变化范围[-Vmax, Vmax];初始化最大迭代次数K。
Step 3:定义适应度函数。对样本数据进行融合,根据样本数据的均方根误差(RMSE)作为适应度函数
| $ f({x_i}) = \sqrt {\frac{1}{m}\sum\limits_{i = 1}^m {{{( {\rm{trai}}{{\rm{n}}_i} - {y_i})}^2}} } , $ | (16) |
式中:m为样本数据训练条目数量,traini是第i个样本数据的融合预测结果,yi为第i个样本数据的实测值。
Step 4:计算每个粒子的适应度函数值。每个粒子个体需要记忆自身搜寻的最佳位置,第i个粒子自身搜寻过的最佳位置记作pbestid=(pi1, pi2, …, piD),同时群体搜寻到的最佳位置也会被记录,记作gbestd=(g1, g2, …., gD)。
Step 5:根据公式(8)更新天牛左右须搜索空间位置, 并分别计算f(xl)和f(xr)。
Step 6:根据公式(9)计算搜索行为增量。
Step 7:根据公式(10)公式(11)更新粒子速度和位置。
Step 8:迭代控制。判断是否到达迭代次数或者当前位置的适应度函数值是否达到理想值,如果满足迭代停止条件,则进行下一步骤,否则继续从Step 4迭代搜索,并根据式(12)~式(15)分别更新惯性权重w、学习因子c1和c2以及天牛搜索行为增量的权重因子λ。
Step 9:训练BP神经网络。种群最佳位置gbestd即是BP神经网络最佳初始权值和阈值,BP神经网络利用gbestd作为初始参数进行训练学习直至权值和阈值参数确定。
3 仿真结果与分析利用MATLAB 2016a进行仿真实验,与GABP算法和PSOBP算法进行对比实验,从数据融合精度、网络生命周期以及迭代收敛性能3个方面进行分析。无线传感网络仿真参数如表 1所示。
|
|
表 1 仿真参数表 Table 1 Simulation parameters |
为验证算法数据融合性能,本文采用森林火灾面积数据集为研究样本,该数据集提供了多项气象数据包括温度、湿度、风速、降雨量等以及对应的森林火灾面积数据。无线传感器网络通过采集气象数据能有效监测小型火灾,对保障森林安全有重要意义。本文仿真实验中,BP神经网络模型为4输入、1输出的单隐藏层结构。选取数据集中传感器监测到的4项气象数据(温度、湿度、风速、降雨量)作为BP输入层参数,森林火灾面积数据作为输出层参数。隐藏层神经元的数量关系到网络的学习信息处理能力和结构复杂性,需要选择合适的隐藏层神经元数目。根据隐藏层神经元数量经验公式
| $ k = \sqrt {m + n} + a, a = 1, 2, 3, \cdots , 10, $ | (17) |
隐藏层神经元数量取值范围为[4, 12],表 2为不同神经元数量下的融合误差RMSE值对比结果,其中RMSE量纲为森林火灾面积,单位为hm2。
|
|
表 2 隐藏层神经元数量与RMSE值 Table 2 Neurons'number of hidden layers vs. RMSE |
比较不同隐藏层神经元数量下的融合误差RMSE值,隐藏层神经元数量设置为7时,融合误差RMSE值最小,因此,本文中BP神经网络为4-7-1的单隐层结构,待优化参数个数为4×7+7+7×1+1=43。
1) 融合精度
融合精度对比采用平均相对误差(average relative error,AvRE)、均方根误差(root mean squared error,RMSE)以及拟合优度(goodness of fit,R2)作为评价指标,计算公式如下:
| $ {\rm{AvRE}} = \frac{{\sum\limits_{i = 1}^n {\frac{{|{u_i} - {y_i}|}}{{{y_i}}}} }}{N}, i = 1, 2, \cdots , n, $ | (18) |
| $ {\rm{ RMSE }} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^n {{{({u_i} - {y_i})}^2}} } , i = 1, 2, \cdots , n, $ | (19) |
| $ {R^2} = \frac{{\sum\limits_{i = 1}^n {{{({u_i} - \bar y)}^2}} }}{{\sum\limits_{i = 1}^n {{{({y_i} - \bar y)}^2}} }}, i = 1, 2, \cdots , n. $ | (20) |
式中:ui为第i个样本数据的融合值,yi为第i个样本数据的实际值,
|
Download:
|
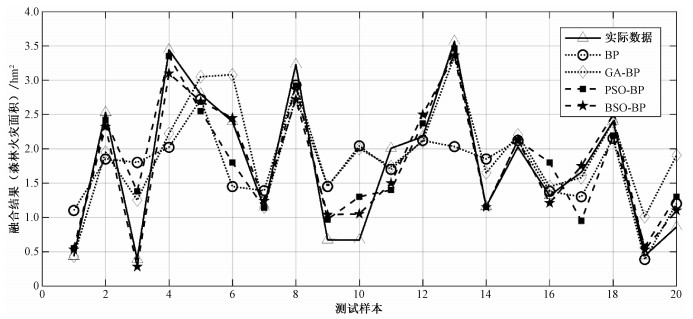
| 图 2 融合结果比较 Fig. 2 Comparison of fusion results | |
4种算法的详细评价指标对比结果如表 3。从表 3可以看出BSO-BP算法在平均相对误差、均方根误差以及拟合优度3个方面都优于其他3种算法。BSO-BP算法和传统BP算法相比,平均相对误差和均方根误差分别减少28%和37.4%。相较于PSO-BP算法,减少了11%的平均相对误差和13.89%的均方根误差。BSO-BP算法克服了BP神经网络易陷入局部最优解的缺陷,增加了粒子群算法的种群搜索空间多样性,解决了粒子群算法早熟收敛的问题,因此BSO-BP算法相比其他算法有更好的数据融合效果。
|
|
表 3 融合误差对比 Table 3 Comparison of fusion error |
2) 迭代收敛对比
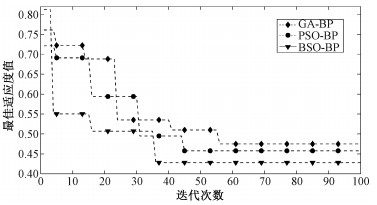
为测试BSO-BP算法的收敛性能,选择与GA-BP算法和PSO-BP算法进行仿真对比。图 3为迭代收敛优化对比结果,由图可知,GA-BP算法经过大约55次迭代收敛至最佳适应度值附近,PSO-BP算法大约经过46次迭代能收敛至全局最优解附近,而BSO-BP算法只需大约35次迭代,相比GA-BP和PSO-BP算法收敛速度提高,并且能寻找到更优的最佳适应度值。结果表明,将天牛须搜索算法中的天牛搜索行为增加到粒子群算法的粒子特性中能有效地增加寻优空间,避免陷入局部最优解,提高收敛速度和寻优性能,可以高效地优化BP神经网络的初始参数。
|
Download:
|
| 图 3 算法迭代收敛对比 Fig. 3 Comparison of iterative convergence among algorithms | |
3) 网络生命周期
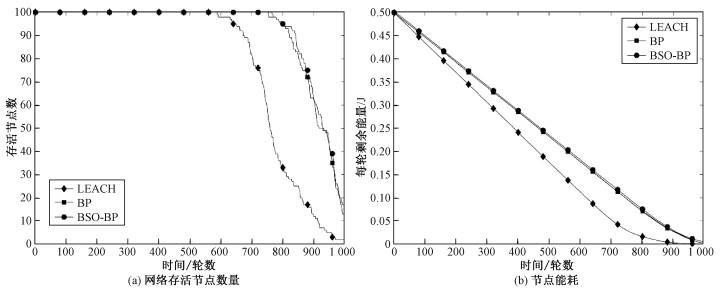
WSN中传感器节点能量有限,若监测区域出现单个或多个传感器节点能量耗尽或剩余能量不足以支持节点正常工作的情况,会导致监测盲区增多,获取的监测数据不准确,危险系数上升。网络生命周期在不同文献中有不同定义,文献[18]定义无线传感网络生命周期为目标监测区域内覆盖率到达容忍下限值的时间,文献[19]定义网络生命周期为网络开始到节点能量全部消耗完的时间。本文采用文献[18]的定义,参考文献[11]和实际经验设定网络存活节点低于85%时,覆盖率达到容忍值,此时的数据可靠性下降,需要补充传感器节点能量。图 4(a)为各算法网络生命周期对比结果,可以看出在存活节点到达85%的阈值时,LEACH协议网络运行至700轮左右,BSO-BP算法和BP算法网络运行至830轮左右,相比LEACH协议延长18.5%,这是由于BSO-BP算法和BP算法对监测数据进行了融合,减少了数据传输量,降低节点能耗,有效地延长了网络生命周期。图 4(b)为节点能耗对比,可以看出,LEACH协议节点能耗明显高于BSO-BP算法和BP算法,而BSO-BP算法和BP算法的节点能耗和网络生命周期大致相当,这是因为两者的BP神经网络结构相同并且网络的构建和训练都是在基站节点进行,数据融合的输出维度一致。
|
Download:
|
| 图 4 网络存活节点数量和节点能耗 Fig. 4 The number of alive nodes and the energy consumption of the node | |
针对无线传感网BP神经网络数据融合算法存在对初始参数敏感、易陷入局部最优解的缺陷,本文提出基于改进粒子群的BP神经网络WSN数据融合算法(BSO-BP)。算法利用天牛须搜索(BAS)算法对粒子群算法进行改进,利用改进后的粒子群算法优化BP神经网络的初始权值和阈值,引入WSN数据融合中,簇首节点通过优化训练后的BP神经网络对采集数据进行特征提取,将融合后的数据发送至汇聚节点。与传统BP算法和PSO-BP算法进行对比,该算法能有效地提高融合精度和收敛速度,减少冗余数据传输,延长网络生命周期。
| [1] |
Lin D, Wang Q, Lin D, et al. An energy-efficient clustering routing protocol based on evolutionary game theory in wireless sensor networks[J]. International Journal of Distributed Sensor Networks, 2015, 2015: 1-12. |
| [2] |
Heinzelman W R, Chandrakasan A, Balakrishnan H. Energy-efficient communication protocol for wireless microsensor networks[C]//Proceedings of the 33rd Annual Hawaii International Conference on System Sciences. Hawaii: IEEE, 2000: 1-10.
|
| [3] |
孙凌逸, 黄先祥, 蔡伟, 等. 基于神经网络的无线传感器网络数据融合算法[J]. 传感技术学报, 2011, 24(1): 122-127. |
| [4] |
Boyinbode O, Le H, Mbogho A, et al. A survey on clustering algorithms for wireless sensor networks[C]//2010 IEEE 13th International Conference on Network-based Information Systems. Takayama: IEEE, 2010: 358-364.
|
| [5] |
成瑜娟, 张敏洪. 感应半径可调的无线传感器网络生命周期的研究[J]. 中国科学院研究生院学报, 2011, 28(6): 768-775. |
| [6] |
李兆祥.无线传感器网络数据融合的算法研究[D].武汉: 武汉理工大学, 2011.
|
| [7] |
赵亚光.基于蚁群算法和BP神经网络的WSN数据融合算法研究[D].昆明: 云南大学, 2013.
|
| [8] |
陈秋红, 郭猛. 基于PSO-BP的无线传感器网络数据融合算法研究[J]. 计算机测量与控制, 2014, 22(4): 1212-1214. |
| [9] |
Kennedy J, Eberhart R. Particle swarm optimization[C]//Proceedings of ICNN'95-International Conference on Neural Networks. Perth: IEEE, 1995: 1942-1948.
|
| [10] |
Wang T, Yang L, Liu Q. Beetle swarm optimization algorithm: theory and application[J]. arXiv preprint arXiv: 1808.00206, 2018.
|
| [11] |
胡强, 王海涛, 底楠, 等. 无线传感网中一种智能数据融合算法的实现及仿真分析[J]. 传感技术学报, 2018, 31(2): 283-288. |
| [12] |
Jiang X Y, Li S. BAS: beetle antennae search algorithm for optimization problems[J/OL]. International Journal of Robotics and Control, 2018[2019-03-05]. https: //arxiv.org/pdf/1710.10724.pdf.
|
| [13] |
刘杨, 田学锋, 詹志辉. 粒子群优化算法惯量权重控制方法的研究[J]. 南京大学学报(自然科学版), 2011, 47(4): 364-371. |
| [14] |
张震, 魏鹏, 李玉峰, 等. 改进粒子群联合禁忌搜索的特征选择算法[J]. 通信学报, 2018, 39(12): 60-68. |
| [15] |
焦李成, 杨淑媛, 刘芳, 等. 神经网络七十年:回顾与展望[J]. 计算机学报, 2016, 39(8): 1697-1716. |
| [16] |
段大高, 谢永恒, 盖新新, 等. 基于神经网络的微博虚假信息识别模型[J]. 信息网络安全, 2017, 17(9): 134-137. |
| [17] |
胡向东, 李秋实. 基于人工鱼群算法优化神经网络的WSN数据融合[J]. 重庆邮电大学学报(自然科学版), 2018, 30(5): 614-619. |
| [18] |
Ishizuka M, Aida M. Performance study of node placement in sensor network[C]//24th International Conference on Distributed Computing Systems. Hachioji: IEEE, 2004: 598-603.
|
| [19] |
Guidoni D L, Boukerche A, Villas L A, et al. A tree-based approach to design heterogeneous sensor networks based on small world concepts[C]//2011 IEEE 36th Conference on Local Computer Networks. Bonn: IEEE, 2011: 666-672.
|
 2020, Vol. 37
2020, Vol. 37 


