多向中继信道模型(multiway relay channel, mRC)^[1-2]主要有以下两种数据交换模型：成对的数据交换模型，即两个用户相互交换信息；完整的数据交换模型，即一个用户将相同的信息广播给多个用户。此模型在实际应用中普遍存在。例如，社交网络中，多个小组的用户希望在同组中共享文件。由于网络中每个节点配置有多根天线，多输入多输出(multiple input multiple output, MIMO)mRC可以极大地提高复用增益。但是由于中继信道的信道容量难以刻画^[3]，所以很多工作集中在模型自由度(degree of freedom, DoF)的分析上，即高信噪比下的性能特点。简单说，网络的DoF是网络中可以支持的独立数据流数目^[4]。

目前，国内外学者对于mRC的DoF分析已经有了一些结果，但是大多数研究集中在成对的数据交换模型^[5-9]中，尤其是基于成对数据交换模型的一种特殊模型，Y-信道模型^[10-11]。并且由于成对数据交换模型上行和下行链路是对称的，所以大多数工作集中在全双工通信模型。相比来说，对于完整数据交换模型的分析相对较少，并且由于完整数据交换模型上行和下行链路是非对称的，分析半双工通信下系统可达的DoF也非常重要。文献[12]给出全双工通信下有多个用户集群的完整数据交换模型一个可达的DoF。对于有多个用户集群，每个用户集群中有多个用户的信道模型，通过设计信号对齐，给出此模型一个一般化的结果。文献[13]分析半双工通信下有一个用户集群，用户集群中有多个用户的完整数据交换模型的DoF。此模型中，对于每一个用户来说，没有来自于其他用户集群的干扰信号。作者推出此模型在半双工通信下的DoF容量，即验证了此模型的割集上界是可达的。并且当上行和下行时隙相等时，作者将半双工通信的结果推广到全双工通信。由于有多个用户集群的完整数据交换模型比较复杂，直接分析其DoF比较困难，文献[14]结合优化算法^[15]推出一个优化的结果。但是此算法仅对全双工通信有效，对于半双工通信下的DoF仍然未知。

本文研究半双工通信下两个用户集群，每个用户集群中多个用户的MIMO mRC在完整数据交换模型下可达的DoF。同时对于全双工通信，假设每个结点可以进行自干扰消除。所以当上行和下行时隙相等时，半双工通信的结果可以推广到全双工通信，即此时全双工通信的结果是半双工通信的2倍。将半双工通信下上行和下行时隙相等的结果推广到全双工通信，并且验证该信号对齐方案可以达到全双工通信目前最优的结果。

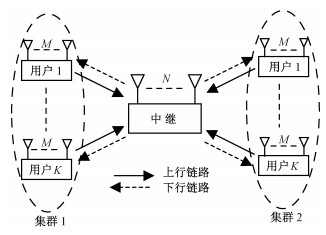
1 系统模型 1.1 信道模型

本文考虑半双工通信^①的MIMO mRC。该信道包含L个用户集群，每个集群包含K个用户。考虑完整数据交换模型，即每个用户希望与同一个集群中其他所有用户交换信息。考虑对称的天线配置，假设中继端有N个天线，每个用户端有M个天线。由于集群数目较多时模型较为复杂，本文只考虑L=2，即有两个用户集群的情况，模型见图 1。将集群j中的用户k定义为Γ_jk，其中$j \in {I_L} \buildrel \Delta \over = \{ 1, 2\} $，$k \in {I_L} \buildrel \Delta \over = \{ 1, \cdots , k\} $。假设在第t个时隙，用户Γ_jk到中继的信道矩阵为${\mathit{\boldsymbol{H}}_{jk}}(t) \in {\mathbb{C}^{N \times M}}$，中继到用户Γ_jk的信道矩阵为$\mathit{\boldsymbol{G}}_{jk}^{\rm{T}}(t) \in {\mathbb{C}^{M \times N}}$。假设H_jk(t)和G_jk^T(t)的所有元素独立且服从连续分布，即信道矩阵行满秩或列满秩。同时假设对于所有结点，信道状态信息是已知的。

① 后文中，令上行和下行链路时隙相同，将此时半双工通信的结果推广到全双工通信系统，得到全双工通信系统可达的DoF。

考虑物理层网络编码^[16]，整个数据交换包含两个传输链路，即上行链路和下行链路。上行链路所有用户将信号发送给中继, 下行链路中继将信号广播给所有用户。假设上行和下行链路分别包含T_u和T_d个时隙，则在第t个时隙，信道模型可以表示为

$ {\mathit{\boldsymbol{y}}_{\rm{R}}}(t) = \sum\limits_{j = 1}^2 {\sum\limits_{k = 1}^K {{\mathit{\boldsymbol{H}}_{jk}}} } (t){\mathit{\boldsymbol{x}}_{jk}}(t) + {\mathit{\boldsymbol{z}}_{\rm{R}}}(t), $

(1)

$ {\mathit{\boldsymbol{y}}_{jk}}(t) = \mathit{\boldsymbol{G}}_{jk}^{\rm{T}}(t){\mathit{\boldsymbol{x}}_{\rm{R}}}(t) + {\mathit{\boldsymbol{z}}_{jk}}(t), $

(2)

式中：$\mathit{\boldsymbol{x}}_{jk}^{}(t) \in {\mathbb{C}^{M \times 1}}$和$\mathit{\boldsymbol{y}}_{jk}^{}(t) \in {\mathbb{C}^{M \times 1}}$分别表示用户Γ_jk发送和接收的信息; $\mathit{\boldsymbol{x}}_{\rm{R}}^{}(t) \in {\mathbb{C}^{N \times 1}}$和$\mathit{\boldsymbol{y}}_{\rm{R}}^{}(t) \in {\mathbb{C}^{N \times 1}}$分别表示中继发送和接收的信息; z_R(t)和z_jk(t)分别表示中继端和用户Γ_jk端的加性高斯白噪声，其元素独立且服从高斯分布CN(0, σ²)。

由于上行和下行链路分别包含T_u和T_d个时隙，上述信道模型简化为

$ {\mathit{\boldsymbol{y}}_{\rm{R}}} = \sum\limits_{j = 1}^2 {\sum\limits_{k = 1}^K {{\mathit{\boldsymbol{H}}_{jk}}} } {\mathit{\boldsymbol{x}}_{jk}} + {\mathit{\boldsymbol{z}}_{\rm{R}}}, $

(3)

$ {\mathit{\boldsymbol{y}}_{jk}} = \mathit{\boldsymbol{G}}_{jk}^{\rm{T}}{\mathit{\boldsymbol{x}}_{\rm{R}}} + {\mathit{\boldsymbol{z}}_{jk}}, $

(4)

式中：y_R=[y_R^T(1), …, y_R^T(T_u)]^T，x_jk=[x_jk^T(1), …, x_jk^T(T_u)]^T，z_R=[z_R^T(1), …, z_R^T(T_u)]^T，x_R=[x_R^T(1), …, x_R^T(T_d)]^T，y_jk=[y_jk^T(1), …, y_jk^T(T_d)]^T，

$ \begin{array}{l} {\mathit{\boldsymbol{H}}_{jk}} = {\mathop{\rm diag}\nolimits} \left\{ {{\mathit{\boldsymbol{H}}_{jk}}(1), \cdots , {\mathit{\boldsymbol{H}}_{jk}}\left( {{T_{\rm{u}}}} \right)} \right\}\\ \;\;\;\;\;\; = \left( {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{H}}_{jk}}(1)}& \cdots &\mathit{\boldsymbol{0}}\\ \vdots & \ddots & \vdots \\ \mathit{\boldsymbol{0}}& \cdots &{{\mathit{\boldsymbol{H}}_{jk}}\left( {{T_{\rm{u}}}} \right)} \end{array}} \right) \end{array} $

G_jk^T=diag{G_jk^T(1), …, G_jk^T(T_d)}。用户Γ_jk和中继端发送的信号分别满足功率限制$\frac{1}{T}{\rm{tr(}}{\mathit{\boldsymbol{x}}_{jk}}\mathit{\boldsymbol{x}}_{jk}^{\rm{H}}{\rm{)}} \le {P_{jk}}$, j∈I_L, k∈I_K和$\frac{1}{T}{\rm{tr(}}{\mathit{\boldsymbol{x}}_{\rm{R}}}\mathit{\boldsymbol{x}}_{\rm{R}}^{\rm{H}}{\rm{)}} \le {P_{\rm{R}}}$。其中P_jk和P_R分别为用户端和中继端最大的发送功率。

1.2 用户端和中继端的预处理

假设用户Γ_jk发送信号W_jk给同一集群j中其他所有用户，并且希望收到来自集群j中其他所有用户发送的信号W_jk′，其中k′∈I_K \{k}，本文中符号A\B表示从集合A中排除集合B。

首先考虑上行链路，假设${{\mathit{\boldsymbol{x'}}}_{jk}} \in {\mathbb{C}^{{d_{\rm{u}}}{T_{\rm{u}}} \times 1}}$为用户Γ_jk发送的码字矩阵, 它与W_jk一一对应。其中d_u表示每个时隙W_jk被编码为一个d_u×1的码字，即每个用户每个时隙发送d_u个独立数据流。假设${\mathit{\boldsymbol{U}}_{jk}} \in {\mathbb{C}^{M{T_{\rm{u}}} \times {d_{\rm{u}}}{T_{\rm{u}}}}}$为相应的预编码矩阵, 那么

$ {\mathit{\boldsymbol{x}}_{jk}} = {\mathit{\boldsymbol{U}}_{jk}}{{\mathit{\boldsymbol{x'}}}_{jk}}. $

(5)

接下来考虑中继端的处理。为了描述方便，引入以下符号：

$ {\mathit{\boldsymbol{M}}_j} = \left[ {{\mathit{\boldsymbol{H}}_{j1}}{\mathit{\boldsymbol{U}}_{j1}}, \cdots , {\mathit{\boldsymbol{H}}_{jk}}{\mathit{\boldsymbol{U}}_{jk}}} \right], j \in {I_L}, $

(6a)

$ {\mathit{\boldsymbol{M}}_{j\bar k}} = {\mathit{\boldsymbol{M}}_j}\backslash \{ {\mathit{\boldsymbol{H}}_{jk}}{\mathit{\boldsymbol{U}}_{jk}}\} , $

(6b)

$ \mathit{\boldsymbol{M = }}{\rm{[}}{\mathit{\boldsymbol{M}}_1}{\rm{, }}{\mathit{\boldsymbol{M}}_2}{\rm{], }} $

(6c)

$ {\mathit{\boldsymbol{M}}_{\bar j}} = \mathit{\boldsymbol{M}}\backslash \mathit{\boldsymbol{M, }}j \in {I_L}. $

(6d)

中继端接收到来自于两个集群的用户信息。对于集群j的用户来说，集群${\bar j}$，$\bar j \in {I_L}\backslash \{ j\} $的用户发送的信号为干扰信号。为解出集群j的信号，中继需要从y_R中提取出与干扰集群的信号正交的信号分量。也就是说，对于集群j，存在投影矩阵${\mathit{\boldsymbol{P}}_j} \in {\mathbb{C}^{N{T_{\rm{u}}} \times N{T_{\rm{u}}}}}$，将y_R投影到${\rm{null(}}\mathit{\boldsymbol{M}}_{\bar j}^{\rm{T}})$, 即

$ {\mathit{\boldsymbol{P}}_j}{\mathit{\boldsymbol{y}}_{\rm{R}}} = {\mathit{\boldsymbol{P}}_j}{\mathit{\boldsymbol{M}}_j}\mathit{\boldsymbol{x}}_j^\prime + {\mathit{\boldsymbol{P}}_j}{\mathit{\boldsymbol{z}}_{\rm{R}}}, $

(7)

其中x′_j=[x′_j1, …, x′_jK]^T。式中，通过投影，集群j′≠j中的信号被去除了。

接下来考虑下行链路。和前面类似，引入N_j=[G_j1V_j1, …, G_jKV_jK]，N=[N₁, N₂]和${\mathit{\boldsymbol{N}}_{\bar j}} = \mathit{\boldsymbol{N}}\backslash {\mathit{\boldsymbol{N}}_j}$。其中${\mathit{\boldsymbol{V}}_{jk}} \in {\mathbb{C}^{M{T_{\rm{d}}} \times {d_{\rm{d}}}{T_{\rm{d}}}}}$是用户Γ_jk的接收处理矩阵，d_d表示每个用户每个时隙接收d_d个独立数据流。令${\mathit{\boldsymbol{W}}_j} \in {\mathbb{C}^{N{T_{\rm{d}}} \times N{T_{\rm{d}}}}}$表示将向量投影到${\rm{null(}}\mathit{\boldsymbol{N}}_{\bar j}^{\rm{T}})$的投影矩阵。

考虑半双工通信，上行和下行链路时隙分配允许不同。假设$\mathit{\boldsymbol{F}} \in {\mathbb{C}^{N{T_{\rm{d}}} \times N{T_{\rm{u}}}}}$表示中继端将上行链路接收的T_u个时隙的信号在下行链路使用T_d个时隙发送给每个用户。

因此，中继端发送的信号为

$ {\mathit{\boldsymbol{x}}_{\rm{R}}} = \alpha \sum\limits_{j = 1}^L {\mathit{\boldsymbol{W}}_j^{\rm{T}}} \mathit{\boldsymbol{F}}{\mathit{\boldsymbol{P}}_j}{\mathit{\boldsymbol{y}}_{\rm{R}}}, $

(8)

式中：α为中继端满足功率限制的缩放因子。

最终，用户Γ_jk收到的信号为

$ \mathit{\boldsymbol{V}}_{jk}^{\rm{T}}{\mathit{\boldsymbol{y}}_{jk}} = \alpha \mathit{\boldsymbol{V}}_{jk}^{\rm{T}}\mathit{\boldsymbol{G}}_{jk}^{\rm{T}}\sum\limits_{{j^\prime } = 1}^L {\mathit{\boldsymbol{W}}_j^{{\rm{T}}\prime }} \mathit{\boldsymbol{FP}}_j^\prime {\mathit{\boldsymbol{y}}_{\rm{R}}} + \mathit{\boldsymbol{V}}_{jk}^{\rm{T}}{\mathit{\boldsymbol{z}}_{jk}} $

(9a)

$ = \alpha \mathit{\boldsymbol{V}}_{jk}^{\rm{T}}\mathit{\boldsymbol{G}}_{jk}^{\rm{T}}\mathit{\boldsymbol{W}}_j^{\rm{T}}\mathit{\boldsymbol{F}}{\mathit{\boldsymbol{P}}_j}(\sum\limits_{{k^\prime } = 1}^K {{\mathit{\boldsymbol{H}}_{j{k^\prime }}}} {\mathit{\boldsymbol{U}}_{jk}}{\mathit{\boldsymbol{x}}^\prime }_{j{k^\prime }} + {\mathit{\boldsymbol{z}}_{\rm{R}}}) +\\ \mathit{\boldsymbol{V}}_{jk}^{\rm{T}}{\mathit{\boldsymbol{z}}_{jk}}. $

(9b)

收到V_jk^Ty_jk后，用户Γ_jk解出信号W_jk′，记为$\mathit{\boldsymbol{\hat W}}_{jk}^{k'}$，其中k′≠k。

从式(9)看出，集群j中的其他用户到用户Γ_jk的等效信道为$\mathit{\boldsymbol{V}}_{jk}^{\rm{T}}\mathit{\boldsymbol{G}}_{jk}^{\rm{T}}\mathit{\boldsymbol{W}}_j^{\rm{T}}\mathit{\boldsymbol{F}}{\mathit{\boldsymbol{P}}_j}{\mathit{\boldsymbol{M}}_{j\bar k}}$。此等效信道可以看作上行等效信道${\mathit{\boldsymbol{P}}_j}{\mathit{\boldsymbol{M}}_{j\bar k}}$，中继时隙分配矩阵F和下行等效信道$\mathit{\boldsymbol{V}}_{jk}^{\rm{T}}\mathit{\boldsymbol{G}}_{jk}^{\rm{T}}\mathit{\boldsymbol{W}}_j^{\rm{T}}$的乘积。注意文献[12]将集群j中其他用户Γ_jk′到用户Γ_jk的等效信道看作两个对称等效信道的乘积。由于本文考虑半双工通信，F矩阵的引入使得上行/下行链路不再对称。因此我们考虑对上行/下行链路分别设计信号对齐。

1.3 自由度

由于MIMO mRC的香农容量很难刻画，因此本文主要分析网络的DoF。简单来说，网络的DoF是网络中可以支持的独立信息流数目。

假设T=T_u+T_d表示一次信息传输使用的总时隙^①，W_jk携带的信息速率为R_jk。如果T→∞时，对于任意k′∈I_K\{k}，$\mathit{\boldsymbol{\hat W}}_{jk}^{k'} \ne {\mathit{\boldsymbol{W}}_{jk'}}$总是0，称用户Γ_jk达到总信息速率${C_{jk}} = \sum\nolimits_{k' = 1, k' \ne k}^K {{R_{jk'}}} $。假设P_jk=β_jkP, j∈I_L, k∈I_K; P_R=βP，其中β_jk和β均为常系数。接下来，定义系统可达到的总DoF为

① 此时考虑半双工通信，后文中令T_u+T_d=T，将结果推广到全双工通信。

$ {d_{{\rm{sum}}}} \buildrel \Delta \over = \mathop {{\rm{lim}}}\limits_{P \to \infty } \frac{{\sum\nolimits_{j = 1}^L {\sum\nolimits_{k = 1}^K {{C_{jk}}} } (P)}}{{{\rm{log}}P}}, $

(10)

式中：C_jk(P)单位是bit，log表示对数以2为底，同时，定义每个用户可达到的DoF为

$ {d_{{\rm{ user }}}} \buildrel \Delta \over = \frac{1}{{KL}}{d_{{\rm{ sum }}}}. $

(11)

式中：d_user表示用户收到的独立的数据流数目。

注意：考虑全双工通信时，此信道模型的一个割集上界^[12]为d_sum≤min（KLM, KN），即平均每个用户收到的DoF为

$ {d_{{\rm{ user }}}} \le {\rm{min}}\left( {M, \frac{N}{L}} \right). $

(12)

2 问题讨论 2.1 初期讨论

分别对上行和下行链路进行分析。

上行链路集群j中其他用户到用户Γ_jk的等效信道矩阵为${\mathit{\boldsymbol{P}}_j}{\mathit{\boldsymbol{M}}_{j\bar k}}$，其中P_j表示将向量投影到${\rm{null(}}\mathit{\boldsymbol{M}}_{\bar j}^{\rm{T}})$的投影矩阵。${\mathit{\boldsymbol{P}}_j}{\mathit{\boldsymbol{M}}_{j\bar k}}$与P_jM_j的差别在于用户Γ_jk已知自己发送的信号。对于集群j，每个用户发送d_uT_u个独立数据流，集群中共有Kd_uT_u个数据流，但是考虑到每个用户接收到同一个集群的数据流后可以去除自己发送的d_uT_u个数据流，集群j在中继端只需占用(K－1)d_uT_u个无干扰的空间维度。所以，上行链路设计信号对齐，满足rank(P_jM_j)≥ (K－1)d_uT_u。

下行链路集群j中其他用户到用户Γ_jk的等效信道矩阵为$\mathit{\boldsymbol{V}}_{jk}^{\rm{T}}\mathit{\boldsymbol{G}}_{jk}^{\rm{T}}\mathit{\boldsymbol{W}}_j^{\rm{T}}$，其中W_j表示将向量投影到${\rm{null(}}\mathit{\boldsymbol{N}}_{\bar j}^{\rm{T}})$的投影矩阵。对于集群j，每个用户接收到d_dT_d个独立数据流。所以，下行链路中继端只需为每个集群发送d_dT_d维度的无干扰信号。设计信号对齐，满足${\rm{rank(}}\mathit{\boldsymbol{V}}_{jk}^{\rm{T}}\mathit{\boldsymbol{G}}_{jk}^{\rm{T}}\mathit{\boldsymbol{W}}_j^{\rm{T}}{\rm{)}} \ge {d_{\rm{d}}}{T_{\rm{d}}}$。

结合以上对上行和下行链路的分析，如果设计上行预处理矩阵U_jk和下行接收处理矩阵V_jk满足

$ { {\rm{rank}} ({\mathit{\boldsymbol{P}}_j}{\mathit{\boldsymbol{M}}_j}) \ge (K - 1){d_{\rm{u}}}{T_{\rm{u}}}, } $

(13a)

$ { {\rm{rank}} (\mathit{\boldsymbol{V}}_{jk}^{\rm{T}}\mathit{\boldsymbol{G}}_{jk}^{\rm{T}}\mathit{\boldsymbol{W}}_j^{\rm{T}}) \ge {d_{\rm{d}}}{T_{\rm{d}}}, } $

(13b)

则用户Γ_jk的自由度取决于上行链路集群j中其他所有用户发送的数据流数目(K－1)d_uT_u和下行链路它能接收到的数据流数目d_dT_d，即每个用户可达的DoF为

$ {d_{{\rm{ user }}}} = \frac{1}{T}{\rm{min}}\{ (K - 1){d_{\rm{u}}}{T_{\rm{u}}}, {d_{\rm{d}}}{T_{\rm{d}}}\} . $

(13c)

为描述方便，后文分别称d_u和d_d为上行和下行链路每个用户可达的DoF。

由于我们的信号对齐方案不考虑多个时隙之间的信号对齐，所以接下来考虑单个时隙下(此时T_u=T_d=1)如何设计信号对齐，使得d_u和d_d最大。

2.2 相关引理和定义

对上行和下行链路设计信号对齐时，均使用了天线禁用技术和角点的概念^[12]。接下来以上行链路为例对天线禁用技术进行介绍，并且对角点进行定义。

性质1  每个用户的上行和下行链路的DoF均受中继端天线N和用户端天线M的限制，也就是说，d_u和d_d均为M和N的函数，即d_u=Nf(M/N)，${d_{\rm{d}}} = N\tilde f(M/N)$，其中f(·)，$\tilde fD( \cdot )$均为M/N的函数。

引理1(天线禁用技术)  对于所考虑的MIMO mRC，假设上行链路d_u=Nf(M/N)在一个固定的天线配置(M=M₀, N=N₀)时，d_u=d₀可达。那么通过在用户端禁用M－M₀根天线，(x=M/N₀, y=d_u)在线段x∈[M₀/N₀, ∞)，y=d₀上的每个点可达；通过在中继端禁用N₀-(MN₀/M₀)根天线，(x=M/N₀, y=d_u)在线段x∈(0, M₀/N₀], y=(d₀N₀/M₀)x上的每个点可达。

通过天线禁用技术，只需要给出可达DoF曲线中特定的点，即可得到整个可达DoF曲线。接下来，称这些特定点为角点，并给出以下定义。

定义1(角点)  已知上行链路一个可达的DoF曲线d_u=Nf(M/N)，固定中继端天线N=N₀。对于可达DoF曲线中某一点(M₀/N₀, d₀)，如果当M>M₀时，(M /M₀, d₀M/M₀)不可达；并且当M < M₀时，(M/N₀, d₀)时不可达，则称(M₀/N₀, d₀)为可达DoF曲线上的一个角点。

以上对天线禁用技术的描述和角点的定义同样适用于下行链路。接下来，只需找到上行和下行链路所有的角点，并且结合天线禁用技术，即可得上行和下行链路的可达DoF，即d_u和d_d。为描述方便，定义g函数

$ {g_{(a, b)}}(x) = \left\{ {\begin{array}{*{20}{l}} {\frac{{bx}}{a}, }&{{\rm{ 当 }}x < a{\rm{ 时 }}}\\ {b, }&{{\rm{ 当 }}x \ge a{\rm{ }}{\kern 1pt} {\kern 1pt} {\rm{时 }}} \end{array}} \right., $

(14)

式中a和b是常系数。

3 信号对齐 3.1 上行链路信号对齐

上行链路设计信号对齐满足单个时隙下rank(P_jM_j)≥(K－1)d_u。接下来，给出候选角点(M/N, d_u)，并结合候选角点给出相应的可达DoF。

引理2  对于两个用户集群，每个集群K个用户的M×NMIMO mRC，当数据交换模型为完整数据交换模型时，对于上行链路以下候选角点(M/N, d_u)是可达的：

$ {\rm{角点}}({\rm{U1}}){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{M}{N} = \frac{1}{{2K - 1}}, {d_{\rm{u}}} = \frac{N}{{2K - 1}}; $

(15a)

$ {\rm{角点}}({\rm{U2}}){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{M}{N} = \frac{{2K - 1}}{{2K(K - 1)}}, {d_{\rm{u}}} = \frac{N}{{2(K - 1)}}. $

(15b)

定义集合I包含式(15)中所有候选角点(M/N, d_u)，则上行链路每个用户可达的一个DoF为

$ {d_u} = \mathop {{\rm{max}}}\limits_{(a, b) \in I} {g_{(a, b)}}\left( {\frac{M}{N}} \right). $

(16)

证明  已知候选角点，根据天线禁用技术，可以得到式(16)。接下来设计信号对齐证明角点(U1)和(U2)满足rank(P_jM_j)≥(K－1)d_u。

1) 对于角点(U1), 当M/N=1/(2K-1)时，假设$\mathit{\boldsymbol{H}} = \left[ {{\mathit{\boldsymbol{H}}_{11}}, \cdots , {\mathit{\boldsymbol{H}}_{1K}}, {\mathit{\boldsymbol{H}}_{21}}, \cdots , {\mathit{\boldsymbol{H}}_{2K}}} \right] \in {\mathbb{C}^{N \times 2KM}}$，由于信道的随机性，null(H)以概率1是2KM-N维。因此存在满秩矩阵${\mathit{\boldsymbol{U}}_{jk}} \in {\mathbb{C}^{M \times (2KM - N)}}$, j∈I_L, k∈I_K满足

$ \sum\limits_{j = 1}^2 {\sum\limits_{k = 1}^K {{\mathit{\boldsymbol{H}}_{jk}}} } {\mathit{\boldsymbol{U}}_{jk}} = \mathit{\boldsymbol{0}}\mathit{\boldsymbol{.}} $

(17)

此时，每个用户发送d_u =2KM-N=N/(2K-1)个数据流。在中继端，每个集群的信号占据KN/(2K-1)个信号维度，所以另外一个集群占据N-KN/(2K-1)个无干扰的信号维度，即${\rm{rank(}}{\mathit{\boldsymbol{P}}_j}{\mathit{\boldsymbol{M}}_j}{\rm{) = dim(null(}}\mathit{\boldsymbol{M}}_{\bar j}^{\rm{T}}){\rm{) = }}N{\rm{ - }}KN/(2K - 1) = (K - 1){d_{\rm{d}}}$。

2) 对于角点(U2)，当M/N=(2K-1)/(2K(K-1))时，假设${\mathit{\boldsymbol{H}}_j} = [{\mathit{\boldsymbol{H}}_{j1}}, \cdots , {\mathit{\boldsymbol{H}}_{jk}}] \in {^{N \times KM}}$, j∈I_L。由于信道的随机性，null(H_j)以概率1是KM-N维。因此存在${\mathit{\boldsymbol{U}}_{jk}} \in {\mathbb{C}^{M \times (KM - N)}}$, k∈I_K满足

$ \sum\limits_{k = 1}^K {{\mathit{\boldsymbol{H}}_{jk}}} {\mathit{\boldsymbol{U}}_{jk}} = \mathit{\boldsymbol{0}}, {\rm{ 其中 }}j = 1, 2. $

(18)

此时，每个用户发送d_u =KM-N=N/(2K-2)个数据流。中继端，每个集群的信号占据(K-1) d_u =N/2维，所以另外一个集群占据N-N/2个无干扰的信号维度，即${\rm{rank(}}{\mathit{\boldsymbol{P}}_j}{\mathit{\boldsymbol{M}}_j}{\rm{) = dim(null(}}\mathit{\boldsymbol{M}}_{\bar j}^{\rm{T}}){\rm{) = }}N{\rm{ - }}N/2 = (K - 1){d_{\rm{u}}}$。证毕。

3.2 下行链路信号对齐

下行链路设计信号对齐满足单个时隙下${\rm{rank(}}\mathit{\boldsymbol{V}}_{jk}^{\rm{T}}\mathit{\boldsymbol{G}}_{jk}^{\rm{T}}\mathit{\boldsymbol{W}}_j^{\rm{T}}{\rm{)}} = {\rm{rank(}}\mathit{\boldsymbol{W}}_j^{}\mathit{\boldsymbol{G}}_{jk}^{}\mathit{\boldsymbol{V}}_{jk}^{}{\rm{)}} \ge {d_{\rm{d}}}$。接下来，给出候选角点(M/N, d_d)，并结合候选角点给出相应的可达DoF。

引理3   对于两个用户集群，每个集群K个用户的M×NMIMO mRC，当数据交换模型为完整数据交换模型时，下行链路以下候选角点(M/N, d_d)是可达的：

$ {\rm{角点}}({\rm{D1}}){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{M}{N} = \frac{1}{{K + 1}}, {d_{\rm{d}}} = \frac{N}{{K + 1}}; $

(19a)

$ \begin{array}{l} {\rm{角点}}({\rm{D2}}){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{M}{N} = \frac{1}{m}\left( {1 + \frac{1}{{C_{K - 1}^{m - 1} + C_K^m(m - 1)}}} \right), \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {d_{\rm{d}}} = \left( {\frac{{C_{K - 1}^{m - 1}N}}{{C_{K - 1}^{m - 1} + C_K^m(m - 1)}}} \right), m = 2, \cdots , K - 1; \end{array} $

(19b)

$ \begin{array}{*{20}{c}} {{\rm{角点}}({\rm{D3}}){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{M}{N} = \frac{1}{K}\left( {K - k + \frac{1}{{k + 1}}} \right), }\\ {{d_{\rm{d}}} = \frac{N}{{k + 1}}, k = 1, \cdots , K - 1.} \end{array} $

(19c)

定义集合J包含(19)中所有候选角点(M/N, d_d)，则下行链路每个用户可达的一个DoF为

$ {d_{\rm{d}}} = \mathop {{\rm{max}}}\limits_{(a, b) \in J} {g_{(a, b)}}\left( {\frac{M}{N}} \right). $

(20)

证明  已知候选角点，根据天线禁用技术，可以得到式(20)。接下来我们设计信号对齐证明角点(D1), (D2)和(D3)满足${\rm{rank(}}\mathit{\boldsymbol{W}}_j^{}\mathit{\boldsymbol{G}}_{jk}^{}\mathit{\boldsymbol{V}}_{jk}^{}{\rm{)}} \ge {d_{\rm{d}}}$。

1) 对于角点(D1)，当M/N=1/(K+1)时，不需要设计信号对齐即可满足${\rm{rank(}}\mathit{\boldsymbol{W}}_j^{}\mathit{\boldsymbol{G}}_{jk}^{}\mathit{\boldsymbol{V}}_{jk}^{}{\rm{)}} \ge {d_{\rm{d}}}$。理由如下。假设每个用户Γ_jk端的预处理矩阵${\mathit{\boldsymbol{V}}_{jk}} \in {\mathbb{C}^{M \times M}}$随机，即V_jk满秩。每个用户接收d_d =M=N/(K+1)个独立的数据流。一个集群接收KN/(K+1)个独立数据流。所以中继端发送给另一个集群的无干扰维度为N-KN/(K+1)= d_d。即${\rm{rank(}}\mathit{\boldsymbol{W}}_j^{}\mathit{\boldsymbol{G}}_{jk}^{}\mathit{\boldsymbol{V}}_{jk}^{}{\rm{) = }}N - KN{\rm{/(}}K + 1{\rm{) = }}{d_{\rm{d}}}$。

2) 对于角点(D2)，当$\frac{M}{N} = \frac{1}{m}\left( {1 + \frac{1}{{C_{K - 1}^{m - 1} + C_K^m(m - 1)}}} \right)$, m=2, …, K－1时，M/N>1/m。对于集群j中随机选取的m个用户，记为Γ_jk[1], Γ_jk[2], …, Γ_jk[m]，假设${\mathit{\boldsymbol{G}}_j} = \left[ {{\mathit{\boldsymbol{G}}_{j{k_{[1]}}}}, {\mathit{\boldsymbol{G}}_{j{k_{[2]}}}}, \cdots , {\mathit{\boldsymbol{G}}_{j{k_{[m]}}}}} \right] \in {\mathbb{C}^{N \times mW}}$，由于信道的随机性，null(G_j)以概率1是mM-N维。因此，存在满秩矩阵${\mathit{\boldsymbol{V}}_{j{k_{[t]}}}} \in {\mathbb{C}^{M \times (mM - N)}}$, t∈{1, …, m}满足

$ \sum\limits_{t = 1}^m {{\mathit{\boldsymbol{G}}_{j{k_{[t]}}}}} {\mathit{\boldsymbol{V}}_{j{k_{[t]}}}} = \mathit{\boldsymbol{0}}, {\rm{ 其中 }}j = 1, 2. $

(21)

此时，${\rm{span }}\left( {{\mathit{\boldsymbol{G}}_{j{k_{[1]}}}}{\mathit{\boldsymbol{V}}_{j{k_{[1]}}}}, \cdots , {\mathit{\boldsymbol{G}}_{j{k_{[m]}}}}{\mathit{\boldsymbol{V}}_{j{k_{[m]}}}}} \right) = {\mathop{\rm span}\nolimits} \left( {{\mathit{\boldsymbol{G}}_{j{k_{[1]}}}}{\mathit{\boldsymbol{V}}_{j{k_{[1]}}}}, \cdots , {\mathit{\boldsymbol{G}}_{j{k_{[m - 1]}}}}{\mathit{\boldsymbol{V}}_{j{k_{[m - 1]}}}}} \right)$，并且以概率1是(m－1)(mM－N)维度。由于从K个用户中选取m个用户共有C_K^m种组合，这些组合中包含用户Γ_jk的有C_K－1^m－1种。所以每个用户接收d_d=C_K－1^m－1(mM－N)个独立数据流，一个集群共接收C_K－1^m－1K(mM－N)个独立数据流。在中继端，经过信号对齐这些数据流占用C_K^m(m－1)(mM－N)维度。所以中继端发送给另一个集群的无干扰维度为N-C_K^m(m－1)(mM－N) = C_K－1^m－1(mM－N) = d_d。即${\rm{rank(}}\mathit{\boldsymbol{W}}_j^{}\mathit{\boldsymbol{G}}_{jk}^{}\mathit{\boldsymbol{V}}_{jk}^{}{\rm{) = }}N{\rm{ - }}C_K^m(m - 1)(mN - N) = {d_{\rm{d}}}$。

3) 对于角点(D3)，当$\frac{M}{N} = \frac{1}{K}\left( {K - k + \frac{1}{{k + 1}}} \right), k = 1, \cdots K - 1$时，假设${\mathit{\boldsymbol{G}}_j} = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{G}}_{j1}}}& \cdots &{{{\boldsymbol{G}}_{jk}}}&{{{\boldsymbol{G}}_{j(k + 1)}}}&{}&{\boldsymbol{G}}\\ \vdots & \ddots & \vdots &{}& \ddots &{}\\ {{{\boldsymbol{G}}_{j1}}}& \cdots &{{{\boldsymbol{G}}_{jk}}}&{\boldsymbol{G}}&{}&{{{\boldsymbol{G}}_{jk}}} \end{array}} \right] \in {\mathbb{C}^{(K - k)N \times KM}}$由于信道的随机性，null(G_j)以概率1是KM－(K－k)N=N/(k+1)维度。因此，存在满秩矩阵${\mathit{\boldsymbol{V}}_{jk}} \in {\mathbb{C}^{M \times \frac{N}{{k + 1}}}}$, j∈I_L, k∈I_K满足

$ \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{G}}_{j1}}}& \cdots &{{\mathit{\boldsymbol{G}}_{jk}}}&{{\mathit{\boldsymbol{G}}_{j(k + 1)}}}&{}&\mathit{\pmb{0}}\\ \vdots & \ddots & \vdots &{}& \ddots &{}\\ {{\mathit{\boldsymbol{G}}_{j1}}}& \cdots &{{\mathit{\boldsymbol{G}}_{jk}}}&\mathit{\pmb{0}}&{}&{{\mathit{\boldsymbol{G}}_{jk}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{V}}_{j1}}}\\ \vdots \\ {{\mathit{\boldsymbol{V}}_{jK}}} \end{array}} \right] = \mathit{\pmb{0}}\mathit{\boldsymbol{.}} $

(22)

因此，span(G_j1V_j1, …, G_jKV_jK)=span(G_j1V_j1, …, G_jkV_jk)，并且以概率1是kN/(k+1)维度。此时，每个用户接收d_d=N/(k+1)个独立数据流，经过信号对齐，在中继端一个集群接收的kN/(k+1)个数据流压缩到kN/(k+1)个空间维度。所以中继端发送给另一个集群的无干扰信号维度为N－kN/(k+1)=d_d。即rank(W_jG_jkV_jk)= N－kN/(k+1) = d_d。

证毕。

4 主要结果

引理2和引理3分别给出两个用户集群，每个集群K个用户的MIMO mRC完整数据交换模型上行链路的候选角点(M/N, d_u)∈I和下行链路的候选角点(M/N, d_d)∈J。并根据候选角点给出相应的可达DoF。接下来，结合引理2和引理3，给出此模型一个可达的DoF。

考虑全双工通信，假设每个结点都可以进行自干扰消除，则以上对半双工通信的分析经过调整可以应用于全双工通信。全双工通信和半双工通信主要的区别在于，对于全双工通信，每个结点同时发送和接收信号，因此上行和下行链路总是占用相同的时隙，即T_u=T_d=T。由于引理2和引理3均考虑单个时隙下的信号对齐，由此，令T_u=T_d=T，很容易推出此模型全双工通信下一个可达的DoF。

定理1  对于两个用户集群，每个集群K个用户的M×NMIMO mRC，当考虑完整数据交换模型，并且考虑全双工通信时，每个用户可达到的一个DoF为

$ {d_{{\rm{user}}}} = \mathop {{\rm{max}}}\limits_{(a, b) \in J} {g_{(a, b)}}\left( {\frac{M}{N}} \right). $

(23)

证明   考虑全双工通信，即T_u=T_d=T，由式(13c)，${d_{{\rm{user }}}} = \frac{1}{T}\min \left\{ {(K - 1){d_{\rm{u}}}{T_{\rm{u}}}, {d_{\rm{d}}}{T_{\rm{d}}}} \right\} = \min \left\{ {(K - 1){d_{\rm{u}}}, {d_{\rm{d}}}} \right\}$。结合引理2和引理3，下行链路是网络的瓶颈，得到d_user=d_d。证毕。

令定理1中K=3和K=4，给出以下结论。

推论1   对于L=2，K=3的M×NMIMO mRC，当考虑完整数据交换模型，并且考虑全双工通信时，每个用户可达的一个DoF为

$ {d_{{\rm{user}}}} = \left\{ {\begin{array}{*{20}{l}} {{\rm{min}} \left\{ {M, \frac{N}{4}} \right\}, \;\:{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{M}{N} \le \frac{1}{3}}\\ {{\rm{min}}\left\{ {\frac{{3M}}{4}, \frac{N}{3}} \right\}, \;\:{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{3} < \frac{M}{N} \le \frac{1}{2}}\\ {{\rm{min}}\left\{ {\frac{{2M}}{3}, \frac{{2N}}{5}} \right\}, \;\:\frac{1}{2} < \frac{M}{N} \le \frac{2}{3}}\\ {{\rm{min}}\left\{ {\frac{{3M}}{5}, \frac{N}{2}} \right\}, \;\:{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{2}{3} < \frac{M}{N} < 1} \end{array}} \right.. $

(24)

证明   当K=3时，下行链路存在以下候选角点(M/N, d_d)：

(D1) $\left( {\frac{1}{4}, \frac{N}{4}} \right)$；(D2) $\left( {\frac{3}{5}, \frac{{2N}}{5}} \right)$；

(D3) k=1时, $\left( {\frac{5}{6}, \frac{N}{2}} \right)$；k=2时, $\left( {\frac{4}{9}, \frac{N}{3}} \right)$。

由式(23)得到推论1。

推论2   对于L=2，K=4的M×NMIMO mRC，当考虑完整数据交换模型，并且考虑全双工通信时，每个用户可达的一个DoF为

$ {d_{{\rm{user}}}} = \left\{ {\begin{array}{*{20}{l}} {{\rm{min}}\left\{ {M, \frac{N}{5}} \right\}, \;\:{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{M}{N} \le \frac{1}{4}}\\ {{\rm{min}}\left\{ {\frac{{4M}}{5}, \frac{N}{4}} \right\}, \;\:\frac{1}{4} < \frac{M}{N} \le \frac{1}{3}}\\ {{\rm{min}}\left\{ {\frac{{3M}}{4}, \frac{{3N}}{{11}}} \right\}, \;\frac{1}{3} < \frac{M}{N} \le \frac{5}{{11}}}\\ {{\rm{min}}\left\{ {\frac{{3M}}{5}, \frac{N}{3}} \right\}, \;\:\frac{5}{{11}} < \frac{M}{N} \le \frac{7}{{12}}}\\ {{\rm{min}}\left\{ {\frac{{4M}}{7}, \frac{N}{2}} \right\}, \;\:\frac{7}{{12}} < \frac{M}{N} \le 1} \end{array}} \right.. $

(25)

证明   当K=4时，下行链路存在以下候选角点(M/N, d_d)：

(D1) $\left( {\frac{1}{5}, \frac{N}{5}} \right)$；

(D2) m=2时，$\left( {\frac{5}{9}, \frac{N}{3}} \right)$；m=3时，$\left( {\frac{4}{{11}}, \frac{{3N}}{{11}}} \right)$；

(D3) k=1时，$\left( {\frac{7}{8}, \frac{N}{2}} \right)$；k=2时，$\left( {\frac{7}{{12}}, \frac{N}{3}} \right)$；k=3时，$\left( {\frac{5}{{16}}, \frac{N}{4}} \right)$。

由式(22)得到推论2。

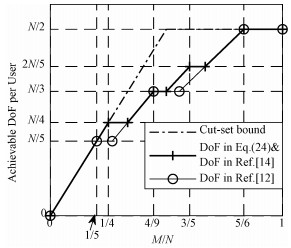
图 2和图 3分别给出L=2, K=3和L=2, K=4全双工通信下系统可达到的DoF。对于L=2, K=3，将全双工通信下的割集上界以及文献[12]，[14]的结果加入进去比较。由于得到2个更优的角点(1/4，N/4)和(3/5，2N/5)，我们的结果在这2个角点附近优于文献[12]中的结果。同时，此结果和文献[14]使用算法优化得到的结果相同。而且这也是目前为止此模型最优的可达DoF。对于L=2, K=4将全双工通信下的割集上界以及文献[12]的结果加入进去比较。此时，得到3个更优的角点(1/5，N/5)，(4/11, 3N/11)和(5/9，N/3)，所以在这几个角点附近我们的结果优于文献[12]中的结果。

注意：考虑全双工通信时，由于网络的瓶颈是下行链路，所以文献[12]中作者考虑上行和下行链路对称设计是足够的, 同时，作者假设每个用户发送一个独立的数据流，则将一个集群的信号尽可能压缩到一维。这和我们下行链路设计信号对齐的要求(13b)是类似的。但是我们在设计下行链路信号对齐时考虑了更多的信号对齐模式，所以得到了更优化的结果。

通过定理1进一步验证了对于完整数据交换模型，下行链路是网络的瓶颈。所以对于半双工通信，通过优化上行和下行链路的时隙可以使系统的DoF进一步提高。

定理2  对于两个用户集群，每个集群K个用户的M×NMIMO mRC，当考虑完整数据交换模型，并且考虑半双工通信时，优化上行和下行链路的时隙分配为

$ \frac{{{T_{\rm{u}}}}}{{{T_{\rm{d}}}}} = \frac{{\mathop {{\rm{max}}}\limits_{(a, b) \in I} {g_{(a, b)}}\left( {\frac{M}{N}} \right)}}{{(K - 1)\mathop {{\rm{max}}}\limits_{(a, b) \in J} {g_{(a, b)}}\left( {\frac{M}{N}} \right)}}. $

(26a)

此时每个用户可达的一个DoF为

$ {d_{{\rm{user}}}} = \frac{{(K - 1){{\left( {\mathop {{\rm{max}}}\limits_{(a, b) \in I} {g_{(a, b)}}\left( {\frac{M}{N}} \right)} \right)}^2}}}{{\mathop {{\rm{max}}}\limits_{(a, b) \in I} {g_{(a, b)}}\left( {\frac{M}{N}} \right) + (K - 1)\mathop {{\rm{max}}}\limits_{(a, b) \in J} {g_{(a, b)}}\left( {\frac{M}{N}} \right)}}. $

(26b)

其中，集合I和集合J分别包含式(15)和式(19)中的角点，g函数定义在式(14)中。

证明   考虑半双工通信，此时T=T_u+T_d则由式(13c)，当(K－1)d_uT_u=d_dT_d时，即$\frac{{{T_{\rm{u}}}}}{{{T_{\rm{d}}}}} = \frac{{{d_{\rm{d}}}}}{{(K - 1){d_{\rm{u}}}}}$时，d_user最大，此时，${d_{{\rm{user }}}}{\rm{ = }}\frac{1}{{{T_{\rm{u}}} + {T_{\rm{d}}}}}\min \left\{ {(K - 1){d_{\rm{u}}}{T_{\rm{u}}}, {d_{\rm{d}}}{T_{\rm{d}}}} \right\} = \frac{{(K - 1){d_{\rm{u}}}{T_{\rm{u}}}}}{{{T_{\rm{u}}} + {T_{\rm{d}}}}} = \frac{{(K - 1){d_{\rm{u}}}}}{{1 + \frac{{{T_{\rm{d}}}}}{{{T_{\rm{u}}}}}}}$。结合引理2和引理3，得到定理2。

令定理2中K=3，得到以下结果。

推论3   对于L=2，K=3的M×NMIMO mRC，当考虑完整数据交换模型，并且考虑半双工通信时，优化上行/下行链路的时隙分配为

$ \frac{{{T_{\rm{u}}}}}{{{T_{\rm{d}}}}} = \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {\frac{1}{2}, \;\:{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{M}{N} \in \left( {0, \frac{1}{5}} \right]}\\ {\frac{{5M}}{{2N}}, \;\:\frac{M}{N} \in \left( {\frac{1}{5}, \frac{1}{4}} \right]}\\ {\frac{5}{8}, \;\:{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{M}{N} \in \left( {\frac{1}{4}, \frac{5}{{12}}} \right]} \end{array}\\ \begin{array}{*{20}{l}} {\frac{{3M}}{{2N}}, \;{\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{M}{N} \in \left( {\frac{5}{{12}}, \frac{4}{9}} \right]}\\ {\frac{2}{3}, \;\:{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{M}{N} \in \left( {\frac{4}{9}, \frac{1}{2}} \right]}\\ {\frac{{4M}}{{3N}}, \;{\kern 1pt} \frac{M}{N} \in \left( {\frac{1}{2}, \frac{3}{5}} \right]} \end{array}\\ \begin{array}{*{20}{l}} {\frac{4}{5}, \;\:{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{M}{N} \in \left( {\frac{3}{5}, \frac{2}{3}} \right]}\\ {\frac{{6M}}{{5N}}, \;{\kern 1pt} {\kern 1pt} \frac{M}{N} \in \left( {\frac{2}{3}, \frac{5}{6}} \right]}\\ {1, \;\:{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{M}{N} \in \left( {\frac{5}{6}, 1} \right]} \end{array} \end{array} \right., $

(27a)

此时每个用户可达的一个DoF为

$ {d_{{\rm{user}}}}\left\{ \begin{array}{l} \begin{array}{*{20}{c}} {\frac{{2M}}{3}, }&{\frac{M}{N} \in \left( {0, \frac{1}{5}} \right]}\\ {{\rm{min}}\left\{ {\frac{{2N}}{{5 + \frac{{2N}}{M}}}, \frac{{2N}}{{13}}} \right\}, }&{\frac{M}{N} \in \left( {\frac{1}{5}, \frac{1}{3}} \right]}\\ {\frac{{6M}}{{13}}, }&{\frac{M}{N} \in \left( {\frac{1}{3}, \frac{5}{{12}}} \right]} \end{array}\\ \begin{array}{*{20}{c}} {{\rm{min}}\left\{ {\frac{N}{{2 + \frac{{4N}}{{3M}}}}, \frac{N}{5}} \right\}, }&{\frac{M}{N} \in \left( {\frac{5}{{12}}, \frac{1}{2}} \right]}\\ {{\rm{min}}\left\{ {\frac{N}{{2 + \frac{{3N}}{{2M}}}}, \frac{{2N}}{9}} \right\}, }&{\frac{M}{N} \in \left( {\frac{1}{2}, \frac{2}{3}} \right]}\\ {{\rm{min}}\left\{ {\frac{N}{{2 + \frac{{5N}}{{3M}}}}, \frac{N}{4}} \right\}, }&{\frac{M}{N} \in \left( {\frac{2}{3}, 1} \right]} \end{array} \end{array} \right.. $

(27b)

证明   当K=3时，上行链路存在以下候选角点(M/N, d_u)：

(U1) $\left( {\frac{1}{5}, \frac{N}{5}} \right)$；(U2) $\left( {\frac{5}{{12}}, \frac{N}{4}} \right)$。因此上行链路每个用户可达的DoF为

$ {d_{\rm{u}}} = \left\{ {\begin{array}{*{20}{l}} {{\rm{min}}\left\{ {M, \frac{N}{5}} \right\}, }&{\frac{M}{N} \le \frac{1}{3}}\\ {{\rm{min}}\left\{ {\frac{{3M}}{5}, \frac{N}{4}} \right\}, }&{\frac{1}{3} < \frac{M}{N} < 1} \end{array}} \right.. $

(28)

结合推论1下行链路可达的DoF以及定理2, 得到推论3。证毕。

注意：根据2.1节的讨论，当上行链路设计信号对齐满足rank(P_jM_j)≥(K－1)d_uT_u。下行链路采用文献[12]的结果，通过优化上行和下行链路的时隙分配，可以得到L≥2个用户集群，每个用户集群中K≥3个用户的MIMO mRC模型在半双工通信下可达的一个DoF。但是由于文献[12]中下行链路设计信号对齐的方式并不是最优的，所以最终得到的半双工通信下的结果并非最优。

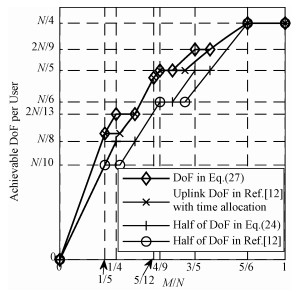
图 4给出半双工通信下L=2, K=3模型可达到的DoF。对于半双工通信，当不考虑上行和下行链路时隙优化分配时，系统可达的DoF是全双工通信的一半，很容易得到半双工通信下两个可达的DoF，即定理1中d_user的1/2以及文献[12]结果的1/2。在图 4中将此不考虑时隙分配的结果加入进行比较。同时，如前所述，结合2.1节的讨论，文献[12]的结果经过上行和下行时隙优化分配，很容易推广到半双工通信。对于L=2, K=3，当上行链路设计信号对齐得到式(28)，下行链路采用文献[12]中的信号对齐方式时，可以推出半双工通信下经过上行/下行时隙优化后一个可达的DoF。将此结果加入图 4进行比较。结果发现当M/N < 5/6时，进行时隙优化分配后的结果明显优于不进行时隙分配的结果。同时，由于下行链路考虑了2个更优的角点(1/4，N/4)和(3/5，2N/5)，在这2个角点附近可得到更优化的DoF。

注意：半双工通信时，上行和下行链路信号对齐非对称设计使得系统DoF进一步提高。这是因为对于一次完整的数据交换，上行链路中继端需要解出一个集群所有用户发送的信号，对应于式(13a)，下行链路中继端为每个集群中的所有用户发送相同的信号，对应于式(13b)。很明显，上行链路的信号对齐要求相比下行链路降低了，这是因为如果上行链路一个集群的信息在中继端压缩得过于严重时，需要消耗多余的时隙将压缩的信息解出来。

5 总结

由于L个用户集群，每个集群K个用户的MIMO mRC的完整数据交换模型较为复杂，目前此模型全双工通信和半双工通信下的信道容量是未知的。本文主要对两个集群，每个集群K个用户的MIMO mRC的完整数据交换模型进行分析。由于数据交换模型的特殊性，上行和下行链路的信号对齐是不对称的，所以对上行链路和下行链路分别设计信号对齐，得到相应的角点，并根据角点给出每个用户上行链路可以发送的独立数据流数目d_u和下行链路可以接收的独立数据流数目d_d。对于全双工通信，假设每个结点可以进行自干扰消除，通过令T_u=T_d=T，推出此模型在全双工通信下的结果。同时，由于下行链路是网络的瓶颈，通过上行和下行链路非对称设计，并且优化上行/下行链路时隙分配，得到半双工通信下一个优化的DoF。

通过给出全双工通信下L=2, K=3和L=2, K=4的可达DoF，验证了我们的结果优于目前已知的结果^[12]，并和通过算法优化得到的结果^[14]相同。同时通过优化上行/下行链路时隙分配T_u/T_d，半双工通信下的L=2, K=3系统的DoF进一步得到提高。本文分析对于更一般的完整数据交换模型(L>2)在全双工通信和半双工通信下的DoF分析有参考价值。