2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
物联网和移动互联网的快速发展给第五代(5G)移动通信研究提出了诸多挑战,比如更低的系统时延、更高的吞吐量、超大规模的连接和更好的服务质量[1]。稀疏码分多址(sparse code multiple access,SCMA)作为频率域的非正交多址技术[2-3],综合LDS技术的稀疏性和QAM调制的高效性,可以适应大规模连接、低时延和高吞吐量的通信场景,成为5G非正交多址技术中有竞争力的候选方案。
SCMA的核心思想是利用多维稀疏码本将信息流直接映射成复数域数据流,利用码本的非正交性,用户的信息将稀疏地分散在不同的子载波上。接收端使用基于因子图迭代的消息传递算法(message passing algorithm,MPA)[4]解码作为次优解码方案,其本质是基于置信度传播(belief propagation,BP)算法[5]的演进,相比最优性能的最大后验概率算法(maximum a posteriori probability,MAP)和极大似然算法(maximum likelihood algorithm,ML),MPA算法计算复杂度更低。
原始MPA在因子图中沿着边缘传递所有节点的消息,直至达到最大迭代次数,但是当系统严重超载以及用户过多时复杂度会剧增。文献[6]提出将乘法与指数运算转化为加法与求极值运算的对数域max log-MPA算法方案,从运算角度简化复杂度,文献[7-8]研究FPGA上的MPA和log-MPA的定点和浮点实现,改进log-MPA算法方案,使其可以在性能和复杂性之间实现良好的权衡。基于部分边缘更新(partial marginalizition-based MPA,PM-based MPA)方案[9]、用剪枝的思想暂停部分节点更新,从降低搜索路径长度角度降低计算复杂度。文献[10]根据信息论的定义,引入动态自适应边缘选择MPA(edge selected MPA,ES-MPA)方案,由每条边迭代更新产生的信息量决定是否进行下一轮FN节点到VN节点的更新,能够在BER和复杂度间取得良好平衡。SCMA接收端使用消息传递算法及优化译码方案,能有效降低译码复杂度,但在高SNR情境下,误比特率性能未成瀑布状分布。
为进一步提升高SNR场景下BER性能,降低高SNR的需求,本文在优化SCMA译码效率的前提下,在SCMA调制编码前级联部分响应信号模块,提出部分响应与稀疏多址联合调制模型。在不损失频带利用率的前提下,依然能够消除码间干扰(ISI),提出MPA-Viterbi联合译码算法(MPA-VA),能够有效降低SNR的需求,取得较低的误比特率。在部分响应系统译码算法方面,引入基于极大似然算法的Viterbi译码算法[11],利用相关编码特性在误比特率方面的优势,并且在Viterbi译码器之前加入白化匹配滤波器,有效提升Viterbi算法非线性递归运算的先验值。
1 联合编码模型虽然SCMA模块具有高过载率,但在高SNR环境中,误比特率不能显著下降。同时,部分响应是一种卷积编码[12],具有卷积编码的特性,可以提高符号之间的容错性部分。部分响应和稀疏码分多址联合调制解码模型继承了SCMA的高过载率和部分响应的高容错性,在大规模连接的情况下可以保持低误比特率,特别是在高信噪比情况中,联合调制模型BER性能有明显优势。
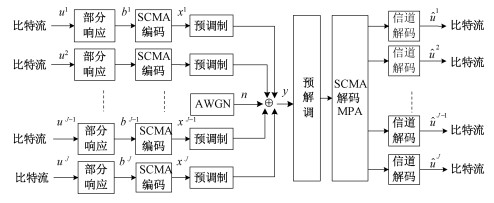
本方案在编码侧使用部分响应与稀疏码分多址联合调制,J个用户使用K资源块的SCMA下行传输流程如图 1所示,第j个用户发送的信息序列uj首先经过部分响应模型,人为引入可控制的码间串扰,经过SCMA编码、调制过程,进入高斯信道发送到接收机端,接收机端通过MPA-VA联合译码算法获得估计序列
|
Download:
|
| 图 1 J个用户K个资源块的SCMA简化下行链路图 Fig. 1 Simplified downlink diagram of SCMA with J users and K resource blocks | |
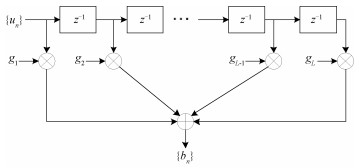
假设在理想信道的情况下,一个用户的输入比特流序列表示为u=[u1, u2, …, un],经过部分响应模型,如图 2所示,在每个比特间引入的冗余码字[12]为
| $ {b_n} = \sum\limits_{l = 1}^L {{u_{n - (l - 1)}}} {g_l}, $ | (1) |
|
Download:
|
| 图 2 部分响应的离散模型 Fig. 2 Discrete model of partial response | |
式中:un为二进制比特数据;这里的{gl},l∈[1, 2, …, L],表示L个采样点的抽头系数。那么u经过部分响应实际上可看作一种编码效率为1/2的编码。
目前部分响应信号解码主要有两种概率译码方案:1)基于极大似然的检测方案(Viterbi);2)基于最大欧氏距离的最大似然序列检测(MLSE)[13]。
根据部分响应信道的码间串扰特性,可以看作单入单出的卷积码,因此可以使用成熟的BCJR或Viterbi译码算法来降低译码复杂度。本文使用Viterbi算法的考量在于,算法的最大似然译码特性,能够获得最小误比特率,且接近MLSE。
1.2 SCMA模型在SCMA模型中,J个用户共用K个资源块来传输数据。所有的用户经过部分响应模型的比特流为B=[b1, b2, …, bj],其中bj=[b1j, b2j, …, bnj],j∈[1, J],表示第j个用户经过部分响应的比特流。比特流B进入SCMA编码器,根据码本进行映射fj:bj→xj,得到X=[x1, x2, …, xj],其中xj=[x1j, x2j, …,xKj]T,xKj表示第j个用户发送到第k个资源块上的符号。
本文取J=6,K=4,则6个用户共用4个资源块方式用矩阵表示为
| $ \mathit{\boldsymbol{F}} = \left[ {\begin{array}{*{20}{l}} 0&1&1&0&1&0\\ 1&0&1&0&0&1\\ 0&1&0&1&0&1\\ 1&0&0&1&1&0 \end{array}} \right]. $ | (2) |
这里Fkj=1表示用户j占用资源块k;Fkj=0,表示用户j不占用资源块k,对应的因子图如图 3所示。

|
Download:
|
| 图 3 J=6, K=4的因子图 Fig. 3 Factor graph for J=6 and K=4 | |
各个用户发送的数据在每个资源块上进行叠加,经过高斯信道,在接收机端,接收信号可表示为
| $ \mathit{\boldsymbol{y}} = \sum\limits_{j = 1}^J {{\mathop{\rm diag}\nolimits} } \left( {{\mathit{\boldsymbol{h}}_j}} \right){\mathit{\boldsymbol{x}}^j} + \mathit{\boldsymbol{n,}} $ | (3) |
式中:y=(y1, y2, …, yK)T表示接收信号矢量,yK表示第k个资源块上接收的符号;hj=(h1, j, h2, j, …, hK, j)T表示信道增益矢量,hK, j表示第j个用户到第k个资源块上的信道增益因子;xj=(x1j, x2j, …, xKj)T表示用户j发送的码字,xKj表示第j个用户发送到第k个资源块上的符号,n=[n1, n2, …,nK]T,表示高斯白噪声矢量。
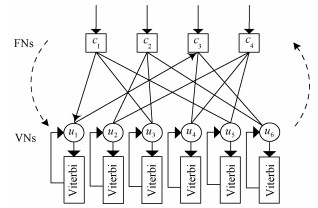
2 联合检测译码模型通过AWGN的接收信号,接收数据序列使用基于MPA和Viterbi的联合迭代解调模块,判决并输出估计序列。其中,MPA解码的核心单元是VNs与FNs之间的迭代更新,而这个迭代过程可以分两个步骤进行,本文联合译码算法在迭代更新过程中加入Viterbi译码算法。具体联合译码流程如图 4所示。
|
Download:
|
| 图 4 SCMA-PR联合因子图 Fig. 4 SCMA-PR joint factor graph | |
第1步:信号初始化。通过使用期望值和接收值的欧氏距离,从计算接收到的每个资源所有组合的附加码字的概率开始。由于缺少码字的先验信息,所以假设资源节点FNs在每个用户节点VNs取得每个符号的概率是相等的,即初始化时,第j个用户节点向第k资源节点的转移概率为
| $ \mathit{\boldsymbol{I}}_{j \to k}^{{\rm{init}}}(\mathit{\boldsymbol{x}}_m^j) = \frac{1}{M}, m = 1, \cdots , M, $ | (4) |
式中:M表示进制数,xmj表示xj的第m个符号值。
接收机基于设定好的用户码本,计算每个资源节点FN上接收的不同比特信息的概率为
| $ \begin{array}{l} {P_{k, j}}\left( {\mathit{\boldsymbol{x}}_m^j} \right) = \frac{1}{{\sqrt {2{\rm{ \mathit{ π} }}} \sigma }}\exp \left( { - \frac{1}{{2{\sigma ^2}}}} \right.\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\parallel {y_k} - \sum\limits_{} {_{i \in {\xi _k}}{h_{k, i}}} {x_{k, i, m}}{\rm{ }}\left. {{\parallel ^2}} \right), \end{array} $ | (5) |
式中:PK, j(xmj)是第j个用户节点VN到第k个资源节点FN的置信概率,yK表示第k个资源节点FN上接收的符号信息,ξK表示第k个资源节点FN连接的用户节点VN的个数。
第2步:资源节点FN更新。将资源节点FN收到的先验概率信息式(5)与当前概率计算结果相结合,进行节点更新,
| $ I_{k \to j}^t\left( {\mathit{\boldsymbol{x}}_m^j} \right) = \sum\limits_{} {_{\mathit{\boldsymbol{\tilde x}}_m^j}{P_{k, j}}} \left( {\mathit{\boldsymbol{x}}_m^j} \right)\prod\limits_{} {_{j \in {\xi _{k/j}}}I_{j \to k}^{l - 1}} \left( {\mathit{\boldsymbol{x}}_m^j} \right), $ | (6) |
式中:Ik→jt(xmj)表示第t次迭代过程中,资源节点k到用户节点j的更新信息;j∈ξk/j,表示除去用户节点j的ξK。然后计算符号的外部信息为
| $ {P_{k, j}}\left( {\mathit{\boldsymbol{x}}_m^j} \right) = \prod\limits_{} {_{k \in {\xi _j}}I_{k \to j}^t} \left( {\mathit{\boldsymbol{x}}_m^j} \right), $ | (7) |
式中:ξj表示第j个用户节点VN连接的资源节点FN的个数。
第3步:Viterbi译码更新符号信息。Viterbi译码器接收的信号为式(7),按Viterbi算法流程进行译码,符号的外部信息更新为
| $ P\left( {\mathit{\boldsymbol{x}}_m^j} \right) = {\rm{Viterbi(}}{P_k}\left( {\mathit{\boldsymbol{x}}_m^j} \right){\rm{)}}{\rm{.}} $ | (8) |
第4步:用户节点VN更新。用户节点VN接收的信息结合第3步更新的符号信息,进行和积操作,并对VN节点进行归一化操作,
| $ I_{j \to k}^t\left( {\mathit{\boldsymbol{x}}_m^j} \right) = {\rm{normalize(}}P\left( {\mathit{\boldsymbol{x}}_{jm}^{}} \right)\prod\limits_{} {_{\tilde k \in {\xi _j}/k}I_{k \to j}^{l - 1}} \left( {\mathit{\boldsymbol{x}}_m^j} \right){\rm{)}}, $ | (9) |
第5步:估计与软输出。在式(6)~式(9)之间进行tmax次迭代后,最终第j个VN节点经过估计后的LLR软输出为
| $ {{\hat X}_j}\left( {\mathit{\boldsymbol{x}}_m^j} \right) = \prod\limits_{} {_{k \in {\xi _j}}I_{k \to j}^{{t_{\max }}}} \left( {\mathit{\boldsymbol{x}}_m^j} \right). $ | (10) |
为表述清晰,具体VA-MPA运算伪代码流程,如下所示:
|
|
本文基于下行SCMA通信系统,采用文献[8]中给出的码本矩阵,仿真分析SCMA-PR联合调制译码设计方案在高斯信道中的BER性能。基于文献[4-10]中提出的标准MPA、PM-MPA和ES-MPA3种MPA算法,在前置部分响应模块后,使用联合译码模块进行解调。方案适当增加复杂度,提高在高信噪比下的BER性能。因此将在不同的信噪比下,分别对比MPA和VA-MPA、PM-MPA和VA-PM-MPA、ES-MPA和VA-ES-MPA的BER性能,从而验证本方案的性能。VA-PM-MPA表示级联Viterbi译码的PM-MPA译码算法,VA-ES-MPA同理。同时,将本文联合调制译码方案与文献[14-17]提出的Polar级联SCMA译码方案(BP-MPA)进行BER性能对比。仿真关键参数如表 1所示。
|
|
表 1 部分响应与稀疏多址译码仿真参数 Table 1 Partial response and sparse multiple access decoding simulation parameters |
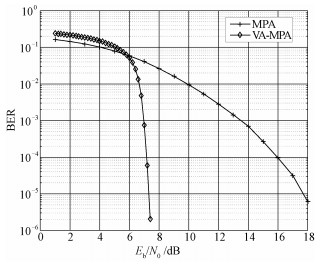
MPA与VA-MPA响应联合译码方案性能对比如图 5所示。从图中可看出:Eb/N0在1~5 dB范围时,由于部分响应模块需要根据输入数据添加冗余比特,使得进入SCMA映射矩阵的比特数增加1倍,因此在低信噪比场景下VA-MPA的误比特率性能与MPA相比衰减约1 dB;在Eb/N0>6 dB时,VA-MPA与MPA译码方案相比优势明显;当Eb/N0在6~8 dB范围时,BER迅速从10-2降到10-6量级。当BER=10-5时,本文方案较标准MPA方案的信噪比可改善10.4 dB。
|
Download:
|
| 图 5 MPA与VA-MPA译码误比特率对比图 Fig. 5 Comparison of BER performance between MPA and VA-MPA decoding algorithms | |
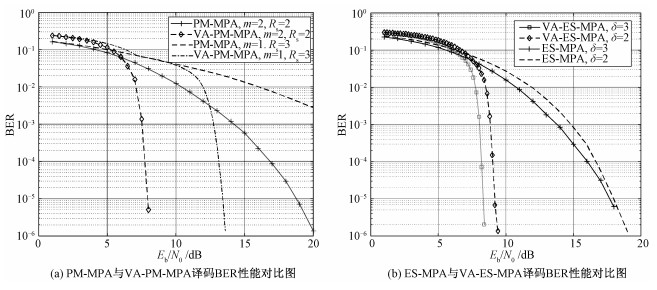
PM-MPA与VA-PM-MPA联合译码方案BER性能对比如图 6(a)所示。根据PM-MPA算法的特点,取两组m、Rs值进行对比,分别为m=1、Rs=3和m=2、Rs=2。由图中可知,在高信噪比场景下,VA-PM-MPA译码方案在误比特率方面始终优于PM-MPA。以m=1、Rs=3对比曲线为例,在信噪比2~11 dB, PM-MPA的BER性能逼近VA-PM-MPA方案,VA-PM-MPA方案优势不突出。对于m=2, Rs=2,在Eb/N0>6 dB时,VA-PM-MPA译码方案与PM-MPA方案相比优势明显,随后Eb/N0在6~8 dB范围内,BER迅速从10-2降到10-5量级。当BER=10-5时,VA-PM-MPA方案较PM-MPA方案的信噪比可改善将近11 dB。
|
Download:
|
| 图 6 不同算法的误比特率性能对比图 Fig. 6 Comparison of BER performance among different algorithms | |
ES-MPA与VA-ES-MPA联合译码方案BER性能对比如图 6(b)所示。此处ES-MPA与VA-ES-MPA的仿真参数采用两组阈值进行对比,分别为δ=2、δ=3。对比两组曲线,在高信噪情况下,VA-ES-MPA方案的BER性能优势明显。以δ=3对比曲线为例, 当Eb/N0>7 dB时,VA-ES-MPA相较于ES-MPA方案的BER值骤减且呈瀑布状,表明部分响应在高信噪比场景下优势明显。当BER=10-5时,VA-ES-MPA方案较ES-MPA方案信噪比提高9 dB。对比两条VA-ES-MPA方案曲线,当BER=10-5时,两组参数曲线的信噪比仅相差1.2 dB。
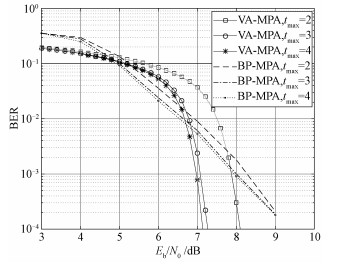
VA-MPA联合译码方案与BP-MPA联合译码方案性能对比如图 7所示,此处分别对两种方案迭代2、3、4次。对比两组曲线,在高信噪比的情况下,VA-MPA方案的BER性能优势明显。以迭代次数tmax=4为例,当Eb/N0>6 dB时,VA-MPA相比较于Polar级联联合译码方案的BER值骤减且呈瀑布状,表明部分响应在高信噪比场景下优势明显; 当BER=10-4时,VA-MPA方案较BP-MPA方案的信噪比可改善大约2 dB。
|
Download:
|
| 图 7 VA-MPA与BP-MPA译码误比特率对比图 Fig. 7 Comparison of BER performance between VA-MPA and BP-MPA decoding algorithms | |
本文综合部分响应的容错率和SCMA系统的稀疏性,提出部分响应与稀疏码分多址联合调制解码模型。在SCMA调制编码前级联部分响应模块,即使用部分响应的卷积特性将输入信号进行预编码。在接收侧,综合基于MLSE的Viterbi译码算法和MPA算法,给出新型MPA-VA联合译码方案。仿真结果表明,标准MPA、PM-MPA和ES-MPA3种SCMA译码方案,在联合VA译码后,BER性能曲线在高Eb/N0情境下,呈瀑布状分布,并且优于Polar级联SCMA译码方案。表明,本文提出的联合编译码模型能够有效增加高Eb/N0情况下的BER性能界。由于引入卷积编码,使系统整体计算复杂度有一定升高,因此在未来工作中,深入研究降低系统的计算复杂度是有必要的。
| [1] |
Dai L, Wang B, Yuan Y, et al. Non-orthogonal multiple access for 5G:solutions, challenges, opportunities, and future research trends[J]. IEEE Communications Magazine, 2015, 53(9): 74-81. |
| [2] |
Ma Z, Zhang Z Q, Ding Z G, et al. Key techniques for 5G wireless communications:network architecture, physical layer, and MAC layer perspectives[J]. Science China:Information Sciences, 2015, 58(4): 1-20. |
| [3] |
Benjebbour A, Saito Y, Kishiyama Y, et al. Concept and practical considerations of non-orthogonal multiple access (NOMA) for future radio access[C]//2013 International Symposium on Intelligent Signal Processing and Communication Systems. IEEE, 2013: 770-774.
|
| [4] |
Nikopour H, Baligh H. Sparse code multiple access[C]//2013 IEEE 24th Annual International Symposium on Personal, Indoor, and Mobile Radio Communications (PIMRC). IEEE, 2013: 332-336.
|
| [5] |
Kihara K, Nishimura T, Ohgane T, et al. Signal detection with belief propagation in faster-than-Nyquist signaling[C]//2017 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC). IEEE, 2017: 1790-1794.
|
| [6] |
Zhang S, Xu X, Lu L, et al. Sparse code multiple access: an energy efficient uplink approach for 5G wireless systems[C]//2014 IEEE Global Communications Conference. IEEE, 2014: 4782-4787.
|
| [7] |
Ghaffari A, Leonardon M, Cassagne A, et al. Toward high-performance implementation of 5G SCMA algorithms[J]. IEEE Access, 2019, 7: 10402-10414. |
| [8] |
Liu J, Wu G, Li S, et al. On fixed-point implementation of Log-MPA for SCMA signals[J]. IEEE Wireless Communications Letters, 2016, 5(3): 324-327. |
| [9] |
Mu H, Ma Z, Alhaji M, et al. A fixed low complexity message pass algorithm detector for up-link SCMA system[J]. IEEE Wireless Communications Letters, 2015, 4(6): 585-588. |
| [10] |
Wang Y, Qiu L. Edge selection-based low complexity detection scheme for SCMA system[C]//2016 IEEE 84th Vehicular Technology Conference (VTC-Fall). IEEE, 2016: 1-5.
|
| [11] |
Forney G. Maximum-likelihood sequence estimation of digital sequences in the presence of intersymbol interference[J]. IEEE Transactions on Information theory, 1972, 18(3): 363-378. |
| [12] |
Rusek F. Partial response and faster-than-Nyquist signaling[D]. Lund: Lund University, 2007.
|
| [13] |
Taherzadeh M, Nikopour H, Bayesteh A, et al. SCMA codebook design[C]//2014 IEEE 80th Vehicular Technology Conference (VTC2014-Fall). IEEE, 2014: 1-5.
|
| [14] |
Pan Z, Li E, Wen L, et al. Joint iterative detection and decoding receiver for polar coded SCMA system[C]//2018 IEEE International Conference on Communications Workshops (ICC Workshops). IEEE, 2018: 1-6.
|
| [15] |
张弩天.极化码的译码算法研究及其应用[D].成都: 电子科技大学, 2018.
|
| [16] |
符杰林, 张剑波, 王俊义. SCMA与极化码的联合检测译码技术[J]. 计算机应用研究, 2019(9): 1-6. |
| [17] |
Pan Z, Li E, Zhang L, et al. Design and optimization of joint iterative detection and decoding receiver for uplink polar coded SCMA system[J]. IEEE Access, 2018, 6: 52014-52026. |
 2020, Vol. 37
2020, Vol. 37 


