辉石(pyroxene)主要存在于地壳与上地幔中,是大部分镁铁质到超镁铁质火成岩和高级变质岩中的重要组成矿物,同时也是上地幔中除橄榄石以外含量最多的矿物[1-3]。因此,对辉石物性的研究有助于更好地理解地球深部的物质组成和地震波速异常及动力学过程等。
目前,国际上对地球深部矿物物性的研究主要有两种方式:一种是高温高压实验,就是利用各种静态超高压实验设备,包括大腔体高压装置和金刚石压腔装置,并与超声、X射线衍射、红外和拉曼等多种谱学测量方法相结合,进行矿物物性原位测试[2, 4-6];另一种就是理论计算,主要是基于第一性原理(first principle)、分子动力学(molecular dynamics)和密度泛函理论(density functional theory)等,对矿物在温压下的物性进行模拟研究[3]。实验不可能完成所有材料在任意温压范围的物性测试,而理论计算可以弥补这个不足。理论计算能够提供从微观到宏观多尺度时空范围内的研究手段,是很多地球科学分支之间的纽带和桥梁[7]。随着计算机软硬件的不断发展,理论计算在矿物物性研究中的作用越来越大,越来越多的研究者开始从事矿物物理计算研究。
辉石是上地幔中含量第二的矿物,前人的研究显示辉石的高压结构非常复杂,其中斜方辉石在高压下可能存在Pbca、P21/c、C2/c和P21ca等4种结构相[8-18]。但前人的研究多注重于晶体结构和相变,缺少对每种结构相的弹性波速的理论研究。高温高压实验对辉石弹性波速的研究主要有Kung等[9]利用超声波速测量并结合X射线衍射实验发现,斜方辉石多晶样品在9~13/14 GPa出现速度软化,这可能意味着样品发生了Pbca→ C2/c的相变;Li等[16]利用大腔体高压装置结合X射线衍射研究斜方铁辉石的纵横波速度,发现与镁辉石不同;Li和Neuville[19]用超声波干涉和XRD相结合的方法测量透辉石沿1 600 K绝热地温线的弹性波速和密度,表明在上地幔深度,透辉石的波速比斜方辉石大1%~3%。而辉石波速各向异性的研究,目前被广泛引用的数据是Anderson[1]报道的常温常压下斜方辉石沿3个结晶轴方向的纵波速度。而高压或高温下的辉石单晶体不同方向的速度资料非常匮乏。因为天然产出的斜方辉石以镁辉石为主,所以本研究选择镁辉石为研究对象,利用第一性原理对其在高压下4种结构相的弹性波速进行理论计算。
1 镁辉石的结构特征辉石属于单链硅酸盐矿物,根据晶体对称性的不同,辉石分为斜方辉石(orthopyroxene,Opx)和单斜辉石(clinopyroxene,Cpx)两个亚族,前者空间群为Pbca,后者为C2/c或P21/c[20-21]。
辉石主要由共角的TO4四面体和共边的MO6八面体沿着[100]方向交互成层排列而成。辉石的化学式一般可写作M2M1T2O6,其中M位一般被Mg、Fe、Al、Ca、Na等金属阳离子占据,M1通常为6配位八面体,M2为6~8配位的畸变的八面体,当M2被较小阳离子占据,辉石就是斜方晶系,而如果M2被较大阳离子占据,M2八面体就会比M1八面体略大,形成单斜晶系。O位根据成键特征可分为电价平衡的O1、未充分成键的O2,及充分成键的O3(又称为桥氧)。常温常压下镁辉石为斜方晶系,化学式可以简写为Mg2Si2O6,基本结构单元是SiO4单链,链与链之间的八面体空隙由Mg2+占据,所以镁辉石的结构为MgO6八面体和SiO4四面体交互成层沿a轴方向排列(图 1)。

|
Download:
|
| SiO4四面体为蓝色,白色为另一层的SiO4四面体,MgO6八面体为黄色。 图 1 镁辉石在[100]方向的投影 Fig. 1 Projection of Mg-pyroxene onto the [100] direction | |
计算是利用Quantum Espresso软件包[22]实现的,运用基于密度泛函理论的第一性原理进行计算,使用局域密度近似[23-24]作为交换关联函数。离子势能的近似基于平面波赝势理论,其中镁元素的赝势采用Von Barth-Car方法产生的模守恒赝势,硅和氧元素的赝势采用Vanderbilt方法产生的超软赝势[25]。赝势近似的价电子结构分别是3s23p2(Si)、3s2(Mg)和2s22p4(O)。
2.1 计算参数选择斜方结构的镁辉石Pbca和P21ca的晶胞都含有80个原子,经过能量收敛测试之后,最终选定平面波截断能为70 Ry,电子密度截断能为平面波截断能的4倍,即280 Ry;第一布里渊区k点取1×2×4[26]。
单斜结构的镁辉石P21/c和C2/c的晶胞里有40个原子,平面波截断能设为80 Ry,电子密度截断能也是平面波截断能的4倍,为320 Ry;k点取为4×4×4。
截断能和布里渊区采样网格点的选定,能够保证每一次晶胞结构优化之后,原子的能量收敛标准在2.0×10-5 Ry/atom,电子能量收敛标准在1.0×10-8 Ry,原子受力不超过2.0×10-4 Ry/bohr。为保证结果的可靠性,实际计算时先选定Pbca相的几个压力点进行测试,并与Kung等[9]给出的实验数据进行对照,验证计算数据的合理性及一致性后,完成4种结构不同压力下的弹性计算。这样处理后选定的参数,能够保证弹性计算的可靠性[3]。
2.2 弹性系数的计算镁辉石的初始晶胞结构模型选择Molin[27]及Thompson和Downs[28]的数据。利用Quantumn Espresso软件包中的PWscf模块对每个结构进行给定压力下的结构优化,得到该压力下的晶胞参数。总共对4种结构相在0~30 GPa压力范围各自9个压力点进行结构优化,并得到相应压力下的晶胞参数。
弹性系数cij利用应变-应力的关系得到,即通过对平衡结构的晶胞施加一个±1%的应变,然后固定晶胞体积,只优化原子位置,得到一个应力矩阵之后,通过胡克定律得到弹性系数。考虑辉石结构的空间对称性后,斜方结构的镁辉石含有9个弹性系数,分别为c11、c22、c33、c44、c55、c66、c12、c13和c23;而单斜结构的镁辉石含有13个弹性系数(另外4个分别为c15、c25、c35和c46)。
2.3 弹性波速及其各向异性的计算得到不同压力下的弹性系数后,利用弹性系数cijkl和Christoffel方程[29]可以得到沿着不同方向传播的弹性波速度:
| $ \left| {{c_{ijkl}}{n_j}{n_l} - \rho {V^2}{\delta _{ik}}} \right| = 0. $ |
式中:n为波的传播方向,δik为Kroncker函数,ρ为密度,V为波速。求解上面的方程可得到3个解,分别代表纵波速度和两个横波速度(快波和慢波)。
因为辉石不仅在上地幔中含量丰富,而且各向异性也很强,因此特别计算了镁辉石的波速各向异性。
得到纵波速度后,利用下式可以得到纵波的速度各向异性:
| $ {A_p} = 300\% \left( {{V_{{P_{\max }}}} - {V_{{P_{\min }}}}} \right)/\left( {{V_{P(a)}} + {V_{P(b)}} + {V_{P(c)}}} \right), $ |
式中:VP(a)、VP(b)和VP(c)分别代表沿3个晶体轴方向传播的纵波速度,VPmax和VPmin分别是3个值中的最大值和最小值。
而横波的速度各向异性可通过下式获得:
| $ {A_S} = 200\% \left( {{V_{S1}} - {V_{S2}}} \right)/\left( {{V_{S1}} + {V_{S2}}} \right), $ |
式中:VS1和VS2分别代表横波快波和慢波速度。
3 计算结果对于镁辉石4种结构相在高压下的稳定性和相变问题,我们已经在之前的文章中报道过[3],这里只讨论它们的弹性波速计算结果。
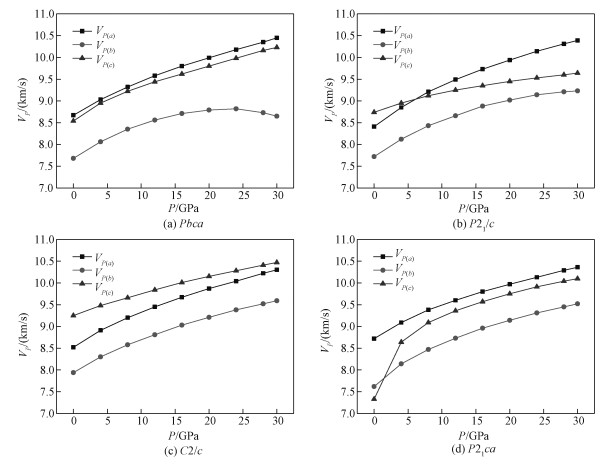
镁辉石4种结构相的轴向纵波速度随压力的变化如图 2所示:整体上,镁辉石的轴向纵波速度是随着压力的增加而增大,但是当压力大于24 GPa时,Pbca的b轴方向的纵波速度与压力呈负相关,即呈现出速度弱化趋势。4种结构中,除C2/c和个别低压点外,其余3种基本上都是VP(a)>VP(c)>VP(b),只有C2/c为VP(c)>VP(a)>VP(b)。
|
Download:
|
| 图 2 不同压力下镁辉石4种结构相的轴向纵波速度 Fig. 2 Axial compressional wave velocities of the four structural phases of Mg-pyroxene as a function of pressure | |
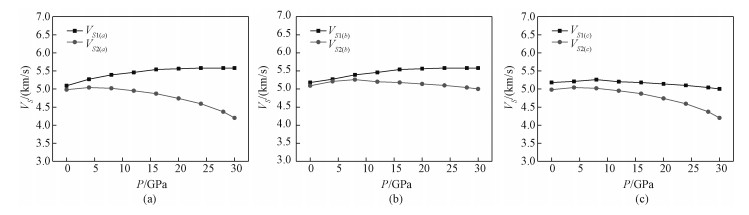
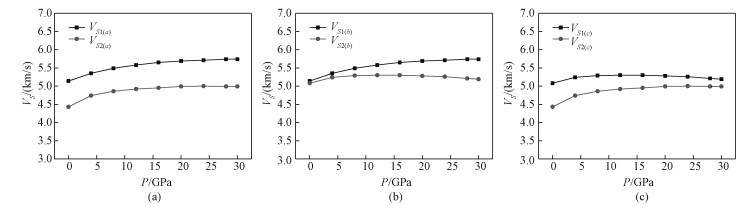
图 3~图 6分别为4种结构相的轴向横波速度随压力的变化。结果显示,Pbca和P21/c的3个结晶轴方向快波和慢波的速度差都随压力升高逐渐最大;而C2/c和P21ca的横波速度变化比较复杂:随压力升高,有些方向速度差变化不大(如a轴方向),有些逐渐增大(如P21ca的b轴方向),有些逐渐减小(如C2/c的b轴方向和P21ca的c轴方向),而个别是先减小后增大(如C2/c的c轴方向)。
|
Download:
|
| 图 3 不同压力下镁辉石Pbca相的轴向横波速度 Fig. 3 Axial shear wave velocity of the Pbca phase of Mg-pyroxene as a function of pressure | |

|
Download:
|
| 图 4 不同压力下镁辉石P21/c相的轴向横波速度 Fig. 4 Axial shear wave velocity of the P21/c phase of Mg-pyroxene as a function of pressure | |

|
Download:
|
| 图 5 不同压力下镁辉石C2/c相的轴向横波速度 Fig. 5 Axial shear wave velocity of the C2/c phase of Mg-pyroxene as a function of pressure | |
|
Download:
|
| 图 6 不同压力下镁辉石P21ca相的轴向横波速度 Fig. 6 Axial shear wave velocity of the P21ca phase of Mg-pyroxene as a function of pressure | |
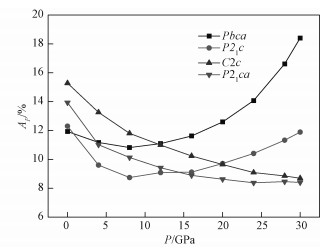
镁辉石4种结构相的纵波速度各向异性如图 7所示,在压力约低于12 GPa时,C2/c的各向异性最大;在更高的压力下时,Pbca的各向异性最强,且随着压力急剧上升,C2/c相的各向异性越来越弱;压力高于14 GPa后P21ca相的各向异性最小。
|
Download:
|
| 图 7 镁辉石4种结构相的纵波速度各向异性 Fig. 7 Compressional wave velocity anisotropy of the four structural phases of Mg-pyroxene | |
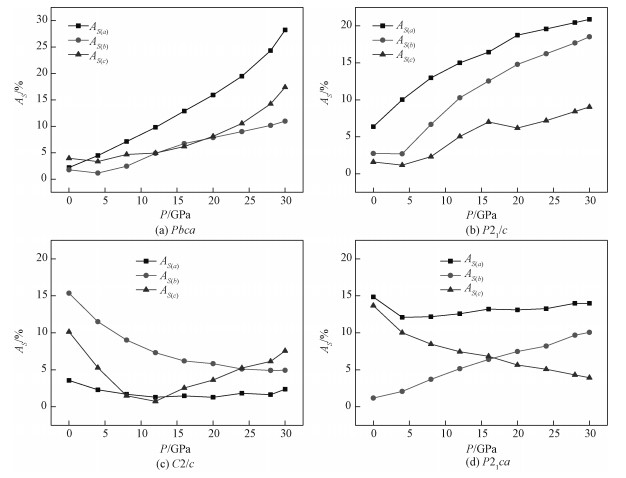
图 8为镁辉石4种结构相的轴向横波速度各向异性,可以看出:Pbca相,a轴横波速度各向异性最明显;3个方向的横波速度各向异性随着压力的增大而增大(P>4 GPa)。P21/c相,a轴横波速度各向异性最明显;3个方向的横波速度各向异性随着压力的增大而增大(c轴方向在16~20 GPa之间有一个减小,20 GPa之后继续单调递增)。C2/c相,压力小于24 GPa时b轴横波速度各向异性最明显,更高的压力下c轴横波速度各向异性最大;b轴方向的横波速度各向异性随着压力的增大而减小;c轴先减小,压力达到12 GPa后开始增大;a轴的变化不明显。P21ca相,a轴横波速度各向异性最大;随着压力的增大,a轴横波速度各向异性变化不明显;b轴横波速度各向异性随着压力的增大而增大,c轴横波速度各向异性随着压力的增大而减小,两者的交叉点在16 GPa附近,此压力点之前b轴各向异性最小,之后c轴各向异性最小。
|
Download:
|
| 图 8 镁辉石4种结构相的轴向横波速度各向异性 Fig. 8 Shear wave velocity anisotropy of the four structural phases of Mg-pyroxene | |
以上计算结果显示,不同结构相镁辉石的波速各向异性特征复杂且多变。在地幔条件下,根据Kung等[9]、Nestola等[11]、Jahn[13]、Zhang等[15]、Li等[16]、Finkelstein等[17]、Yu等[30]和Xu等[31]的最新研究结果,随着压力的增加,镁辉石很有可能相变为不同的高压相结构。这种相变完全可能引起镁辉石各向异性特征的改变,而以镁辉石为代表的斜方辉石是上地幔中的主要组成矿物,因此高压下镁辉石的相变引起的波速各向异性的变化非常可能造成上地幔中观测到的地震波速异常。反过来,根据4种结构相的波速计算结果,无论镁辉石在高压下相变为何种结构,其各向异性都有明显的差别,所以如果上地幔局部地区的各向异性是由镁辉石引起的,也可以通过将地震波观测到的各向异性与镁辉石的4种结构的各向异性特征进行对比分析,就可能判断出实际的镁辉石在上地幔中的真实相结构。最新的Zhang和Bass通过对天然含Fe的Pbca相单晶的实验研究,认为Pbca→P21/c的相变不可能是250~325 km深度X不连续面的成因,反而可能是上地幔更深处地震波各向异性的成因[32]。这体现了对镁辉石波速各向异性研究的意义。
镁辉石在高压下结构相变和不同结构相各向异性复杂的原因,本质是由其晶体结构导致的。由于镁辉石的结构为MgO6八面体和SiO4四面体交互成层沿a轴方向排列(图 1),所以在高压下a轴方向最抗压,波速较大;而b轴和c轴的分别与四面体、八面体链的滑移以及链的旋转、扭结有关,所以b轴方向容易变形,波速较小;c轴方向中等[3, 16, 18]。
5 结论与展望本文利用第一性原理对镁辉石高压下的4种结构相的弹性波速及其各向异性进行研究,发现:4种结构的镁辉石弹性波速度均表现出明显的各向异性;压力小于12 GPa时,高压单斜相C2/c的纵波波速各向异性最大,而在更高的压力下,Pbca的各向异性最大,且随着压力急剧上升;除C2/c结构外,其他结构相都是a轴方向的横波波速各向异性最明显。研究结果为上地幔的地震波速异常的解释提供了新的依据。
目前的计算只考虑压力,并未考虑温度的影响。而实际地幔中是高温高压环境,温度的加入将会使辉石的结构、弹性波速及其各向异性变得更为复杂。但是,仅仅压力的改变,就会引起辉石结构和弹性波速及其各向异性的明显变化,所以,未来对于辉石矿物物理的研究,不仅要继续关注其相变问题,更要重视其弹性各向异性及其相变前后的变化。
| [1] |
Anderson D L. New theory of the Earth[M]. Cambridge: Cambridge University Press, 2007.
|
| [2] |
徐志双, 马麦宁, 周晓亚. 金刚石压腔与地幔矿物物性研究[J]. 地球物理学进展, 2014, 29(1): 34-45. |
| [3] |
韩林, 马麦宁, 徐志双, 等. 辉石结构与相变的第一性原理研究[J]. 高压物理学报, 2017, 31(2): 125-134. |
| [4] |
王慧媛, 郑海飞. 高温高压实验及原位测量技术[J]. 地学前缘, 2009, 16(1): 17-26. |
| [5] |
刘川江, 郑海飞. 金刚石压腔(DAC)技术及其在地球科学中的应用[J]. 地学前缘, 2012, 19(4): 141-150. |
| [6] |
张艳飞, 吴耀, 刘鹏雷, 等. Walker型28GPa多面砧压机及其在地球科学中的应用[J]. 地球科学-中国地质大学学报, 2012, 37(5): 955-965. |
| [7] |
刘耘. 国内理论及计算地球化学十年进展[J]. 矿物岩石地球化学通报, 2013, 32(5): 531-543. |
| [8] |
Angel R J, Chopelas A, Ross N L. Stability of high-density clinoenstatite at upper-mantle pressure[J]. Nature, 1992, 358(6384): 322-324. Doi:10.1038/358322a0 |
| [9] |
Kung J, Li B, Uchida T, et al. In situ measurements of sound velocities and densities across the orthopyroxene→high-pressure clinopyroxene transition in MgSiO3 at high pressure[J]. Physics of the Earth and Planetary Interiors, 2004, 147: 27-44. Doi:10.1016/j.pepi.2004.05.008 |
| [10] |
Nestola F, Gatta G D, Boffa B T. The effect of Ca substitution on the elastic and structural behavior of orthoenstatite[J]. American Mineralogist, 2006, 91: 809-815. Doi:10.2138/am.2006.1982 |
| [11] |
Nestola F, Ballaran T B, Balic-Zunic T, et al. The high-pressure behavior of an Al-and Fe-rich natural orthopyroxene[J]. American Mineralogist, 2008, 93: 644-652. Doi:10.2138/am.2008.2693 |
| [12] |
Nestola F, Ballaran T B, Angel R J, et al. High-pressure behavior of Ca/Na clinopyroxenes:the effect of divalent and trivalent 3d-transition elements[J]. American Mineralogist, 2010, 95: 832-838. Doi:10.2138/am.2010.3396 |
| [13] |
Jahn S. High-pressure phase transitions in MgSiO3 orthoenstatite studied by atomistic computer simulations[J]. American Mineralogist, 2008, 93: 528-532. Doi:10.2138/am.2008.2710 |
| [14] |
Zhang J S, Reynard B, Montagnac G, et al. Pressure-induced Pbca-P21/c phase transition of natural orthoenstatite:Compositional effect and its geophysical implications[J]. American Mineralogist, 2013, 98(5-6): 986-992. Doi:10.2138/am.2013.4345 |
| [15] |
Zhang J S, Reynard B, Montagnac G, et al. Pressure-induced Pbca-P21/c phase transition of natural orthoenstatite:the effect of high temperature and its geophysical implications[J]. Physics of the Earth and Planetary Interiors, 2014, 228: 150-159. Doi:10.1016/j.pepi.2013.09.008 |
| [16] |
Li B, Kung J, Liu W, et al. Phase transition and elasticity of enstatite under pressure from experiments and first-principles studies[J]. Physics of the Earth and Planetary Interiors, 2014, 228: 63-74. Doi:10.1016/j.pepi.2013.11.009 |
| [17] |
Finkelstein G J, Dera P K, Duffy T S. Phase transitions in orthopyroxene (En90) to 49 GPa from single-crystal X-ray diffraction[J]. Physics of the Earth and Planetary Interiors, 2015, 244: 78-86. Doi:10.1016/j.pepi.2014.10.009 |
| [18] |
Angel R J, Hugh-Jones D A. Equations of state and thermodynamic properties of enstatite pyroxenes[J]. Journal of Geophysical Research, 1994, 99: 19777-19783. Doi:10.1029/94JB01750 |
| [19] |
Li B, Neuville D R. Elasticity of diopside to 8 GPa and 1073 K and implications for the upper mantle[J]. Physics of the Earth and Planetary Interiors, 2010, 183: 398-403. Doi:10.1016/j.pepi.2010.08.009 |
| [20] |
Duffy T S, Vaughan M T. Elasticity of enstatite and its relationship to crystal structure[J]. Journal of Geophysical Research, 1988, 93(B1): 383-391. Doi:10.1029/JB093iB01p00383 |
| [21] |
秦善. 结构矿物学[M]. 北京: 北京大学出版社, 2011: 110-111.
|
| [22] |
Giannozzi P, Baroni S, Bonini N, et al. Quantum espresso:a modular and open-source software project for quantum simulations of materials[J]. Journal of Physics-Condensed Matter, 2009, 21(39): 1-19. |
| [23] |
Ceperley D M, Alder B J. Ground state of the electron gas by a stochastic method[J]. Physical Review Letters, 1980, 45(7): 566-569. Doi:10.1103/PhysRevLett.45.566 |
| [24] |
Perdew J P, Zunger A. Self-interaction correction to density-functional approximations for many-electron systems[J]. Physical Review B, 1981, 23(10): 5048-5079. Doi:10.1103/PhysRevB.23.5048 |
| [25] |
Vanderbilt D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism[J]. Physical Review B, 1990, 41(11): 7892. Doi:10.1103/PhysRevB.41.7892 |
| [26] |
Monkhorst H J, Pack J D. Special points for Brillouin-zone integrations[J]. Physical Review B, 1976, 16(4): 1748-1749. |
| [27] |
Molin G M. Crystal-chemical study of cation disordering in Al-rich and Al-poor orthopyroxenes from spinel lherzolite xenoliths[J]. American Mineralogist, 1989, 74: 593-598. |
| [28] |
Thompson R M, Downs R T. Model pyroxenes I:Ideal pyroxene topologies[J]. American Mineralogist, 2003, 88(4): 653-666. Doi:10.2138/am-2003-0419 |
| [29] |
Musgrave M J P. Crystal acoustics:introduction to the study of elastic waves and vibrations in crystals[M]. San Francisco: Holden-Day, 1970: 83-86.
|
| [30] |
Yu Y G, Wentzcovitch R M, Angel R J. First principles study of thermodynamics and phase transition in low-pressure (P21/c) and high-pressure (C2/c) clinoenstatite MgSiO3[J]. Journal of Geophysical Research, 2010, 115: B02201. |
| [31] |
Xu J, Zhang D, Fan D, et al. Phase transitions in orthoenstatite and subduction zone dynamics:effects of water and transition metal ions[J]. Journal of Geophysical Research:Solid Earth, 2018, 123: 2723-2737. Doi:10.1002/2017JB015169 |
| [32] |
Zhang J S, Bass J D. Single crystal elasticity of natural Fe-bearing orthoenstatite across a high-pressure phase transition[J]. Geophysical Research Letters, 2016, 43: 8473-8481. Doi:10.1002/2016GL069963 |
 2020, Vol. 37
2020, Vol. 37 


