准确的网络流量分类是众多网络活动的基础,许多互联网服务提供商将流量分配到相关服务类别的能力视为优先事项。因为对网络应用的了解能使网络运营商更好地规划、预算和计费,还可以跟踪不同用户群的增长并设计网络以满足不同的需求。
传统的流量识别方法主要有端口识别与深度包检测(deep packet inspection, DPI)。在互联网发展初期,应用协议比较单一, 协议在服务器端均使用固定的传输层端口号,并都在互联网号码分配机构(The Internet Assigned Numbers Authority, IANA)[1]上进行注册,如HTTP协议使用80端口,为Web应用;25端口为SMTP,110端口为POP3,均为Mail应用等。而随着互联网的发展,越来越多的私有、非标准协议出现,且没有在IANA中注册使用的端口,新型应用又多采用动态端口技术,这些变化使得端口识别的准确度已经低于50%[2]。因此自2000年后,通过提取流量载荷的特征信息进行识别的DPI方法逐渐受到青睐,不仅识别的准确度高,而且在稳定性等方面也取得了令人满意的效果。可由于新应用层出不穷、数据包中的特征字符串复杂多变,网络业务流量巨大,DPI技术已经很难适应如今的高速网络,此外DPI也难以有效识别越来越多的加密流量。
基于机器学习的流量分类通过流量在传输中的统计特征进行分类,能有效克服传统方法的问题。自Paxson和Floyd[3-4]对互联网流量统计特征的开创性研究以来,已经开展了许多研究来开发使用机器学习技术进行流量分类。Zuev和Moore[5]提出基于朴素贝叶斯(naïve Bayes, NB)的流量分类器,该方法假设所有统计特征间相互独立且服从高斯分布,然而真实的流量数据很难满足上述条件。因此,该方法流量分类的整体准确率仅有65%。之后Moore和Zuev[6]使用基于关联的快速过滤(fast correlation-based filter, FCBF)对特征进行筛选,并采用核估计技术对NB算法进行改进,将分类准确率提高到95%,但使用核密度估计无法保证分类结果的稳定性。Roughan等[7]介绍两种简单的机器学习方法处理流量分类,包括K近邻(k-nearest neighbor, K-NN)和线性判别分析(linear discriminant analysis, LDA)。K-NN方法需要单独计算训练样本和未识别的流量之间的相似性,不仅计算开销大,且容易受到噪声的干扰;LDA方法通常需要复杂的预处理操作,产生大量额外开销。有监督的机器学习方法,都需要将使用的数据预先分类好,所以有些学者将无监督的机器学习算法应用到网络流量分类中。McGregor等[8]使用EM算法对网络流量进行聚类分析, 表明可以利用流量模式相似性将观察到的流分组到分层群集中,证明无监督机器学习对粗略统计流量分类的有效性。Erman等[9-10]应用多种聚类算法,包括K-Means、DBSCAN和AutoClass算法, 分类准确度均优于NB算法,而且因为不需要训练数据的标签,所以能够识别出未出现过的新类别流量。
特征选择是从原始特征中选择出一些最有效特征以降低数据集维度的过程, 它是提高学习算法性能的一个重要手段[11], 上述算法均对数据集整体进行特征选择,对所有类别采用统一的特征子集。但使整体性能达到最优的特征子集确不一定是使特定类别流量达到最优的特征子集,对于所占权重不大的类别,甚至完全不能体现该类流量的数据特征,这降低了分类性能可达的上限。
本文对此提出基于改进一对一算法的网络流量分类模型。首先采用一对一的思想将原本流量多分类任务拆解为多个二分类的子任务,每个任务对任意两类流量进行分类,将通常的对全部数据集进行特征选择改为每个子任务分别进行特征选择,充分挖掘每类流量的数据特征,有利于提升分类性能。最后采用Stacking结合策略将所有的分类结果作为数据特征再次使用机器学习算法进行训练和分类,得到最后的分类结果。使用Moore数据集验证模型的可行性,结果表明多种机器学习算法与特征选择算法应用于该模型的准确度较经典模型相比均有提升。
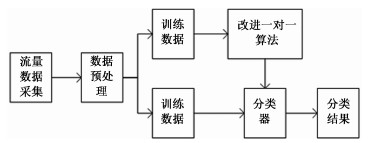
1 网络流量分类系统流程网络流量分类的系统流程如图 1所示,分为训练与测试两个阶段。在训练阶段,包含流量数据采集、数据预处理与流量分类3个步骤。
|
Download:
|
| 图 1 网络流量分类系统 Fig. 1 Network traffic classification system | |
流量数据采集:首先从网络中采集数据包的头部信息,对流量特征(如分组到达时间间隔、分组数量、平均分组长度等等)进行统计生成原始数据集,本文中使用公开的网络流量数据集。
数据预处理:采集好的数据需要进行预处理,因为网路流量在采集过程中,部分数据会有所缺漏,需要填充数据,另外一些特征选择算法与分类算法要求数据是归一化的。经过预处理的数据称作训练数据集。
流量分类:处理好的训练数据集即可输入到学习器中进行训练,与经典模型中直接将机器学习算法作为学习器不同,本文使用改进的一对一算法构造学习器模型。此外,对于大部分的机器学习算法,为了降低算法复杂度和提高分类准确率,需要对输入数据先采用特征选择算法获取对分类最有利的最佳特征子集。
在测试阶段,采集、处理后的测试数据,输入到训练好的分类器中,即可得到分类结果。
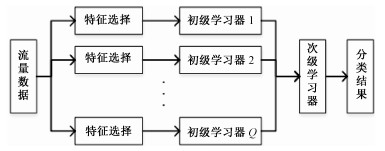
2 基于改进一对一算法的网络流量分类本文提出基于改进一对一算法的网络流量分类模型,将原本的多分类任务首先用一对一的思想拆解为多个子任务,每个子任务独立进行特征选择与流量分类,训练数据为任意两类流量,在分类时,子任务对于任意类别流量的判定结果均为用于训练的两类流量之一。所有子任务的预测结果使用Stacking结合策略得到最终的分类结果,分类模型如图 2所示。
|
Download:
|
| 图 2 基于改进一对一的流量分类模型 Fig. 2 Traffic classification model based on the improved one-versus-one method | |
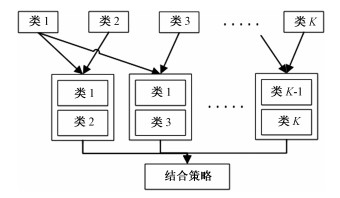
一对一算法可将二分类机器学习算法扩展到多分类,常用于多分类的支持向量机(support vector machine, SVM)[12],算法模型如图 3所示。对于有多个类别的数据,一对一算法将所有类别两两组合,使用每两类的训练样本构建类间的分类器。本文利用其思想构造流量分类模型,使其适用于更多的机器学习算法。并且在此基础上进行改进,将原本对整体数据的特征选择过程改进为对每个子学习器分别进行特征选择,有利于提升子学习器的准确度。
|
Download:
|
| 图 3 一对一算法 Fig. 3 One-versus-one algorithm | |
给定网络流量数据集D={(x1, y1), (x2, y2), …, (xm, ym)},K个网络流量类别C={c1, c2, …, cK},yi∈C表示样本的类别,xi表示样本的特征向量。
根据一对一法,共产生Q=K(K-1)/2个子任务。对于子任务Ti,包含特征选择与机器学习两部分,初始的输入数据为两类数据的集合Di,首先使用特征选择算法Γi求出数据集Di的最佳特征子集Si,并得到刷选后的数据集Di=Si(Di),之后输入到机器学习算法Yi的学习器中进行训练,得到分类器hi=Yi(Di)。各子任务的分类结果通过结合策略得到最终的分类结果,常用的结合策略为投票法,对于样本x,各子任务的分类结果为
| $ \bar{y}=\arg\max\limits _{c_{j} \in C} \sum\limits_{i=1}^{Q} I\left(\bar{y}_{i}=c_{j}\right). $ |
投票法设计简单有效,但会出现不可分区域的问题,从而降低分类的准确率。而且投票法并没有考虑各子任务的权重差异,通过学习器进行结合的学习法是一种更强大的的结合策略,本文使用学习法中的Stacking结合策略[13]。
Stacking模型分为两层,第1层为多个初级学习器,用于结合的第2层的分类器称为次级学习器。由图 2所示,在改进一对一算法的网络流量分类模型中,按一对一算法生成的子任务中的学习器就是初级学习器。Stacking先用初始数据集训练出初级学习器,初级学习器的分类结果组合成一个新的数据集作为次级学习器的输入。在新数据集中,每个初级学习器的输出称为次级学习器输入的一个特征,而初始样本的标签仍被当作样例标签。对于样本(x, y),次级学习器的输入形式为
| $ \left(\left(\bar{y}_{1}, \bar{y}_{2}, \cdots, \bar{y}_{Q}\right), \boldsymbol{y}\right). $ |
综上所述,改进模型的伪代码如下。
输入:
1) 训练集D={(x1, y1), (x2, y2), …, (xm, ym)};
2) 初级学习算法Yi, i=1, 2, …, Q;
3) 特征选择算法Γi, i=1, 2, …, Q;
4) 次级学习算法Y。
过程:
1) for i=1, 2, …, Q do
2) Si=Γ(Di)
3) hi=Yi(Γ(Di))
4) end for
5) D′=Ø
6) for t=1, 2, …, mdo
7) for i=1, 2, …, Q do
8) yit=hi(xt)
9) end for
10)
11) end for
12) h′=Y(D′)
输出:y=h′([hi(Si(x)), i=1, 2, …Q])。
对于一组特征选择算法和机器学习算法,若其应用于经典模型时,训练与测试阶段的计算复杂度分别为O(T1)和O(T2),则将其应用于改进模型中的初级学习器后,一对一算法将多分类任务拆分为K(K-1)/2个子任务,测试阶段的计算复杂度为O(K2T2),而对于训练阶段,每个子任务的样本数量是小于初始数据集的,所以复杂度也小于O(K2T1)。这里考虑流量是均匀分布的, 原始数据集的样本数为N,则每个子任务的数据量为2 N/K。若O(T1)与N成正比,则训练阶段的计算复杂度为O(KT1);若与N2成正比,则计算复杂度为O(T1)。此外,在用Stacking策略结合时,根据所选次级算法不同,会增加不同程度的计算复杂度。
3 实验 3.1 实验环境及数据集实验的硬件配置采用IntelCore(TM) i7-8700 K@ 3.70 GHz,16 GB RAM,平台采用64位的Windows10系统,实验工具主要使用Python和Weka。
为了验证分类系统的性能,需要适当地输入数据,本文使用Moore数据集[14]。Moore数据集使用网络监测器采集1 000个用户通过一条链路在24 h内的网络流量,原始流量集包含在两个链路方向上连接节点的所有全双工流量。由于原始流量集太大,通过随机抽样方法将其划分为10个子集。每个子集的采样时间几乎相同(每个大约1 680 s),这些非重叠随机样本在24 h间隔内均匀分布。Moore数据集中每条网络流样本都是从一条完整的TCP双向流抽象出来,共包含249项特征,其中,最后一项特征是每条网络流相对应的类别。Moore流量数据集共有12种应用类型,由于GAMES类流量的数量太少,无法有效分类,在本文实验中,不考虑该类流量。
3.2 评判标准通常在使用机器学习方法进行流量分类时,应根据测试数据集的实验结果估计模型的分类能力。根据样例的真实类别与学习器预测类别的组合划分为真正例、假正例、真反例、假反例4种情形,令TPi, FPi, TNi, FNi, 分别表示第i类对应的样例数。定义如下指标对分类模型进行评估:
1) 准确率
对于特定类别,准确率是指该类流量被正确分类的样本占被分为该类别的所有样本的比例,衡量的是分类系统对该类的查准率。
2) 召回率
对于特定类别,召回率是指该类流量被正确分类的样本占该类别原始总样本的比例,衡量的是分类系统对该类的查全率。
3) 总体准确度
总体准确度是指在识别正确的测试样例占总测试样例的比例,衡量系统的整体分类性能。
此外,还将分别使用训练和测试阶段的仿真运行时间衡量算法的计算复杂度。
3.3 实验结果为了验证改进模型的性能,分别将多种机器学习算法作为改进一对一算法的初级学习器进行仿真实验,并且与经典模型中这些算法直接用于流量分类的性能进行比较。采用的机器学习算法为:NB,SVM,C4.5决策树。特征选择算法为FCBF, 次级学习器算法为C4.5决策树。
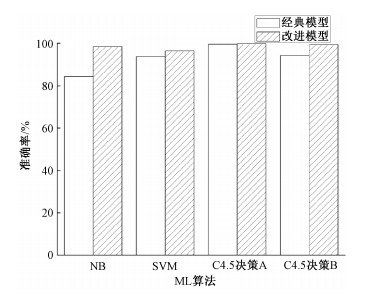
图 4展示不同机器学习算法在不同分类模型下的准确度。表 1展示数据集样本数为46 522时,算法在训练与测试阶段的运行时间,数据集中50%用于训练,50%用于测试。由结果可知,多种ML算法应用于改进模型时,准确度较经典模型相比有不同程度提升,但计算复杂度也变高了。其中NB的准确率由84.3%提升到98.4%,提升的幅度最大,说明模型对于弱学习器的提高效果更明显。SVM的性能提升较小,这是因为SVM本身是二分类任务,在应用到多分类任务中时,也会采用与本系统相同的一对一方法,但所有子任务使用同一特征子集,而本文所有子任务分别进行特征选择。决策树算法的准确度由图中C4.5决策树A所示,改进后准确度仅提升0.2%,在经典模型中已然达到99.5%。这是因为Moore数据集中的流量还是使用注册端口,所以按照端口识别已能达到95%以上的准确度,因此将端口号这一特征剔除后,再次用决策树算法分类,实验结果由C4.5决策树B所示,可以看到两种模型下,准确度分别下降为94.5%和99.2%。
|
Download:
|
| 图 4 不同分类模型的总体准确度 Fig. 4 Accuracies of different classification models | |
|
|
表 1 不同分类模型的计算复杂度 Table 1 Computational complexities of different classification models |
进一步观察改进模型对每一类流量的性能变化,表 2展示图 4中NB算法作为初级子任务时,不同模型下每个类别的分类准确率与召回率。从表中可以看出,大部分类别的准确率有所提升,WWW的准确率虽然有所下降,但是其召回率从84.9%大幅上升到99.6%。这说明将WWW误判为其他类的数量大大减少,作为数量占比达86.9%的流量类别,其查全率的提高对总体准确度的提高至关重要。在经典模型中,WWW、MAIL两种数据量较大的类别分类准确度都很高,都接近100%,FTP-DATA、DATABASE类在两种模型下的准确率与召回率均很高,说明数据类流量的统计特性独特,明显区分于其他类别。其余占比较小的流量分类性能都不太理想,这说明应用经典模型时,在网络协议流不平衡的环境下,分类器容易被流样本中大类流淹没,优先考虑流量占比较大类别的准确度,从而造成对小类流的识别率较低,甚至不能被发现。而在改进模型中,多数流量数量较小的类别准确率与召回率均得到显著提升,说明改进模型能有效处理流量不均问题。但改进后,INTERACTIVE和ATTACK这2种类型的准确率与召回率仍为0,说明当流量样本太少或数据特征极不明显时,基于统计的方法很难有效识别。
图 5展示多种特征选择算法应用于不同模型后的总体准确度,采用的特征选择算法分别为基于信息增益比(information gain ratio, IGR),基于对称不确定性(symmetrical uncert, SU),CFS (correlation-based feature selection)与FCBF,初级学习器为NB,次级学习器为C4.5决策树。由图可知,特征选择算法在改进模型中的分类准确度均优于经典模型。其中CFS与FCBF为多变量过滤式算法,其分类准确度显著高于作为单变量过滤数算法的SU和IGR,这是由于单变量过滤式算法在选取特征子集时,没有考虑到冗余特征的问题,降低了分类性能。
|
|
表 2 不同分类模型下各类流量的准确率和召回率 Table 2 Accuracies and recall rates of different classes under different classification models |

|
Download:
|
| 图 5 多种特征选择算法在不同分类模型的总体准确度 Fig. 5 Accuracies of different feature selection algorithms in different classification models | |
与本文提出的改进模型不同,大多数机器学习算法使用同一特征子集对数据降维。为了进一步验证改进一对一算法在特征学习中的优越性,将算法中的特征选择改为在预处理过程中对整个数据集进行特征选择,所有子任务使用同一特征子集进行仿真,并与改进模型中各子任务分别进行特征选择并比较。
表 3展示各子任务使用同一特征子集与不同特征子集时的分类准确度,因子任务数量过多,只列出部分子任务。可以看到各子任务的分类准确度均有不同程度提升,从而使整体的分类准确度得到提升。WWW类相关子任务的准确度提升不大,这是因为在整体特征选择时,会优先考虑占比较大的流量类, 对于WWW与MAIL的分类子任务,使用同一特征子集时,准确度就已达到99.8%。P2P、ATTACK类相关子任务的准确度提升明显,但相比于其他类别仍处于较低水平。需要注意的是,在使用同一特征集后,整体准确度仅为81.6%,比经典模型还要低2.7%,这是因为大多数子任务的训练数据都较少,而且对于子任务包含的两类流量,整体数据集的最佳特征子集并不是最利于分类的特征,造成大量子任务的误判,从而导致整体识别效果下降。
|
|
表 3 不同特征选择模式下的子学习器准确度 Table 3 Accuracies of base-learner in different feature selection modes |
本文基于改进一对一算法提出一种新的网络流量分类模型。首先采用一对一的方法将多分类任务拆解为多个二分类的子任务,每个子任务对任意两类流量进行分类,之后将所有子任务的分类结果作为输入数据再次输入到次级学习器中,得到最后的分类结果。本文使用moore数据集进行仿真实验,图 4,图 5显示机器学习算法与特征选择算法应用于改进模型后,较在经典模型中准确度有所提升,但通过表 1发现改进模型计算复杂度要高于经典模型。表 2具体展示系统对每类的分类情况,说明改进模型对于占比较小的类别能显著提升分类性能。表 3证实模型在特征选择上的优异性,子任务分别进行特征选择比使用同一特征子集的准确度高。
本文实验中,对于每一个子任务都采用了相同的特征选择算法和机器学习算法。而对于提出的模型,各子任务间相互独立,因此针对不同的子任务,可以使用不同的算法进行分类,此举可以进一步提高子任务的识别度,从而提升整个系统的准确度。对任意两个类别均建立分类子任务的复杂度较高,可在不影响识别性能的前提下,关闭部分子任务,降低复杂度。
| [1] |
IANA.IANA port number list[EB/OL]. (2003-06-14)[2018-10-18].http://www.iana.org/assignments/port-numbers.
|
| [2] |
Kim M, Won Y J, Hong J W. Application-level traffic monitoring and analysis on IP networks[J]. ETRI Journal, 2005, 27(1): 22-42. Doi:10.4218/etrij.05.0104.0040 |
| [3] |
Paxson V. Empirically derived analytic models of wide-area TCP connections[J]. IEEE/ACM Transactions on Networking, 1994, 2(4): 316-336. Doi:10.1109/90.330413 |
| [4] |
Paxson V, Floyd S. Wide area traffic:the failure of Poisson modeling[J]. IEEE/ACM Transactions on Networking, 1995, 3(3): 226-244. Doi:10.1109/90.392383 |
| [5] |
Zuev D, Moore A.Traffic classification using a statistical approach[C]//Proceedings of PAM'05. Berlin: Springer-Verlag, 2005: 321-324.
|
| [6] |
Moore A W, Zuev D. Internet traffic classification using Bayesian analysis techniques[J]. ACM Sigmetrics Performance Evaluation Review, 2005, 33(1): 50-60. Doi:10.1145/1071690.1064220 |
| [7] |
Roughan M, Sen S, Spatscheck O, et al. Class-of-service mapping for QoS: a statistical signature-based approach to IP traffic classification[C]//Proceedings of IMC'04.New York: ACM, 2004: 25-27.
|
| [8] |
Mcgregor A, Hall M, Lorier P, et al. Flow clustering using machine learning techniques[C]//Proceedings of PAM'04.Berlin: Springer-Verlag, 2004: 205-214.
|
| [9] |
Erman J, Arlitt M, Mahantii A.Traffic classification using clustering algorithms[C]//Proceedings of the 2006 International Conference on Sigcomm Workshop On Mining Network Data.New York: ACM, 2006: 281-286.
|
| [10] |
Erman J, Mahanti A, Arliyy M.Internet traffic identification using machine learning[C]//Proceedings of the 49th IEEE Conference on Global Telecommunications.San Francisco: IEEE, 2006: 1-6.
|
| [11] |
Yu L, Liu H.Feature selection for high-dimensional data: a fast correlation-based filter solution[C]//20th International Conference on Machine Learning.Washington DC: IMLS, 2003: 856-863.
|
| [12] |
Hsu C W, Lin C J. A comparison of methods for multi-class support vector machines[J]. IEEE Transactions on Neural Networks, 2002, 13(2): 415-425. Doi:10.1109/72.991427 |
| [13] |
Wolpert D H. Stacked generalization[J]. Neural Networks, 1992, 5(2): 241-259. |
| [14] |
Moore A, Zuev D, Crogan M, et al. Discriminators for use in flow-based classification[M]. London: Queen Mary University of London, 2005.
|
 2020, Vol. 37
2020, Vol. 37 


