2. 中国科学院大学, 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
对地观测技术的优势在于能够快速准确地获取人类地表活动信息[1],而遥感作为对地观测技术的一种,其应用范围越来越广泛,不仅在环境灾害防治、城市建设规划、气象预报等领域发挥重要作用[2],而且在考古遗址[3]、遥感卫星车辆检测[4]、气溶胶辐射观测[5]等方面的应用也越加普遍。虽然对地观测卫星的数量和成像能力已得到巨大提升,但由于各行各业对遥感影像数据的大量需求,使得成像卫星的资源仍相对稀缺。因此,研究如何充分利用卫星资源,以经济快捷的方式获取较高质量的遥感数据,就成为必要之举,也是本文要研究的多星成像任务规划问题。它是指考虑星上传感器成像能力、传感器的侧摆能力等因素,合理安排卫星,对区域目标制定成像方案[6-7]。
多星成像任务规划是一类极其复杂的组合优化问题[8], 同时在数学上也是一种NP—完全问题[9]。这类问题,国内外已有大量研究[10-11],通常包括模型建立和求解两部分。如Wolfe和Sorensen[12]将卫星成像任务规划问题映射为带时间窗约束的背包问题,建立整数规划模型;Song等[13]对单星成像规划问题建立非线性规划模型;贺仁杰等[14]对成像规划问题建立约束满足问题模型。而模型求解的方法多采用启发式算法,如模拟退火算法[14]、蚁群算法[15]、遗传算法[16]等。这些算法大都从解的邻域搜索最优解,容易陷入局部最优,得到次优解。虽然模拟退火算法对陷入局部最优有所改善,但计算效率不高。因此,为增强全局最优解的搜索能力,并兼顾计算效率,本文采用基因表达式编程来求解多星成像规划问题。
1 基因表达式编程算法简介基因表达式编程(gene expression programming, GEP)起源于遗传算法,但又结合了遗传编程的优点,是二者融合的产物[17]。它的染色体是由一个或多个基因组成,用固定长度的线性符号串来表示。每个基因也是由固定长度的线性符号串构成,包括头部和尾部两部分。表 1为染色体的构成。
|
|
表 1 染色体的构成 Table 1 Chromosome composition |
基因头部符号串包含函数符号和终止符;尾部符号串只包含终止符。长度为t的尾部和长度为h的头部满足公式
| $ t = h \times (n - 1) + 1, $ | (1) |
式中:n为函数符中的最大操作数目[18]。例如,“+”,“-”,“×”的操作数目都为2;Q代表平方根,它为一目运算符。对于函数符号集{+,-,×,Q }中最大操作数目为2,则n=2。
此外,基因表达式编程的多基因家族染色体中可以包含多个基因家族,基因家族之间按某种规则相互作用,而基因家族又可以包含多个基因。GEP的遗传算子有变异、逆串、插串、根插串、两点重组等,丰富的遗传算子和灵活的染色体结构使得GEP具有强大的应用功能。
2 多星成像模型的建立在研究区域目标多星成像时,需要进行卫星轨道的预报计算,本文采用应用广泛的SGP4(simplified general perturbations)模型,即简化常规摄动模型[19-20]求解卫星的位置和速度。然后再根据目标区域,结合过境卫星的侧摆能力和过境时间计算成像条带。在选取条带组成成像方案时,需要考虑约束性。
2.1 模型的约束条件分析模型的约束主要考虑卫星的成像约束,表 2是本文考虑的卫星成像的约束规则。
|
|
表 2 卫星成像的约束规则 Table 2 Constraint rules of satellite imaging |
卫星过境时,所携带的传感器的不同成像模式都有可能参与成像,本文将传感器以不同的成像模式过境称为逻辑轨道。所以逻辑上来讲,一颗有多种模式传感器的卫星过境一次就会产生多个逻辑轨道。如果传感器不同的成像模式不能同时参与成像,就只能选取其中之一的逻辑轨道产生的条带参与成像,否则,便不满足表 2卫星约束中的1)、2)约束条件。同一逻辑轨道产生的多个条带,只能选择其中一个参与成像,否则便不满足表 2卫星约束中的3)、4)约束条件。如果参与成像的条带之间重叠范围过大,会造成极大的资源浪费。所以需要检查选取的条带是否满足成像覆盖约束。通常设定一个阈值OverLap为一个常数,两个条带分别为Stripx, Stripy,二者的重叠部分为
| $ {\rm{Intersection}} = {\rm{Stri}}{{\rm{p}}_x}{\rm{ }} \cap {\rm{Stri}}{{\rm{p}}_y}. $ | (2) |
设重叠区域的面积为Aintersect,条带Stripx的面积为AStripx,条带Stripy的面积为AStripy,则应满足约束条件
| $ {A_{{\rm{ intersect }}}}/{A_{{\rm{ Strip}}{{\rm{ }}_x}}} < {\rm{OverLap}}, $ |
和
| $ {A_{{\rm{ intersect }}}}/{A_{{\rm{ Strip}}{{\rm{ }}_y}}} < {\rm{OverLap}}. $ | (3) |
为便于模型的建立及求解,本文将一条成像条带看作是一个元任务,作为模型的数据输入[14]。它包含卫星、传感器、成像范围、成像模式、成像时间等重要信息。决定成像任务规划方案优劣的因素有多个,主要包括:目标区域的覆盖率;成像方案的起止时间;参与成像的传感器个数;成像过境的轨道数;成像的条带数。其中任意因素皆可作为成像任务优化的目标,多星成像任务规划是一个多目标优化问题。其数学模型一般描写为如下形式:
| $ \mathit{\boldsymbol{Z}} = \mathit{\boldsymbol{F}}(\mathit{\boldsymbol{X}}) = \left( {\begin{array}{*{20}{c}} {{\rm{max}}({\rm{min}}){f_1}(\mathit{\boldsymbol{X}})}\\ {{\rm{max}}({\rm{min}}){f_2}(\mathit{\boldsymbol{X}})}\\ \vdots \\ {{\rm{max}}({\rm{min}}){f_k}(\mathit{\boldsymbol{X}})} \end{array}} \right), $ | (4) |
| $ \mathit{\boldsymbol{ \boldsymbol{\varPhi} }}(\mathit{\boldsymbol{X}}) = \left( {\begin{array}{*{20}{c}} {{\varphi _1}(x)}\\ {{\varphi _2}(x)}\\ \vdots \\ {{\varphi _m}(x)} \end{array}} \right) \le \mathit{\boldsymbol{G}} = \left( {\begin{array}{*{20}{c}} {{g_1}}\\ {{g_2}}\\ \vdots \\ {{g_m}} \end{array}} \right). $ | (5) |
式中:X=[x1, x2, …, xn]T为决策变量的向量, Z= F(X)为目标向量,Φ(X)≤G为约束向量。
下面是本文选取的一些影响因素作为成像规划的优化目标来设计的收益函数。首先以条带数最少为优化目标,设成像目标的覆盖率为PCov,Ws为条带数影响因子,Strips为成像方案条带数,N′s为逻辑过境轨道数,则收益函数为
| $ P = {P_{{\rm{Cov}}}} \times 0.1 + \left( {1 - {W_{\rm{S}}} \times \left( {\frac{{{\rm{Strip}}{_s}}}{{N_{\rm{s}}^\prime }}} \right)} \right). $ | (6) |
以成像周期最短为优化目标,设成像规划输入的时间段为Tstart至Tend, 成像方案的实际起止时间分别为T′start和T′end,任务完成时间的影响因子为wt,则收益函数为
| $ P = {P_{{\rm{Cov}}}} \times \left( {1 - {W_{\rm{t}}} \times \left( {\frac{{T_{{\rm{end}}}^\prime - {T_{{\rm{start}}}}}}{{{T_{{\rm{end}}}} - {T_{{\rm{start}}}}}}} \right)} \right). $ | (7) |
以轨道数最少为优化目标,设过境轨道数影响因子为wo,经过预处理后得到的实际过境轨道数为No,实际成像方案中,过境轨道数为N′o,则收益函数为
| $ P = {P_{{\rm{Cov}}}} \times \left( {1 - {W_{\rm{o}}} \times \left( {\frac{{N_{\rm{o}}^\prime }}{{{N_{\rm{o}}}}}} \right)} \right). $ | (8) |
以上是成像规划的单目标优化,而为了降低模型的复杂度,本文采用线形加权法,将多目标优化问题转化为单目标的优化[21]。虽然影响成像方案优劣的因素有多种,但主要考虑时间成本和卫星成本,而这些因素可由成像周期、成像轨道数、参与成像传感器数等优化目标反映出来,所以本文设计出包含成像周期、成像轨道数、参与成像传感器数等优化目标的综合收益函数。设总传感器数对收益的影响因子为Wc, 参与成像的传感器数Sen′N,过境的总传感器数SenN,则收益函数为
| $ \begin{array}{l} P = {P_{{\rm{Cov}}}} \times \left( {\left( {1 - {W_t} \times \left( {\frac{{T_{{\rm{end}}}^\prime - {T_{{\rm{start}}}}}}{{{T_{{\rm{end}}}} - {T_{{\rm{start}}}}}}} \right)} \right) + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {1 - {W_{\rm{o}}} \times \left( {\frac{{N_{\rm{o}}^\prime }}{{{N_{\rm{o}}}}}} \right)} \right) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\left( {1 - {W_{\rm{c}}} \times \left( {\frac{{ {\rm{Sen}} _N^\prime }}{{ {\rm{Sen}}{ _N}}}} \right)} \right)} \right)/3. \end{array} $ | (9) |
假设有L颗卫星, Li(i=1, 2, …, L)为第i颗卫星过境次数,si为第i颗卫星载有的传感器数,Mji为第j个传感器成像模式数;设第i颗卫星的第j个传感器第k个成像模式产生LSMPi, j, k个条带。则所有卫星过境产生的逻辑轨道数为
| $ \sum\nolimits_{i = 1}^L {{L_i}} \sum\nolimits_{j = 1}^{{s_i}} {M_j^i} . $ | (10) |
逻辑轨道产生的可能成像的总条带数为
| $ \sum\nolimits_{i = 1}^L {{L_i}} \sum\nolimits_{j = 1}^{{s_i}} {\sum\nolimits_{k = 1}^{M_j^i} {{\rm{LSM}}{{\rm{P}}^{i,j,k}}} } . $ | (11) |
进一步简化分析,将经过预处理后得到的过境逻辑轨道数设为n, 设每一过境轨道可能的成像条带个数分别为s1, s2, …, sn。设成像方案数为F(n, s), 一般地可以推断出[16]
| $ \begin{array}{*{20}{l}} {F(n,s) = \sum\nolimits_{k = 1}^n {\prod\nolimits_{i = 1}^k {C_{{s_i}}^1} } + \sum\nolimits_{k = 2}^n {\prod\nolimits_{i = 2}^k {C_{{s_i}}^1} } + \cdots + }\\ \ \ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\nolimits_{k = n}^n {\prod\nolimits_{i = n}^k {C_{{s_i}}^1} } } \end{array} $ | (12) |
式中:∏i=1kCsi1的第一部分为求积符号,而Csi1为数学上排列组合符号。
3 算法求解 3.1 解的编码设计本文设计了包含两个基因家族的染色体,每一个基因家族包含多个基因。基因的头部h=0,由式(1)可得尾部t=1,故基因长度等于1。
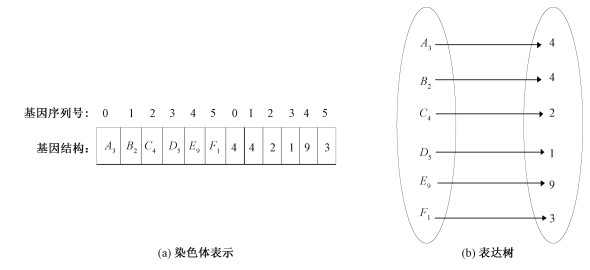
本文首先将产生的所有逻辑轨道划分为不同的集合,逻辑轨道集合的数量即是基因家族包含的单基因的数量,每个逻辑轨道集合包含的多个逻辑轨道相互冲突,不能同时参与成像。第一个基因家族中单个基因代表从逻辑轨道集合里被选中的逻辑轨道,另一个基因家族中的单个基因代表由上一个基因家族中相对应的逻辑轨道产生的条带集中被选中的参与成像的条带。这样的设计就可以满足表 2中卫星约束的相关条件。图 1为染色体的结构。
|
Download:
|
| 图 1 染色体结构 Fig. 1 Chromosome structure | |
倒置这一遗传算子能够增强算法对于解空间的搜索能力,同时对于染色体结构的破坏性也较大,不利于保留优良基因。为此本文引入知识库,该知识库包含了种群在进行迭代操作前的较优的小部分个体。设每次迭代产生的种群中最优个体为X,知识库中最优个体为Y,若X的适应度函数值(自适应值)大于Y,则将种群中比Y优的个体加入到知识库,替换掉知识库中次于Y的个体;若X的适应度函数值小于Y,则用知识库中所有优于X的个体置换掉种群里最差的一部分个体。此操作保证了参与迭代计算的种群个体始终是较优的,也有利于保留每次迭代产生的最优个体,避免最优解丢失。
3.3 算法求解过程在算法流程中染色体的自适应值也就是优化目标的收益函数值,收益函数可见式(6)~式(9)。具体遗传算子如下:
1) 交叉:先用轮盘赌注的方法选择个体,然后采取两点重组的方式进行交叉。当第1条染色体的逻辑轨道和第2条染色体的逻辑轨道进行交换时(交换的逻辑轨道必须属于同一逻辑轨道集,如逻辑轨道集B中的B1、B2), 相应的条带也得进行交换,这样保证了染色体始终满足表 2中卫星约束的相关条件。
2) 变异:当执行变异操作时,先进行逻辑轨道的变异,再从变异的逻辑轨道产生的条带中选取新的条带。
3) 倒置:在第1个基因家族中随机选取2个基因,将二者内的基因片段倒置,相对应的第1个基因家族中的基因片段也进行倒置。这一操作可能使基因非法,所以需要对倒置的基因片段进行检验,如果条带号超出对应的逻辑轨道产生的条带范围,则基因非法,重新选取条带,使基因合法。
此外,为了防止条带之间的重叠率过大而造成重复拍摄,还应做重叠率约束性检验。本文的做法是:
1) 在染色体所包含的所有条带集{S1, S2, …,Sn}中,按顺序遍历条带Si(i=1, 2,…,n),若遍历完所有条带,遍历结束,转4);否则转2)。
2) 依次查验条带Si与第i个之前的所有条带Sj(j=1, 2,…,i-1)是否满足重叠率约束条件,满足转1);不满足,在Si对应的逻辑轨道里产生的条带集里重新选取条带,若选取的条带Si与Sj(j=1, 2,…,i-1)满足重叠率约束条件,转1);否则,转3)。
3) 比较条带Si,与Sj(j=1, 2,…,i-1)对目标区域覆盖率的大小,若Si的较小,将Si设置为空,转1);若Sj的较小,将Sj设置为空, 继续比较剩余的条带Sj,直至j=i-1时,比较结束,转1)。
4) 检验结束,输出结果。
基因表达式编程与遗传算法的流程[22]类似,综合上文可得图 2为本文的算法流程图。

|
Download:
|
| 图 2 算法流程图 Fig. 2 Flow chart of the algorithm | |
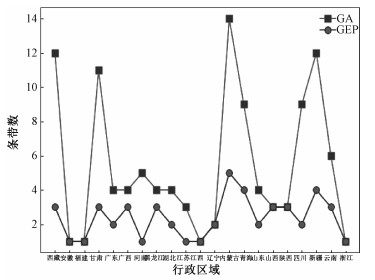
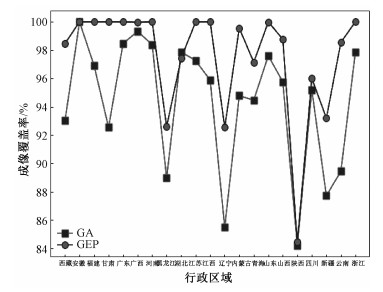
本文的仿真实验,采用NetBeans软件以及java语言编程,在World Wind Java基础上实现了多星成像任务规划算法,规划方案显示等功能。为验证本文算法的性能并与文献[16]中的遗传算法作对比,首先选取多个行政区,作为目标观测区域。同一目标观测区域调用两种算法时,输入参数相同,即选取的卫星、规划起止时间,收敛条件均相同,以成像方案的条带数最少作为优化目标。为了更直观地对比调用两种算法得出的成像方案的覆盖率、条带数,分别将结果整理为图 3、图 4。
|
Download:
|
| 图 3 观测次数对比 Fig. 3 Comparison of the observation times | |
|
Download:
|
| 图 4 成像覆盖率对比 Fig. 4 Comparison of the imaging coverage | |
由图 3、图 4可知,基因表达式编程GEP相对于遗传算法GA所得的观测方案,不仅条带数均少于后者,而且覆盖率大于后者。从观测次数(条带数)以及目标区域覆盖率两项指标而言,基因表达式算法得出的成像方案是较优的。在计算耗时上,对于大多数目标区域GEP计算用时均比GA要长,这是因为遗传算法在迭代过程中出现种群退化或停滞,然后过早地结束迭代计算;再者,在GEP的迭代计算过程中,本文引入倒置这一遗传算子,增加了计算量。但总体而言,GEP对大多数目标区域的计算用时在90 s内,是一种较为理想的结果。
继续选取内蒙古作为观测区域,每两天作为时间间隔,逐渐增加观测天数,并追踪目标区域观测情况。将结果整理成图 5,可知GEP算法对观测区域随观测天数的增加,其覆盖率增加得较快,且约两周后达到顶峰,即覆盖率为99.782%,并处于稳定状态。而GA算法对观测区域的覆盖率虽然也在随观测天数的增加而增加,但起伏较大,达到最优解的周期较长,而且不稳定。另外,GA算法求得最优解的覆盖率为96.442%,低于GEP的最优解。以上说明,GEP应用于多星成像任务规划问题,具有全局搜索能力强、鲁棒性较佳等优点, 并极大提高了解的精度。

|
Download:
|
| 图 5 覆盖率变化趋势 Fig. 5 The coverage changes | |
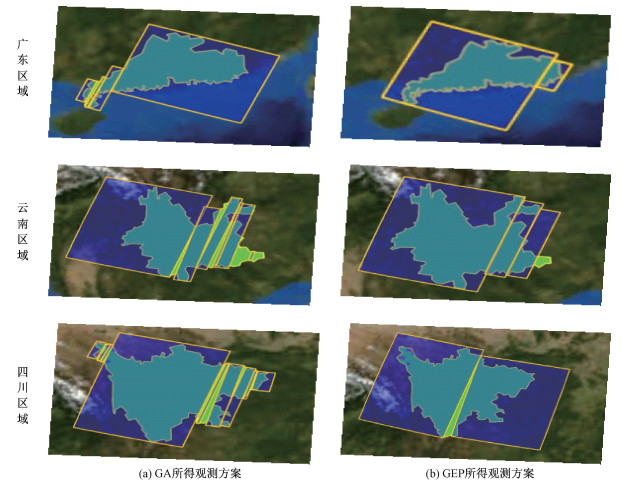
对广东、云南、四川等区域进行成像规划仿真显示。图 6直观显示了基因表达式编程所得的成像任务规划方案较佳。
|
Download:
|
| 图 6 观测方案的仿真显示 Fig. 6 Simulating display of the observation schemes | |
多星成像规划问题的研究对于卫星资源的充分利用及快速获取区域数据具有重要意义。本文结合实际应用,对面向区域目标的多星成像规划进行研究,首次用基因表达式编程GEP进行求解,并在算法过程中引入知识库保证参与迭代计算的种群是较优的。结果表明,本文算法求解精度高,鲁棒性较佳,相比遗传算法性能显著。但是,理论上讲,GEP计算效率是较高的,本文用于求解多星成像规划问题时,计算效率并未完全挖掘出来;此外,对于卫星的侧摆,只考虑了左右侧摆,未考虑卫星的前后侧摆,这些有待于进一步研究和探索。
| [1] |
江威, 何国金, 彭燕, 等. 夜光遥感在"一带一路"战略中的应用潜力展望[J]. 中国科学院大学学报, 2017, 34(3): 296-303. |
| [2] |
冯健翔. 人工智能航天应用研究[M]. 北京: 宇航出版社, 1999.
|
| [3] |
公雪霜, 于丽君, 聂跃平, 等. 辽宁西部地区先秦时期聚落遗址空间格局分析[J]. 中国科学院大学学报, 2016, 33(3): 373-379. |
| [4] |
袁益琴, 何国金, 王桂周, 等. 背景差分与帧间差分相融合的遥感卫星视频运动车辆检测方法[J]. 中国科学院大学学报, 2018, 35(1): 50-58. |
| [5] |
张凤霞, 李正强, 李凯涛, 等. 京津唐地区气溶胶直接辐射强迫的遥感观测[J]. 中国科学院大学学报, 2016, 33(2): 155-161. |
| [6] |
陈克伟, 安蓓, 王炎娟, 等. 基于PDDL的成像卫星任务规划建模[J]. 兵工自动化, 2008, 27(12): 41-44. Doi:10.3969/j.issn.1006-1576.2008.12.016 |
| [7] |
Lematre M, Verfaillie G, Jouhaud F, et al. Selecting and scheduling observations of agile satellites[J]. Aerospace Science and Technology, 2002, 6(5): 367-381. Doi:10.1016/S1270-9638(02)01173-2 |
| [8] |
经飞, 王钧, 李军, 等. 面向海洋观测的成像卫星任务规划方法[J]. 中国空间科学技术, 2011, 31(2): 72-78. |
| [9] |
Pinedo M L. Scheduling:theory, algorithms, and systems[M]. 3rd ed. Berlin: Spring, 2008.
|
| [10] |
王建江, 朱晓敏, 吴朝波, 等. 面向应急条件的多星动态调度方法[J]. 航空学报, 2013, 34(5): 1151-1164. |
| [11] |
Zhu K J, Li J F, Baoyin H X. Satellite scheduling considering maximum observation coverage time and minimum orbital transfer fuel cost[J]. Acta Astronautica, 2010, 66(1/2): 220-229. |
| [12] |
Wolfe W J, Sorensen S E. Three scheduling algorithms applied to the earth observing systems domain[J]. Management Science, 2011, 46(1): 148-166. |
| [13] |
Song D, Frank A, Stappen V, et al. An exact algorithm optimizing coverage-resolution for automated satellite frame selection[C]//IEEE International Conference on Robotics and Automation, 2004: 63-70.
|
| [14] |
贺仁杰, 李菊芳, 姚锋, 等. 成像卫星任务规划技术[M]. 北京: 科学出版社, 2011: 33-36.
|
| [15] |
朱政霖, 马广彬, 黄鹏, 等. 基于任务分解的多星成像规划模型建立与求解[J]. 航天器工程, 2018, 27(2): 6-13. Doi:10.3969/j.issn.1673-8748.2018.02.002 |
| [16] |
韩琼, 章文毅. 多星联合成像编程技术研究[J]. 遥感信息, 2013, 28(4): 19-23, 56. Doi:10.3969/j.issn.1000-3177.2013.04.004 |
| [17] |
常盛, 郑世钰. 通用型信息管理系统的探索与研究[J]. 硅谷, 2011(24): 82. |
| [18] |
彭昱忠, 元昌安, 麦雄发, 等. 基因表达式编程的理论研究综述[J]. 计算机应用研究, 2011, 28(2): 413-419, 438. Doi:10.3969/j.issn.1001-3695.2011.02.003 |
| [19] |
Hoots F R, Roehrich R L. Models for propagation of NORAD element sets[R]. Spacetack Report No.3, 1980: 1-79.
|
| [20] |
周岳昆, 章文毅. 基于影像浏览技术的卫星成像编程申请服务的实现[J]. 微计算机信息, 2010, 26(18): 21-23, 31. Doi:10.3969/j.issn.2095-6835.2010.18.009 |
| [21] |
刘华伟, 陈耀元, 叶莹. 多目标优化的新方法:幂加权和法及数值仿真[J]. 武汉理工大学学报(交通科学与工程版), 2007, 31(5): 835-838. Doi:10.3963/j.issn.2095-3844.2007.05.021 |
| [22] |
梁旭, 黄明. 现代智能优化混合算法及其应用[M]. 北京: 电子工业出版社, 2011: 34-35.
|
 2020, Vol. 37
2020, Vol. 37 


