2. Institutes for Robotics and Intelligent Manufacturing, Chinese Academy of Sciences, Shenyang 110169, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
2. 中国科学院机器人与智能制造创新研究院, 沈阳 110169;
3. 中国科学院大学, 北京 100049
With the discovery of more and more mineral types on the seabed, such as manganese nodule, submarine sulfide, and polymetallic concretion, underwater mining has become a promising hot spot to meet the needs of future mineral resources. In Fig. 1 we show the main structure of underwater mining system which is composed of underwater mining robot, mother ship, and ore-raising system[1-2]. For underwater mining robot moving autonomously on the seabed, the underwater navigation system is a key part of the underwater mining robot to ensure the robot mines efficiently and accurately.

|
Download:
|
|
Fig. 1 Structure of the underwater mining system |
|
The underwater navigation is a challenging research problem because of unavailability of global positioning system (GPS) under water[3]. Currently, most underwater vehicles are generally equipped with long baseline (LBL) acoustic positioning system and dead reckoning (DR) as an integrated navigation system. LBL/DR integrated navigation system is a modern navigation system, which combines the accuracy of the LBL and the stability of the DR[4]. Although there are many navigation algorithms of data fusion of LBL and DR, most of them can not be applied to the underwater mining navigation because underwater mining robot makes a lot of noise when it begins to mine. So LBL navigation system receives a lot of noise resulting in its accuracy declining. Furthermore, the underwater mining navigation is a strong non-linear model. To solve above problems, the underwater mining navigation algorithm of data fusion has been developed a lot. For instance, Yeu et al.[1] put forward a method of data fusion based on extending Kalman filter (EKF). It transforms non-linear model to linear model by solving Jacobian matrix. The non-linear problem of navigation system is solved to some extent[1]. Wang et al.[5] proposed a navigation system based on adaptive UKF. It transforms nonlinear model to linear model by using unscented transformation and adjusting error matrix by adaptive algorithm. However, these methods mentioned above are not qualified for strong non-Gaussian and nonlinear problems in underwater mining navigation system. So, a new navigation algorithm is needed. As we know, particle filter (PF) was introduced by Doucet et al.[6] to solve nonlinear and non-Gaussian problems. An improved PF was proposed by Carpenter et al.[7] by stratified sampling and implementing sampling importance resampling (SIR) with the method based on simulating order statistics. Although the particle degeneracy is solved by implementing SIR, a new problem of particle impoverishment is brought[8]. So, an improved PF is presented by Chen et al.[9] to deal with the problems of particle degeneration and particle impoverishment in traditional PF. Currently it is an ideal solution to particle degeneracy and particle impoverishment by introducing a better resampling algorithm. The most frequently used resampling algorithms are multinomial resampling[10-11], stratified resampling[10-12], systematic resampling[10, 12], and residual resampling[10-12]. The resampling algorithms mentioned above alleviate the problem of particle degeneracy, but they also bring the new problem of particle impoverishment.
Therefore, in this study, a new resampling algorithm is proposed. It hardly brings the problem of particle impoverishment. Meanwhile, it alleviates the problem of particle degeneracy. Then a new underwater navigation algorithm which combines the improved PF and underwater mining model is introduced to improve the accuracy of underwater mining navigation.
1 Background 1.1 The navigation model of underwater mining robotIn this study, the navigation model of underwater mining robot is described as follows. The state vector is defined as X=[x, y, ϕ, u, v, α]T, where x, y, and ϕ are north position, east position, and heading angle in the navigation frame, respectively, u and v are the forward velocity and starboard velocity in the vehicle reference frame, and α is the angular velocity. A first-order kinematic model is P used here. The process model is defined as
| $ \begin{array}{*{20}{c}} {{x_k} = {x_{k - 1}} + [({v_{k - 1}} + {P^5}){\rm{cos}}({\phi _{k - 1}} + {P^3}) + }\\ {({u_{k - 1}} + {P^4}){\rm{sin}}({\phi _{k - 1}} + {P^3})] \cdot {\rm{d}}t + {P^1},} \end{array} $ | (1) |
| $ \begin{array}{*{20}{c}} {{y_k} = {y_{k - 1}} - [({v_{k - 1}} + {P^5}){\rm{sin}}({\phi _{k - 1}} + {P^3}) + }\\ {({u_{k - 1}} + {P^4}){\rm{cos}}({\phi _{k - 1}} + {P^3})] \cdot {\rm{d}}t + {P^2},} \end{array} $ | (2) |
| $ {{\phi _k} = {\phi _{k - 1}} + ({\alpha _{k - 1}} + {P^6}) \cdot {\rm{d}}t + {P^3},} $ | (3) |
| $ {{u_k} = {u_{k - 1}} + {P^4},} $ | (4) |
| $ {{v_k} = {v_{k - 1}} + {P^5},} $ | (5) |
| $ {{\alpha _k} = {\alpha _{k - 1}} + {P^6},} $ | (6) |
where P is the process noise.
The observation vector is defined as Z=[x, y, ϕ, u, v, α]T, and then the observation model is defined as
| $ {\mathit{\boldsymbol{Z}}_k} = {\mathit{\boldsymbol{X}}_k} + \mathit{\boldsymbol{Q}}, $ | (7) |
where Q is the observation noise.
Here, the vertical movement is neglected due to its tininess. In this work, the underwater mining navigation algorithm is proposed based on Eqs. (1-7).
1.2 Particle filterParticle filters are sequential Monte Carlo (MC) methods based on particle representation of probability densities[12]. As a type of powerful tool for dealing with the nonlinear and non-Gaussian problems, PF has been widely used in various fields, such as signal processing[13], target tracking[14], robotics[15], and image processing[16]. There are three phases of particle filter: generation of new particles, update of particles, and computation of particle weights.
In this section, to briefly review the generic PF and analyze the resampling algorithm, the Eqs. (1-7) are simplified as
| $ {{\mathit{\boldsymbol{X}}_k} = {f_{k - 1}}({\mathit{\boldsymbol{X}}_{k - 1}},{\mathit{\boldsymbol{V}}_{k - 1}}),} $ | (8) |
| $ {{\mathit{\boldsymbol{Z}}_k} = {h_k}({\mathit{\boldsymbol{X}}_k},{\mathit{\boldsymbol{W}}_k}),} $ | (9) |
where Xk∈
The general PF usually brings the problem of sample degeneracy which reduces estimation accuracy. So, the resampling algorithm is needed to deal with the degeneracy problem of general PF. It is the core of traditional resampling procedure that modifies the weighted approximate density f(x) to an unweighted density
| $ f(x) = \sum\limits_{i = 1}^N {{w_i}} \delta (x - {\chi _i}) $ | (10) |
is replaced by
| $ \hat f(x) = \sum\limits_{i = 1}^N {{{\hat w}_i}} \delta (x - {\chi _i}) = \sum\limits_{i = 1}^N {\frac{{{n_i}}}{N}} \delta (x - {\chi _i}), $ | (11) |
where ni is the number of copies of particle χi in the new set of particles {xk*}; wi,
| $ \mathop {{\rm{lim}}}\limits_{N \to \infty } E[{(\int g (x)f(x){\rm{d}}x - \int g (x)\hat f(x){\rm{d}}x)^2}] = 0. $ | (12) |
The core of different traditional resampling algorithms is determined by the method which is used to generate the xk*.
As mentioned above, four traditional resampling algorithms do not address the contradiction between improvement of estimation accuracy and maintaining the diversity of particles. In order to overcome these defects in the above resampling algorithms, a new resampling algorithm is proposed in the next section.
2 The proposal methodologyIn this section, a new resampling algorithm is introduced. Then an improved particle filter is proposed based on this resampling algorithm.
2.1 A new optimal algorithm based on reinforcement learning (RL)The proposed resampling algorithm is designed based on a new optimal algorithm. The optimal algorithm can be vividly called book-stack optimal algorithm (BOA). It is assumed there is a stack of books marked with X on the desk, and one of them is marked with xi. The book-stack can be described as
| $ \mathit{\boldsymbol{X}} = {[{x_1},{x_2}, \cdots ,{x_i}]^{\rm{T}}},i = 1,2, \cdots ,N. $ | (13) |
It is assumed that frequency of use, which is marked with wi, is different. A set of wi can be described as
| $ {\mathit{\boldsymbol{W}} = {{[{w_1},{w_2}, \cdots ,{w_i}]}^{\rm{T}}},i = 1,2, \cdots ,N,} $ | (14) |
| $ {\sum\limits_{i = 1}^N {{w_i}} = 1.} $ | (15) |
Now extract a book every time according to the set of wi. Then wi of this book can be updated by Eq. (16).
| $ {w_i^* = p(w(i),i),i = 1,2, \cdots ,N,} $ | (16) |
where function p(·) is called update function of wi. An important property of p(·) is described as
| $ {p(x) > x,} $ | (17) |
where 0 < x < 1, x∈R.
Then the book extracted is placed on the top of book-stack. After many extractions, these books whose frequencies of use are higher will be on the top of book-stack, that is to say, the book whose frequency of use is higher obtains higher wi. The process of BOA can be vividly described in Fig. 2.

|
Download:
|
|
Fig. 2 The process of BOA |
|
Here, the action of RL is random sampling according to probability. The reward of RL is update of w. The state of RL is the state of X. So, the RL model of BOA can be described in Fig. 3.

|
Download:
|
|
Fig. 3 The model of BOA based on RL |
|
Similarly, particles of PF can be considered as books in book-stack. The weight of every particle can be looked upon as frequency of use for every book. So, a new resampling algorithm is proposed based on BOA, and it is called book-stack optimal resampling (BOR). It hardly brings the problem of particle impoverishment and controls the extent of particle degeneration by adjusting p(·).
Proposition 2.1 The resampling algorithm BOR is convergent.
Proof For simplicity, the particles of particle set X=[x1, x2, …, xn]T are arranged in the order of the weight of normalization, i.e., in the set of weight W=[w1, w2, …, wn]T,
| $ {{w_i} > {w_j},i > j.} $ | (18) |
The set of particles
| $ {{{\hat w}_i} > {{\hat w}_j},i > j.} $ | (19) |
According to Bernoulli's law of large numbers,
| $ {\mathop {{\rm{lim}}}\limits_{n \to \infty } P(\left| {\frac{{{n_i}}}{N} - {w_i}} \right| < \varepsilon ) = 1,} $ | (20) |
where ni is the number of times the xi is extracted after taking N samples. The wi is the weight of xi.
According to the property of p(·), i.e.,
| $ {p(x) > x,x \in R,} $ | (21) |
the order of particles in particle set is constant when N→∞, that is to say,
| $ {{x_i} = {{\hat x}_i},i = 1,2,3, \cdots ,N.} $ | (22) |
Here, p(·) can be assumed as
| $ {p({w_i},i) = a \cdot w(i),} $ | (23) |
where a>1, a∈R. The new weight
| $ \begin{array}{*{20}{l}} {{{\hat w}_i} = \frac{{p({w_i})}}{{p({w_1}) + p({w_2}) + \cdots p({w_N})}}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{{a \cdot {w_i}}}{{a \cdot {w_1} + a \cdot {w_2} + \cdots a \cdot {w_N}}}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{{{w_i}}}{{{w_1} + {w_2} + \cdots {w_N}}} = {w_i}.} \end{array} $ | (24) |
Further,
| $ \begin{array}{*{20}{l}} {E{{\left[ {(\int {f(x)} g(x){\rm{d}}x - \int {f(x)} \hat g(x){\rm{d}}x)} \right]}^2}}\\ { = \mathop {{\rm{lim}}}\limits_{N \to \infty } E[{{(\sum\limits_{i = 1}^N {{x_i}} {w_i} - \sum\limits_{i = 1}^N {{{\hat x}_i}} {{\hat w}_i})}^2}] = 0.} \end{array} $ | (25) |
To sum up, the probability distribution function (PDF) after resampling by BOR is close to the origin PDF when N→∞. So, the resampling algorithm BOR is convergent.
2.3 The improved PFAn improved PF which is called BPF is designed based on BOR. The BPF includes two parts which are general PF and BOR. To introduce BPF, the model used has been defined in Eq. (8) and Eq. (9). According to the state space model used, the statistical model of the system can be defined as
| $ p({X_0}),p({X_k}|{X_{k - 1}}),p({Z_k}|{X_k}). $ |
The p(X0) is the initial distribution and is known previously. The p(Xk|Xk-1) is the transition distribution according to Eq. (8). The p(Zk|Xk) is the observation equation corresponding to Eq. (9). In general, the assumptions are also made for the system that Xk subjects to the first-order Markov process and Zk is conditionally independent of the given Xk[18]. Z0k={Z1, Z2, …, Zk} and X0k={X1, X2, …, Xk} are used to denote the sequences of states and observations. As we know, the estimation of state can be approximated according to general PF as
| $ {\chi _k^i\backsim q[{\mathit{\boldsymbol{X}}_k}/(\mathit{\boldsymbol{X}}_0^{k - 1},Z_0^k)](i = 1,2,3, \cdots ,N),} $ | (26) |
| $ {{w_k} = {w_{k - 1}}\frac{{p({\mathit{\boldsymbol{X}}_k}/\mathit{\boldsymbol{X}}_0^{k - 1})p({\mathit{\boldsymbol{Z}}_k}/{\mathit{\boldsymbol{X}}_k})}}{{q[{\mathit{\boldsymbol{X}}_k}/(\mathit{\boldsymbol{X}}_0^{k - 1},\mathit{\boldsymbol{Z}}_0^k)]}},} $ | (27) |
| $ {\tilde w_k^{(i)} = \frac{{w_k^i}}{{\sum\nolimits_{j = 1}^N {w_k^j} }},} $ | (28) |
| $ {{{\tilde X}_k} = \sum\limits_{i = 1}^N {\chi _k^i} \tilde w_k^i,} $ | (29) |
where χ0i(i=1, 2, 3, …, N) is the initial particle, N is the number of particles, q[Xk/(X0k-1, Z0k)] is proposal distribution, χki is the particle generated according to q[Xk/(X0k-1, Z0k)],
The particle set and weights are calculated by using Eq. (27) and Eq. (28). The BOR resampling algorithm is used to deal with the particle set and weights in BPF. To describe how to apply BOR and show the main frame of BPF, the pseudocode of BPF based on MATLAB is described in Algorithm 1.
|
Algorithm 1 BPF algorithm Input: initial state, X0; initial weight, W0; initial covariance matrix, P; process noise covariance matrix, Q; observation noise covariance matrix, R; number of particles, N; process model, ProcessEq(·); observation model, ObservationEq(·); Output: the estimation of state, For k←1 to T do For i←1 to T do χi~q[Xk/(X0k-1, Z0k)], ParticleSet(i)=χi; End For i←1 to T do End Wk=Wk./sum(Wk); [Wk, ParticleSet]=BOR(Wk, N, ParticleSet); For i←1 to T do End End Function ObservationEq (Xk) Zk=ObservationEq(Xk); Return Zk; Function ProcessEq (Xk-1) Xk=ProcessEq(Xk-1); Return Xk; Function BOR (Wk, N, ParticleSet) OriginIndex=1: N, Bookcase=Xparticles; SampleIndex~sample (N, weight); %Sample according to weight, record their index. Bookcase=Xparticles; For i < N For j < N If SampleIndex (i)==OriginIndex(j) Then IndexPick=OriginIndex(j); OriginIndex(j)=NULL; OriginIndex=[IndexPick, OriginIndex]; Wk(j)=CostFunction(Wk(j)); %Update the weight; particleSample=Bookcase(j); Bookcase(j)=NULL; Bookcase=[particleSample, Bookcase]; Break; End End End Wk=Wk(:, OriginIndex); Wk=Wk./sum(Wk); ParticleSet=Bookcase; Return ParticleSet, Wk Function CostFunction (weight, int a) weight=weight*a; Return weight; |
In previous sections, a new resampling algorithm called BOR and an improved PF based on BOR are proposed for underwater mining navigation. To assess the performance of the proposed methods, the approaches will be tested and compared with field test data from Qiandao Lake. Qiandao Lake, a man-made lake located in Zhejiang, China, is a suitable place for underwater experiment. The lake covers an area of 573 km2 and has a storage capacity of 17.8 km3. It is clear and calm. The vehicle used is a human occupied vehicle (HOV) called Shenhaiyongshi. Its features and sensors are detailed in Table 1 and Table 2.
|
|
Table 1 Features of Shenhaiyongshi |
|
|
Table 2 Navigation sensors |
The signals of LBL, DVL, and FOG from Shenhaiyongshi are used to compose the observation vector Zk in Eq. (7). The signals of LBL are taken as north position x and east position y in Zk. The signals of DVL are used as forward velocity u and starboard velocity v in Zk. The heading angle ϕ and angular velocity α in Zk are from the signals of FOG.
3.1 Comparison between BOR and SIRTo assess the performance of BOR, comparison between the PF based on BOR and the PF based on SIR is designed. The settings of the two filters should be the same:
| $ \begin{array}{l} \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{x}}_0} = {{[0,0,3.2962,1.19,0]}^{\rm{T}}},}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{P}}_0} = {\rm{diag}}\{ 0.5,0.5,5 \times {{10}^{ - 3}},5 \times {{10}^{ - 3}},5 \times }\\ {{{10}^{ - 5}}\} ,} \end{array}\\ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{P}} = {\rm{diag}} \{ 5 \times {{10}^{ - 3}},0.3,0.3,5 \times {{10}^{ - 5}}\} ,}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{Q}} = {\rm{diag}} \{ 5 \times {{10}^{ - 3}},5 \times {{10}^{ - 3}},5 \times {{10}^{ - 3}},5}\\ {{{10}^{ - 3}},5 \times {{10}^{ - 5}}\} ,}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} N = 10,} \end{array} \end{array} $ |
where x0 is the initial state, P0 is the initial covariance matrix, P is the process noise covariance matrix and Q is the observation noise covariance matrix. Additionally, the update function p(·) can be defined as
| $ p(i) = w(i) \times 4. $ | (30) |
To simulate the mining environment of high noise, Gamma noise is added to observation signal of LBL. The gamma noise is generated by
| $ {\rm{Ngamma}} = a \times {\rm{ gamrnd}} (m,n,p,q) $ | (31) |
where a>0∈
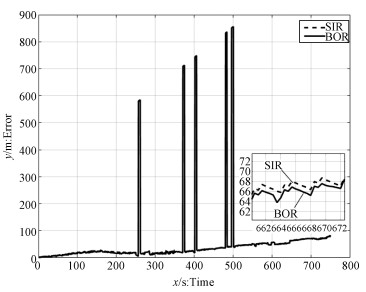
In Fig. 4, it is shown that two resampling algorithms have good estimation accuracy. However, the track of BOR is closer to the track of LBL. In Fig. 5 it is shown the difference of estimation accuracy between BOR and SIR. To further detail the errors of estimation, the mean absolute error (MAE) and standard deviation (SD) are introduced. They are displayed in Table 3.

|
Download:
|
|
Fig. 4 Results of the two resampling algorithms |
|
|
Download:
|
|
Fig. 5 Errors of the two resampling algorithms |
|
|
|
Table 3 The MAE and SD of SIR and BOR |
It is seen in Fig. 5 and Table 3 that the PF based on BOR has smaller estimation errors than that based on SIR. We analyze the positioning error data of the simulation period in Fig. 5, and the PF based on SIR has more evident errors with time because the extent of particle impoverishment gradually increases. In this period, the accuracy of position rises by 4.88% according to Table 3. Therefore, BOR algorithm has more accurate estimation and alleviates particle impoverishment by changing weight of particles instead of multiplying particles.
3.2 Contrast between UKF and BPFTo evaluate the performance of underwater mining system based on BPF, the simulation comparing the results of UKF and BPF is designed. Similarly, the setting of two filters should be the same:
| $ \begin{array}{l} \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{x}}_0} = {{[0,0,3.2962,1.19,0]}^{\rm{T}}},}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{P}}_0} = {\rm{diag}}\{ 0.5,0.5,5 \times {{10}^{ - 3}},5 \times {{10}^{ - 3}},5 \times }\\ {{{10}^{ - 5}}\} ,} \end{array}\\ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{P}} = {\rm{diag}} \{ 5 \times {{10}^{ - 3}},0.3,0.3,5 \times {{10}^{ - 5}}\} ,}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{Q}} = {\rm{diag}} \{ 5 \times {{10}^{ - 3}},5 \times {{10}^{ - 3}},5 \times {{10}^{ - 3}},5}\\ {{{10}^{ - 3}},5 \times {{10}^{ - 5}}\} ,}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} N = 100,} \end{array} \end{array} $ |
where x0 is the initial state, P0 is the initial covariance matrix, P is the process noise covariance matrix and Q is the observation noise covariance matrix.
The update function p(·) can be defined as
| $ p(i) = w(i) \times 4. $ | (32) |
To simulate the mining environment of high noise, gamma noise is added to observation signal of LBL. The gamma noise is generated by Eq. (31).
When a=10 in Eq. (31), the fusion results and position error of UKF and BPF are shown in Figs. 6 and 7. The track of BPF is smoother than that of UKF and it is closer to the track of LBL, as shown in Figs. 6 and 7. It is seen that the BPF has more credible navigation than the UKF. Furthermore, the BPF generates an ideal track when the signal of LBL is deficient in Fig. 7(a), i.e., the BPF has prominent robustness.

|
Download:
|
|
Fig. 6 Different position results of UKF and BPF |
|

|
Download:
|
|
Fig. 7 Results and errors of UKF and BPF |
|
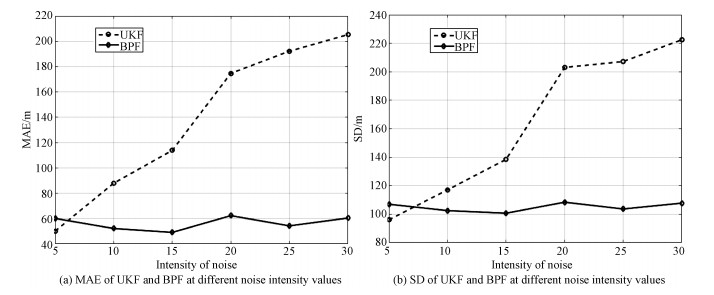
To reveal the advantage of BPF deeply, MAE and SD at different intensity values of noise are introduced to evaluate the estimation results of UKF and BPF, as illustrated in Fig. 8. As shown in Fig. 8, when a=5 in Eq. (31), the errors of UKF is smaller than those of BPF because the number of particles is little. However, the errors of UKF increase rapidly with the increase of noise intensity and the errors of BPF change little. It is seen that the BPF has the ability to eliminate the influence of noise.
|
Download:
|
|
Fig. 8 Results of UKF and BPF at different noise intensity values |
|
In this study, we have presented a new resampling algorithm called BOR as an improvement to the PF. By adjusting weight of particles instead of multiplying particles, the proposed BOR algorithm overcomes the defects of the traditional resampling algorithm and solves the problems of particle degeneracy and impoverishment simultaneously. Simulations show that the BOR algorithm improves the accuracy of estimation and maintains the diversity of particles.
To address the problems of non-Gaussian and intense noise in underwater mining navigation, an improved PF based on BOR is proposed. Simulations indicate that the BPF gives very brilliant performance of estimation and the accuracy of BPF is higher than that of UKF. Further, the robustness of BPF is prominent.
| [1] |
Yeu T K, Yoon S M, Park S J, et al. Study on underwater navigation of crawler type mining robot[C]//OCEANS 2011. IEEE, 2011: 1-6.
|
| [2] |
Pratama, P S, Kim J W, Kim H K, et al. Path planning algorithm to minimize an overlapped path and turning number for an underwater mining robot[C]//15th International Conference on Control, Automation and Systems (ICCAS). Busan, Korea (South): IEEE, 2015: 499-504.
|
| [3] |
Leonard J J, Bahr A. Autonomous underwater vehicle navigation[M]. Springer Handbook of Ocean Engineering. Springer International Publishing, 2016: 663-678.
|
| [4] |
Liu B, Liu K Z, Wang Y Y, et al. A hybrid deep sea navigation system of LBL/DR integration based on UKF and PSO-SVM[J]. Robot, 2015, 37(5): 614-620. |
| [5] |
Wang S, Gui W, Chen D. Date fusion of orientation of deep-seabed mining vehicle[J]. Journal of Central South University, 2011, 42(3): 337-340. |
| [6] |
Doucet A, Godsill S, Andrieu C. On sequential Monte Carlo sampling methods for Bayesian filtering[J]. Statistics and computing, 2000, 10(3): 197-208. |
| [7] |
Carpenter J, Clifford P, Fearnhead P. Improved particle filter for nonlinear problems[J]. IEE Proceedings-Radar, Sonar and Navigation, 1999, 146(1): 2-7. DOI:10.1049/ip-rsn:19990255 |
| [8] |
Yin S, Zhu X, Qiu J, et al. State estimation in nonlinear system using sequential evolutionary filter[J]. IEEE Transactions on Industrial Electronics, 2016, 63(6): 3786-3794. DOI:10.1109/TIE.2016.2522382 |
| [9] |
Chen N, Ji H, Gao Y, et al. New box particle filter with improved resampling method and extended inclusion volume criteria for multi-target tracking[J]. Radioengineering, 2018, 27(3): 847. |
| [10] |
Jouin M, Gouriveau R, Hissel D, et al. Particle filter-based prognostics:review, discussion and perspectives[J]. Mechanical Systems and Signal Processing, 2016, 72: 2-31. |
| [11] |
Li T, Bolic M, Djuric P M. Resampling methods for particle filtering:classification, implementation, and strategies[J]. IEEE Signal Processing Magazine, 2015, 32(3): 70-86. DOI:10.1109/MSP.2014.2330626 |
| [12] |
Li T, Villarrubia G, Sun S, et al. Resampling methods for particle filtering:identical distribution, a new method, and comparable study[J]. Frontiers of Information Technology & Electronic Engineering, 2015, 16(11): 969-984. |
| [13] |
Read J, Achutegui K, Míguez J. A distributed particle filter for nonlinear tracking in wireless sensor networks[J]. Signal Processing, 2014, 98: 121-134. DOI:10.1016/j.sigpro.2013.11.020 |
| [14] |
Li J, Zhao R, Chen J, et al. Target tracking algorithm based on adaptive strong tracking particle filter[J]. IET Science, Measurement & Technology, 2016, 10(7): 704-710. |
| [15] |
Wu B F, Jen C L. Particle-filter-based radio localization for mobile robots in the environments with low-density WLAN APs[J]. IEEE Trans Industrial Electronics, 2014, 61(12): 6860-6870. DOI:10.1109/TIE.2014.2327553 |
| [16] |
Sonka M, Hlavac V, Boyle R. Image processing, analysis, and machine vision[M]. 4th ed. New York: Springer, 2011.
|
| [17] |
Chang W, Chen C, Jian Y. Visual tracking in high-dimensional state space by appearance-guided particle filtering[J]. IEEE Transactions on Image Processing, 2008, 17(7): 1154-1167. DOI:10.1109/TIP.2008.924283 |
| [18] |
Yin S, Zhu X. Intelligent particle filter and its application to fault detection of nonlinear system[J]. IEEE Transactions on Industrial Electronics, 2015, 62(6): 3852-3861. |
 2020, Vol. 37
2020, Vol. 37 


