2. 中国科学院大学, 北京 100049;
3. 中国科学院微小卫星创新研究院, 上海 201203
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Institute of Microsatellite Innovation, Chinese Academy of Sciences, Shanghai 201203, China
频谱资源是无线通信中一种有限而珍贵的自然资源,通常由国家管理并分配给各大无线通信系统[1]。随着无线设备和无线服务的不断增长,有限的频谱资源被不断占用[2],固定的频谱分配策略已经不能适应无线网络日益增长的需求[3]。卫星、蜂窝等各种无线通信网络在建设前都需要进行手续复杂的频率申请过程,这些过程给日益追求快速建设的无线网络的研制周期、投入市场周期及其产生的经济效益带来了巨大的压力。
ISM(industrial scientific medical)频段由国际电联无线电通信组织定义,属于免授权通信频段,无线设备只需要满足发射功率和天线增益等方面的要求即可自由使用该频段。得益于该频段使用的自由度,近年来,Wi-Fi、蓝牙、ZigBee等无线协议得到广泛应用,无线局域网、智能家居等相关产品取得了空前的经济效益。因此,星地、空地、蜂窝[4]等传统的需要申请专用频段的无线通信系统也开始论证在ISM频段下工作的可行性。尤其是当前ISM频段设备以室内应用为主,这为在室外进行ISM频段下的星地、空地、蜂窝等通信提供了相对空闲的频谱环境。
ISM频段工作的无线设备需要遵循载波监听/冲突避免算法(CSMA/CA, carrier sense multiple access/collision avoidance)[5],从而实现频谱资源的共享,如何保证频谱资源的可靠性成为在该频段进行星地等通信的关键问题。
随着认知无线电的发展[6],文献[7]提出一种针对ISM频段的信道抑制探测算法,通过感知分析对多个目标信道进行探测,从而找寻合适的通信信道以达到避免干扰的目的。文献[8]从Wi-Fi协议层出发,提出一种在ISM频段下的抗干扰方案,为通信系统在ISM频段实现可靠通信提供了技术基础。该方案利用ISM频段设备需要遵循CSMA/CA算法的特点,通过广播信道占用控制帧(CTS, clear to send),使接收到广播信号的设备执行冲突避免算法,从而维持信道的空闲状态,实现净空效果。净空技术通过周期性发送伪装的资源声明信号,实现通信资源的周期性占用。
然而,上述净空技术实现时所发送的净空信号将对目标系统的信号接收带来严重的自干扰问题:1)在发送净空的时隙,净空信号将淹没接收信号,甚至造成接收链路器件饱和;2)在不发送净空的时隙,净空链路将抬升接收链路的底噪,影响接收机灵敏度。因此,净空技术和收发信机的一体化设计是在ISM频段下采用资源占用方式进行星地、空地、蜂窝等通信的关键技术问题,目前尚无文献及相关研究解决该问题。
本文设计一种基于净空技术的ISM频段可靠无线通信系统,为了提高系统隐蔽性、抗干扰能力以及多址能力,采用扩频通信体制。传统的扩频通信抗干扰手段主要有:1)频域抗干扰;2)空域抗干扰[9];3)空时抗干扰[10]。其中,频域抗干扰对干扰成分进行零陷处理或者采用自适应滤波器技术[11],缺点是无法对宽带干扰做有效处理。空域抗干扰利用相控阵天线的波束形成技术,在干扰方向形成零陷[12],且通过增加微分约束条件,提高动态干扰下的稳健性[13]。空时抗干扰采用天线阵列,利用信号特征完成干扰抵消,是将空/频域抗干扰由一维推广到二维的结果。以上抗干扰手段主要面向窄带干扰,而基于净空技术的ISM频段通信系统存在的是远高于本身通信带宽的宽带短时强干扰,通过扩频本身以及传统的抗干扰手段都难以解决。
面向上述问题,本文针对净空技术和收发信机的一体化设计进行相关研究。针对ISM频段抗干扰的原理及信道占用帧的特点,建立系统模型和时序模型。通过对信道占用帧自干扰问题的分析,从系统复杂度和通信质量的权衡角度提出AD清零和基站盲发模式。对于清零可能带来的系统影响,分别从理论误码率、捕获、跟踪的角度进行仿真验证。在硬件设计方面,通过对接收机模块的底噪分析并结合信道占用帧的周期性特点,提出在净空发射模块添加射频开关增大收发隔离度并根据信道占用帧周期对其进行控制的设计。最后,对ISM频段无线通信系统进行实测,结果证明了在ISM频段进行星地等专用通信系统软硬件设计的可行性。
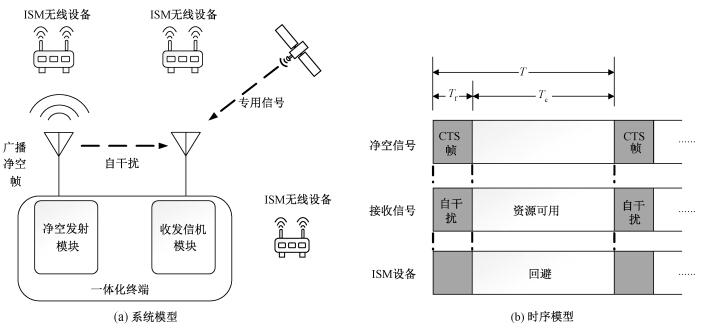
1 模型方案介绍作为免授权的共享频段,ISM频段工作有大量的无线设备,在这个有限的时频资源内,各设备之间相互竞争。为了避免竞争过程中的相互干扰,各设备遵循CSMA/CA算法,即接入前需对信道忙碌状态进行监听。IEEE 802.11协议规定ISM设备需根据信道中传输的信号在介质访问控制层(MAC, media access control)的网络分配矢量(NAV, network allocation vector)中声明的信道占用时间来同步更新设备本身该字段的数值,实现当前设备信道接入前的合理退避。
图 1(a)中一体化终端利用该协议,通过净空发射模块发送信道占用控制帧(CTS帧)对信道进行声明占用。在一个CTS帧声明占用时间结束前,发送下一个CTS帧,通过周期性地发送占用帧实现周期性的频谱资源占用,为终端收发模块在该伪装占用的信道中实现专用通信提供保障。ISM频段下的无线通信系统模型包括一体化终端、远端基站(收发专用信号)和ISM频段其他无线设备。其中,一体化终端由净空发射模块(广播净空信号)和收发信机模块(实现专用通信)组成。
|
Download:
|
| 图 1 系统模型 Fig. 1 System model | |
如图 1(b), 系统的通信时序模型包括净空信号时序、接收信号时序和ISM设备时序。其中, 净空信号时序由净空发射模块控制, 其在Tf时间内发送CTS帧(净空帧), Tc时间内不发送信号, 周期时间为T(T=Tf+Tc)。接收信号时序对应收发信机模块时序, 由于专用信号的收发采用频分双工模式, 仅接收链路工作在伪装信道, 故本文只考虑接收情况。在Tf时间内, 接收机接收专用信号, 同时受到净空发射模块的净空帧自干扰影响; 在Tc时间内信道资源可用, 不受净空帧影响。ISM设备根据CSMA/CA算法, 持续监听信道中的净空信号并在相应时间内回避。
2 系统设计及性能分析 2.1 射频AD清零策略为保证信道占用的可靠性,净空帧的发射功率需要满足一定要求,实际应用中应尽可能地提高发射功率。ISM频段规定设备的最大发射功率为1 W[14],然而,以星地通信为例,地面接收机天线入口信号电平低至-130 dBm,与净空帧的最大功率相差近160 dB。如果忽略净空帧自干扰的影响,在该信道环境下进行专用通信,接收机相干积分的结果必然受到极大影响,捕获跟踪过程难以保障,系统误码率恶化。为了避免Tf时间内的净空自干扰影响,可以在净空发送的间隙(Tc时间内)完成专用通信,但这引入了终端和基站的时钟同步问题。星地、空地等远距离通信过程中握手和反馈将带来时效性损失且增加了系统复杂度。
本文采用对接收机Tf时间内射频AD芯片数据擦除并填充固定电平的处理。由于Tf时长相对于伪码周期和信息时长较短,系统误码率将受到Tf时段对应的接收机本地伪码特性和填充电平的影响。经过大量仿真并考虑系统实现的简单性,最终采用AD清零和基站盲发策略。
基站盲发是指基站在整个通信过程中持续发送专用信号,并不考虑净空帧发送时隙。AD清零是指由于净空自干扰是带有先验时间信息的系统自发干扰,接收机对射频AD芯片Tf时间内的数据进行清零,Tc时间内的数据保持不变。硬件实现时,考虑接收与发送的先入选出(FIFO,first input first output)延时以及射频链路延时后,对接收机AD芯片Tf时段的FIFO数据进行清零。
2.2 清零策略的理论误码率通过对AD芯片Tf时间内的数据清零,接收机避免了Tf时间内净空帧自干扰的影响,同时带来了Tf时间内有用信号的损失以及部分热噪声的去除。其中,有用信号功率衰减因子为
| $ {\rm{deg}} ({\rm{ signal }}) = {(1 - Bdc)^2}, $ | (1) |
热噪声功率衰减因子为
| $ {\rm{deg}} (\begin{array}{*{20}{l}} {{\rm{thermalnoise}}} \end{array}) = (1 - Bdc), $ | (2) |
式中,Bdc为清零数据占总数据量的比值,即
| $ Bdc = {T_{\rm{f}}}/T = {T_{\rm{f}}}/({T_{\rm{f}}} + {T_{\rm{c}}}). $ | (3) |
定义采用AD清零策略后的等效载噪比为
| $ C/{N_{{\rm{0, EFF}}}} = \frac{{C \times {{(1 - Bdc)}^2}}}{{{N_0} \times (1 - Bdc)}} = \frac{C}{{{N_0}}} \times (1 - Bdc), $ | (4) |
转化为对数形式
| $ {[C/{N_{{\rm{0, EFF}}}}]_{{\rm{dB}}}} = {\left[ {\frac{C}{{{N_0}}}} \right]_{{\rm{dB}}}} + 10{\rm{lg}}(1 - Bdc), $ | (5) |
式中:C为有用信号载波功率,N0, EFF为有效噪声密度,N0为热噪声功率谱密度。式(5)表明AD清零对比无干扰情况带来了10lg(1-Bdc)的载噪比损失。
AD清零策略带来的载噪比损失与清零数据量占比有关。占比越小,信噪比损失越少。CTS帧是持续时间最短的控制帧,可以最大程度地避免损失。同时,由于信噪比与误码率有关,根据清零数据占比可以推导系统理论误码率。
设专用信号采用CDMA体制,调制采用BPSK方式,则专用信号可表示为
| $ \begin{array}{*{20}{c}} {s(t) = Ax(t - \tau )D(t - \tau ){\rm{sin}}(2\pi (f + }\\ {{f_{\rm{d}}})(t - \tau ) + \theta ), } \end{array} $ | (6) |
式中:A为信号振幅;x(t)为扩频码,D(t)为数据码,x(t), D(t)∈{+1, -1};f为载波频率;fd为多普勒频移;τ为传播延时;θ为初相位。假设载波环与码环正常工作,s(t)中扩频码与载波成功剥离,系统误码率转换为BPSK理论误码率。设双极性码基带系统的有用信号幅度大小为A,信道噪声为高斯白噪声,经低通滤波器后为高斯带限噪声nR(t),其瞬时值V的一维概率密度为
| $ f(V) = \frac{1}{{\sqrt {2\pi } {\sigma _n}}}{{\rm{e}}^{ - {V^2}/2\sigma _n^2}}, $ | (7) |
则发送“0”“1”时的判决信号分别为-A+nR(t),A+nR(t),系统总误码率定义为
| $ {p_{\rm{e}}} = p(0)p(1/0) + p(1)p(0/1). $ | (8) |
式中:p(0/1)为发送“1”错判“0”的条件概率,p(1/0)为发送“0”错判“1”的条件概率,p(0)为发送“0”的概率,p(1)为发送“1”的概率。设Vd为判决门限,当
| $ {p_{\rm{e}}} = \frac{1}{2} erfc \left( {\frac{A}{{\sqrt 2 {\sigma _n}}}} \right). $ | (9) |
对于持续时间Tb,载波幅度A的BPSK调制信号,比特能量
| $ {p_{\rm{e}}} = \frac{1}{2} erfc \left( {\sqrt {\frac{{{E_{\rm{b}}}}}{{{N_0}}}} } \right). $ | (10) |
由式(5)可知,AD清零带来的载噪比损失以dB为单位为
| $ {\left[ {\Delta \frac{C}{{{N_0}}}} \right]_{{\rm{dB}}}} = 10{\rm{lg}}(1 - Bdc), $ | (11) |
所以,AD清零策略下BPSK系统理论误码率为
| $ {p_{\rm{e}}} = \frac{1}{2} erfc\left( {\sqrt {\frac{{{E_{\rm{b}}}}}{{{N_0}}}(1 - Bdc)} } \right). $ | (12) |
由图 1(b)的时序模型可知,在净空发射模块不发送净空帧期间(Tc时间内),接收机可正常接收专用信号。虽然该时间内无净空帧自干扰,但是由于终端一体化的设计,净空发射模块的底部噪声将馈入接收机模块,从而造成接收机底部噪声抬升。对于星地通信这类敏感链路,底噪抬升将造成误码率恶化。通常情况下,接收机天线端口的底部噪声考虑为环境热噪声,其公式为
| $ {N_0} = 10{\rm{lg}}(K{T_0}), $ | (13) |
式中:K为波尔兹曼常数,K=1.38×10-23 J/K;T0为标准噪声温度;N0为热噪声功率谱密度,在常温T0=290 K时,求得标准值约为-174 dBm/Hz。在实际的工程应用中,底噪抬升带来信噪比的恶化,恶化0.1 dB时,这种恶化带来的误码率影响可以忽略不记,结合式(13)表示为
| $ 10{\rm{lg}}(K{T_0}) - 10{\rm{lg}}(K{T_0} + x) = 0.1, $ | (14) |
式中x(以J为单位)为净空发射模块馈入接收机链路的噪声功率谱密度,解式(14)可得
| $ 10{\rm{lg}}x = - 190, $ | (15) |
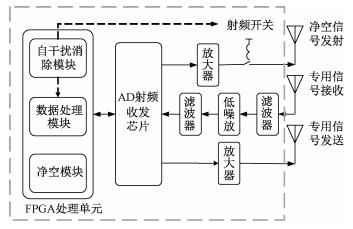
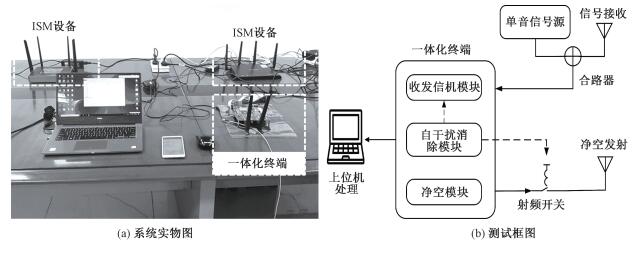
为保证信道占用的可靠性,净空发射模块需要搭载放大器从而提高净空帧发射功率。然而,由式(15)的计算结果可知,净空发射模块馈入的噪声功率谱密度理论上不能高于-190 dBm/Hz,所以净空发射模块与接收机模块之间需进行射频隔离。如图 2所示,硬件设计中采用CSWA2-63DR+射频开关,理想情况下隔离度可以达到44 dB。根据净空帧发送周期对其进行控制,在Tc时间内关断从而增大收发模块隔离度,在Tf时间内闭合从而保证净空帧正常发送。其具有ns级别的接通关断能力,远小于净空帧的持续时间Tf以及信道占用持续时间Tc。
|
Download:
|
| 图 2 硬件框图 Fig. 2 Hardware block diagram | |
图 2虚线框内为一体化终端设计,其中净空模块完成净空信号的产生,信号经过射频收发芯片发射端、放大器、射频开关和天线。数据处理模块完成专用信号的收发处理,待接收的专用信号经过天线、滤波器、低噪放、滤波器、射频收发芯片接收端,最终进入数据处理模块进行基带处理。待发送的专用信号由数据处理模块产生,经过射频收发芯片发射端、放大器和天线。自干扰消除模块完成对净空链路自干扰的消除,其工作包括:1)对Tf时间段数据处理模块的FIFO数据清零;2)控制射频开关的状态,保证Tf时间内闭合,Tc时间内断开。
3 仿真验证及实测 3.1 清零策略的误码率验证为了研究不同功率下净空帧自干扰对接收机误码率的影响,同时验证射频AD清零的可行性,对系统理论误码率进行仿真,仿真参数见表 1。
|
|
表 1 误码率仿真参数 Table 1 Simulation parameters of bit error rate |
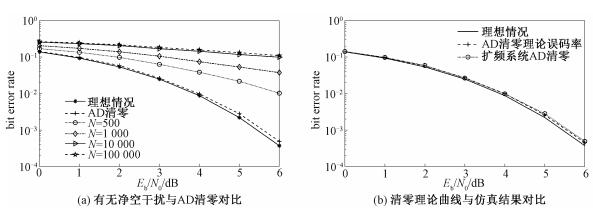
设置3种仿真条件:1)无净空帧自干扰,2)Tf时间内射频AD清零,3)存在幅值大小为N的净空帧自干扰,仿真结果如图 3(a)所示。由图 3(a)的对比结果可知,采用对Tf时间段AD信号清零的策略可以获得较低的误码率,当Eb/N0=6 dB时,误码率相较于理想情况的偏差在10-4数量级。如果忽略对净空帧自干扰的处理,解扩解调后的信号将受到恶化,误码率的恶化程度与自干扰的幅值有关。自干扰幅值越大,恶化越严重。系统中净空帧的功率远高于专用信号功率,所以设计中无法忽略净空帧自干扰的影响。同时,根据2.2节可知接收机采用AD清零会导致10lg(1-Bdc)的载噪比损失,图 3(b)根据损失量画出AD清零理论误码率曲线,并与实际扩频系统AD清零误码率仿真曲线对比,两条曲线基本吻合,证明了系统理论分析的正确性。
|
Download:
|
| 图 3 误码率曲线对比 Fig. 3 Comparison of bit error rate | |
捕获采用PMF-FFT算法,仿真参数见表 2,根据参数对不同情况的捕获仿真结果见图 4。
|
|
表 2 捕获仿真参数 Table 2 Simulation parameters of captured results |

|
Download:
|
| 图 4 捕获结果对比 Fig. 4 Comparison of captured results | |
图 4(a)为存在净空帧自干扰时的仿真结果,捕获二维结果的峰均比较小,干扰频率和干扰码相位的基底噪声较大,目标频点与码相位被淹没。由于净空帧干扰是带有先验时间信息的系统自发干扰,FPGA控制单元可以有选择性地对有效信号进行捕获。针对净空帧发送间隙(Tc时间内)的捕获结果如图 4(b)所示,根据仿真参数可知多普勒频率步进量Δf=fs/(XP)=769.23 Hz,捕获峰值对应坐标(14, 1),计算可得对应频率和码相位(10e3 Hz, 1 chip),与设置的目标值相符。根据PMF-FFT算法的相关理论可知,捕获检测概率Pd为
| $ {P_{\rm{d}}} = 1 - \mathop \prod \limits_{k = 1}^N [1 - Q(\sqrt {2X \times P \times {\rm{SN}}{{\rm{R}}_{{\rm{in}}}}} |G({f_{\rm{d}}}, k)|, t)], $ | (16) |
式中:G(fd, k)为部分匹配滤波器输出进行N点FFT后的第k点输出的归一化幅度响应,t为恒虚警下捕获门限的归一化结果。设虚警率Pfa=10-5,代入参数可得Pd为1。PMF-FFT捕获时间公式为
| $ T = \frac{{2 + (2 - {P_{\rm{d}}})(q - 1)(1 + k{P_{{\rm{fa}}}})}}{{2{P_{\rm{d}}}}}{\tau _{\rm{d}}}, $ | (17) |
式中:q为搜索码片单元数,τd为逗留时间。采用并行匹配滤波器可算得T=6.5 ms,满足Tc的时间要求。
3.3 跟踪环路的仿真验证对于大功率的短时周期性净空自干扰,敏感的跟踪环路易受到较大影响[15]。针对净空帧不同的处理方式,对跟踪环路进行仿真验证,设置条件分别为:1)无净空帧自干扰,2)存在大功率自干扰,3)对Tf时间内AD清零。多普勒变化设置为频率斜升形式,跟踪环路为先锁频环后三阶锁相环,锁相环参数见表 3,仿真结果见图 5。
|
|
表 3 跟踪仿真参数 Table 3 Simulation parameters of tracking loop |
|
Download:
|
| 图 5 跟踪环路的仿真结果 Fig. 5 Simulation results of tracking loop | |
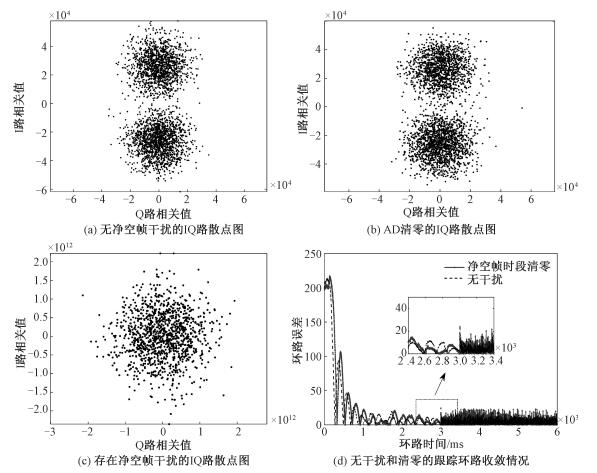
图 5(a)为无净空自干扰时接收机跟踪环路的IQ路积分散点图,图 5(b)为AD清零后的情况。可以发现AD清零的跟踪效果接近于无干扰情况,散点分布聚集,形成上下两个圆。图 5(c)为存在大功率净空自干扰的情况,由于净空帧干扰的功率远大于有用信号,IQ两路的积分结果明显增大多个数量级。同时由于净空帧信号相对于有用信号的随机性,相干积分后的IQ两路散点分布较为分散。根据锁相环跟踪门限相关理论可知
| $ 3{\sigma _{{\rm{PLL}}}} = 3{\sigma _i} + {\theta _{\rm{e}}} \le {45^\circ }, $ | (18) |
σPLL与C/N0有关,根据2.2节计算AD清零带来约0.1 dB的载噪比损失,相比正常几十量级的载噪比而言,对σPLL的影响忽略不计,式(18)的约束条件不受影响。图 5(d)为无净空帧自干扰和采用AD清零的环路输出收敛情况,两种情况下的环路跟踪效果接近,仿真结果同样证明了AD清零后环路跟踪稳定。
3.4 硬件自干扰消除的有效性实测系统硬件实物图如图 6(a)所示,终端控制单元为Xilinx公司的XC7Z100,它包括双核ARM Cortex-A9 MPCore处理器。射频AD芯片为AD9364,其工作频率范围为70 MHz~6.0 GHz,收发通道为1收1发。为了验证硬件自干扰消除的有效性,考察净空发射模块在射频开关断开期间对专用信号接收链路馈入的噪声影响,对硬件电路进行实测。测试原理框图如图 6(b),测试时刻分别为:1)无净空发射链路,2)净空帧发送间歇(Tc时间段)。测量数据由一体化终端送到上位机进行处理,处理结果如图 7所示。
|
Download:
|
| 图 6 系统实物图及测试框图 Fig. 6 System physical chart (a) and test block diagram (b) | |
|
Download:
|
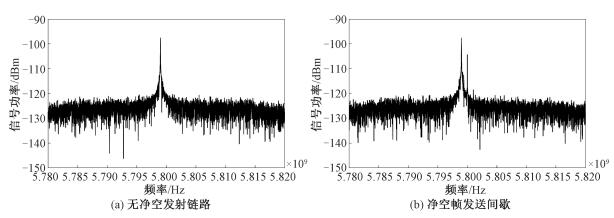
| 图 7 测试结果的频谱图 Fig. 7 Spectrum diagrams of test results | |
实测时,数据采样率fs=40 MHz,NFFT点数为4 096,频谱分辨率Δf=fs/NFFT≈10 kHz。图 7(a)为无净空发射链路,仅开启单音信号源时上位机对信号接收链路数据处理的频谱图,对底噪测量值取平均并考虑频谱分辨率10 kHz可得底噪约为-166.9 dBm/Hz。保持单音信号功率不变,图 7(b)为在净空链路发送间歇Tc时间段(射频开关断开时),信号接收链路的频谱图。对底噪测量值取平均并考虑频谱分辨率10 kHz可得底噪约为-166.8 dBm/Hz。对比图 7(a)和7(b)的底噪大小,可得结论:在净空帧发送间歇,净空发射模块对接收机模块馈入的底部噪声较小,底噪抬升约0.1 dB,与2.3节理论值相符,净空发射模块的设计以及隔离度满足系统要求。
3.5 ISM频段可靠无线通信系统实测系统总体测试过程包括以下3种情况:
1) 测试ISM设备未工作时的专用通信:①远端基站发送专用信号,②打开一体化终端接收通道。此时,上位机成功接收专用信号帧。
2) 测试周围ISM设备工作时的专用通信:①远端基站发送专用信号,②打开一体化终端接收通道,③打开路由器并等待启动,④连接电脑至路由器并发送文件。此时,电脑显示以Mb/s速率发送,而上位机无法接收专用信号帧。
3) 测试打开净空信号发射模块后的专用通信:①远端基站发送专用信号,②打开一体化终端接收通道,③打开路由器并等待启动,④连接电脑至路由器并发送文件,⑤打开净空发射模块。此时,电脑显示发送速率由Mb/s逐渐减小至0,无线网络断开,上位机再次成功接收专用信号帧。
通过以上3种情况下的实测,成功验证了在ISM频段实现一体化专用通信终端设计的可行性。系统误码率和信噪比的统计结果表明:相对于无ISM设备工作的理想情况,打开净空发射模块后专用通信系统信噪比实际恶化4 dB左右,该值在通信链路设计余量范围之内,系统具备实用性。
4 总结本文提出一种基于净空技术的ISM频段可靠无线通信系统软硬件方案。利用该方案可以实现共享频段下的星地、空地等专用通信,为专用通信系统建设节省了时间和金钱成本。该方案包括以下内容:首先,针对ISM频段抗干扰的原理及信道占用帧的特点,建立系统模型和时序模型。通过对一体化终端自干扰问题的分析,同时为了简化专用通信系统复杂度,提出专用信号盲发模式和AD清零策略。随后,对AD清零进行理论误码率验证。考虑到AD清零带来相干积分结果的损失从而影响捕获跟踪环路,针对捕获跟踪过程进行仿真验证。硬件设计上,通过对接收机底部噪声的分析,提出净空发射模块和接收机模块之间的隔离度要求以及根据净空帧周期控制射频开关的设计。随后,对硬件电路进行实测,通过对测试信号的频谱分析,验证硬件自干扰消除的有效性。最后,对一体化终端进行功能验证,通过对专用信号误码率和信噪比的统计,证明系统的实用性。
| [1] |
王钦辉, 叶保留, 田宇, 等. 认知无线电网络中频谱分配算法[J]. 电子学报, 2012, 40(1): 147-154. Doi:10.3969/j.issn.0372-2112.2012.01.024 |
| [2] |
Cai H, Huang K, Yuan W, et al. A propose of the iss space-to-space communication system by multiplexing ground mobile communication frequency resources[C]//Sixth International Conference on Instrumentation & Measurement. IEEE, 2016: 567-569.
|
| [3] |
Kumar K, Prakash A, Tripathi R. Spectrum handoff in cognitive radio networks:a classification and comprehensive survey[J]. Journal of Network & Computer Applications, 2016, 61(8): 161-188. |
| [4] |
王玮, 徐平平, 张源. 未授权频段LTE-LAA与WiFi共存系统性能分析[J]. 东南大学学报(自然科学版), 2017, 47(3): 426-431. |
| [5] |
Shenoy N, Hamilton J, Kwasinski A, et al. An improved IEEE 802.11 CSMA/CA medium access mechanism through the introduction of random short delays[C]//201513th International Symposium on Modeling and Optimization in Mobile, Ad Hoc, and Wireless Networks (WiOpt). IEEE, 2015: 331-338.
|
| [6] |
Tsiropoulos G I, Dobre O A, Ahmed M H, et al. Radio resource allocation techniques for efficient spectrum access in cognitive radio networks[J]. IEEE Communications Surveys & Tutorials, 2016, 18(1): 824-847. |
| [7] |
方思达. ISM频段频谱和干扰感知技术研究[D].北京: 北京邮电大学, 2018.
|
| [8] |
赵春丽. ISM频段认知无线电通信的抗干扰技术[D].北京: 北京邮电大学, 2018.
|
| [9] |
贾琼琼, 吴仁彪, 王文益, 等. 满足高精度测量的GNSS自适干扰抑制算法[J]. 电子学报, 2018, 46(11): 2753-2760. Doi:10.3969/j.issn.0372-2112.2018.11.024 |
| [10] |
杨琼, 张怡, 唐成凯. 基于凸优化的鲁棒GPS空时抗干扰算法[J]. 西北工业大学学报, 2016, 34(6): 1035-1039. Doi:10.3969/j.issn.1000-2758.2016.06.017 |
| [11] |
计茹.卫星导航系统频域-空域级联抗干扰算法及工程实现[D].西安: 西安电子科技大学, 2012.
|
| [12] |
李枫, 王紫阳, 王乐, 等. 抗干扰阵列天线的小型化及波束形成技术分析[J]. 西安电子科技大学学报, 2018, 45(6): 51-56. Doi:10.3969/j.issn.1001-2400.2018.06.009 |
| [13] |
Wang L, Han Y X. Moving jammer suppresion with robust blind adaptive algorithms in GPS receiver[J]. Journal of University of Chinese Academy of Sciences, 2015, 32(4): 556-561. |
| [14] |
Pelechrinis K, Broustis I, Krishnamurthy S V, et al. A measurement-driven anti-jamming system for 802.11 networks[J]. IEEE/ACM Transactions on Networking, 2011, 19(4): 1208-1222. Doi:10.1109/TNET.2011.2106139 |
| [15] |
Niamsuwan N, Johnson J T, Ellingson S W. Examination of a simple pulse-blanking technique for radio frequency interference mitigation[J]. Radio Science, 2016, 40(5): 1-11. |
 2020, Vol. 37
2020, Vol. 37 


