2. 北京航空航天大学物理科学与核能工程学院, 北京 10008
2. School of Physics, Beihang University, Beijing 100083, China
传统电子器件随着尺寸减小和集成密度增加,功耗和漏电问题愈发突出,已经触及“摩尔定律”能够达到的极限。因此,研究新型电子器件成为半导体工业的一项重要科学问题。不同于传统电子器件只利用电子的电荷自由度进行信息的处理与传输,自旋电子器件利用电子的电荷和自旋两个自由度对信息进行存储与处理,相较于传统的电子器件,具有速度快、功耗低、挥发性小、集成容量大等优点。
1988年, 巨磁电阻效应(giant magnetoresistance, GMR)[1-2]的提出,掀起自旋电子学的研究热潮。这个效应指出,在由铁磁层/非铁磁层/铁磁层构成的异质结材料中,铁磁层磁化方向平行时材料的电阻远小于反平行时电阻。具有高隧穿磁电阻(tunneling magnetoresistance, TMR)值的磁性隧道结(magnetic tunnel junction,MTJ)在非易失磁存储器件中有着非常重要的应用。文献[3]中,其定义为
| $ \text{TMR}=\left| \frac{{{I}_{\text{PC}}}-{{I}_{\text{APC}}}}{{{I}_{\text{APC}}}} \right|, $ |
式中:IPC和IAPC分别指当左右电极磁化方向平行(parallel configuration, PC)和反平行(antiparallel configuration,APC)时的电流值。在过去的许多年中,大量的理论预测和实验都致力于提高磁性隧道结的TMR值。在传统的磁性隧道结中,磁性金属一般是Fe,Co,Ni及其合金,绝缘体通常是Al2O3[4]和MgO[5-6]等金属氧化物。室温下首次探测到的TMR值是在CoFe-Al2O3-Co体系中测得的12%[7]。随后,相继在Fe-Al2O3-Fe体系中测得18%[4]的TMR值。近期,在磁性隧道结CoFeB-MgO-CoFeB中测得很大的TMR值[3],低温下高达1 100%,室温下也有600%。由实验测得的TMR值在逐渐提高。
在由磁性隧道结构成的自旋电子器件中,除TMR值,自旋注入效率(spin infection efficiency,SIE)也是一个很重要的性能指标。具有高SIE的磁性隧道结可以应用于自旋逻辑电路等[8], 所以寻求探索同时具有高TMR和高SIF的电子器件具有很重要的意义。Wolf等[9]在2001年指出,磁性半导体或者半金属可以作为自旋电子器件的候选材料。近年来,二维过渡金属卤族化合物成为继石墨烯[10],碳族、氮族[11-12]、过渡金属硫族化合物[13-16]之后的另一类热门二维材料,以其丰富卓越的物理性质,逐渐进入大家的视野,如其中通过第一性原理预测具有半金属性质的TiCl3、VCl3和ZrCl3[17]等材料,以及实验上成功剥落的RuCl3[18]和CrI3[19-20]层状薄膜等。
本文选取二维半金属TiCl3和半导体RhCl3分别作为自旋电子器件的电极和中心区搭建磁性隧道结,计算自旋极化相关输运性质。其中电极材料TiCl3通过第一性原理计算预测为半金属,呈铁磁性,居里温度约为376 K。且剥离能为0.33 J/m2[21],略小于石墨烯的剥离能0.36 J/m2[22],容易实现从块体到层状的剥离。在这样的半金属材料作为电极的自旋电子器件中,在小偏压范围内,TMR值一直保持稳定在100%。并且在电极材料磁化方向平行的情况下,磁性隧道结的SIE也保持在100%。即同时提高了器件的TMR和SIE。
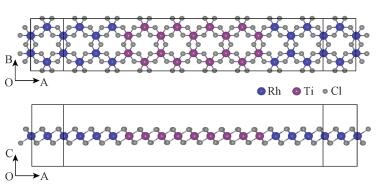
1 器件结构和计算方法在本文的研究中,由二维电极材料TiCl3和中心区RhCl3构成的平面异质结结构如图 1所示。为了模拟二维材料,层间取2 nm的真空层。TiCl3与RhCl3在AB平面内拼接,电流沿OA方向流动,整个体系在OB方向为周期性结构。为使两种材料晶体结构在OB方向匹配,将电极材料TiCl3沿OB方向压缩0.18%。计算表明,TiCl3在此应变下,其电子性质几乎没有变化。利用总能量弛豫的方法优化出最近邻的Ti原子和Rh原子之间的距离为0.604 nm。
|
Download:
|
| 图 1 器件的俯视图和侧视图 Fig. 1 The top view and side view of the device structure | |
本文的结构优化采用基于密度泛函理论的VASP软件包[23],广义梯度近似(generalized gradient approximation, GGA)的PBE[24]作为交换关联泛函,同时采用投影缀加平面波(projector augmented wave, PAW)方法构造赝势。结构优化计算中,平面波的截断动能选500 eV,总能量的收敛标准定为10-5 eV。量子输运性质的计算采用密度泛函理论和非平衡格林函数(non-equilibrium Green function,NEGF)方法相结合的Nanodcal软件包[25],其中价电子的轨道用DZP基组描述,原子核用模守恒赝势描述,采用LDA交换关联泛函。当所加偏压为V时,左(右)电极的化学势为μL=EF-eV/2(μR=EF+eV/2), 其中EF指费米能。依赖于自旋的电流可以表示为
| $ {{I}_{\sigma }}=\frac{\text{e}}{\text{h}}\int{{{T}_{\sigma }}(E, V)[{{f}_{\text{L}}}}(E, {{\mu }_{\text{L}}})-{{f}_{\text{R}}}(E, {{\mu }_{\text{R}}})]\text{d}E, $ | (1) |
式中:σ是代表自旋上下的指标,e、h和T分别指电子电荷、普朗克常量和透射系数。fL=(E, μL)和fR=(E, μR)分别是左右电极的费米分布函数。总电流为I=I↑+I↓。由不同偏压下的电流值,可以定义隧穿磁电阻(TMR)为
| $ \text{TMR}=\left| \frac{{{I}_{\text{PC}}}-{{I}_{\text{APC}}}}{{{I}_{\text{APC}}}+{{I}_{\text{APC}}}} \right|, $ | (2) |
式中:IPC和IAPC分别指当左右电极磁化方向平行和反平行时的电流值。本文关于TMR的计算均采用该定义,不同于一般文献中的定义。同时另外一个重要的物理量自旋注入效率SIE定义为
| $ \eta =\left| \frac{{{I}_{\uparrow }}-{{T}_{\downarrow }}}{{{I}_{\uparrow }}-{{T}_{\downarrow }}} \right|\times 100\%. $ | (3) |
当左右电极所加偏压为0时,用此时的透射系数代替电流值计算TMR值和SIE,即
| $ \text{TMR}=\left| \frac{{{I}_{\text{PC}}}-{{I}_{\text{APC}}}}{{{I}_{\text{APC}}}+{{I}_{\text{APC}}}} \right|, \eta =\left| \frac{{{I}_{\uparrow }}-{{T}_{\downarrow }}}{{{I}_{\uparrow }}-{{T}_{\downarrow }}} \right|\times 100\%. $ | (4) |
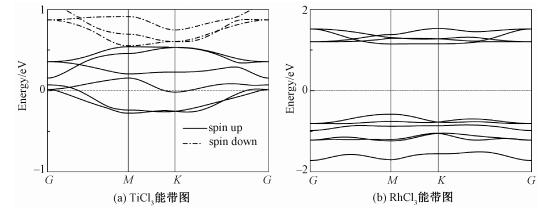
首先,二维材料TiCl3和RhCl3能带图(图 2)的计算表明,在费米面附近,TiCl3只存在自旋向上电子态,呈半金属性,自旋带隙约为0.6 eV。同时RhCl3呈半导体性,带隙约为1.62 eV。
|
Download:
|
| 图 2 TiCl3与RhCl3的能带图 Fig. 2 Band structures of TiCl3 and RhCl3 | |
之后,在电极磁化方向PC和APC情况下,分别计算小偏压范围(0~20 mV)和大偏压范围(0~0.6 V)内的自旋极化电流(I-V)曲线。其中小偏压范围内的极化电流如图 3(a)、3(b)所示。在PC构型下,自旋向上电子的电流随着偏压的增大而逐渐增大,而自旋向下电子态的电流基本保持不变,并且远远小于自旋向上电子的电流,使得在PC构型下的SIE高达100%且保持稳定。在APC构型下,自旋向上和自旋向下的电流值都随着电极两端所加偏压的增大而增大,但是数值都非常小,远小于PC情况下的电流值。由于在PC和APC两种情况下,电流值差异明显,使得体系的TMR值可以稳定保持在100%,并不随着电极两端所加偏压的改变而改变。稳定的TMR和SIE这些性质都说明该TiCl3/RhCl3/TiCl3自旋电子器件是很好的磁存储候选材料。

|
Download:
|
| 图 3 小偏压范围(0~20 mV)内不同磁构型下的自旋极化电流曲线和自旋注入效率及对应偏压下的TMR值 Fig. 3 The spin-polarized current-voltage (I-V) and SIE curves under PC and APC in the range of small bias (0-20 mV), and the TMR as a function of bias | |
当器件所加的偏压范围增加到0~0.6 V后,其自旋极化电流曲线如图 4所示,不同于小偏压范围下的电流趋势,在PC和APC两种电极磁化构型下,均存在一个阈值电压。在PC构型下,阈值电压为0.35 V,当所加偏压小于0.35 V时,自旋向上和向下的电流均很小,偏压大于0.35 V后,自旋向上的电流值迅速上升,远远超过自旋向下的电流值。在APC情况下,阈值电压变为0.4 V,与PC构型下的电流具有相同的变化趋势。通过计算两种不同磁化构型下的SIE发现,PC构型下的SIE仍保持100%不变,但是整个体系的TMR值会随着偏压的增大而逐渐减小。

|
Download:
|
| 图 4 大偏压范围(0~0.6 V)内不同磁构型下的自旋极化电流曲线和自旋注入效率及对应偏压下的TMR值 Fig. 4 The spin-polarized current-voltage (I-V) and SIE curves under PC and APC in the range of large bias (0-0.6 V), and the TMR as a function of bias | |
为了研究门电压对器件输运性质的影响,文中计算了PC构型下不同门电压下的电导值(如图 5(c)所示)。结果表明,随着门电压的逐渐增大,在自旋向上的电导值逐渐增大的同时,自旋向下的电导值逐渐减小,使得不同自旋的电流分离得更加彻底。为了更好地解释这一现象,文中还计算了不同门电压下体系的投影态密度(PDOS)图像(如图 5(a)、5(b)所示)。由计算结果可以看出:半金属电极TiCl3自旋向上的态主要分布在-0.3~0.6 eV的能量范围内,自旋向下的态主要分布在0.4~1.3 eV的能量范围内;而随着门电压的增大,中心区RhCl3的导带和价带逐渐向下移动,使得RhCl3的导带逐渐靠近费米能,与电极自旋向上的态有越来越多的重合部分,同时与自旋向下的态错开,从而在增加自旋向上态电导的同时减小了自旋向下态的电导。

|
Download:
|
| 图 5 不同门电压下的自旋向上和自旋向下的PDOS图像,电导和门电压为2 V时体系的透射谱以及偏压为0.35 V时的自旋向上态的散射态 Fig. 5 PDOS and conductance at different gate voltages for spin up states and spin down states, transmission at Vg=2 V, and the scattering state at 0.35 eV | |
为了详细研究这一现象,文中特别计算了门电压Vg=2 V时体系的透射谱(如图 5(d)所示)。从透射谱图像分析可知,在费米能附近,自旋向上态的透射谱值远远大于自旋向下透射谱值。并且当电极两端所加偏压为0.35 V时,自旋向上态有一个明显的峰值,而此时自旋向下态的透射系数为0。文中还计算了当前偏压下的散射态。散射态计算表明,此时自旋向上态的电子从左电极出发通过中心区到达右电极,但是不存在自旋向下的态。
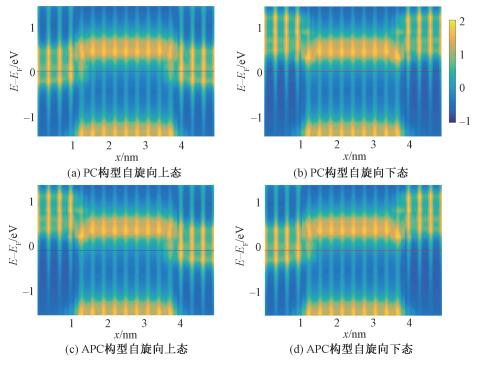
最后从PDOS图像出发解释上述结果。如图 6所示为零偏压下体系的PDOS图像,由图像分析发现费米能级位于RhCl3的带隙中,距导带底大约0.3 eV。所以当体系处在小偏压范围内计算其I-V曲线及其他物理性质时,此时的电子从左电极出发到达右电极时,需要隧穿通过中心区的势垒。而当所加偏压大于0.3 V时,左电极的电子可以通过中心区的导带,从而到达右电极。由于两种情况下的输运机制不同,导致在偏压大于0.3 V时,器件的电流值会远大于小偏压范围内的电流值。如图 6所示,在小偏压范围(0~20 mV)内计算I-V曲线时,在PC构型下,左右电极在费米能附近只存在自旋向上态,所以此时只有自旋向上的电子通过隧穿到达右电极,即自旋向上的电流远大于自旋向下的电流。在APC构型下,费米能附近,只有右(左)电极存在自旋向上(下)的态,左(右)电极自旋向上(下)的态基本为0,所以由于只有其中一个电极存在自旋向上(下)的态,这就限制了自旋极化电流的通过,使得其量级非常小;而当所加偏压大于0.35 V时,在PC构型下,此时自旋向上的态可以通过中心区RhCl3的导带到达右电极,由于输运机制的改变,此时的电流值迅速上升。同样,在APC构型下,当电压达到0.4 V时,电流值迅速上升。
|
Download:
|
| 图 6 PC和APC构型下自旋向上和自旋向下态的PDOS图像 Fig. 6 PDOS for spin up and spin down states under PC and APC | |
搭建二维自旋电子器件TiCl3/RhCl3/TiCl3,即半金属TiCl3做电极、半导体RhCl3做中心区,并计算其不同偏压范围下的极化电流曲线。通过计算发现在小偏压范围(0~20 mV)内,体系的隧穿磁电阻即TMR值会保持在100%稳定不变,并且在左右电极磁化方向平行的情况下,体系的自旋注入效率SIE也保持在100%;在大偏压范围(0~0.6 V)内,PC和APC两种构型的阈值电压分别是0.35和0.4 V,超过阈值电压后,体系的电流值迅速上升。最后通过计算体系的PDOS图像,对上述物理现象做出解释。另外,不同门电压下体系的PDOS图像和电导值的计算说明,随着门电压的增大,不同自旋的电流会被更好地分离。
感谢苏刚、王正川、朱振刚、闫清波教授在研究过程中给与的指导和建议。感谢鸿之微科技(上海)股份有限公司在软件应用上给与的帮助。| [1] |
Baibich M N, Broto J M, Fert A, et al. Giant magnetoresistance of (001)Fel(001) Cr magnetic snperlattices[J]. Physical Review Letters, 1988, 61: 2472-2475. Doi:10.1103/PhysRevLett.61.2472 |
| [2] |
Binasch G, Griinberg P, Saurenbach F, et al. Enhanced magnetoresistance in layered magnetic structures with antiferromagnetic interlayer exchange[J]. Physical Review B, 1989, 39: 4828-4830. |
| [3] |
Ikeda S, Hayakawa J, Ashizawa Y, et al. Tunnel magnetoresistance of 604% at 300 K by suppression of Ta diffusion in CoFeB-MgO-CoFeB pseudo-spin-valves annealed at high temperature[J]. Applied Physics Letters, 2008, 93: 082508. Doi:10.1063/1.2976435 |
| [4] |
Miyazaki T, Tezuka N. Giant magnetic tunneling effect in Fe/Al2O3/Fe junction[J]. Journal of Magnetism and Magnetic Materials, 1995, 139: L231-L234. Doi:10.1016/0304-8853(95)90001-2 |
| [5] |
Wen Z C, Sukegawa H, Mitnai S, et al. Tunnel magnetoresistance in textured Co2FeAl/MgO/CoFe magnetic tunnel junctions on a Si/SiO2 amorphous substrate[J]. Applized Physics Letters, 2011, 98: 192505. Doi:10.1063/1.3587640 |
| [6] |
Wulfhekel W, Klaua M, Ullmann D, et al. Single-crystal magneto tunnel junctions[J]. Applized Physics Letters, 2001, 78: 509-511. Doi:10.1063/1.1342778 |
| [7] |
Moodera J S, Kinder L R, Wong T M, et al. Large magnetoresistance at room temperature in ferromagnetic thin film tunnel junctions[J]. Physical Review Letters, 1995, 74: 3273-3276. Doi:10.1103/PhysRevLett.74.3273 |
| [8] |
Currivan-Incorvia J A, Siddiqui S, Dutta S, et al. Logic circuit prototypes for three-terminal magnetictunnel junctions with mobile domain walls[J]. Nature Communications, 2016, 7: 10275. Doi:10.1038/ncomms10275 |
| [9] |
Wolf S A, Awschalom D D, Buhrman R A, et al. Spintronics:a spin-based electronics vision for the future[J]. Science, 2001, 294: 1488-1495. Doi:10.1126/science.1065389 |
| [10] |
Novoselov J S, Geim A K, Morozov S V, et al. Electric field effect in atomically thin carbon films[J]. Science, 2004, 306: 666-669. Doi:10.1126/science.1102896 |
| [11] |
Li L K, Yu Y J, Ye G J, et al. Black phosphorus field-effect transistors[J]. Nature Nanotechnology, 2014, 9: 372-377. Doi:10.1038/nnano.2014.35 |
| [12] |
Hong T, Chamlagain B, Lin W, et al. Polarized photocurrent response in black phosphorus field-effect transistors[J]. Nanoscale, 2014, 6: 8978-8983. Doi:10.1039/C4NR02164A |
| [13] |
Mak K F, Lee C G, Home J, et al. Atomically thin MoS2:a new direct-gap semiconductor[J]. Physical Review Letters, 2010, 105: 136805. Doi:10.1103/PhysRevLett.105.136805 |
| [14] |
Wang Q H, Kalantar-Zadeh K, Kis A, et al. Electronics and optoelectronics of two-dimensional transition metal diachalcogenides[J]. Nature Nanotechnology, 2012, 7: 699-712. Doi:10.1038/nnano.2012.193 |
| [15] |
Leong W S, Li Y, Luo C, et al. Tuning the threshold voltage of MoS2 field-effect transistors via surface treatment[J]. Nanoscale, 2015, 7: 10823-10831. Doi:10.1039/C5NR00253B |
| [16] |
Jiang L F, Zeng H B. Comment on "Strongly luminescent monolayered MoS2 prepared by effective ultrasound exfoliation"[J]. Nanoscale, 2015, 7: 4580-4583. Doi:10.1039/C3NR06641J |
| [17] |
Sheng X L, K.Nikolic' B. Monolayer of the 5d transition metal trichloride OsCl3:a playground for two-dimensional magnetism, room-temperature quantum anomalous Hall effect, and topological phase transitions[J]. Physical Review B, 2017, 95: 201402. Doi:10.1103/PhysRevB.95.201402 |
| [18] |
Weber D, Schoop L M, Duppel V, et al. Magnetic properties of restacked 2D spin 1/2 honeycomb RuCl3 Nanosheets[J]. Nano Letters, 2016, 16: 3578-3584. Doi:10.1021/acs.nanolett.6b00701 |
| [19] |
McGuire M A, Dixit H, Cooper V R, et al. Coupling of crystal structure and magnetism in the layered, ferromagnetic insulator CrI3[J]. Chemistry of Materials, 2015, 27: 612-620. Doi:10.1021/cm504242t |
| [20] |
Huang B, Clark G, Navarro-Moratalla E, et al. Layer-dependent ferromagnetism in a van der Waals crystal down to the monolayer limit[J]. Nature, 2017, 546: 270-273. Doi:10.1038/nature22391 |
| [21] |
Zhou Y G, Lu H F, Zu X T, et al. Evidencing the existence of exciting half-metallicity in two-dimensional TiCl3 and VCl3 sheets[J]. Scientific Reports, 2015, 6: 19407. |
| [22] |
Zacharia R, Ulbricht H, Tobias H. Interlayer cohesive energy of graphite from thermal desorption of polyaromatic hydrocarbons[J]. Physical Review B, 2004, 69: 155406. Doi:10.1103/PhysRevB.69.155406 |
| [23] |
Kresse G, Furthmuller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set[J]. Physical Review B, 1996, 54: 11169-11186. Doi:10.1103/PhysRevB.54.11169 |
| [24] |
Perdew J P, Burke K, Ernzerhof M. Generalized gradient approximation made simple[J]. Physical Review Letters, 1996, 77(18): 3865-3868. Doi:10.1103/PhysRevLett.77.3865 |
| [25] |
Taylor J, Guo H, Wang J. Ab initio modeling of quantum transport properties of molecular electronic devices[J]. Physical Review B, 2001, 63: 245407. Doi:10.1103/PhysRevB.63.245407 |
 2020, Vol. 37
2020, Vol. 37 


