Point matching plays a central role on computer vision such as action recognition[1], multi-target tracking[2], image retrieval[3], etc. The purpose of point matching is to determine correspondence between two point sets. There are some traditional algorithms to handle it, such as random sample and consensus (RANSAC)[4], graph-based point pattern matching[5], etc. Most of the traditional algorithms are alternated between calculating parameters of transformation and getting correspondence to obtain the optimal solution. This means that different models need to learn different transformation parameters. Meanwhile, as the number of points increases, execution time of system increases notably. If we can directly get accurate correspondence, we will be able to enhance the efficiency of matching problem. Actually, the point set is a sequence of feature vectors and the correspondence can be seen as a special form of permutation. Inspired by these facts, we propose a genetic model based on recurrent neural network (RNN)[6] to solve the problem.
RNN has become a popular choice for modeling variable-length sequences for more than three decades. Long short-term memory (LSTM)[7] with the ability of analyzing data with long range temporal dependencies makes it possible to handle long sentences using RNN. RNN recently showed impressive performance on several sequence prediction problems including machine translation[8], contextual parsing[9], image captioning[10], and even video description[11]. In particular, Vinyals et al.[12], Milan et al.[13], and Bello et al.[14] used RNN to tackle combinatorial optimation problem.
Most of models to approach sequential problem belong to a family of encoder-decoder[8, 15] that consists of two RNNs. One RNN encodes the source sentence into a fix-length vector, and the other decodes target sequences from the vector. The whole encoder-decoder system jointly maximizes the conditional probability of target sequence based on source sequence. However, compressing all necessary information of input sequence into a fixed-length vector is a bottleneck problem that limits the performance of encoder-decoder architecture. In order to address this issue, Bahdanau et al.[16] proposed a content-based attentional mechanism which encodes input sentence into a sequence of vectors and chooses a subset of these vectors adaptively while decoding the translation. Nonetheless, the size of output dictionary needs to be fixed before designing model. So we can not directly apply this to combinatorial problem where the size of output dictionary depends on the length of input sequence. Pointer network (Ptr-Net)[12] provides a new architecture which addresses this limitation by repurposing the attention mechanism to create pointer to input elements.
Point matching is also a special kind of combinatorial optimization problem that is to obtain the optimal corresponding references, which can be modeled by Ptr-Net. However, Ptr-Net does not take full advantage of the correspondences between two point sets owing to the fact that output is a member of input elements at each time series. We propose multi-pointer network (MPN), which draws idea from multi-label classification[17-18], to address this limitation by pointing out a set of input elements.
To our knowledge, the present study is the first study to empirically evaluate the ability of RNN to output correspondences of two sets in a purely data driven fashion (i.e., when we only have examples of inputs and desired outputs). Experiments show that MPN can address matching problem with large-scale transformation efficiently and simply. On the other hand, MPN can also be extended to other combinatorial optimization problem.
This paper is organized as follows. In section 2, we briefly introduce the encoder-decoder framework, Ptr-Net, and multi-label classification. Our model based on the combination of multi-label classification and Ptr-Net is described in details in section 3. To test the effectiveness of our model, we run and analyze experiment results, including extensive comparisons with multiple rigid transformation and computing Delaunay Triangulation in section 4. Finally, we summarize the main contribution of our work and discuss the future direction.
1 BackgroundRNN is a class of artificial neural network which uses the internal memory to process input sequence with arbitrary length. Given a set of N pairs (Xi, Yi)i=1N, where (Xi, Yi) is the ith pair of input and its corresponding target. The goal of the model is to estimate the conditional probability P(Yi|Xi), where Xi={x1i, x2i, …, xiTx} and Yi={y1i, y2i, …, yiTy}. It is noteworthy that the length of the input sequence Tx may differ from its corresponding output sequence Ty. The parameters θ of RNN can be estimated by maximizing the cost function
| $ J(\theta ) = \frac{1}{N}\sum\limits_{n = 1}^N {{\rm{log}}} P({Y^n}|{X^n};\theta ). $ | (1) |
In this case, it is reasonable to model each example using the chain rule to decompose it as follows (for the sake of brevity, we omit the index i):
| $ P(Y|X;\theta ) = \prod\limits_{t = 1}^{{T_y}} P ({y_t}|{y_1}, {y_2}, \cdots , {y_{t - 1}}, X;\theta ). $ | (2) |
The strategy of the encoder-decoder model is to map input sequence to a fixed-length vector c with one RNN, and then to map the vector to target sequence with another RNN. We call the former RNN the encoder and the latter the decoder. The most common encoder approach is to use one RNN such that
| $ {e_t} = {f_1}({x_t}, {e_{t - 1}}), $ | (3) |
where f1 is the activation function of encoder RNN, et-1and et are the states of encoder at time t-1 and t, respectively. Generally, we choose LSTM architecture as activation function f1 which is suitable for long range temporal dependencies. Then we get the vector
| $ \mathit{\boldsymbol{c}} = q({e_1}, {e_2}, \cdots {e_{{T_x}}}), $ | (4) |
where q is another nonlinear function. In Ref.[8], the fixed-dimensional representation c is the last hidden state of LSTM. Then we use another standard LSTM formulation f2 whose initial hidden state is c, to obtain hidden state of the decoder dt at time t,
| $ {d_t} = {f_2}({d_{t - 1}}, {y_{t - 1}}, \mathit{\boldsymbol{c}}). $ | (5) |
The conditional distribution of the next symbol is
| $ P({y_t}|\mathit{\boldsymbol{c}}, {y_1}, \cdots {y_{t - 1}};\theta ) = g({d_t}, {y_{t - 1}}, \mathit{\boldsymbol{c}}), $ | (6) |
where g is an activation function. Generally, the function is represented with a softmax over all words in the dictionary. Thus, we need to train different models which correspond to different sizes of dictionary. So we can not straightforwardly extend this model to problem for which the size of output dictionary depends on the length of input sequence.
1.2 Pointer networkPointer network (Ptr-Net) is an effective model repurposing a recently proposed mechanism of neural attention[16] to solve combinatorial optimization problem where output dictionary size is equal to the length of input sequence. It differs from previous attention attempt in using attention as a pointer to select a member of source sequence as target, instead of using attention to compute the weighted sum of these encoder hidden units at each decoder step.
The encoder-decoder model normally uses a softmax distribution over a fixed-length output dictionary to compute P(yt|c, y1, …yt-1; θ). This prevents us from learning solutions to problem where output dictionary size depends on the number of elements in the input sequence. To overcome these, Ptr-Net does not use attention mechanism to blend hidden units of an encoder ej to context vector, but instead uses uji as pointer to select input elements at each decoder step. The modified attention mechanism is shown as follows:
| $ u_j^i = {\mathit{\boldsymbol{v}}^{\rm{T}}}{\rm{tan}}{\kern 1pt} {\kern 1pt} h({W_1}{e_j} + {W_2}{d_i}), j \in (1, 2, \cdots , {T_x}), $ | (7) |
| $ P({y_t}|{y_1}, {y_2}, \cdots , {y_{t - 1}}, X;\theta ) = {\rm{soft}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{max}}({\mathit{\boldsymbol{u}}^i}), $ | (8) |
where softmax normalizes the vector ui (of length Tx) to be an output distribution over the dictionary of inputs, and v, W1, and W2 are learnable parameters of the output model.
In Ref.[12], authors trained Ptr-Net to output satisfactory solutions to three challenging geometric problems, computing planar convex hulls, Delaunay Triangulation, and symmetric planar travelling salesman problem (TSP). Ptr-Net is a new architecture to provide novel methods for complex combinatorial optimization where the output sequence corresponds to positions in an input sequence. For the point matching problem that requires to assign labels to elements of the input, it is necessary to simultaneously output corresponding points at decoding time.
1.3 Multi-label classificationMulti-label classification is the supervised learning problem where each object is represented by a single instance while associated with a set of labels instead of a single label. The task is to predict the label sets of unseen instances through analyzing training instances with known label sets. It helps to address the problem which has a certain degree of correlation between labels. This characteristic provides us an important theoreticed gist which can preferably improve Ptr-Net to solve point matching. At the present, researches that apply LSTMs to multi-label classification tasks are quite limited. Liu and Ramakrishnan[19]formulated music composition as a multi-label classification task, using sigmoidal output units. Yeung et al.[20] used LSTM network with multi-label method to recognize actions in videos. Recently, Lipton et al.[21] recognized patterns in multivariate time series of clinical measurements using replicated targets at each sequence step in the medical domain. However, we could not locate any reported works using LSTMs with multi-label classification on combinatorial optimization domain, especially the point matching problem.
2 The proposed modelMatching problem is to determine correspondence between the reference set A:{pi=(xi, yi):i=1, 2, …, m} and the sensed set B:{qi=(xi, yi):i=1, 2, …, n}. We can simply add a special end-of-set symbol ⇒ at the end of reference set, which connects two sets as a sequence. An ordered set of vertices replace the related correspondences between point sets. In this way, we can make use of the encoder-decoder framework to solve point matching problem. Figure 1 shows a simple example that how we turn the matching problem to sequential problem. Set A={p1, p2, p3} and set B={q1, q2, q3} is shown in the left of Fig. 1. Let the correspondence of two sets is (p1, q2), (p2, q3), (p3, q1). In the right part, we show the target vector of each time series. The dotted circle of each vector represents the end of set A.

|
Download:
|
|
Fig. 1 The schematic diagram showing how to turn the matching problem into the sequential problem |
|
In this paper, we propose a novel model named as multi-pointer network. The model can generate a set of elements simultaneously at each series time by introducing multi-label classification idea into the Ptr-Net. Figure 2 is a schematic of the multi-pointer Network. We use the symbol ⇒ to represent the end of set A, symbol ⇔ to represent the end of encoder and symbol 〈ɡ〉 to represent input of the first decoder step. In the following article of this section, we will describe the model in detail.
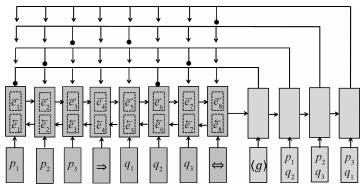
|
Download:
|
|
Fig. 2 A depiction of the multi-pointer network |
|
The regular RNN reads the sequence in left-to-right order. However, future input information coming up later is also important for prediction. To overcome the limitation, we use the bidirectional recurrent neural network (Bi-RNN)[22] that can be trained using all available input information in the past and future of a specific time frame.
A Bi-RNN consists of two parts, one part for positive time direction (forward states) and the other part for negative time direction (backward states). Firstly, positive RNN
| $ {e_i} = \left[ {\begin{array}{*{20}{c}} {\overrightarrow {{e_i}} }\\ {\overleftarrow {{e_i}} } \end{array}} \right]. $ | (9) |
Note that there are no interactions between the two types of state neurons.
With both time directions taken care of in the same network, input sequence can directly include future information without the need for delays. So we can summarize not only the preceding point, but also the following point to adapt point matching problem. In experiments, we use LSTM as the activation function of the positive and negative RNN. In Fig. 2, the two dashed rectangle boxes in the bigger boxes represents the process of the bidirectional RNN.
2.2 Decoder-multi-pointer networkFor point matching, we define matching point-pair as the target output of each time series in training process. After sorting the points of two sets, we construct a series of objective vectors that elements of each one are zero besides the position of the matching point-pair (see Fig. 1). Hence, we need to output a set of the input sequences simultaneously at the decoder part. Drawing the idea on multi-label classification, we present a simple modification of the Ptr-Net. Now let us go through the details of the new model.
Firstly, we still use equation (7) to calculate the vector ui to be “attention” mask over the inputs. Then a different approach is adapted to obtain the conditional distribution at each time step.
| $ P({y_t}|{y_1}, {y_2}, \cdots , {y_{t - 1}}, X;\theta ) = {\rm{sigmoid}} ({\mathit{\boldsymbol{u}}^i}). $ | (10) |
What makes our model different from Ptr-Net is that we use sigmoid function instead of softmax function to fit the multi-label classification loss function. This allows us to maintain that the output of every time series is the matching point-pair or points of other geometry structure.
We generate outputs in chronological order at each sequence step. Then we adapt cross entropy method to calculate the loss function,
| $ {\rm{loss}} (Y, \hat Y) = \frac{1}{N}\sum\limits_{n = 1}^N { {\rm{loss}} } ({Y^n}, {\hat Y^n}), $ | (11) |
| $ {\rm{loss}} ({Y^n}, {\hat Y^n}) = \frac{1}{T}\sum\limits_{t = 1}^T - ((y_t^n \cdot {\rm{log}}\hat y_t^n) + z_t^n \cdot {\rm{log}}\hat z_t^n), $ | (12) |
where znt=1-ynt,
Our model is specifically aiming at problems whose outputs of every time series are high correlation. Ptr-Net tends to solve problems where outputs are discrete and dependent on its location in the input sequences. Our model mines the underlying information between two point sets. In this manner, information can be spread throughout two point sets which greatly improves the accuracy of matching problems. Besides, the multi-pointer network can also be applied to the problem of combined structural optimization, like Delaunay triangulation.
3 ExperimentsIn this section, we take a brief introduction of experimental details and analyze the results. Firstly, contrast experiment is done to test the impact of using Bi-RNN. Then, in order to verify whether our model could handle point matching and be more efficient than the Ptr-Net, we run the following experiments on artificial data for tasks. Finally, to confirm the model’s generalization, we compare our model with the typical Ptr-Net on Delaunay Triangulation.
3.1 Experimental detailsAcross all experiments, we use mini-batches of 128 point set sequences and embed the two coordinates of each point in a 256-dimensional space. At encoder step, the Bi-RNN we used consists of the forward and the backward LSTM cells with 128 hidden units. At decoder step, we utilize LSTM cells with 256 hidden units and one attention glimpse[23] to aggregate the contributions of different parts of the input sequence. According to the experimental results of Ref.[14], we also adopt only one glimpse to reach the trade-off between performance and cost latency in our experiments. We initialize all of the LSTM’s parameters with the uniform distribution between -0.08 and 0.08. And we clip the L2 norm of our gradients to 2.0 to avoid exploding gradient problem. We train our model with the Adam optimizer and decay every 5 000 steps by a factor of 0.96 with an initial learning rate of 10-3. The layer of the encoder and the decoder LSTM is one. Even though there are likely higher accuracy to be obtained by tuning the model, we consider that using the same model hyperparameters on all rigid transformations makes the paper stronger. Our model is trained in Tensorflow framework[24].
3.2 Data descriptionTo fully exploit the performance of multi-pointer network, we set up different types of rigid transformation and different sizes of point sets for comparative experiment. First, a random point set A samples from a uniform distribution in [1,2]×[1,2]. Then, another point set B is generated from rigid transformation on A. To avoid the vertex coordinates of point is less than zero, some correction is made on set B. The impact of network on point matching problem is discussed at different sizes and different kinds of transformation in more detail below.
3.2.1 DatabaseWe set two different fixed-size of sets 6-to-6 (the point number of set A is 6, and the point number of set B is 6), 10-to-10 and one random number size of sets 5-10-to-5-10 (the number of set A is a random number of 5-10, and the number of set B is a random number of 5-10,
We adapt a different translation approach from a traditional enterprise deployment. First, we sample from uniform distribution [0, 1] to generate dx and dy respectively. Then, we apply a linear function to ensure the length of translation vector equal to 1 and leave the orientation of vector unchanged. In this way, the translation is no longer the pixel level which has a more extensive adaptability.
3.2.3 RotationThree different dynamic intervals, [0, 45°], [0, 90°], [0, 135°] are built to evaluate the intervals on the rotation performance of the new model in this paper. We also verify the fact that the number of sets has great impact on experiment results.
3.2.4 ScalingTo verify the similarity transformation, the scaling parameters we adopted is from 50% to 150%.
3.3 Results and analysesTo measure the accuracy we use average correct point pair ratio (ACPPR). The correct point pair ratio is defined as follows:
| $ {\rm{ACPPR }} = {\rm{ }}\frac{{{\rm{correct}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{matching}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{pair}}{{\rm{s}}^{\rm{'}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{number}}}}{{{\rm{all}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{the}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{correct}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{matching}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{pair}}{{\rm{s}}^{\rm{'}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{number}}}}. $ | (13) |
In this paper, all ACPPR values are calculated from at least 500 experiments. This section is mainly divided into two parts. The first part we verify the effectiveness of the bidirectional-LSTM. The second part is an analytical and comparative study of different version of transformations.
3.3.1 Bidirectional RNNWe test the impact of using bidirectional RNN (Bi-RNN) on transformation and rotation. The database we adopted is the set with random number size 5-10-to-5-10 and the interval of rotation angles is [0°, 45°]. Figure 3 shows the importance of Bi-RNN in the process of training. Through observation we find that using Bi-RNN has faster convergence ability and smaller loss than the model without it.

|
Download:
|
|
Fig. 3 Comparison of the experimental results in translation and rotation with and without Bi-RNN |
|
The results of experiments verify that our new method can effectively solve matching problem with various transformations and different sizes of data set. Firstly, we verify the effect on various rotation angle interval. The results are presented in Table 1. Then, comparison between Ptr-Net (P) with our multi-pointer network (M) is carried out. Table 2 shows the comparing experimental results on different transformation with the fixed angle θ=30°. By leveraging the constraint of the multi-label classification, the network can be better to reinforce the connection between two sets, thus the accuracy rate is improved significantly.
|
|
Table 1 Matching results with various rotation angles θ |
|
|
Table 2 Comparison between Ptr-Net (P) with our MPN (M) of different transformations |
In this section, we consider the Delaunay triangulation, which is another intensively studied problem in computer science and mathematics. Given a set P with points in a plane, Delaunay triangulation is a triangulation such that there is no point from the set P in its interior. During the training phase, the labels of the output Sp={S1, S2, …, Sm(P)} is the corresponding sequences representing the triangulation of point set. Each Si represents the vertices of the i triangle, the integers of triple which is from 1 to n corresponding to the position of set P.
In experiments, we sample from a uniform distribution in [0, 1]×[0, 1] to create the training data. Ref.[23] shows the order of the sequence to impact the experiment performance. Therefore, we order the triangulations by their incenter coordinats in experiments. Compared to the Ptr-Net, we do not have to consider the problem as a consequence, any permutation of its elements will represent the same triangulation. Our experiment is about 5 points of the set to achieves in average 0.45% improvement.
4 ConclusionIn this paper we present empirical study using RNN to solve point matching problem. By analyzing the matching problem using mathematical method, we transform it into sequential manner. We propose a new end-to-end network, which is based on multi-label classification, to improve the Ptr-Net. Experimental results show that the proposed method effectively solves translation and other rigid transformation with large-scale. In this way, we can rapidly gain the corresponding relations of point sets in the inference. Moreover, our method can be extend to solve other problems of combined structural optimization.
In future, we will try to design a more effective model to raise accuracy. Through the trained model we can obtain correspondences directly. On this foundation, we can calculate parameters of transformation much more quickly based on the traditional method like RANSAC. In the meantime, the network model proposed in this paper can be generalized to the problem of multi-dimension point sets matching. We are also excited about the possibility of using this method to other combinatorial optimization problem which requires to assign labels to elements of the input.
| [1] |
Brendel W, Todorovic S. Learning spatiotemporal graphs of human activities[C]//International Conference on Computer Vision. Barcelona: IEEE, 2011: 778-785.
|
| [2] |
Zheng D, Xiong H, Zheng Y F, et al. A structured learning-based graph matching for dynamic multiple object tracking[C]//International Conference on Image Processing. Brussels: IEEE, 2011: 2333-2336.
|
| [3] |
Chu L, Jiang S, Wang S, et al. Robust spatial consistency graph model for partial duplicate image retrieval[J]. IEEE Transactions on Multimedia, 2013, 15(8): 1982-1996. DOI:10.1109/TMM.2013.2270455 |
| [4] |
Fischler M A, Bolles R C. Random sample consensus:a paradigm for model fitting with applications to image analysis and automated cartography[J]. Communications of the ACM, 1981, 24(6): 381-395. DOI:10.1145/358669.358692 |
| [5] |
Bolles R C. Robust feature matching through maximal cliques[J]. Proceedings of SPIE-The International Society for Optical Engineering, 1979, 182: 140-149. |
| [6] |
Rumelhart D E, Hinton G E, Williams R J, et al. Learning representations by back-propagating errors[J]. Nature, 1988, 323(6088): 696-699. |
| [7] |
Hochreiter S, Schmidhuber J. Long short-term memory[J]. Neural Computation, 1997, 9(8): 1735-1780. DOI:10.1162/neco.1997.9.8.1735 |
| [8] |
Sutskever I, Vinyals O, Le Q V, et al. Sequence to sequence learning with neural networks[C]//Neural Information Processing Systems. Montreal: 2014: 3104-3112.
|
| [9] |
Vinyals O, Kaiser L, Koo T, et al. Grammar as a foreign language[C]//Neural Information Processing Systems. Montreal: 2015: 2773-2781.
|
| [10] |
Vinyals O, Toshev A, Bengio S, et al. Show and tell: a neural image caption generator[C]//Computer Vision and Pattern Recognition. Boston: IEEE, 2015: 3156-3164.
|
| [11] |
Donahue J, Hendricks L A, Guadarrama S, et al. Long-term recurrent convolutional networks for visual recognition and description[C]//Computer Vision and Pattern Recognition. Boston: IEEE, 2015: 2625-2634.
|
| [12] |
Vinyals O, Fortunato M, Jaitly N, et al. Pointer networks[C]//Neural Information Processing Systems. Montreal: 2015: 2692-2700.
|
| [13] |
Milan A, Rezatofighi S H, Garg R, et al. Data-driven approximations to NP-hard problems[C]//Proceedings of the Thirty-First AAAI Conference on Artificial Intelligence. San Francisco: AAAI Press, 2017: 1453-1459.
|
| [14] |
Bello I, Pham H, Le Q V, et al. Neural combinatorial optimization with reinforcement learning[J]. arXiv preprint arXiv:1611.09940, 2016. |
| [15] |
Cho K, Van Merrienboer B, Gulcehre C, et al. Learning phrase representations using RNN encoder-decoder for statistical machine translation[C]//Empirical Methods in Natural Language Processing. Doha: Association for Computational Linguistics, 2014: 1724-1734.
|
| [16] |
Bahdanau D, Cho K, Bengio Y. Neural machine translation by jointly learning to align and translate[J]. arXiv preprint arXiv:1409.0473, 2014. |
| [17] |
Zhang M, Zhou Z. A review on multi-label learning algorithms[J]. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(8): 1819-1837. DOI:10.1109/TKDE.2013.39 |
| [18] |
Tsoumakas G, Katakis I. Multi-label classification:an overview[J]. International Journal of Data Warehousing and Mining, 2007, 3(3): 1-13. |
| [19] |
Liu I, Ramakrishnan B. Bach in 2014:music composition with recurrent neural network[J]. arXiv preprint arXiv:1412.3191, 2014. |
| [20] |
Yeung S, Russakovsky O, Jin N, et al. Every moment counts:dense detailed labeling of actions in complex videos[J]. International Journal of Computer Vision, 2018, 126(2-4): 375-389. DOI:10.1007/s11263-017-1013-y |
| [21] |
Lipton Z C, Kale D C, Elkan C, et al. Learning to diagnose with LSTM recurrent neural networks[J]. arXiv preprint arXiv:1511.03677, 2015. |
| [22] |
Schuster M, Paliwal K K. Bidirectional recurrent neural networks[J]. IEEE Transactions on Signal Processing, 1997, 45(11): 2673-2681. DOI:10.1109/78.650093 |
| [23] |
Vinyals O, Bengio S, Kudlur M. Order matters:sequence to sequence for sets[J]. arXiv preprint arXiv:1511.06391, 2015. |
| [24] |
Abadi M, Barham P, Chen J, et al. Tensorflow: a system for large-scale machine learning[C]//Operating Systems Design and Implementation. Savannah: USENIX, 2016, 16: 265-283.
|
 2020, Vol. 37
2020, Vol. 37 


