合肥市位于华东地区，是国家重要的教育科研基地，作为安徽省的省会城市，在经济发展中占据重要地位，其房地产市场也受到各方面的关注。住宅建设关乎社会稳定、经济发展，是城市产业经济发展的重要研究课题。随着城市的快速发展，城市的空间格局也发生改变，房地产市场发展进入新的阶段。近年来住宅价格上升过快，2016年的合肥楼市涨幅全国第一，高房价对于普通百姓家庭而言负担较重。而影响房价的因素很多，在此背景下，研究影响房价波动的因素十分重要，可以为相关部门规范当前过热的房地产市场提供依据。

从现有的研究成果看，Cliff和Ord^[1]在普通线性回归模型中加入空间效应，提出空间自回归模型，并对模型进行参数估计和检验。Anselin^[2-3]在空间自回归模型的基础上，提出广义空间自回归模型，Pace等^[4]指出可以在模型中加入空间权重来分析房地产。Rey和Dev^[5]运用空间自相关模型，从空间计量的角度出发，对美国各个地区经济做实证实验，分析其收敛性，并得出结论认为美国的经济增长呈现收敛的趋势。Ismail^[6]探讨住宅市场特征建模背景下的空间自相关问题，在HPM模型的基础上，讨论引入空间自相关的原因、检测方法以及模型的设定方法。Bitter等^[7]将空间自相关引入特征价格模型以及空间误差模型，分析房地产价格的空间交互作用，结果得出住房特征的边际价格与空间位置有显著关系。Holly等^[8]利用空间计量模型，探讨英国房地产价格的空间溢出效应，并得出结论认为纽约的房价对英国房价有一定的影响。Elod^[9]利用22个国家的房价数据研究得出人口老龄化对房地产价格变动有重要影响。

近年来很多国内学者运用空间计量方法进行研究。刘洪玉^[10]利用1995—2002年国内城市住宅价格指数以及宏观经济变量数据对房价的影响关系进行实证研究，结果表明，经济基本面对住宅价格存在显著影响。温海珍和贾生华^[11]利用空间计量模型方法对杭州市2008年住宅小区进行分析，结果表明，住宅价格的空间自相关呈显著正相关，空间自相关模型的估计结果优于传统模型。王鹤^[12]运用全局自相关和局部自相关检验国内房价的空间自相关性，结果显示房价呈正相关关系，利用空间面板模型对全国范围及东部、中部、西部地区的住宅价格进行分析，结果表明东、中、西部区域房价的影响因素各不相同。姚丽等^[13]研究郑州市新建住宅房价的空间自相关性，发现郑州市住宅价格存在显著的空间正相关，利用空间计量模型，发现空间溢出效应和交通可达性对房价的影响也十分显著。

之前的研究成果没有考虑到变点对空间自相关的影响，本文在网络自回归模型的基础上，选取合肥市的住宅价格数据，考虑到房地产价格的剧烈变动对模型有一定的影响，拓展了Jin等^[14]的两阶段变点估计方法，找出房价的变点，分别对变点前后的时间段做空间自相关分析，再分别建立空间网络自回归模型，从而找出影响房价的因素。

1 模型介绍 1.1 全局空间自相关

空间权重矩阵是空间滞后变点模型的重要组成部分，对于模型求解有着不可忽视的作用。空间权重矩阵的构建直接影响空间计量模型的估计。本文采取0-1权重矩阵，根据两个小区之间的距离来确定空间权重，两个小区之间的距离在d以内表示为1，距离在d以外记为0。在使用空间权重矩阵之前，需要对空间权重矩阵进行标准化处理，使得每一行的元素之和为1。在设定空间网络自回归变点模型之前，首先要检验之间是否存在空间相关性，全局空间自相关描述了属性值在整个研究范围内的空间特征，有很多表示全局空间自相关的指标和方法，最常用的是Moran’s I指数。Moran’s I衡量空间要素的相互关系，与统计学中的相关系数类似，它的值在-1~1之间，如果大于零，则表示存在正相关, 小于零则表示存在负相关，等于零则表明不存在空间相关性，各要素之间差异较小，空间上均衡发展，其计算公式如下

$ I=\frac{\sum_{i}^{n} \sum_{j \neq i}^{n} W_{i j}\left(X_{i}-\bar{x}\right)\left(X_{j}-\bar{x}\right)}{\frac{1}{n} \sum_{i}^{n}\left(X_{i}-\bar{x}\right)^{2} \sum_{i}^{n} \sum_{j \neq i}^{n} W_{i j}}. $

(1)

式中：$\bar{X}=\frac{1}{n} \sum i=1^{n} X_{i}$, X_i是第i个地区的观测值，n为地区的总数；W_ij为空间权重矩阵的任一元素。

1.2 空间网络自回归变点模型

参考Zhu等^[15]的网络自回归模型，在网络自回归模型的基础上加入空间权重矩阵W，并且有s个变点在1 < a₁ < … < a_s < T的空间网络自回归变点模型如下：

$ \begin{array}{l} {\mathit{\boldsymbol{y}}_t} = \sum\limits_{l = 1}^s {\left( {\sum\limits_{j = 1}^q {{\mathit{\boldsymbol{x}}_{t, j}}} {\delta _{j, l}} + {\rho _l}W{\mathit{\boldsymbol{y}}_{t - 1}}} \right)} I\left( {{a_l} < t \le T} \right) + \sum\limits_{j = 1}^q {{X_{t, j}}} {\mathit{\boldsymbol{\beta }}_j} + \rho W{\mathit{\boldsymbol{y}}_{t - 1}} + {\mathit{\boldsymbol{\varepsilon }}_t}\\ = {\mathit{\boldsymbol{X}}_t}\left[ {\mathit{\boldsymbol{\beta }} + \sum\limits_{l = 1}^s {{\mathit{\boldsymbol{\delta }}_l}} I\left( {{a_l} < t \le T} \right)} \right] + \left[ {\rho + \sum\limits_{l = 1}^s {{\rho _l}} I\left( {{a_l} < t \le T} \right)} \right]W{\mathit{\boldsymbol{y}}_{t - 1}} + {\varepsilon _t}, \\ = \left[ \begin{array}{l} {\mathit{\boldsymbol{X}}_t}\mathit{\boldsymbol{\beta }} + \rho W{\mathit{\boldsymbol{y}}_{t - 1}} + {\mathit{\boldsymbol{\varepsilon }}_t}, 1 \le t < {a_1}, \\ {\mathit{\boldsymbol{X}}_t}\left( {\mathit{\boldsymbol{\beta }} + {\mathit{\boldsymbol{\delta }}_1}} \right) + \left( {\rho + {\rho _1}} \right)W{\mathit{\boldsymbol{y}}_{t - 1}} + {\mathit{\boldsymbol{\varepsilon }}_t}, {a_1} \le t < {a_2}, \\ \cdots \\ {\mathit{\boldsymbol{X}}_t}\left( {\mathit{\boldsymbol{\beta }} + \sum\limits_{l = 1}^s {{\mathit{\boldsymbol{\delta }}_l}} } \right) + \left( {\rho + \sum\limits_{l = 1}^s {{\rho _l}} } \right)W{\mathit{\boldsymbol{y}}_{t - 1}} + {\mathit{\boldsymbol{\varepsilon }}_t}, {a_s} < t \le T. \end{array} \right. \end{array} $

(2)

式中：y_t=(y_{1, t}，…，y_{n, t})^T为房价，t为时间，n代表小区的个数；空间权重矩阵W为n×n维下三角矩阵，用来刻画小区间的相邻关系；X_t=(x_{t, 1}，…，x_{t, q})是n×q维矩阵；β=(β₁, …, β_q)^T≠0是q维回归系数向量；s是变点的个数；a₁, …，a_s是变点的位置。δ_l=(δ_{1, l}，…，δ_{q, l})^T, ρ_l, l=1，…，s为在变点上回归系数和空间自回归系数的改变，ε₁，…, ε_t是随机效应。

1.3 变点的估计方法

这里参考Jin等^[14]的两阶段变点估计方法。本文的模型与它的区别在于：

1) Jin等的响应变量y是一维的，而我们的模型y是n维的；2)Jin等的线性模型并未包含空间自回归系数。这里n固定，当n=1且空间自回归系数为0时即为Jin等提出的模型，本文模型的变点估计理论部分可参考Jin等^[14]。

第1阶段(分段，区间估计)：将T时间切分为p_t+1段，其中p_t=[$\sqrt T $]，这里[x]定义为对x向上取整。选一个整数m满足：数据的第1段的时间长度为T－p_tm，其他p_t段的长度为m。因此第1段的时间区间为τ₁=[1，…，T－p_tm]，第j段的时间区间为τ_j=[T－(p_t－j+2)m+1，…，T－(p_t－j+1)m]，j=2，…，p_t+1。由Jin等^[14]的分析，每个区间段至多只包含1个变点。令a_j∈τ_kj, j=1，…，s, 即A={k₁，…，k_s}为变点所在的区间段的集合。令${\mathit{\boldsymbol{\widetilde X}}_t} = \left({{\mathit{\boldsymbol{X}}_t}, {\mathit{\boldsymbol{y}}_{t - 1}}} \right){\mathit{\boldsymbol{\widetilde X}}_{\left(1 \right)}} = {\left({{{\widetilde {{\mathit{\boldsymbol{X}}_1}}}^{\rm{T}}}, \ldots, {{\mathit{\boldsymbol{\widetilde X}}}_{T - {p_t}m}}^{\rm{T}}} \right)^{\rm{T}}}$，${\mathit{\boldsymbol{\widetilde X}}_{(j)}} = \left({{{\mathit{\boldsymbol{\widetilde X}}}_{T - \left({{p_t} - j + 2} \right)m + 1}}^{\rm{T}}, \ldots, {{\mathit{\boldsymbol{\widetilde X}}}_{T - \left({{p_t} - j + 1} \right)m + 1}}^{\rm{T}}} \right)$, j=2，…，p_t+1。${\mathit{\boldsymbol{\widetilde X}}^{(1)}} = {({\mathit{\boldsymbol{\widetilde X}}_1}^{\rm{T}}, {\mathit{\boldsymbol{\widetilde X}}_2}^{\rm{T}}, \ldots, {\mathit{\boldsymbol{\widetilde X}}_{({p_t} + 1)}}^{\rm{T}})^{\rm{T}}}$, ${\mathit{\boldsymbol{\widetilde X}}^{(j)}} = {({\rm{ }}{0_{q + 1 \times (T - \left({{p_t} - j + 2} \right)m)}}, {\mathit{\boldsymbol{\widetilde X}}_{(j)}}^{\rm{T}}, {\mathit{\boldsymbol{\widetilde X}}_{(j + 1)}}^{\rm{T}}, \ldots, {\mathit{\boldsymbol{\widetilde X}}_{({p_t} + 1)}}^{\rm{T}})^{\rm{T}}}$，j=2，…，p_t+1。与Jin等^[14]类似，扩展自变量矩阵为$\mathit{\boldsymbol{\widetilde X}} = ({\mathit{\boldsymbol{\widetilde X}}^{(1)}}, \ldots, {\mathit{\boldsymbol{\widetilde X}}^{({P_t} + 1)}})$, 因此$\mathit{\boldsymbol{\widetilde X}}$为nT×(q+1)(p_t+1)维矩阵。拉直因变量向量为$\mathit{\boldsymbol{\widetilde y}} = {({\rm{ }}{\mathit{\boldsymbol{y}}_1}^{\rm{T}}, \ldots, {\mathit{\boldsymbol{y}}_T}^{\rm{T}})^{\rm{T}}}$, 因此$\mathit{\boldsymbol{\widetilde y}}$为nT维向量，令θ=(θ₁^T, …, θ^T_pt+1)，其中θ_j为q+1维向量。采用Group Lasso求解回归系数θ：

$ \left.\hat{\boldsymbol{\theta}}=\underset{\theta \in R(q+1)\left(p_{t}+1\right)}{\arg \min \limits}\left(\|\tilde{\boldsymbol{y}}-\tilde{\boldsymbol{X}} \boldsymbol{\theta}\|_{2}^{2}+\lambda \sum\limits_{j=2}^{p_{t}+1}\left\|\boldsymbol{\theta}_{j}\right\|_{2}\right)\right). $

(3)

令$\hat{\boldsymbol{\theta}}=\left(\boldsymbol{\theta}_{1}^{\mathrm{T}}, \cdots, \boldsymbol{\theta}_{p_{\mathrm{t}+1}}^{\mathrm{T}}\right)^{\mathrm{T}}, \hat{A}=\left\{\hat{k}_{1}, \hat{k}_{2}, \cdots, \hat{k}_{\hat{s}}\right\}=\left\{k: \hat{{\theta}}_{k}\right.$≠0, k=2，…，p_t+1}, 采用BIC准则选取参数λ，则集合$\widehat A$为A的估计，即变点可能在的区间为$\boldsymbol{\tau}_{\hat{k}_{j}}, j=1, \cdots, \hat{s}, \hat{k}_{j} \in A$.

第2阶段(再搜索，点估计)：令T_j^(l)=T -(p-${\widehat k_j}$+2)m+1, T_j^(r)=T-(p-${\widehat k_j}$+1)m+1, j=1，…，$\mathit{\widehat s}$, 变点的估计可由下式的累计和方法得出：

$ \begin{array}{*{20}{c}} {{{\hat a}_j} = {\rm{arg}}\;\mathop {{\rm{min}}}\limits_{{T_j}^{(l)} < k < {T_j}^{(r)}} \left[ {\mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{\theta }} \sum\limits_{t = T_j^{(l)}}^k {{{\left( {{\mathit{\boldsymbol{y}}_t} - {{\mathit{\boldsymbol{\tilde X}}}_t}\mathit{\boldsymbol{\theta }}} \right)}^2}} + } \right.}\\ {\left. {\quad \mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{\theta }} \sum\limits_{t = k + 1}^{T_j^{(r)}} {{{\left( {{\mathit{\boldsymbol{y}}_t} - {{\mathit{\boldsymbol{\widetilde X}}}_t}\mathit{\boldsymbol{\theta }}} \right)}^2}} } \right],j = 1, \cdots ,\hat s.} \end{array} $

(4)

2 实证分析 2.1 数据来源和变量选取

本文选用合肥市2016年6月至2017年6月的在售普通商品住宅作为研究对象，样本数据来自中国房价网以及安居客，总共搜集246个小区每周的均价作为分析的数据基础。为保证可比性，将所有变量进行中心标准化

特征变量的量化与预期：

1) x1：小区物业价格。以住宅实际物业管理费用引入模型，单位为元。

2) x2：绿化率。以住宅实际绿化覆盖率引入模型，单位为%。

3) x3:总建筑面积。以住宅小区总的建筑面积引入模型，单位m³。

4) x4：容积率。以住宅小区总建筑面积和用地面积的比率引入模型，单位为%。

5) x5:小区竣工时间。2004年之前设为0, 2005—2006年设为1, 2007—2008年设为2，2009—2010年设为3，2011—2012年设为4, 2013年之后设为5。

6) x6：地铁。小区附近有地铁为1，没有为0。

7) x7:高铁站。小区离高铁站较近为1，较远为0。

8) x8:商业区。小区1 km内有商业区为1，没有为0。

9) x9:公园。小区1 km内有公园为1，没有为0。

10) x10:小学。附近小学在合肥市区排名前8名为1，其余为0。

11) x11:中学：附近中学在合肥市区排名前5名为1，其余为0。

2.2 空间格局分析

常用的点要素空间分布格局探测的方法是最近邻距离分析，用于判断点分布的空间分布格局。基本思路是：计算每个要素和与其最近邻要素之间的平均距离，根据平均距离计算其最近邻指数，最近邻指数是平均观测距离和平均期望距离的比值。如果最近邻指数小于1，则要素呈现空间集聚模式；如果大于1，则要素呈现空间离散模式或竞争模式。用最近邻域法对合肥市小区分布做聚集分析，使用ARCGIS中的平均最近邻分析工具，得到表 1。

由表 1可以看出，合肥市样本住宅的最近邻距离系数为0.813，该区域住宅楼呈集聚分布形态，Z检验值为-10.084(明显小于0.05显著水平下的Z值-1.96)，P等于0表示这种情况随机分布的概率很小。综上表明，合肥市的小区集聚特征十分显著。

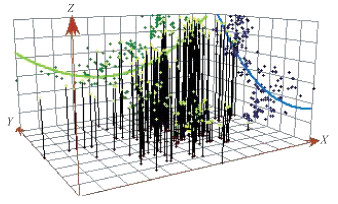
将住宅价格数据按照数值投影到水平和竖直的平面上，观察房价在东西以及南北方向上的变化趋势，得到如图 1趋势图。从图中看出，住宅价格均在X、Y方向上呈现抛物线变化，即存在二阶趋势。样本数据在Y轴方向上呈现出明显的倒U型趋势，表明在东西方向上有中心向边缘递减的趋势明显，呈现出较为复杂的二阶曲线形态，X轴上标明从房价北到南呈现逐渐递减的趋势。

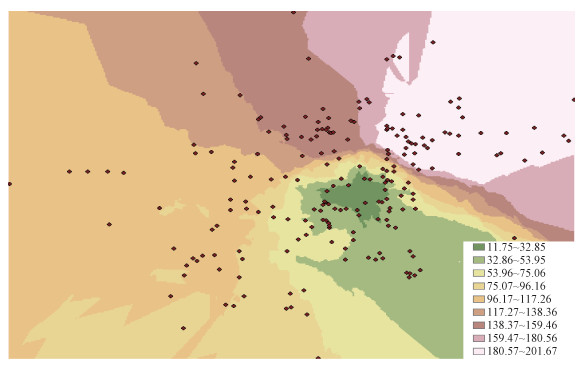
采用Kringing空间内插法住宅价格数据进行局部内插处理，生成连续的价格表面，如图 2所示。分析表明，住宅价格在东西方向上由中心向四周递减，在南北方向上从北到南逐渐递减，在衰减的同时，并未产生跳跃区域，空间变异性不明显。

2.3 空间自相关 2.3.1 全局空间自相关

在一定范围内，Moran’s I统计量显示合肥市住宅地价总体呈现显著的正自相关特征，不同的空间权重矩阵对自相关统计量的探测结果有显著影响，采用距离权重，从表 2可以看出，选取d=0.80 km时，空间自相关最显著，Moran’s I为0.421.

2.3.2 局部自相关

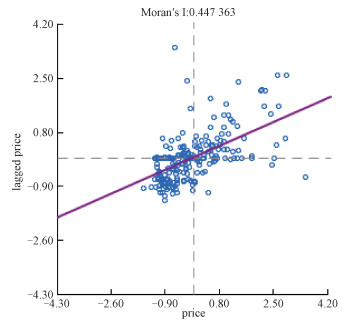
以合肥市部分住宅小区为例，采用Moran散点图(如图 3所示)分析住宅价格的局部相关性，用来揭示房价空间分布的异质性。Moran散点图用于研究局域空间的异质性，其横坐标是每个样本点房价的标准化值，纵坐标为空间权重矩阵所确定的相邻样点的属性值的平均值(经标准化处理)。其中第1象限为“高—高”，代表高观测值区域单元为同是高观测值区域所包围的空间关联形式，第2象限为“低—高”, 代表低观测值的区域单元为高观测值区域所包围的空间关联形式; 第3象限为“低—低”, 代表低观测值的区域单元为同是低观测站的区域所包围的空间关联形式; 第4象限为“高—低”, 代表高观测值的区域单元为低观测值的区域所包围的空间关联形式。从Moran散点图可以看出，住宅价格样本主要分布在第1象限和第3象限，其次是第2象限，说明房价空间关联性较为显著。

2.4 变点检测

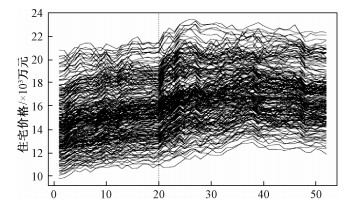
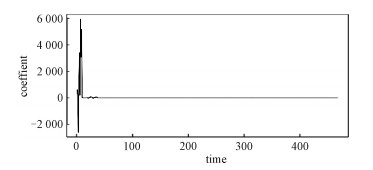
图 4为合肥市2016年6月到2017年6月样本点平均住宅价格。将住宅价格数据切分成52段，每段的长度为72，假设每段至多有1个变点。从图 5可以看出，在第20时间段内，系数的增量不为0，房价波动较大，存在变点, 后面的时间段系数的增量接近于0，由BIC的选取原则为：BIC=klogn－2nlog(RSS/n)(其中k为模型参数个数，n为样本个数)，得出BIC最小值为-14 828.036 4，对应的λ为0.382 7。由变点的估计方法得出在第20时间段存在变点，对应的时间为2016年10月31日。变点发生的时刻与合肥市2016年10月份发布的限购政策吻合。从而将数据分成两段，第1段为2016年6月20日到2016年10月31日，第2段为2016年11月7到2017年6月12日。

2.5 空间网络自回归模型

分别对两个时间段以及总时间段做空间网络自回归模型，在0.05的显著水平下，去掉不显著的变量，再建立模型。从表 3可以看出，x1(小区物业价格)、x2(绿化率)对住宅价格影响不显著。x3(总建筑面积)对住宅价格有正向影响，总建筑面积大的住宅价格偏高。x4(容积率)对住宅价格具有显著正向影响，容积率越高，住宅价格越高。x5(小区竣工时间)、x7(高铁站)对住宅价格没有显著的影响。x6(地铁)、x8(商业区)对住宅价格的影响较为显著，在地铁以及商业区附近的小区，价格相对更高。x9(公园)对住宅价格无显著影响。x10(重点小学)、x11(重点中学)对住宅价格的影响显著，重点中学附近的学区房，价格明显更高。

通过对比模型的检验结果(如表 4所示)发现，时间段1和时间段2的R²均达到0.5，高于总时间段。时间段1和时间段2的AIC准则以及SC准则低于总时间段，而Loglike-hood高于总时间段。时间段1和时间段2的模型拟合效果更好，说明变点对空间模型有一定的影响，按照变点对数据进行划分再分别进行空间分析效果更好。

3 结论与讨论

本文以合肥市为研究区域，研究住宅价格的分布及其影响因素，结果表明：

1) 通过对样本房价空间自相关的检测，在选取适当的权重矩阵下，全局自相关系数为0.421, 表明合肥市住宅价格有较强的空间依赖性，受周边住宅价格低影响较大。同时其空间分布呈现出“高—高”、“低—低”的集聚特征，由此说明城市住宅价格的形成在空间上存在关联，空间分布格局受到空间效应的影响。通过对住宅价格进行趋势分析以及克里金插值分析，发现价格呈现从中心向四周递减的趋势，房价最高的地区在万达广场附近。

2) 变点在第20个时间段其他时间段房价趋于平稳，分析原因可能是：第20个时间段对应的时间为2016年10月31日，而10月1号合肥市政府推出限购政策，导致房价变化较大。通过对比模型的检验结果，发现分别建立空间滞后模型的效果更好，时间段1以及时间段2的模型拟合度比总时间段的模型拟合更好。说明找出房价数据的变点，去掉房价较大波动的影响后，再分析房价的影响因素，结果更为可靠。

3) 除空间因素外，总建筑面积和容积率对住宅价格的影响显著，说明住宅价格受到住宅条件的影响。地铁、商业区、重点小学、重点中学对住宅价格的影响较为显著，说明区位对住宅价格影响较大，基础教育设施、生活配套设施越完善，房价越高。