2. 中国科学院大学, 北京 100049;
3. 上海科技大学信息学院, 上海 201210
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. School of Information Science & Technology, ShanghaiTech University, Shanghai 201210, China
随着无线电通信技术的快速发展,无线频谱资源日益紧张, 认知无线电(cognitive radio, CR)[1-2]成为解决此问题的关键技术之一。频谱感知不仅包括精确检测到授权用户(primary user, PU)的通信信号,同时还可以精确识别其调制类型,进而可以确定授权用户的业务类别等先验信息,从而利用这些信息使认知用户(cognitive user, CU)更有效地发现和使用空闲频谱,提高频谱利用率。
频谱感知是CR的首要特征和核心部分,经典的感知算法[3]包括能量检测算法、循环平稳特征检测算法、匹配滤波器检测算法等。能量检测算法结构简单,不需要PU发射机信号的先验知识,但是易受到噪声的影响,门限不易确定。循环平稳特征检测法抵抗噪声能力强,但是检测时间长,适用性差。匹配滤波器检测法需要PU发射机信号的波形,频段等先验知识,且对同步要求高,在实际场景中难以满足。
移动无线通信中,由于存在多径效应、隐藏节点等问题,造成单个CU的感知精确度难以达到要求,而合作频谱感知可以在低信噪比下显著提高检测效率及可靠性,并可以解决隐藏节点问题。文献[4]充分考虑信号的多径衰落以及阴影效应,提出一种基于能量的合作频谱感知方法,此算法提高了频谱感知效率和可信度,克服了隐藏节点带来的问题,但是仍然受到噪声的影响。文献[5]提出一种基于支持向量机(support vector machine, SVM)的频谱感知算法,利用循环频谱特征值作为信号的特征,通过SVM分类器实现频谱感知,但是此算法计算复杂度较高,而且在训练大规模频谱数据的时候,容易出现过拟合情况,直接影响感知效果。为了避免过拟合情况,文献[6]提出一种基于随机森林的频谱感知算法,此算法从CU接受到的信号中提取能量最大的信号循环谱中特征参数,并以此作为随机森林的训练特征值。此算法带来了一定性能上的提升,但是在计算能量值过程中易受到平滑样本数数值的影响。文献[7]提出一种将能量值与神经网络结合(energy detection with neural network, EDNN)的合作频谱感知算法,此算法将多个CU接收到的信号能量值作为信号的特征参数,通过神经网络实现频谱感知功能。此算法利用神经网络在分类中的优势和合作频谱感知的优势,提高了低信噪比情况下的检测概率和可信度。
信号调制类型识别研究方法主要分为应用假设检验理论实现信号调制类型识别和模式识别方法。前者计算量大且不易实现,而模式识别方法主要是利用特征提取方法提取特征后通过分类器进行识别[8],常用的特征有瞬时振幅与相位、频谱特征、高阶累积量等。由于不同调制信号的特征值存在差异,因此分类器通过特征值识别不同的调制信号。文献[9-10]提出一种基于高阶统计量和频谱特征与SVM的信号识别方法,但是单个的SVM难以实现多个调制类型的分类,因此需要多个SVM实现多种调制信号识别,增大了系统实现多种调制类型识别的复杂度。
本文提出一种基于神经网络的合作频谱感知算法,将其极大-极小特征值的比值和平均-最小特征值的比值[11-12]以及每个CU接收到信号的高阶统计量作为信号的特征参数,通过神经网络实现合作频谱感知。该算法不需要提前设定门限值,并可以在个别参数失真的情况下保证整体的感知效果。仿真实验首先对本文算法、ED合作检测算法与ED-NN算法的频谱检测概率和虚警概率进行比较,并对该算法对不同调制信号类型的识别率做了比较分析,之后对本文算法和ED-NN算法在不同CU数目下的频谱检测概率及虚警概率进行比较,并对本算法在不同CU数目下信号调制类型的平均识别率做了比较分析。仿真结果显示,在低信噪比的情况下,本文算法频谱检测准确率高于其他算法,且对信号调制类型有很高的识别率。其次,CU数目的增加会提高频谱检测准确率,本算法在CU数目为5时检测性能同ED-NN算法在CU数目为10的检测性能相近,同时可以提高系统对各调制类型信号的识别率。
1 系统模型假设认知网络中存在一个PU,M个CU独立接收PU发射机信号。频谱感知中的频谱检测可以作为一个二分类问题, 即可以用H0表示频谱空闲,即PU信号不存在,H1表示频谱占用,PU信号存在。合作频谱感知网络中每一个CU接收到的信号可表示如下:
| $ \boldsymbol{x}_{i}(n)=\left\{\begin{array}{ll} w_{i}(n), & H_{0}, \\ \bar{s}_{i}(n)+w_{i}(n), & H_{1}. \end{array}\right. $ | (1) |
式中:xi(n)为第i个CU接收到的信号;wi(n)是均值为0,方差为σw2的独立同分布高斯白噪声;si(n)是感知用户接收到经过路径损耗及多径衰落后的信号,实际环境中si(n)中可能为多个PU信号的叠加,此时假设只有一个PU信号,且信号和噪声互不相关,则si(n)=hi(n)s(n),s(n)为PU发射机发送的信号,hi(n)表示当前时刻下PU与第i个CU之间的信道增益,考虑到实际通信环境中的衰落情况,文中假设hi(n)服从瑞利分布。
假设每个CU在感知周期中的信号样本点数目为N,融合中心中M个CU接收到的信号可以表示为X=[x1, x2,…,xM]T,同理可得到S=
| $ \boldsymbol{X}=\left[\begin{array}{c} \boldsymbol{x}_{1} \\ \boldsymbol{x}_{2} \\ \vdots \\ \boldsymbol{x}_{M} \end{array}\right]=\left[\begin{array}{cccc} x_{1}(1) & x_{1}(2) & \dots & x_{1}(N) \\ x_{2}(1) & x_{2}(1) & \dots & x_{2}(N) \\ \vdots & \vdots & \vdots & \vdots \\ x_{M}(1) & x_{M}(2) & \dots & x_{M}(N) \end{array}\right]. $ | (2) |
同理,矩阵S与W也为M×N的矩阵。本算法用于实现频谱感知的信号特征参数均从接受的信号矩阵X提取。
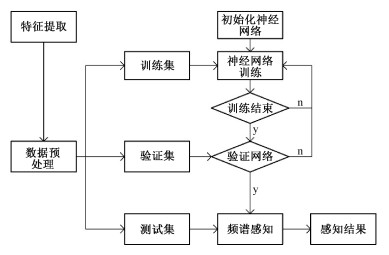
神经网络实现频谱感知的流程如图 1所示。由于实时通信过程中通信数据比较大,因此首先将数据进行特征提取以降低数据的输入维度,之后将对特征数据处理后将数据按比例随机分为训练集、验证集、测试集,将训练集的特征数据输入到已经初始化的神经网络中进行训练,当网络的训练误差小于预设阈值或达到最大训练迭代次数时则停止网络训练,之后通过验证集的特征数据对神经网络性能进行验证,选择泛化性能最好的神经网络,最后将测试集的特征数据输入泛化能力最好的神经网络对算法的性能进行测试。
|
Download:
|
| 图 1 神经网络频谱感知流程图 Fig. 1 Flowchart of neural network based spectrum sensing | |
1) 最大-最小特征值比值与平均-最小特征值比值假设融合中心对接收到的信号进行采样,在每个感知周期中采样的个数为N。首先计算矩阵X、S、W的协方差矩阵。
| $ \begin{aligned} {\boldsymbol{R}_\boldsymbol{X}} &=E\left(\boldsymbol{X} \boldsymbol{X}^{\mathrm{H}}\right) , \end{aligned} $ | (3) |
| $ \begin{aligned} {\boldsymbol{R}_\boldsymbol{S}} &=E\left(\boldsymbol{S S}^{\mathrm{H}}\right) , \end{aligned} $ | (4) |
| $\begin{aligned} {\boldsymbol{R}_\boldsymbol{W}} &=E\left(\boldsymbol{W W}^{\mathrm{H}}\right). \end{aligned} $ | (5) |
且由矩阵的运算可以得到
| $ {\mathit{\boldsymbol{R}}_\mathit{\boldsymbol{X}}} = {\mathit{\boldsymbol{R}}_\mathit{\boldsymbol{S}}} + {\mathit{\boldsymbol{R}}_\mathit{\boldsymbol{W}}} = {\mathit{\boldsymbol{R}}_\mathit{\boldsymbol{S}}} + \sigma _w^2{\mathit{\boldsymbol{I}}_{MM}}. $ | (6) |
式中:H表示矩阵的共轭转置,IMM为M × M的单位矩阵。由于在实际中只能获得有限采样点的信号样本,因此用样本矩阵的协方差矩阵RX(N)代替统计协方差矩阵来计算协方差矩阵,即
| $ {\boldsymbol{R}_{X}}={\boldsymbol{R}_{X}}(N)=\frac{1}{N} \sum\limits_{n=1}^{N} \boldsymbol{X} \boldsymbol{X}^{\mathrm{H}}. $ | (7) |
计算RX的最大特征值、最小特征值以及特征值的平均值,并且标为λmax,λmin,λave。则用于神经网络频谱检测的特征参数为β1=
2) 高阶统计量
本文主要对BPSK、QPSK、16QAM、64QAM这4种数字信号进行调制类型识别,文中对调制类型的识别采用高阶累积量作为特征值。首先定义信号x的P阶混合矩为
| $ M_{p q}=E\left[\boldsymbol{x}^{p-q}\left(\boldsymbol{x}^{*}\right)^{q}\right]. $ | (8) |
则此时信号x的高阶统计量定义为:
| $ C_{20}={cum}(\boldsymbol{x}, \boldsymbol{x})=M_{20}. $ | (9) |
| $ C_{21}={cum}\left(\boldsymbol{x}, \boldsymbol{x}^{*}\right)=M_{21} . $ | (10) |
| $ C_{40}={cum}(\boldsymbol{x}, \boldsymbol{x}, \boldsymbol{x}, \boldsymbol{x})=M_{40}-3 M_{20}^{2} . $ | (11) |
| $ C_{41}={cum}\left(\boldsymbol{x}, \boldsymbol{x}, \boldsymbol{x}, \boldsymbol{x}^{*}\right)=M_{41}-3 M_{20} M_{21}. $ | (12) |
| $ C_{42}={cum}\left(\boldsymbol{x}, \boldsymbol{x}, \boldsymbol{x}^{*}, \boldsymbol{x}^{*}\right)=M_{42}-\left|M_{20}\right|^{2}-2 M_{21}^{2}. $ | (13) |
| $ \begin{array}{c} C_{60}={cum}(\boldsymbol{x}, \boldsymbol{x}, \boldsymbol{x}, \boldsymbol{x}, \boldsymbol{x}, \boldsymbol{x}) \\ C_{60}=M_{60}-15 M_{20} M_{40}+30 M_{20}^{3}. \end{array} $ | (14) |
上述式子中的信号向量x为感知周期内各个CU接收到的PU发射机信号,即矩阵X的每一个行向量。对于信号向量xi(1 < i < M),4阶以上的高阶统计量不但可以减少噪声对通信信号带来的影响,而且可以反映不同调制信号的统计信息之间的差别,因此本文选择高阶统计量作为调制类型的识别的特征参数。
2.2 特征的理论分析(1) 特征值之比分析
假设RX的特征值为λ1≥λ2≥…≥λmin, RS的特征值为ρ1≥ρ2≥…≥ρmin,而RW的特征值为σw2,则根据公式(6)可得λn=ρn+σw2,假设在PU发射机无通信信号,即H0的状态下,此时S=0,则RS=0,则ρ1=ρ2=…=ρmin=0,所以此时λ1=λ2=…=λmin=σw2,此时可得λ1/λmin=1。如果存在PU信号,即H1情况下,则ρ1>ρmin,此时λ1/λmin>1。因此在频谱感知的过程中,特征量λ1/λmin在PU发射机在通信和未通信的情况中存在较大的区别,因此神经网络可以通过判断λ1/λmin的比值确定PU发射机的通信状态。但是如果RS的特征值相同,即RS=λIMM,此时ρ1=ρ2=…=ρmin=λ,特征量β1=λ1/λmin=1=σw2/σw2,则神经网络不能通过此特征确定PU发射机的通信状态,但这种情况只发生在CU数M=1的情况,且要求信道为平坦衰落[11], 与本文的合作频谱感知条件不符,故不做考虑。
同理,假设λave为RX特征值的均值,若在H0的情况下,有S=0,则RS=0,ρ1=ρ2=…=ρmin=0,此时λave=λ1=λ2=…=λmin=σw2,此时λave/λmin=1。若在H1情况下,则λave>σw2, 此时有λave/λmin>1。故λave/λmin与λmax/λmin共同用作频谱检测的特征参数。
2) 高阶统计量分析
表 1所示为MPSK与MQAM的高阶累积量的信息,其中E为信号码元的能量。可以看出4种不同调制信号的二阶统计量C21相同,而高阶统计量C40和C42在数值上存在明显差异,因此可以作为区分BPSK、QPSK、16QAM、64QAM调制类型的特征参数。
|
|
表 1 MPSK和MQAM的高阶统计量信息 Table 1 Higher-order cumulants of MPAK and MQAM |
BP神经网络是一种按照误差逆向传播算法训练的多层前馈神经网络,其结构简单,性能稳定,而且在模式识别及多分类应用中有着出色的表现,3层BP神经网络包括输入层、隐藏层以及输出层,其结构如图 2所示。

|
Download:
|
| 图 2 BP神经网络的结构图 Fig. 2 BP-neural network structure | |
假设神经网络的输入层、隐藏层以及输出层分别有数目为L、P、Q的神经元,wni(1)为第n个输入神经元与第i个隐藏神经元之间的权重,wij(2)为第i个隐藏神经元与第j个输出神经元之间的权重,bi(k)为第i个神经元的阈值,其中上角标k为神经元的层数,k=1表示隐藏层,k=2表示为输出层。激活函数f1和f2为Sigmoid函数,Sigmoid函数表达式为
| $ \operatorname{Sigmoid}(x)=\frac{1}{1+\mathrm{e}^{-x}}. $ | (15) |
则隐藏层的第i个神经元输入αi与输出outi可以表示为:
| $ \begin{aligned} \alpha_{i} &=\sum\limits_{n=1}^{L} w_{n i}^{(1)} x_{n} . \end{aligned} $ | (16) |
| $ \begin{aligned} \text { out }_{i} &=f_{1}\left(\alpha_{i}+b_{i}^{(1)}\right). \end{aligned} $ | (17) |
则输出层的第j个神经元的输入βj与输出
| $ \begin{aligned} \beta_{j} &=\sum\limits_{i=1}^{P} w_{i j}^{(2)} \text { out }_{i}. \end{aligned} $ | (18) |
| $ \check{\boldsymbol{y}}(j) =f_{2}\left(\beta_{j}+b_{j}^{(2)}\right). $ | (19) |
神经网络的训练采用BP算法,根据误差信息对模型参数的修正。则根据如上的公式,此神经网络待学习的参数为
| $ \begin{aligned} \boldsymbol{\theta}=[\boldsymbol{w}, \boldsymbol{b}]=\left[w_{11}^{(1)}, w_{12}^{(1)} \cdots w_{1 P}^{(1)} \cdots w_{L 1}^{(1)} \cdots w_{L P}^{(1)}, w_{11}^{(2)}\right., \\ \left.w_{12}^{(2)}, \cdots, w_{P 1}^{(2)} \cdots w_{P Q}^{(2)}, b_{1}^{(1)}, \cdots b_{P}^{(1)}, b_{1}^{(2)}, \cdots b_{Q}^{(2)}\right] \end{aligned} $ |
此时,得到的优化目标函数(即误差函数)为
| $ C=\frac{1}{m} \sum\limits_{k=1}^{m}\left\|\check{\boldsymbol{y}}_{k}-\boldsymbol{y}_{k}\right\|_{2}^{2}+\frac{\lambda}{2 m} \boldsymbol{R}(\boldsymbol{\theta})=C_{0}+\frac{\lambda}{2 m} \boldsymbol{R}(\boldsymbol{\theta}). $ | (20) |
式中:R(θ)为正则项,可以有效避免神经网络在训练过程中陷入局部最优解,其中m为训练样本的数量,λ为正则化参数,用于调整正则项R(θ)与惩罚函数C0之间的关系。定义本文中的R(θ)=||w||22,其中向量yk为预先标记的对于当前频谱是否占用及4种信号调制类型的类别信息,因此其为一个包含5个参数的列向量,第1个参数对应于频谱检测的结果,存在PU发射机信号则为1,否则为0, 其余4个参数分别对应文中提及的4种调制类型,如果为对应信号则输出为1,否则为0,
| $ \begin{aligned} \Delta w_{i j}^{(k)}=-\eta \frac{\partial C}{\partial w_{i j}^{(k)}} &=-\eta\left(\frac{\partial C_{0}}{\partial w_{i j}^{(k)}}+\frac{\lambda}{m} w_{i j}^{(k)}\right) , \end{aligned} $ | (21) |
| $ \begin{aligned} \Delta b_{i}^{(k)}=&-\eta \frac{\partial C}{\partial b_{i}^{(k)}}=-\eta \frac{\partial C_{0}}{\partial b_{i}^{(k)}}. \end{aligned} $ | (22) |
由此可以得到神经网络中的权值更新公式为
| $ P=\sqrt{L+Q}+\varphi, $ | (23) |
式中φ取1~10之间的数,并在此范围逐一选取隐藏层节点个数进行训练,根据性能选择最佳节点个数。
3 算法流程综上所述,本文基于特征值分布的神经网络频谱感知算法的步骤如下:
步骤1:根据融合中心接收到的信号计算用于频谱感知的特征值β1、β2,以及各CU接收信号的4阶统计量C40和C42。
步骤2:初始化神经网络的权重参数w和各神经元阈值b,并且设定神经网络的终止条件,即训练误差的阈值及最大训练次数。
步骤3:将数据随机分为训练集、验证集、测试集,将训练集的特征值输入神经网络,根据式(16)~式(22)进行训练,当神经网络训练误差小于预先设定的误差阈值或者达到最大训练次数时停止训练。
步骤4:将验证集输入步骤3训练好的神经网络,判断其是否存在过拟合, 并根据网络的表现情况调整神经网络。
步骤5:根据验证集验证之后返回最佳的神经网络参数,并通过测试集对训练完成的神经网络进行性能测试。
4 仿真结果及分析为验证本文算法的有效性,在Matlab下进行仿真验证,共10 000组数据,BPSK、QPSK、16QAM、64QAM信号各2 500组,将随机选取各种调制信号的40%数据组成训练集,30%组成验证集,30%组成测试集。假定感知网络中只有一个PU进行通信,多个CU对该频谱进行合作频谱感知,所有用户在感知期间的位置不变,且PU与CU之间存在瑞利衰减信道。设定公式(20)误差函数中正则项参数λ=0.5,式(21)、式(22)中学习速率η=0.1,并且设定神经网络的误差阈值为10-4,最大迭代次数为103。
基于以上场景本文仿真了两种情况,首先比较当CU用户数M=5时,给定不同的信噪比,ED检测算法、EDNN检测算法和本文提出的神经网络检测算法的性能。由于ED检测算法在实际中容易出现对噪声估计的不确定性,因此ED-x dB表示ED检测算法中噪声的不确定度的上限为x dB,假设估计的噪声方差为
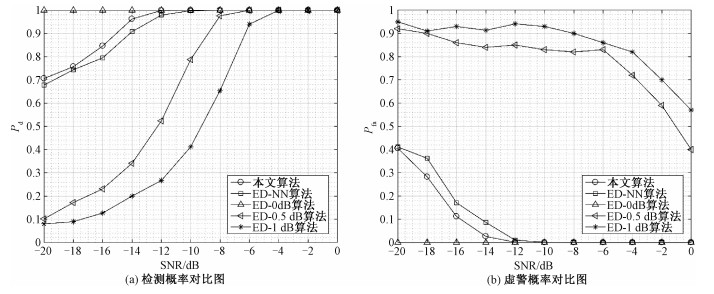
图 3(a)为不同算法的频谱检测概率Pd随信噪比SNR变化的特性曲线图。由于ED检测算法需要提前假设虚警概率来确定检测时候的门限值,为保证检测的准确性,假设Pfa=0.1。由图可知,如果噪声的方差可以精确估计,ED-0 dB算法均表现最优。当SNR=-20 dB时,本文提出算法的Pd可以达到71%,ED-NN算法可以达到67%,而此时ED-0.5 dB和ED-1 dB的Pd仅分别为10%和8%,而在SNR=-12 dB的时候本文提出算法的检测效率可以达到99%,ED-NN可以达到95%,但是ED-0.5 dB和ED-1 dB的Pd仅分别为52%和32%。因此在实际的检测环境中传统的能量检测算法由于对噪声方差估计的不确定性,检测性能远远低于本文提出的算法以及ED-NN算法。
|
Download:
|
| 图 3 不同算法的检测性能对比图 Fig. 3 Comparison of detection performance among different algorithms | |
图 3(b)是不同算法实际中的Pfa随SNR变化的曲线,ED检测算法都是假设Pfa=0.1的前提下所测得的实际Pfa。由图可知,ED-0 dB的表现最优,其Pfa为0,但是ED-xdB情况下的实际虚警概率是远远高于0.1的,可以看出,在SNR=-20 dB的情况下,本文提出的算法Pfa为42%,而EDNN算法的Pfa为41%,而ED-0.5 dB和ED-1 dB的实际Pfa达到89%和92%。而在SNR=-16 dB时,本文算法的Pfa为11%,而EDNN算法则为17%,ED-0.5 dB和ED-1 dB为89%和92%。当SNR=-12 dB时,本文算法和ED-NN算法的虚警概率降到0.7%和1%。因此本文算法在相同条件下的表现远远优于ED合作频谱感知,而且相对于ED-NN算法也有了一定的性能增益,可提供更加可靠的频谱检测性能。
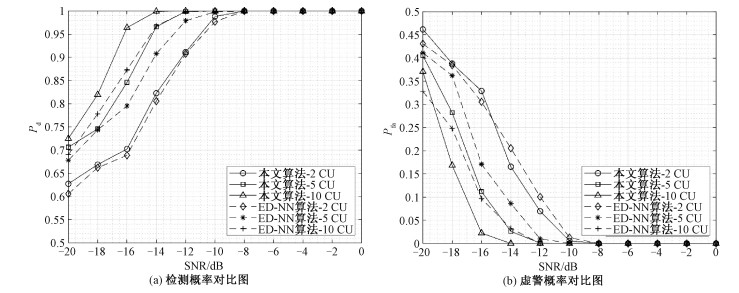
图 4(a)是不同CU数目M情况下EDNN算法和本文算法的频谱检测概率Pd的对比图,此时选取M的值为2、5、10。在M=2时,2种算法的检测效果十分接近。当M=5时,本文算法在SNR=-12 dB时Pd可以达到99%,而EDNN算法在SNR=-10 dB时才可以达到99%。当M=10时,本文算法在SNR=-14 dB时Pd可以达到99%,而EDNN算法在SNR=-12 dB时才能达到99%。同时可以看到本文算法在M=5时的Pd跟ED-NN算法M=10的Pd相近。因此本文算法可以用较少的CU达到更好的频谱检测效果,提高实际环境中的频谱利用率。
|
Download:
|
| 图 4 感知用户数目对检测性能的影响 Fig. 4 Impact of number of cognitive users on detection performance | |
图 4(b)是不同CU数目M情况下EDNN算法和本文算法的频谱检测虚警概率Pfa对比图。在M=2时,2种算法的Pfa十分接近。当M=5时,本文算法相比EDNN算法的Pfa显著降低,当SNR=-18 dB时,本文算法的Pfa为27%,而EDNN算法的Pfa为37%,在SNR=-16 dB时,本文算法的Pfa只有11%,而EDNN算法的Pfa为31%。当M=10,在SNR=-18 dB时,本文算法的Pfa为17%,而EDNN算法的Pfa为25%,当SNR=-16 dB时,本文算法的Pfa为2%,而EDNN算法的Pfa为10%。同时,可以看到在SNR大于-18 dB时,本文算法在M=5时的性能同EDNN算法在M=10时的性能十分接近。结合图 4(a)所示,可知在实际的检测环境中,本文算法可以在相同CU数目下提供更加可靠的频谱检测性能。
表 2是在认知网络中,CU数目为2、5、10时在不同SNR情况下对4种调制信号的识别率对比表。
|
|
表 2 信号调制类别检测结果
Table 2 Result of signal modulation classification |
可以看出,4种信号调制类型的识别率随着CU数目增加而提高。当SNR=-4 dB,M=2的平均识别率为79.9%,M=5的平均识别率为87.3%,而M=10的平均识别率可以达到90.1%。而在SNR=0 dB时,3种不同CU数目下的系统的平均识别率分别达到90.6%、93.9%和95.3%。同时,由于16QAM与64QAM信号的高阶统计量C40与C42非常接近,系统在各情况下对16QAM与64QAM信号识别的准确率要低于BPSK与QPSK,因此在实际中可以通过增加CU的数目提高16QAM及64QAM调制信号的识别率。
5 结束语合作频谱感知可以有效地提高频谱感知的准确性,而传统的合作频谱感知方式需要PU信号和信道的先验知识。本文提出基于神经网络的盲频谱感知算法,利用神经网络在多分类问题中不需要提前设定门限值,且具有自适应学习的优势。将最大-最小特征值之比、平均-最小特征值之比以及高阶统计量作为输入神经网络的特征参数实现频谱感知。仿真表明,本算法较其他算法不仅在低信噪比情况下有着较好的频谱检测性能,而且可以通过同一个神经网络同时实现对PU发射机信号调制类型的识别,帮助CR系统实现更加准确高效的频谱管理。但是本文算法对16QAM及64QAM调制信号在低SNR下识别准确度比较低,后续可对高阶QAM调制信号的其他特征参数做研究以提高算法对高阶调制信号识别的性能。
| [1] |
Haykin S. Cognitive radio:brain-empowered[J]. IEEE Journal on Selected Areas in Communications, 2005, 23(2): 201-220. Doi:10.1109/JSAC.2004.839380 |
| [2] |
Jiang C X, Zhang H J, Ren Y, et al. Machine learning paradigms for next-generation wireless networks[J]. IEEE Wireless Communications, 2017, 24(2): 98-105. Doi:10.1109/MWC.2016.1500356WC |
| [3] |
Khan A A, Rehmani M H, Reisslein M. Cognitive radio for smart grids:survey of architectures, spectrum sensing mechanisms, and networking protocols[J]. IEEE Communications Surveys and Tutorials, 2016, 18(1): 860-898. Doi:10.1109/COMST.2015.2481722 |
| [4] |
Atapattu S, Tellambura C. Energy detection based cooperative spectrum sensing in cognitive radio networks[J]. IEEE Transactions on Wireless Communications, 2010, 8(12): 5761-5766. |
| [5] |
Awe O P, Zhu Z M, Lambotharan S. Eigenvalue and support vector machine techniques for spectrum sensing in cognitive radio networks[C]//The 2013 Conference on Technologies and Applications of Artificial Intelligence(TAAI). Taipei: IEEE Press, 2013: 223-227.
|
| [6] |
王鑫, 汪晋宽, 刘志刚, 等. 基于随机森林的认知网络频谱感知算法[J]. 仪器仪表学报, 2013, 34(11): 2471-2488. |
| [7] |
Tang Y J, Zhang Q Y, Lin W. Artificial neural network based spectrum sensing method for cognitive radio[C]//6th International Conference on Wireless Communications Networking and Mobile Computing (WiCOM). Chengdu: IEEE Press, 2010: 1-4.
|
| [8] |
赵春晖, 杨伟超, 马爽. 基于广义二阶循环统计量的通信信号调制识别研究[J]. 通信学报, 2011, 32(1): 144-150. Doi:10.3969/j.issn.1000-436X.2011.01.019 |
| [9] |
刘明骞, 李兵兵, 曹超凤, 等. 认知无线电中非高斯噪声下数字调制信号识别方法[J]. 通信学报, 2014, 35(1): 82-88. Doi:10.3969/j.issn.1000-436x.2014.01.010 |
| [10] |
Yang F, Li Z, Zeng S. A novel method for wireless communication signal modulation recognition in smart grid[J]. Journal of Communications, 2016, 11(9): 813-818. |
| [11] |
Zeng Y H, Liang Y C. Eigenvalue-based spectrum sensing algorithms for cognitive radio[J]. IEEE Transactions on Communications, 2009, 57(6): 1784-1793. Doi:10.1109/TCOMM.2009.06.070402 |
| [12] |
弥寅, 卢光跃. 基于特征值极限分布的合作频谱感知[J]. 通信学报, 2015, 36(1): 84-89. |
 2020, Vol. 37
2020, Vol. 37 


