热液型矿床作为一种重要的矿床类型,一般产于碰撞造山带环境或拉伸环境,该类型矿床在中国分布广泛[1]。20世纪80年代,曾庆丰[2]及宋焕斌和戴福盛[3]已对热液型矿床进行系统的研究分析,并将其划分为岩浆热液矿床、再造热液矿床、变质和混合岩化热液矿床等。其中,岩浆热液型矿床包括大部分的有色金属矿产(Au、Cu、Mo和Sn等)及稀有元素矿产等矿种。金矿是一种贵重金属,因此,岩浆热液型金矿自然成为学者的重点研究对象。Hedenquist和Lowenstern[4]研究发现岩浆在热液金矿床形成中有重要作用,岩浆最重要的意义在于它是流体赖以上升的场所,是流体循环、上升、富集游离金元素的场所。曾庆丰[5]对矿液运移问题的研究发现断裂等构造是矿液运移的主要渠道也是矿石储集的区域。同时,Hustonl[6]通过对成矿热液的进一步研究发现温度、压力、pH值、盐度、氧化还原和硫含量等因素是金矿形成的重要影响因素。由上可知,岩浆热液型金矿的形成主要受流体压力、温度和构造等控制。目前,对岩浆热液型金矿床的温度、压力的研究通常以对流体包裹体的研究为主,以此确定金矿形成时的温度和压力[7-8]。例如,张德会等[9]研究岩浆热液成矿深度的主要影响因素,并提出使用流体包裹体进行成矿深度的估算方法。陈柏林[10]提出运用流体包裹体压力对受韧脆性转换带、高角度逆断层控制的脉状金矿床成矿深度的估算方法。另外,对影响矿床构造的研究现侧重于野外观测、测量及室内实验分析[11]。例如,安芳和朱永峰[12]对岩浆热液成矿的地球化学问题进行研究分析。
随着计算机技术的快速发展,数值模拟方法也被广泛运用于热液矿床的研究中。例如,Gamal和Piotr[13]对二维流体在多孔介质中流动和传热进行数值分析。Zhang等[14]采用二维数值模型对金矿床进行分析,确定金矿的形成与断层有关。Zhao等[15]用有限元数值模拟方法实现流体孔隙、热传递和成矿作用之间的耦合问题,并进一步预测可能的成矿区。张嵩松[16]对岩浆热液成矿系统的热场和流场分别进行数值模拟,进一步分析成矿区温度和压力的演化过程及对金矿成矿的影响。李正君[17]采用数值计算方法分析岩浆热液系统温度场和流体场的演化过程,并讨论断裂对成矿的影响。近年来,热液成矿瞬态数值分析也逐渐增多。例如,Liu等[18-19]对成矿热液流体进行短时间的瞬态数值分析;Xing[20]尝试复杂断裂系统中瞬态流体流动和传热的非线性有限元分析;Ingebritsen和Appold[21]给出水热系统的基本原理,并对岩浆热液成矿系统渗透率动态变化进行数值分析。如今,热液成矿数值模拟技术逐渐成熟,进一步加深了对岩浆热液成矿系统的了解。据此,本文以熊耳山前河地区金矿为例,结合已有的地质背景资料和前人对成矿深度的相关研究、估算成矿深度,运用有限元数值计算方法(COMSOL多物理场数值模拟软件),结合区域地质背景资料,搭建区域地质模型。在对成矿稳态模拟的基础上获得与实际成矿情况吻合的温压条件,并探讨成矿断裂带宽度、底部压力和渗透系数等对计算结果的影响。最后,采用瞬态数值模拟的方法进一步分析成矿过程中温度场和压力场的动态变化,以期进一步探讨金矿形成时的地质环境背景。
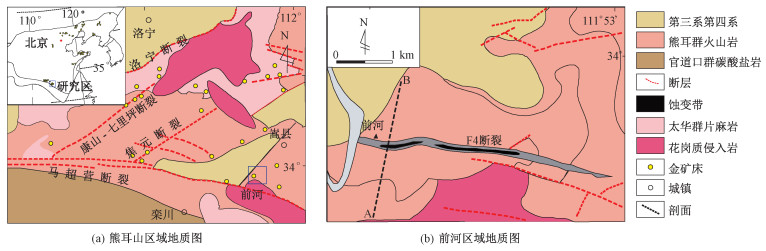
1 地质背景概况熊耳山地区位于华北克拉通南缘,秦岭造山带的北缘。该地区主要地层有太古界太华群、中元古界熊耳群、中—新元古界官道口群和中—新元古界栾川群,见图 1(a)[22]。朱日祥等[23]对华北克拉通的金矿进行研究,发现秦岭地区金矿主要形成于早中生代燕山期和早中生代印支期,主要赋矿岩层为太古界太华群片麻岩和中元古界熊耳群火山岩。在早中生代燕山期成矿时早白垩世发生了大规模岩浆活动,而在印支期成矿时在秦岭造山带发生陆陆碰撞,这说明主要成岩成矿事件与华北克拉通破坏峰期同时或准同时。前人研究得出金矿主要受断裂构造控制,且矿体主要赋存于断裂构造的次级断裂带中[24-25]。熊耳山地区主要断裂有马超营断裂、洛宁山前断裂、康山—七里坪断裂、焦元断裂[22]。
|
Download:
|
| 图 1 熊耳山前河地区地质图(据唐克非[22],朱日祥等[23],有改动) Fig. 1 Geological map of the Qianhe region in Xiong'ershan(modified from Refs.[22-23]) | |
前河金矿是熊耳山地区具有代表性的热液型金矿。该金矿是典型的构造蚀变岩型金矿,主要赋矿岩体为中元古界熊耳群安山岩,且矿体于地表出露,见图 1(b)。该区成矿物质来源以深部幔源为主,成矿流体来源以岩浆热液为主[24-25]。吴发富[26]和刘永春[27]对流体包裹体分析,估测出该区成矿时间为(134.7±0.6)~(123.8±1.3) Ma,为早中生代燕山期。朱沛云等[28]研究认为成矿温度约为210~330 ℃。马超营大断裂带及其次级断裂(F4)构成该矿床主要的导矿和容矿构造[27]。
马超营断裂是熊耳山地区的主要断裂构造之一,由多条平行或分支断裂组成[29-30],总长约200 km,宽数十至数百米,深34~38 km。该断裂整体上走向100°~120°,倾角50°~80°。其中次级断裂F4长度~3 800 m,破碎带宽~100 m,走向85°~95°,倾向北东或北西,倾角55°~75°。
2 计算方法和计算模型 2.1 计算方法岩浆热液成矿是岩层形变、成矿流体流动、热传递和成矿物质等相互作用的多耦合过程[30]。目前,对于岩浆热液成矿的数值计算方法主要有有限差分法和有限单元法。其中,有限单元法是解决多物理场耦合的有效方法之一,也是解决搭建复杂模型的常用方法之一。据此,本文采用有限单元方法进行数值分析,给出研究区域金矿矿床形成的温度、流体压力等地质环境动态演化过程。
数值分析瞬态孔隙流体流动质量守恒方程(假设热液流体在流动过程中没有质量损耗)
| $ \frac{\partial }{{\partial t}}(\phi \rho ) + \nabla \cdot (\rho {\bf{u}}) = 0, $ | (1) |
式中:ϕ是孔隙度,ρ是密度,u是孔隙流体达西速度即岩浆热液多组分流动的平均速度,t是时间。
孔隙流体流动遵从达西定律
| $ \mathit{\boldsymbol{u}} = - \frac{\kappa }{\eta }(\nabla P - \rho g), $ | (2) |
式中:P是孔隙压力,κ是渗透率,η是水的黏滞系数。
根据式(1)、式(2)可推出孔隙流体运动方程[31]
| $ s\frac{{\partial P}}{{\partial t}} = \frac{\kappa }{\eta }{\nabla ^2}P, $ | (3) |
式中:s是储水率,s=ϕ Cf+(1-ϕ)Cs,Cf为流体可压缩率,Cs是固体可压缩率。
对于瞬态问题流体的热传递需要考虑固相和液相各自的热传递及固液相之间的热交换。但是,如果流体和固体之间局部传热的响应时间比相位平均温度变化的特征时间小几个数量级,那么流体和固相温度可以假定为相同,即每个点局部热平衡(local thermal equilibrium, 缩写为LTE)成立。在LTE的假设下,仅需要单个能量方程描述多孔介质内的热传递过程[13],可以写成
| $ {\rho _{\rm{r}}}c\frac{{\partial T}}{{\partial t}} + {\rho _{\rm{w}}}{c_{\rm{w}}}\mathit{\boldsymbol{u}} \cdot \nabla T = K{\nabla ^2}T + Q, $ | (4) |
式中:ρr是含孔隙流体的岩体密度,c是岩体比热,ρw是水的密度,cw是水的比热,K为岩体热导率,Q是热源(此处暂不考虑放射性热源和物质相变的能量变化)。
在计算过程中,可通过方程(3)得到每一时步的流体压力和达西速度,且将每一时步的达西速度耦合于热传递方程(4),进而可以获得岩浆热液的温度、水压力和达西速度的时空分布特征。
对于稳态问题孔隙流体运动方程为
| $ \frac{\kappa }{\eta }{\nabla ^2}P = 0, $ | (5) |
热传递方程为
| $ {\rho _{\rm{w}}}{c_{\rm{w}}}\mathit{\boldsymbol{u}} \cdot \nabla T = K{\nabla ^2}T + Q. $ | (6) |
结合已有的前河金矿矿区地质资料[24-30],我们搭建了该区二维有限元地质计算模型。沿着研究区域A-B剖面,模型长41 km,深7 km。模型中F4断裂倾角~60°,断裂宽~0.1 km。断裂带主要岩性为断裂岩、角砾岩。围岩为熊耳山群安山岩和熊耳山群英安岩。李莉等[32]对前河金矿流体包裹体研究发现该金矿成矿压力为40~60 MPa,推测该区的成矿深度约1.6~3.3 km。然而,前河金矿矿床在地表有出露,这表明随着风化剥蚀等构造运动该区至少有约1.6 km厚的地层被风化剥蚀掉了。据此,在模型建立时,我们考虑了这部分风化剥蚀的地层。
2.2.1 计算模型物质参数据熊耳山地区的地质调查和前人的研究[33-37],给出计算模型岩体、断裂和流体的物性参数,见表 1。该研究主要模拟成矿流体在流动过程中温度的变化,暂不考虑化学组分的产生与消失。杨立强等[38]对前河地区流体包裹体研究表明成矿流体以盐水为主,盐度为0.71%~17.5%,主体为1.2%~6.3%。故在本次计算中成矿岩浆热液流体设为盐水,采用盐水的物性参数作为成矿热液参数。Liu等[33]在热液成矿研究中分析盐水在不同压力和温度的密度和黏度经验公式(见式(7)、式(8)),且温度的变化对盐水密度和黏度的影响远大于压力,据此,在本研究中侧重考虑了温度变化对孔隙流体密度和黏度的影响。由式(7)、式(8)计算得出盐水盐度为5%、压力为100 MPa下盐水不同温度的密度和黏度,且在计算中据温度的不同分段赋值(表 2)。
|
|
表 1 熊耳山前河地区热液成矿数值计算参数表 Table 1 Parameters used in our calculations |
|
|
表 2 盐水密度和黏度在不同温度状况的值 Table 2 Density and viscosity at different temperature stages |
盐水密度经验公式[34]
| $ {\rho _{\rm{B}}} = {\rho _{\rm{w}}} + {\rho _{\rm{s}}}, $ | (7) |
式中:ρB为盐水密度、ρw为纯水密度,ρs为溶解质密度,它们都是关于温压的多项式,具体见Batzle等[34]的相关研究。
盐水黏度经验公式[35]
| $ \ln {\eta _w} = \sum\limits_{i = 1}^5 {{d_i}} {T^{i - 3}} + \sum\limits_{i = 6}^{10} {{\rho _w}} {d_i}{T^{i - 8}}, $ | (8) |
式中:di为常数,具体见Mao等[35]。
2.2.2 计算模型边界条件在边界条件设定时,对流体流动边界条件和流体传热边界条件分别进行设定,见图 2(a)。
|
Download:
|
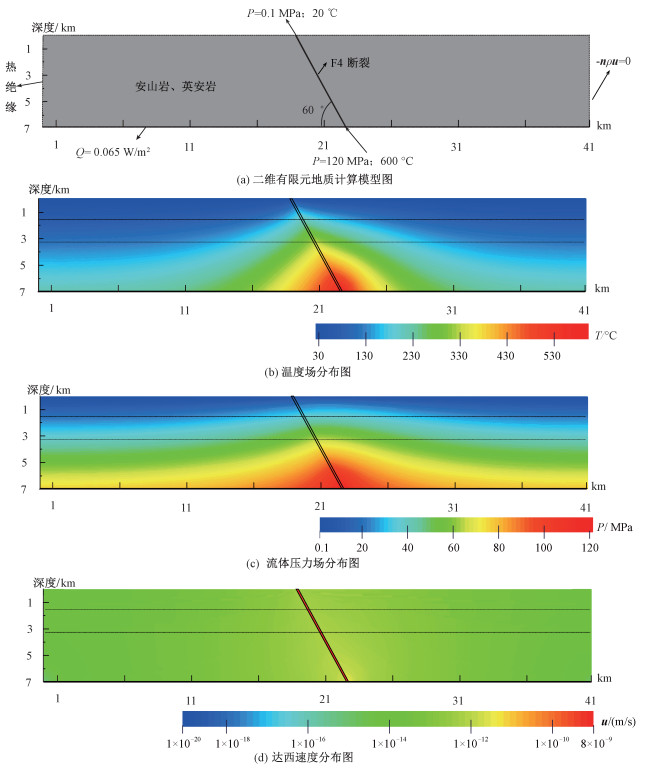
| 图 2 熊耳山前河地区热液成矿二维有限元计算模型与稳态模拟结果图 Fig. 2 Sketchmap of the two-dimensional computational model and simulation results based on 2D steady-state computations for the Qianhe region | |
对于流体流动边界条件,据赵鹏飞等[39]对热成矿底部边界条件的研究,设为2倍静水压力。考虑到孔隙流体(盐水)密度随压力温度变化,在底边界局部即断裂带底部边界给定120 MPa的压力。顶部边界为0.1 MPa(1个大气压),其余边界为法向达西速度为0,初始压力为静水压力(流体密度为1 000 kg/m3),见图 2(a)。
对于流体传热边界条件,上边界为常温边界条件(20 ℃),见图 2(a)。底边界条件,在此参照刘向冲[40]和蒋春明[41]对热液成矿数值分析研究,在断裂带底部边界设定温度为600 ℃,侧边界为热绝缘边界条件,其余底边界为热源边界(Q为大地热流,65 mW/m2[42])。另外,据何争光等[42]对华北克拉通南部现今地温场的研究可知前河地区地温梯度约为26 ℃/km。据此,整个模型初始温度设为(20+0.026y) ℃。
3 数值计算结果 3.1 稳态模拟的结果图 2给出前河地区岩浆热液系统的温度、热液流体压力和达西速度稳态模拟结果。由图 2(b)可以看出,该研究区域温度场整体上呈现为穹窿状,在同一深度上由断裂带逐渐向两侧岩层由高向低过渡,且分布与断裂倾向一致。这进一步说明断裂带是控制温度分布的重要原因。另外,断裂带温度由地下深处到地表浅处逐渐降低,到达地表时已经为常温。也就是说断裂带底部的热液流体在流向地表的过程中热量会逐渐消耗,成矿热液流体在向上运移的过程中其温度也逐渐变为有利于成矿的温度。结果显示在断裂带处,距离地表深1.6~3.3 km的范围(研究区域金矿集中区)温度基本上集中在210~330 ℃。说明在断裂带内距离地表深1.6~3.3 km的范围内可以达到利于成矿的温度条件。以上结果也表明我们计算使用的模型参数与边界条件是合理的。
图 2(c)给出研究区域流体压力的分布状态,流体压力受断裂带影响也较显著。断裂带内的压力比同深度断裂带两侧远离断裂带流体压力要大,为整个热液系统的热液流体向上运移提供了有利环境。
图 2(d)是研究区域流体达西速度图。可以看出与温度场、压力场不同,达西速度在断裂带和岩层中差别显著,达西速度在断裂带内最高可达1×10-9 m/s,而在围岩中相对较低(~1×10-14 m/s)。据此,可以对流过断裂带的热液流体的量有一个估计:断层宽为100 m且厚1 m时断层流体流量~30 m3/a,岩浆系统足以提供该流量的热液。金矿的成矿物质是由成矿流体带来的,断裂带中流体的速度大,流经断裂带的岩浆热液流体带去物质就会更多。由此可见,断裂带是有利的成矿构造,是导矿与控矿构造。
在计算过程中我们发现断裂带的宽度、底边界的压力和渗透系数是控制温度、流体压力分布的主要因素。据此,本文通过改变单一变量对这3种影响因素分别进行讨论和分析。图 3给出不同条件下温度等值线图。
|
Download:
|
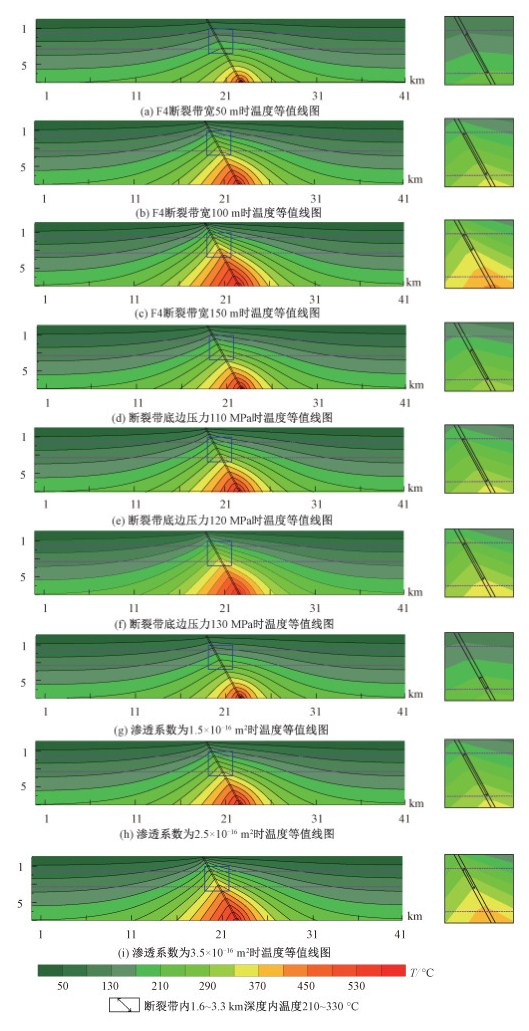
| 右侧子图为模型中蓝色线框圈中的区域放大; 箭头标出的为断裂带中在距离地表深1.6~3.3 km的范围(研究区域金矿集中区)内适合金矿形成的温度区域, 即预测的有利成矿区域。 图 3 改变单一变量下温度等值线图 Fig. 3 Change of temperature contour map with each single variable | |
首先,改变F4断裂带的宽度,分别设定为50、100和150 m 3种模型。其中,F4断裂带宽度100 m模型是对照模型。由图 3(a)~3(c)不同断裂带宽度的温度等值线分布,可以看出断裂带对温度分布的影响。当断裂带宽度100 m时,在距离地表深1.6~3.3 km的范围(研究区域金矿集中区)温度在210~330 ℃,与李莉等[32]通过对流体包裹体研究得到的成矿深度和温度均吻合。而当断裂带宽度50 m时,在相同位置温度值较断裂带宽度100 m时小。这是由于断裂带内流体总流量减小,携带传递的热量也减少,不利于温度的传递。同等温度在断裂带中出现的深度下移。在距离地表深1.6~3.3 km的范围(研究区域金矿集中区)内适合成矿的温度范围减小。断裂带在1.6~3.3 km深度范围的顶部部分区域温度低于210 ℃,该部分区域的温度不符合成矿温度。当断裂带宽度为150 m时,同等温度的分布较断裂带宽度100 m时整体上移。计算的适于成矿的温度在深度上与参考的成矿深度不完全吻合。通过这3组模型对照,可以发现断裂带的宽度会影响区域温度场的分布,进而会影响矿床的形成。值得注意的是,虽然对断裂带宽度改变幅度较大,但其对温度分布的影响并不十分显著。说明断裂带的宽度是影响矿床形成的一个因素,但该因素影响并不大。
其次,探讨F4断裂带底边界的流体压力对计算结果的影响,分别设定为110、120和130 MPa 3种模型。其中,断裂带部分底边界的压力为120 MPa是基本模型。由图 3(d)~3(f)不同断裂带底边界压力条件下的温度等值线分布图可以看出,不同底边界压力对温度的影响很大。相较于120 MPa底边界压力下计算的有利成矿温度分布与本矿区的成矿深度相吻合,压力增大或减小10 MPa都将使得有利成矿温度分布的深度区间与本矿区成矿深度不符。也就是说,在其他成矿条件不变的情况下,底边界压力过大过小都会使得有利于成矿的温度分布的深度与本矿区成矿深度存在差别。由此可见,压力是控制有利成矿温度的重要影响因素。成矿热液环境对断裂带底部压力改变有敏感的反应,这说明在成矿过程中影响导矿断裂带的岩浆系统应在一定时间内保持相对稳定状态。
最后,改变F4断裂带的渗透系数。断裂带渗透系数分别设定为1.5×10-16、2.5×10-16和3.5×10-16 m2。其中,断裂带渗透系数为2.5×10-16 m2模型是基本模型。图 3(g)~3(i)给出不同断裂带渗透系数情况下的温度等值线分布图。当渗透系数为2.5×10-16 m2时,温度分布深度区间符合本矿区的成矿深度。当渗透系数为1.5×10-16 m2时,有利成矿的温度分布的深度区间与本矿区成矿深度不符,深于本矿区成矿深度。当渗透系数为3.5×10-16 m2时温度分布的深度区间与本矿区成矿深度不完全相符,浅于本矿区成矿深度。这表明渗透系数的变大使得温度传递更为有利,渗透系数的变小不利于温度传递。
综上,对上述3个主要因素模拟情况及成矿结果做了一个总结,见表 3。
|
|
表 3 改变单一控矿因素结果汇总表 Table 3 Change of the results with each single ore-controlling factor |
稳态数值模拟计算结果得出有利成矿的温度、压力分布的深度区间与实际成矿深度基本一致,说明我们建立的前河地区二维有限元地质计算模型及参数的选取是合理的。但是,金矿的成矿过程是一个动态的过程。因此,还需给出该研究区域成矿系统温度和压力随时间变化的分布。据此,基于稳态模拟时用到的模型、物性参数与边界条件等进行瞬态数值模拟。
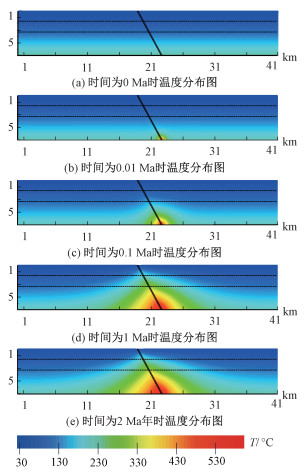
图 4为研究区域温度场随时间的变化图。可以看出,随着时间的变化温度沿断裂带向上扩散。在初始时刻,区域的温度分布为地温分布,即地温梯度为26 ℃/km。随着时间的增加,断层内热的流体向地表运动平流传输热量(advective heat transfer),温度首先在断裂带中升高,然后由断裂带向断裂带周围传递。当时间到达1 Ma时,在断裂带深1.6~3.3 km(研究区域金矿集中区)的区域内达到有利成矿的温度范围(210~330 ℃)。另外,计算结果显示在0.5 Ma时,虽然岩浆热液系统温度场还在改变,在断裂带深1.6~3.3 km(研究区域金矿集中区)的区域温度基本逐渐到达210 ℃,是利于金矿形成的温度条件。
|
Download:
|
| 图 4 瞬态温度场在不同时间模拟计算结果 Fig. 4 Change of simulated transient temperature results with time | |
图 5给出前河地区瞬态流体压力场结果,可以看出同等深度下压力由断裂向其两侧降低,且沿断裂带的传递更为明显。这是由于断裂带中的岩浆热液直接驱动下造成流体压力扩散,而围岩有较大的热惯量,被加热起来温度升高需要更多的时间。另外,由计算结果可以看出成矿过程中流体压力在断裂带内的变化比温度的变化快。但是,在2 Ma年时流体压力分布也基本与1 Ma时压力的分布相一致。流体在压力的驱动下不断流动,可成矿物质的运输提供动力条件。朱日祥等[23]的研究表明早白垩世古西太平洋板块的俯冲与滞留是华北克拉通破坏与形成有利成矿条件的原因。早白垩世古西太平洋板块在东亚大陆之下的长度大约2 000 km,按其推测的~88 km/Ma的平均后撤速率来计算,在前河地区稳定的岩浆活动是可以持续几个Ma的。说明上1 Ma的成矿时间具有可能性。

|
Download:
|
| 图 5 瞬态水压场在不同时间模拟计算结果 Fig. 5 Change of simulated water pressure results with time | |
通过上述瞬态数值模拟计算,我们发现成矿过程达到稳态要近百万年的时间,这对成矿环境要求较高。据现有的研究[43]发现高水压会使岩石的渗透性有显著改变,使得断裂带的渗透系数升高1~2个量级。据此,对渗透系数增大1个量级,由2.5×10-16 m2改为2.5×10-15 m2再次进行计算。
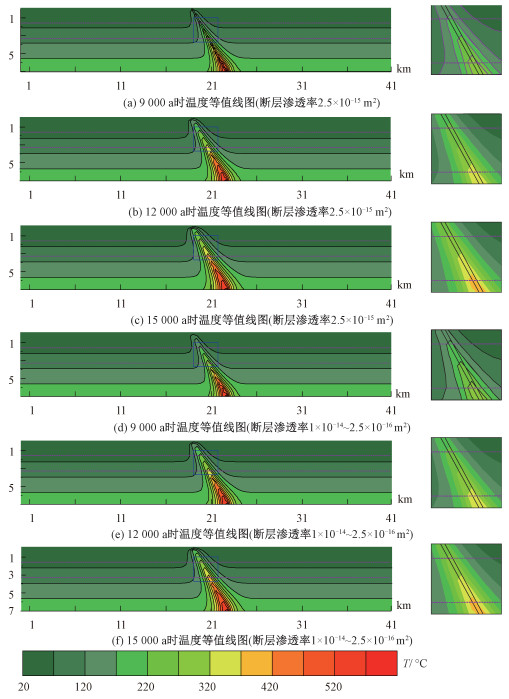
图 6(a)~6(c)给出当给定断层系统系数为2.5×10-15 m2时温度场演化过程。可以看出,断裂带的渗透系数是影响热液系统温度分布的重要因素,在高渗透率下温度的演化更为快速。在12 000~15 000 a时间段内,断裂带深1.6~3.3 km范围内基本全部到达一个适合成矿的温度条件且可持续3 000 a。此时,断裂带达西速度~2×10-7 m/s,岩层~1×10-14 m/s。到15 000 a后,有利成矿温度在成矿深度的分布逐渐减小。并且,温度沿断裂带分布的特征更加鲜明,更凸显了断裂带的控矿作用。
|
Download:
|
| (a)~(c)断层渗透率在2.5×10-15 m2时区域瞬态温度随时间变化图; (d)~(f)断层渗透率在1×10-14~2.5×10-16 m2之间以50 a为间隔相继变化时区域瞬态温度随时间变化图。 图 6 高渗透率下温度随时间的变化图 Fig. 6 Change of temperature contours with time at high permeability | |
王偲瑞等[44]及Sheldon和Micklethwaite[45]通过研究发现断裂带发生破坏,会有利于形成高渗透率,但这种高渗透率持续时间较短。Ingebritsen和Manning[46]认为断裂带高渗透率持续时间很短,往往只能持续数年到千年的时间。进一步加大渗透系数进行模拟发现,当渗透率为1×10-14 m2时,1 000 a左右可达到利于成矿的温度条件。那么,断裂带能否维持这么长时间的高渗透率尚不清楚。据此,需考虑到断层的活动性,我们补充了多渗透系数变化模型,分别将断层渗透率设为在1×10-14~2.5×10-16 m2之间以50 a间隔相继变化。图 6(d)~6(f)计算结果显示,在9 000 a左右断裂带在1.6~3.3 km的深度上温度是有利于成矿的。这说明高渗透率在断裂带内断续的出现也可以达到利于成矿的温度环境。热液系统对断裂带的渗透系数改变敏感性可能表示金矿形成时岩浆系统所处的不同状态。当渗透率为2.5×10-16 m2时,热液系统在断裂带深1.6~3.3 km(研究区域金矿集中区)范围内达到合适的成矿温度需要近百万年的时间。当渗透率为2.5×10-15 m2时,适合成矿的温度到达稳定状态需要几千年。间断出现高渗透率达到成矿温度也需要几千年时间。在熊耳山地区金矿的成矿期,该地区岩浆活动和构造活动频繁,这使得断裂带内有机会出现间断的高渗透性。这种间断的高渗透性有可能使断裂带深1.6~3.3 km范围内适合成矿的温度保持数千年。即使在岩浆系统活动较剧烈、构造频繁的环境中依然可以具备金矿形成的温度条件,并且,剧烈、频繁断裂带破坏活动正是造成断裂带孔隙结构破坏进一步增大渗透系数的原因。
4 结论前河金矿是熊耳山地区具有代表性的热液型金矿,成矿时间是早白垩纪,且形成过程可能与华北克拉通的破坏有关。在早中生代燕山期,该区发生了大规模岩浆活动,这为该地区的岩浆热液系统形成提供了热液流体的来源。根据前人对岩浆热液成矿研究的基础上,结合现今前河地区地质背景,搭建二维有限元地质模型。通过稳态数值模拟计算,获得前河金矿形成的基本计算模型、物性参数与边界条件等参数,模拟的温压分布与前人通过研究流体包裹体推断的成矿压力、温度与深度相吻合(即成矿深度1.6~3.3 km,断裂带温度达到210~330 ℃范围)。据此,进行瞬态数值计算,初步得出:1)在成矿过程中高温流体主要沿断裂带传送,造成断裂带中温度升高,并传递给周围围岩。参数不同,特别是断层渗透率可以有数量级的变化,对沿断裂带多长时间可以达到岩浆热液成矿系需要的温度条件有显著影响。低渗透率时可能要百万年时间才能逼近稳态;而高渗透率时数千年就能达成适合成矿的温度条件,并且这种温度条件可以持续数千年。高渗透系数与低渗透系数可能解释不同岩浆环境时金矿形成的原因。2)热液成矿的主要影响因素是热液在断层带中流过携带的物质和热量。平流传递的总热量与断层宽度、热液源头的流体温度压力、断层渗透率的大小等有关。断层渗透率越高、源头压力越大、温度越高,断层内的热液流速就越大、平流传递的热流密度就越大;而同样热流密度下,如果断层越宽,则传输的总热量越大,更有利于在较短的时间段内,达到在特定压力下利于金矿生成的温度,形成金矿。在这些影响因素中,由于只有断层带的渗透率可以变化几个数量级,它的影响就更为显著,在研究中值得特别注意。
综上所述,断裂带对成矿的温度、流体压力演化有明显的控制作用。断裂带的渗透率高于围岩,在断裂带中成矿流体的达西速度较岩层中高几个量级。表明断裂带为成矿物质的运移和富集提供了场所。从数值模拟的角度验证断裂带是主要的导矿控矿构造,韧-脆性和脆性断裂带往往有较高的渗透率是找矿的有利区域。
感谢中国科学院大学王世民教授提供的COMSOL软件程序包及使用上的指导。| [1] |
张元厚, 张世红. 岩浆热液系统金矿床研究进展[J]. 黄金, 2005, 26(10): 14-18. |
| [2] |
曾庆丰. 热液成矿多元论[J]. 地质科学, 1985(2): 145-153. |
| [3] |
宋焕斌, 戴福盛. 论热液矿床的分类[J]. 矿床地质, 1992, 11(3): 286-290. |
| [4] |
Hedenquist J W, Lowenstern J B. The role of magmas in the formation of hydrothermal ore deposits[J]. Nature, 1994, 370(6490): 519-527. Doi:10.1038/370519a0 |
| [5] |
曾庆丰. 矿液运移问题[J]. 科学通报, 1981, 26(3): 166-168. |
| [6] |
Hustonl D L. The hydrothermal environment[J]. Journal of Australian Geophysics & Geophysics, 1998, 17(4): 15-30. |
| [7] |
邵洁涟, 梅建明. 浙江火山岩区金矿床的矿物包裹体标型特征研究及其成因与找矿意义[J]. 矿物岩石, 1986, 6(3): 103-111. |
| [8] |
武广, 孙丰月, 赵财胜, 等. 额尔古纳成矿带西北部金矿床流体包裹体研究[J]. 岩石学报, 2007, 23(9): 2227-2240. Doi:10.3969/j.issn.1000-0569.2007.09.021 |
| [9] |
张德会, 徐九华, 余心起, 等. 成岩成矿深度:主要影响因素与压力估算方法[J]. 地质通报, 2011, 30(1): 112-125. Doi:10.3969/j.issn.1671-2552.2011.01.012 |
| [10] |
陈柏林. 从成矿构造动力学探讨脉状金矿床成矿深度[J]. 地质科学, 2001, 36(3): 380-384. Doi:10.3321/j.issn:0563-5020.2001.03.014 |
| [11] |
吕古贤, 林文蔚, 郭涛, 等. 金矿成矿过程中构造应力场转变与热液浓缩-稀释作用[J]. 地学前缘, 2001, 8(4): 253-264. Doi:10.3321/j.issn:1005-2321.2001.04.003 |
| [12] |
安芳, 朱永峰. 热液金矿成矿作用地球化学研究综述[J]. 矿床地质, 2011, 30(5): 799-841. Doi:10.3969/j.issn.0258-7106.2011.05.004 |
| [13] |
Gamal A, Piotr F. Problems of modeling flow and heat transfer in porous media[J]. 1997, 85: 55-88.
|
| [14] |
Zhang Y, Hobbs B E, Ord A, et al. The influence of faulting on host-rock permeability, fluid flow and ore genesis of gold deposits:a theoretical 2D numerical model[J]. Journal of Geochemical Exploration, 2003, 78(s 78/79): 279-284. |
| [15] |
Zhao C B, Hobbs B E, Mühlhaus H B. Finite element analysis of heat transfer and mineralization in layered hydrothermal systems with upward through flow[J]. Computer Methods in Applied Mechanics and Engineering, 2000, 186(1): 49-64. Doi:10.1016/S0045-7825(99)00104-8 |
| [16] |
张嵩松.岩浆热液成矿系统的数值模拟[D].武汉: 中国地质大学, 2011.
|
| [17] |
李正君.内蒙古毕力赫金矿成矿流体数值模拟[D].北京: 中国地质大学, 2013.
|
| [18] |
Liu X C, Xing H, Zhang D H. Fluid focusing and its link to vertical morphological zontion at the Dajishan vein-type tungsten deposit, South China[J]. Ore Geology Reviews, 2014, 62(1): 245-258. Doi:10.1016/j.oregeorev.2014.04.005 |
| [19] |
Liu X C, Xing H, Zhang D H. The mechanisms of the textures and its implications for the five-floor zonation at the Dajishan vein-type tungsten deposit, China[J]. Ore Geology Reviews, 2015, 65: 365-374. Doi:10.1016/j.oregeorev.2014.10.011 |
| [20] |
Xing H. Finite element simulation of transient geothermal flow in extremely heterogeneous fractured porous media[J]. Journal of Geochemical Exploration, 2014, 144: 168-178. Doi:10.1016/j.gexplo.2014.03.002 |
| [21] |
Ingebritsen S E, Appold M S. The physical hydrogeology of ore deposits[J]. Economic Geology, 2012, 107: 559-584. Doi:10.2113/econgeo.107.4.559 |
| [22] |
唐克非.华北克拉通南缘熊耳山地区金矿床时空演化、矿床成因及成矿构造背景[D].武汉: 中国地质大学, 2014.
|
| [23] |
朱日祥, 范宏瑞, 李建威, 等. 克拉通破坏型金矿床[J]. 中国科学:地球科学, 2015, 45(8): 1153-1168. |
| [24] |
王浩. 熊耳山金矿集区成矿模式及典型矿床研究[J]. 中国金属通报, 2016(11): 74-76. |
| [25] |
徐浩, 王庆飞, 杨立强, 等. 成矿多过程耦合模型数值模拟研究态势[J]. 矿产与地质, 2006, 20(Z1): 494-497. |
| [26] |
吴发富.熊耳山矿集区燕山期金成矿系统[D].北京: 中国地质大学(北京), 2010.
|
| [27] |
刘永春. 河南省前河金矿控矿构造及其与成矿的关系[J]. 贵金属地质, 1993, 2(3): 188-197. |
| [28] |
朱沛云, 胡斌, 赖峰, 等. 河南省前河金矿矿床成因及成矿模式探讨[J]. 地质找矿论丛, 2014, 29(2): 199-205. |
| [29] |
毛付龙.河南前河金矿构造控矿规律分析及成矿预测[D].北京: 中国地质大学(北京), 2008.
|
| [30] |
张元厚, 张世红, 韩以贵, 等. 华熊地块马超营断裂走滑特征及演化[J]. 吉林大学学报(地球科学版), 2006, 36(2): 1671-5888. |
| [31] |
Mohammad M, Pramod K P. Diffusion equation for fluid flow in porous rocks[J]. Journal of Science (JOS) ISSN, 2015, 4(S2): 418-425. |
| [32] |
李莉, 卿敏, 陈祥. 河南前河金矿床地球化学特征[J]. 黄金地质, 1999(3): 75-80. |
| [33] |
Liu X, Xing H, Zhang D. Influences of fluid properties on the hydrothermal fluid flow and alteration halos at the Dajishan tungsten deposit, China[J]. Journal of Geochemical Exploration, 2016, 163: 53-69. Doi:10.1016/j.gexplo.2016.01.014 |
| [34] |
Batzle M L, Wang Z. Seismic properties of pore fluid[J]. Geophysics, 1992, 57(11): 1396-1408. Doi:10.1190/1.1443207 |
| [35] |
Mao S, Duan Z. The viscosity of aqueous alkali-chloride solutions up to 623K, 1000bar, and high ionic strength[J]. Thermophys, 2009, 30(5): 1510-1523. Doi:10.1007/s10765-009-0646-7 |
| [36] |
岑况, 於崇文. 铜陵地区硫化物矿床成矿过程的热传导和物质输运动力学[J]. 地球化学, 2001(6): 533-539. Doi:10.3321/j.issn:0379-1726.2001.06.005 |
| [37] |
陈颙, 黄庭芳, 刘恩儒. 岩石物理学[M]. 北京: 北京大学出版社, 2001: 1-294.
|
| [38] |
杨立强, 王中亮, 吴发富, 等. 河南前河金矿床成矿流体特征与来源:流体包裹体地球化学与同位素约束[J]. 矿物学报, 2009, 29(S1): 259-260. |
| [39] |
赵鹏飞, 王功文, 韩小梦, 等. 基于FLAC3D成矿过程数值模拟:以南泥湖钼矿床为例[J]. 中国矿业, 2017, 26(S1): 286-297. |
| [40] |
刘向冲.江西大吉山石英脉型黑钨矿床"五层楼"垂直形态分带动力学机制[D].北京: 中国地质大学(北京), 2014.
|
| [41] |
蒋春明.三维建模及数值模拟技术在矿床研究中的应用[D].长沙: 中南大学, 2012.
|
| [42] |
何争光, 刘池洋, 赵俊峰, 等. 华北克拉通南部地区现今地温场特征及其地质意义[J]. 地质论评, 2009, 55(3): 428-434. Doi:10.3321/j.issn:0371-5736.2009.03.014 |
| [43] |
倪绍虎, 何世海, 汪小刚, 等. 裂隙岩体高压渗透特性研究[J]. 岩石力学与工程学报, 2013, 32(S2): 3028-3035. |
| [44] |
王偲瑞, 杨立强, 孔鹏飞. 焦家断裂渗透性结构与金矿床群聚机理:构造应力转移模拟[J]. 岩石学报, 2016, 32(8): 2494-2508. |
| [45] |
Sheldon H A, Micklethwaite S. Damage and permeability around faults:implications for mineralization[J]. Geology, 2007, 35(10): 903-906. Doi:10.1130/G23860A.1 |
| [46] |
Ingebritsen S E, Manning C E. Permeability of the continental crust:dynamic variations inferred from seismicity and metamorphism[J]. Geofluids, 2010, 10(1/2): 193-205. |
 2020, Vol. 37
2020, Vol. 37 


