液滴撞击固体壁面现象广泛存在于动力机械、喷雾冷却、喷涂印染和薄膜材料沉积制备等工业领域。液滴的物性、撞击基面的理化特性以及撞击时的条件决定液滴撞击固体壁面后的动力学行为。
关于水、乙醇等牛顿流体液滴撞击固体壁面的行为,相关学者已经进行了大量研究[1-2]。在工业生产过程中,实际使用的流体常因添加了纳米颗粒、高分子材料或分散剂而表现出如剪切变稀、剪切增稠、屈服应力等非牛顿流体特性。目前关于非牛顿液体液滴撞击固体壁面行为的研究尚少,Bergeron等[3]发现在牛顿流体中添加微量的高分子材料可以明显抑制液滴在基面上的回弹行为。Huh等[4]指出随着高分子添加物质量分数与分子量的增大,流体的黏弹性逐渐增大,液滴撞击固体壁面后的回缩趋势减小。German和Bertola[5]研究指出对于表现出剪切变稀特性的幂律流体液滴,对比幂律指数m,稠度系数k在液滴撞击铺展过程中起着更重要的作用。An和Lee[6-7]研究剪切变稀流体液滴撞击固体壁面的动力学行为后指出铺展过程中动态变化的剪切黏度影响液滴的撞击铺展行为。Vega和Castrejón-Pita[8]研究发现添加高分子材料PAA后牛顿流体表现出剪切变稀特性,液滴撞击壁面后的溅射行为被显著抑制。刘海龙等[9]研究纳米流体液滴撞击固体壁面的动力学行为后指出,纳米颗粒的加入在使流体表现出剪切变稀特性的同时也提高了其剪切黏度,液滴撞击固体壁面后的铺展行为被显著抑制。
采用数值模拟研究液滴撞击固体壁面行为的难点是移动相界面的求解。常用的相界面求解方法包括流体体积法(VOF, volume of fluid)、水平集方法(level set method)、格子玻尔兹曼方法(lattice Boltzmann method)和扩散界面法(diffuse interface method)等。基于VOF方法捕捉相界面的移动,Jian等[10]模拟研究环境气体物性对液滴撞击壁面后产生飞溅的影响,揭示气体惯性力、黏性力以及密度对飞溅行为的影响机制。Jeong等[11-12]基于有限元法耦合水平集方法捕捉相界面的移动,模拟研究含颗粒液滴撞击固体壁面后的液滴及液滴内颗粒的动力学行为,结果表明颗粒的存在会增加液滴铺展过程中的能量耗散,进而抑制液滴撞击固体壁面后的振动行为。Mukherjee和Abraham[13]基于格子玻尔兹曼方法建立液滴撞击固体壁面的轴对称模型,研究液滴撞击固体壁面后韦伯数、奥尼索数以及前进和后退接触角对液滴沉积和回弹临界范围的影响机制。Khatavkar等[14]利用扩散界面法研究壁面浸润性对微米级液滴撞击固体壁面行为的影响机制,结果表明随着壁面疏水性的增大,液滴平衡后与壁面的接触直径减小,接触角达到120°时,液滴撞击固体壁面后完全回弹。有关液滴撞击固体壁面的数值模拟研究,主要集中于牛顿流体液滴,通过数值模拟手段深入研究非牛顿流体液滴撞击固体壁面的行为亟待开展。
本文将石墨烯和多壁碳纳米管均匀分散到环氧树脂中,配制均匀稳定的纳米流体,利用高速摄像技术实验研究纳米流体液滴撞击固体壁面的动力学行为。同时基于有限元法,采用水平集方法捕捉相界面的移动,利用截断的幂律模型耦合纳米颗粒带来的非牛顿特性,构建纳米流体液滴撞击固体壁面的数值模型,通过数值模拟手段研究纳米颗粒对液滴撞击壁面后动力学行为的影响机制。
1 实验方法本文选用的纳米颗粒为片状的石墨烯(厚度3.4~7 nm,片层直径10~50 μm,层数5~10,纯度为95%,苏州碳丰石墨烯科技有限公司)以及经酸化处理后的圆柱状的多壁碳纳米管(直径小于8 nm,长度0.5~2 μm,羧基含量为3.86wt%,纯度为98%,中国科学院成都有机化学研究所)。基液为W52型环氧树脂(环氧值0.44~0.48,密度为1 100 kg/m3,黏度为1.57 Pa·s)。在纳米流体中纳米颗粒常因范德华力而团聚,故本研究采用超声波破碎技术将纳米颗粒均匀分散并利用基液的高黏性力克服纳米颗粒的团聚,在不引入分散剂的情况下成功配制均匀稳定的纳米流体。
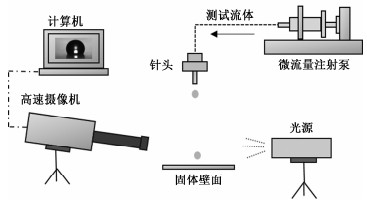
图 1为用于观察纳米流体液滴撞击固体壁面行为的可视化实验平台。通过微流量注射泵和针头(G21,内径0.5 mm)控制液滴的尺寸和产生频率。使用高速数码相机(Phantom V1611,Dantec Dynamics),配合显微镜头对液滴撞击固体壁面的过程进行显微拍摄(10 000 fps)。
|
Download:
|
| 图 1 实验装置示意图 Fig. 1 Schematic of the experimental apparatus | |
通过改变液滴与撞击底板之间的距离获得不同的撞击速度,同时根据液滴撞击基板的临界图像与其上一帧图像的垂直距离差与两张图像时间间隔的比值计算撞击速度的大小。由于所配制的纳米流体的表面张力差异不大((54±1) mN/m),实验研究中产生的液滴直径的变化范围也较小,约为(2.5±0.05) mm,在模拟研究中,将液滴直径统一设置为2.5 mm。实验采用韦伯数We=ρ2V2D0/σ对液滴撞击条件进行描述,其中ρ2为液滴密度,V为撞击速度,σ为表面张力系数,D0为液滴初始直径。本文基于图像分析软件ImageJ获得液滴铺展过程的接触角及无量纲参数变化,实验及测量的累积误差为5%。本研究中环氧树脂和纳米流体的密度为1 100 kg/m3,实验温度及纳米流体物性测试温度均为25 ℃,液滴撞击实验选择的基面为亲水性的玻璃板。纯环氧树脂液滴在玻璃板上的静态接触角为(23+1)°。
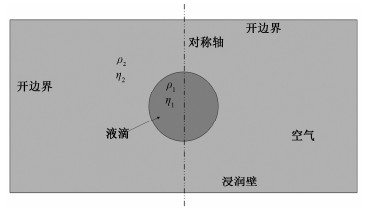
2 数值计算模型基于有限元法,本研究建立计算域设置如图 2所示的数值模型,模拟二维轴对称的液滴撞击固体壁面的行为。液滴以初始速度撞击壁面,下边界为浸润壁边界条件,计算过程中接触角恒定,上边界及左右边界为开边界,该边界条件将边界处法向应力设置为零,描述边界与无限大气体区域接触的情况。
|
Download:
|
| 图 2 液滴撞击壁面计算域设置 Fig. 2 Computation domain for droplet impacting on surface | |
数值模拟中采用不可压缩流体的Navier-Stokes方程描述流体的质量和动量传递特性。为了耦合表面张力的影响,在方程中添加表面张力项。因此,本文数值模拟研究中所求解的Navier-Stokes方程为
| $\nabla \cdot \boldsymbol{u}=0, $ | (1) |
| $\rho\left(\frac{\partial \boldsymbol{u}}{\partial \mathrm{t}}+\boldsymbol{u} \cdot \nabla\right) \boldsymbol{u}=\nabla \cdot\left[-P \boldsymbol{I}+\boldsymbol{\eta}\left(\nabla \boldsymbol{u}+(\nabla \boldsymbol{u})^{\mathrm{T}}\right)\right]+\rho g+\boldsymbol{F}_{\mathrm{st}}. $ | (2) |
式中:ρ为密度, u为速度, η为动力黏度, t为时间, P为压力, g为重力加速度, Fst为作用于气体与液体间的表面张力,I为单位矩阵。
在本文的数值模拟研究工作中,表面张力采用下式计算Fst=▽·((σ(I-nnT))δ)。式中:n为界面法向量; σ为表面张力系数;δ为狄拉克函数,该函数仅在流体界面为非零值。
将与流体界面接触的固体壁的边界条件设置为浸润壁。此边界条件将垂直于壁的速度分量设为零,即
| $\boldsymbol{u} \cdot \boldsymbol{n}_{\text {wall }}=0. $ | (3) |
作用在壁面上的合力为
| $\boldsymbol{F}_{\text {wall }}=\sigma\left(\boldsymbol{n}_{\text {wall }}-(\boldsymbol{n} \cos \theta)\right) \delta-\frac{\eta}{\beta} \boldsymbol{u}, $ | (4) |
式中:β为滑移长度[15],nwall为浸润壁面处的法向量,通过浸润壁边界条件指定接触角θ。本文中,将接触角设置为60°,滑移长度设置为网格单元尺寸h。
本文采用幂律模型耦合非牛顿特性对液滴撞击壁面后动态行为的影响。在幂律模型中,黏度根据以下公式得出
| $\eta(\dot{\gamma})=k \dot{\gamma}^{m-1}, $ | (5) |
式中:k是稠度指数,m是幂律指数,$\dot{\gamma}$为剪切速率。同时为避免幂律模型在剪切速率过低时黏度失真的情况,将幂律模型通过下式[16]进行截断修正:
| $\dot{\gamma}=\max \left(\sqrt{\boldsymbol{S}}: \sqrt{\boldsymbol{S}}, \dot{\gamma}_{\min }\right), \left\{\boldsymbol{S}=\frac{1}{2}\left[\nabla \boldsymbol{u}+(\nabla \boldsymbol{u})^{\mathrm{T}}\right], \right\}\\ \left\{\dot{\gamma}_{\min }=0.01 \mathrm{s}^{-1}\right\} $ | (6) |
采用水平集方法追踪相界面的移动时,在气体中水平集函数ϕ=0, 在液体中ϕ=1。因此,水平集函数可视为流体的体积分数,两相流体界面间的物质传递由下式水平集方程给定
| $\frac{\partial \phi}{\partial t}+\boldsymbol{u} \cdot \nabla \phi=\gamma \nabla \cdot\left(\varepsilon \nabla \phi-\phi(1-\phi) \frac{\nabla \phi}{|\nabla \phi|}\right), $ | (7) |
式中:ε参数决定界面的厚度,通常将界面厚度设置为界面经过的区域中的特征网格尺寸的一半;γ参数决定界面重新初始化的数量,比较合适的γ值是模型中出现的最大速度大小。通过Heaviside函数对界面处的密度和黏度进行光滑处理[17]:
| $\phi=\left\{\begin{array}{ll}0, & \phi \leqslant-\varepsilon \\ \frac{1}{2}+\frac{\phi}{2 \varepsilon}+\frac{1}{2 \pi} \sin \frac{\pi \phi}{\varepsilon} & , -\varepsilon<\phi<\varepsilon \\ 1, & \phi \geqslant \varepsilon\end{array}\right. $ | (8) |
光滑处理后,流体的密度和黏度可表示为:
| $\rho=\rho_{1}+\left(\rho_{2}-\rho_{1}\right) \phi\\ \eta=\eta_{1}+\left(\eta_{2}-\eta_{1}\right) \phi $ | (9) |
相界面的位置可由ϕ(x, t)=0.5时的等值线表示。
表 1为模拟纯环氧树脂液滴撞击壁面过程相关参数的设置
|
|
表 1 数值模拟参数设置 Table 1 Parameters in numerical simulation |
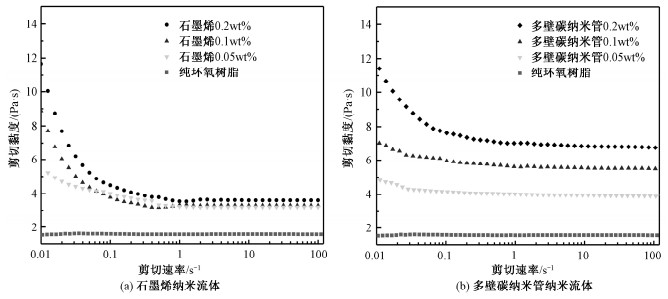
图 3为采用旋转式流变仪(Discovery DHR-Ⅱ,TA)测得的环氧树脂和纳米流体的剪切黏度曲线。从图中可以看出,纯的环氧树脂的剪切黏度不随剪切速率的变化而改变,表现出牛顿流体的特性。而添加了纳米颗粒的环氧树脂不仅表现出不同剪切变稀程度的非牛顿流体特性,同时其整个剪切速率区间内的剪切黏度都显著增大。
|
Download:
|
| 图 3 纳米流体剪切黏度曲线 Fig. 3 Shear viscosity of the prepared nanofluids | |
图 4为高速摄像系统捕捉的液滴撞击固体壁面的动态过程。可以看到,相比纳米流体液滴,纯环氧树脂液滴在撞击固体壁面的的变化幅度更大,在达到最大铺展并开始回缩之前,液滴的形状更为扁平。而相比添加了石墨烯纳米颗粒的纳米流体液滴,碳纳米管纳米流体液滴的变化幅度更小,这是由于碳纳米管纳米流体的剪切黏度更高,撞击过程中的黏性耗散更大,只有较少的惯性能量转化为表面能量。

|
Download:
|
| 图 4 液滴撞击固体壁面的动态过程(V=3.43 m/s) Fig. 4 Image sequences of the impacting process of droplet on solid surfaces | |
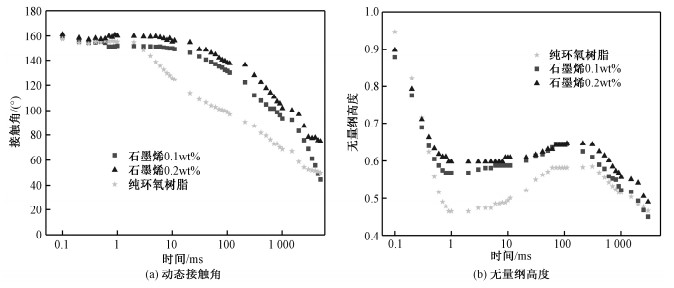
为了定量地分析纳米颗粒的加入对液滴撞击固体壁面行为的影响,本文定义无量纲参数:无量纲高度H*=Ht/H0,式中H0代表液滴撞击固体壁面的初始高度,Ht代表液滴撞击固体壁面过程中动态变化的高度;无量纲直径D*=Dt/D0,其中D0代表液滴撞击壁面的初始直径,Dt是液滴撞击固体壁面过程中动态变化的直径。从图 5(a)中可以发现,对比纯的环氧树脂液滴与添加了石墨烯颗粒的环氧树脂液滴,动态接触角在铺展阶段仅表现出轻微的不同,而在回缩阶段表现出显著的差异。添加了石墨烯纳米颗粒的纳米流体液滴在回缩阶段的接触角显著大于纯环氧树脂液滴,随着纳米颗粒质量分数的增大,回缩阶段的接触角也在增大。图 5(b)为液滴撞击固体壁面后的无量纲高度的变化曲线,可以看出在0.5 ms之前,不同液滴的无量纲高度差异不大,原因是这一阶段主导液滴动态变化的主要是液滴的惯性力。在0.5 ms后,纯环氧树脂液滴的无量纲高度继续下降,而石墨烯纳米流体液滴的无量纲高度在此后的减小幅度较小,质量分数较大的石墨烯纳米流体液滴的无量纲高度略大。纳米颗粒的加入使得环氧树脂基液的黏度增大,液滴铺展过程中的黏性耗散增加,同时纳米颗粒的存在使液滴与壁面间的摩擦耗散增加。液滴的惯性能量中被转化为表面能的比例较少,液滴撞击壁面过程的动力学行为受到了显著抑制。
|
Download:
|
| 图 5 液滴撞击固体壁面过程中动态接触角和无量纲高度随时间变化曲线(V=3.43 m/s) Fig. 5 Variations in dynamic contact angle and dimensionless height of droplet impacting on surface (V=3.43 m/s) | |
流变学分析表明纳米流体表现出不同程度的剪切变稀特性。在数值模拟研究中,我们通过截断的幂律模型耦合纳米颗粒带来的剪切变稀特性。首先模拟纯环氧树脂液滴(k=1.57, m=1)撞击壁面的情况,随后在固定稠度系数k的情况下,改变幂律指数m,研究剪切变稀特性对纯环氧树脂液滴撞击铺展行为的影响。从图 6可以看出,随着幂律指数m的减小,液滴撞击壁面后的高度更低,铺展直径更大。

|
Download:
|
| 图 6 不同幂律指数液滴撞击壁面动态过程(V=1.71 m/s) Fig. 6 Simulation snapshots of droplet impacting on surface at different power-law indexes (V=1.71 m/s) | |
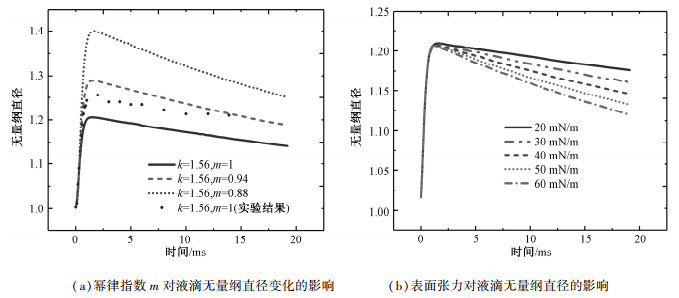
图 7(a)为不同幂律指数液滴撞击壁面过程中无量纲直径随时间的变化规律。实线上方的数据散点为实验研究中纯环氧树脂液滴撞击壁面过程中无量纲直径,实线为数值模拟结果中无量纲直径的变化曲线。可以看出实验结果与数值模拟结果的变化趋势一致且误差较小(≤4%), 数值模拟结果和实验结果出现差异的原因是,在液滴的初始铺展阶段,液滴的实际接触角大于数值模拟的设置值,故此阶段数值模拟结果中液滴的铺展直径略大于实验结果,这表明我们的数值模型能够较准确地模拟液滴撞击固体壁面的行为。由图 7(a)可以定性地发现随着幂律指数的减小,液滴最大无量纲直径增大。其原因是随着幂律指数的减小,在剪切速率较高时,液滴的黏度减小得更多。黏性耗散的减小使得液滴的惯性能量更多地被转化为表面能量(铺展得更大),虽然随着铺展直径的增大,液滴与壁面间的摩擦耗散增大,但黏性耗散显然在此过程中起着更为重要的主导作用。
|
Download:
|
| 图 7 液滴无量纲直径变化曲线(V=1.71 m/s) Fig. 7 Variation in the dimensionless diameter of droplet (V=1.71 m/s) | |
虽然本文配制的纳米流体的表面张力与基液变化不大,但众多工业应用中的纳米流体常因添加了活性剂而造成表面张力的改变。因此本文基于建立的数值模型,考察表面张力大小对液滴撞击壁面后铺展行为的影响。从图 7(b)中不同表面张力的液滴撞击壁面后无量纲直径随时间的变化可以看出,在液滴的铺展阶段(达到最大铺展直径之前),表面张力对最大铺展直径及达到最大铺展直径所需要的时间影响不大。但在液滴的回缩阶段(达到最大铺展之后),随着表面张力的增大,液滴回缩后的无量纲直径显著减小。
4 结论本文配制表现出非牛顿剪切变稀特性的纳米流体,通过高速摄像技术实验研究纳米流体液滴撞击固体壁面的动力学行为。基于有限元方法,耦合水平集方法捕捉相界面的移动,构建非牛顿流体液滴撞击固体壁面的数值模型。研究结果表明,纳米颗粒的加入不仅使环氧树脂基液的剪切黏度增大,同时使其表现出剪切变稀的非牛顿流体特性。纳米颗粒的加入会抑制液滴在撞击壁面过程中的铺展行为,抑制程度随着纳米颗粒质量分数的增大而增大。对于相同稠度系数的液滴,随着幂律指数m的减小,液滴撞击固体壁面后的变化范围更大。表面张力主要影响着液滴铺展后的回缩阶段,此时随着表面张力的增大,液滴的无量纲直径逐渐减小。
| [1] |
Yarin A L. Drop impact dynamics:splashing, spreading, receding, bouncing…[J]. Annu Rev Fluid Mech, 2006, 38: 159-192. Doi:10.1146/annurev.fluid.38.050304.092144 |
| [2] |
Josserand C, Thoroddsen S T. Drop impact on a solid surface[J]. Annual Review of Fluid Mechanics, 2016, 48(1): 365-391. Doi:10.1146/annurev-fluid-122414-034401 |
| [3] |
Bergeron V, Bonn D, Martin J Y, et al. Controlling droplet deposition with polymer additives[J]. Nature, 2000, 405(6788): 772. Doi:10.1038/35015525 |
| [4] |
Huh H K, Jung S, Seo K W, et al. Role of polymer concentration and molecular weight on the rebounding behaviors of polymer solution droplet impacting on hydrophobic surfaces[J]. Microfluidics and Nanofluidics, 2015, 18(5/6): 1221-1232. |
| [5] |
German G, Bertola V. Impact of shear-thinning and yield-stress drops on solid substrates[J]. Journal of Physics:Condensed Matter, 2009, 21(37): 375111. Doi:10.1088/0953-8984/21/37/375111 |
| [6] |
An S M, Lee S Y. Observation of the spreading and receding behavior of a shear-thinning liquid drop impacting on dry solid surfaces[J]. Experimental Thermal and Fluid Science, 2012, 37: 37-45. Doi:10.1016/j.expthermflusci.2011.09.018 |
| [7] |
An S M, Lee S Y. Maximum spreading of a shear-thinning liquid drop impacting on dry solid surfaces[J]. Experimental Thermal and Fluid Science, 2012, 38: 140-148. Doi:10.1016/j.expthermflusci.2011.12.003 |
| [8] |
Vega E J, Castrejón-Pita A A. Suppressing prompt splash with polymer additives[J]. Experiments in Fluids, 2017, 58(5). Doi:10.1007/S00348-017-2341-y |
| [9] |
刘海龙, 沈学峰, 王睿, 等. 纳米流体液滴撞击壁面铺展动力学特性研究[J]. 力学学报, 2018, 50(5): 1024-1031. |
| [10] |
Jian Z, Josserand C, Popinet S, et al. Two mechanisms of droplet splashing on a solid substrate[J]. Journal of Fluid Mechanics, 2018, 835: 1065-1086. Doi:10.1017/jfm.2017.768 |
| [11] |
Jeong H J, Hwang W R, Kim C, et al. Numerical simulations of capillary spreading of a particle-laden droplet on a solid surface[J]. Journal of Materials Processing Technology, 2010, 210(2): 297-305. Doi:10.1016/j.jmatprotec.2009.09.014 |
| [12] |
Jeong H J, Hwang W R, Kim C. Numerical simulations of the impact and spreading of a particulate drop on a solid substrate[J]. Modelling and Simulation in Engineering, 2012, 1-10. |
| [13] |
Mukherjee S, Abraham J. Investigations of drop impact on dry walls with a lattice-Boltzmann model[J]. Journal of Colloid and Interface Science, 2007, 312(2): 341-354. Doi:10.1016/j.jcis.2007.03.004 |
| [14] |
Khatavkar V V, Anderson P D, Duineveld P C, et al. Diffuse-interface modelling of droplet impact[J]. Journal of Fluid Mechanics, 2007, 581: 97. Doi:10.1017/S002211200700554X |
| [15] |
Shikhmurzaev Y D. The moving contact line on a smooth solid surface[J]. International Journal of Multiphase Flow, 1993, 19(4): 589-610. Doi:10.1016/0301-9322(93)90090-H |
| [16] |
Liu H L, Moon J S, Hwang W R. Numerical simulation of a shear-thinning fluid through packed spheres[J]. Korea-Australia Rheology Journal, 2012, 24(4): 297-306. Doi:10.1007/s13367-012-0036-8 |
| [17] |
Olsson E, Kreiss G. A conservative level set method for two phase flow[J]. Journal of Computational Physics, 2005, 210(1): 225-246. Doi:10.1016/j.jcp.2005.04.007 |
 2020, Vol. 37
2020, Vol. 37 


