食品、化工、医药、废水处理等领域常需要将不相溶的液体进行混合,液液相间的充分接触与均匀的粒径分布有利于增强相间传热传质效果,提高反应效率。传统的机械搅拌、高压混合等增强乳化效果的方法能在一定程度上增强相间作用,但由于反应器内流场分布不均匀,导致液滴粒径分布均匀性较差,且存在能耗高、效率低等缺点。探索新型高效的液液相间强化传质技术逐渐成为近年来的发展趋势。新出现的微结构[1]、空化[2]、多孔膜[3]、电场[4-5]等液液相间强化技术以能耗低、效率高的优势不断受到研究者的关注。作为一种新型过程强化方法,高压电场在促进多相反应和相间传质方面具有显著优势[6]。电场作用下液体将破碎成超细液滴群,液滴粒径分布均匀性提高,液液相间比界面积大幅度增加,强化了相间的传热传质作用[7]。同时调节电场强度可以控制荷电液滴在离散相液体中的荷电行为以及粒径分布。在离散相液体中,处于电场中的液体分子会出现极化现象,使液液相界面聚集大量电荷,电荷间的库仑斥力削弱界面张力。当液滴的荷电量超过瑞利极限时[8],液滴即发生破碎,导致液液相界面撕裂,离散相液体会进一步出现二次破碎,产生大量微米、亚微米级尺度的荷电液滴。同时由于液滴间库仑斥力的作用,荷电液滴很难聚并,液滴群保持良好的单分散状态[9-10]。液滴在离散相液体中破碎成为细小液滴群有利于形成乳化液,从而有效增强相间的混合效果。另一方面,在石油开采、萃取等领域为避免离散相液滴的破碎和分散过程,常利用外加电场达到离散相液滴聚并和沉降的效果[11-12]。离散相液滴在连续相中的变形、破碎和分散过程是这些工业领域的基本特点,有必要对电场作用下离散相液滴的荷电行为演变过程进行深入研究。
在以静电喷雾为代表的气液两相体系中,荷电液滴在电场作用下产生变形和破碎,在管口处形成锥形的泰勒锥射流[13],在泰勒锥的末端形成细小的微液滴群,广泛应用于喷墨打印、静电喷涂等领域。气液两相体系中的荷电液滴喷雾研究为液液两相系统中的荷电分散过程提供了理论基础[8-13]。研究者通过模拟和实验方法对液液相界面[14]、离散相破碎模式[15-16]、液滴聚并[11-17]等开展相关研究,获得了电场强度和液体性质等因素对单液滴荷电行为的初步影响规律。但对荷电液液两相分散系统中离散相液滴的显微形貌特征有待于深入研究,以揭示电场对荷电液滴变形破碎发展过程和小液滴形成的影响机制,从而利用电场控制离散相液滴在另一不相溶相中的荷电分散过程,强化液液相间混合效果。
本文设计了不相溶醇油两相荷电分散破碎实验台,利用高速摄像与显微成像技术对不断注入连续相中的液滴荷电变形演变过程开展可视化研究,捕捉不同电场强度下荷电液滴的变形、破碎等现象的显微形貌特征与演变细节,得到液滴粒径与电压和流量的关系和荷电液滴粒径分布规律,讨论荷电液滴分散破碎过程的特征。
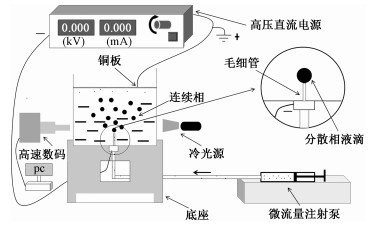
1 实验装置与方法图 1为醇在不相溶油相中的荷电分散实验装置示意图,反应器采用100 mm×30 mm×100 mm的有机玻璃容器,容器底部固定一不锈钢毛细管,毛细管与容器绝缘连接,毛细管内外径分别为0.4和0.7 mm。离散相液体通过毛细管自容器底部注入,其流量由微流量注射泵精确控制。不锈钢毛细管与高压直流电源负极相连,容器上部水平布置板状电极并接地,构成一定间距的针-板式负高压接触荷电电场区域。
|
Download:
|
| 图 1 醇在油相中荷电分散实验装置图 Fig. 1 Experimental setup | |
采用型号为Phantom V1611的显微高速数码摄像机,配合12倍变焦显微镜头进行显微拍摄。借助显微镜头可以捕捉液体荷电行为微细局部结构特征。以5 000 fps的频率精确捕捉不同电场强度下乙醇液体荷电行为演变过程的显微形貌特征并记录以备后期分析处理。拍摄背景光源为高亮LED冷光源,放置在高速数码相机的对面和不锈钢毛细管口正对,以便能在极短的曝光时间内观察到比较清晰的图像。为便于可视化研究,选择透光性较好的分析级乙醇和大豆油作为实验介质,实验前在容器内放置一定量大豆油。通过微流量注射泵精确控制离散相的流动速度,并可通过调节高压直流电源参数,得到不同荷电电压下乙醇液体的荷电行为演变过程。实验采用的大豆油和乙醇的物性参数如表 1所示。实验环境温度控制在(20±0.5) ℃。
|
|
表 1 实验介质的物性参数 Table 1 Physical parameters of medium used in the experiment |
乙醇流量较低时,随微流量注射泵不断注入液体,不锈钢管口处液体在表面张力作用下聚集形成球状液滴。脱离管口的球形液滴沿毛细管轴线方向向上运动,形成一系列粒径单一均匀的球形液滴。这种液滴形成规律被称为单滴模式,随电压增加,液滴的形成过程将依次经历摆动模式、枝杈模式和膜状模式,王军锋等[15-16]已对此进行相关研究,但对液滴的整个形成过程的细节规律未开展深入探讨。外加电场产生的电场力可以影响和改变液滴的形成、变形、分散过程,使荷电液滴在不相溶液相中表现出不同的行为特点。因此液滴的初始形成和变化过程显著影响液滴在连续相中的粒径分布特征和液-液相间的相互作用,决定了相间传热传质效果。
在电场作用下,荷电液滴表面会聚集大量的电荷,液滴自身的表面张力或液液相界面张力被电场力削弱,球形液滴受到扰动,产生不稳定变形。较小电场力作用下,因为液体表面张力降低,球形荷电液滴自身的尺寸会逐渐减小。同时由于液体流量保持稳定,毛细管口处产生液滴的频率会逐渐加快。液滴表面由于聚集了同种电荷而相互排斥,使液滴的运动方向脱离毛细管轴线,出现左右摆动现象,形成沿毛细管轴线对称分布的液滴,即摆动模式,如图 2所示。

|
Download:
|
| 图 2 不同电压下油相中乙醇液滴的摆动模式 Fig. 2 Swing modes of charged droplets at different voltage volues | |
为定量描述荷电液滴在连续相中分散的特征,分别用Re、BoE表征液体流量和荷电电压对实验结果进行分析。Re可通过液体流量Q与毛细管内径di由下式计算得到:
| $R e=\frac{4 \rho Q}{\pi \mu d_{i}}. $ | (1) |
由于荷电液滴的形成过程主要发生在不锈钢毛细管管口附近,因此可用管口附近的电场强度E0[18]表征电压对液滴的影响。对于点板形式的电极分布,当点板距离为H时,管口处电场强度可由荷电电压V与毛细管外半径r利用下式得到:
| $E_{0}=\frac{V}{r \ln \sqrt{\frac{4 H}{r}}}. $ | (2) |
利用管口处电场强度,可以获得表征电应力和毛细力相对大小的无量纲参量BoE[19],用以准确描述荷电液滴的变化特征:
| $B o_{\mathrm{E}}=\frac{\varepsilon r E_{0}^{2}}{\lambda}. $ | (3) |
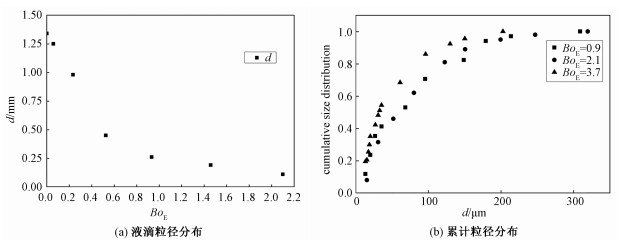
实验中当乙醇流量一定时,液滴粒径分布随电邦德数(BoE)的变化关系和不同电邦德数下的液滴累计粒径分布分别由图 3(a)和3(b)给出。毛细管口处液滴产生频率F随电邦德数BoE的变化趋势如图 4所示。实验结果表明随电压增加,液滴粒径d逐渐下降,小粒径液滴个数不断增加,并且液滴的产生频率显著上升。图 3(a)中电邦德数从0增加到2时,液滴粒径从1.3 mm下降到0.1 mm,比最初的1.3 mm减小92.3%,同时图 4中液滴的产生频率提高近10倍。从图 3(b)中可以得到,不同电邦德数下,粒径小于100 μm的液滴占总液滴数的近70%,且随电邦德数增加,较小粒径的液滴百分比逐渐提高。由于单位时间内产生液体的体积一定,随电邦德数增加,液液相间接触面积随液滴个数增加逐渐上升,更多小液滴分散到油相中。
|
Download:
|
| 图 3 液滴粒径随电邦德数的变化关系 Fig. 3 Relationship between droplet size and BoE | |

|
Download:
|
| 图 4 液滴产生频率随电邦德数变化关系 Fig. 4 Relationship between frequency and BoE | |
为获得液滴产生频率与电邦德数的定量关系,用单位频率对液滴产生频率F无量纲化,无量纲频率f0可由下式得到:
| $f_{0}=\frac{F}{f^{\prime}}. $ | (4) |
式中:f′=1 Hz,表示单位频率。则荷电液滴的无量纲频率f0与电邦德数BoE的数量关系可通过图 4得到,图 4中二者呈线性关系,得到的无量纲频率与电邦德数拟合关系为f0=5.45BoE。
为进一步通过荷电电压控制液滴在连续相中的粒径分布,可通过液体流量和电邦德数定量预测离散相液滴的粒径大小。假设产生的液滴均为球形,单个液滴的体积为Z。液体的流量为Q,即单位时间内产生液体的体积,液滴产生频率F表示单位时间内产生液滴的个数,由于通过毛细管口处的液体体积保持不变,那么Q=Z×F,根据式(4),可计算得到液滴的直径d随电邦德数BoE和流量的变化关系。
| $d=\sqrt[3]{\frac{6 Q}{5.45 \pi f^{\prime} B o_{\mathrm{E}}}}. $ | (5) |
液滴粒径预测模型公式(5)的准确性可由实验结果中获得的液滴粒径d和频率F进行验证。单个液滴的体积Z可通过实验测得的液滴粒径得到。单位时间内产生液滴的数量为f0,液滴体积和频率的乘积应与微流量注射泵的流量值相等。以Re=2时的实验结果进行验证,此时乙醇液体的流量为Q=0.001 mL/s。单位时间内,单个液滴体积Z与液滴频率F的乘积Q′随电邦德数的变化关系如图 5所示。可以看出理论流量Q′在0.001 mL/s附近上下摆动,基本与真实的实验流量相吻合,这也证明了上述液滴粒径模型的准确性。

|
Download:
|
| 图 5 理论液体流量随电邦德数变化关系 Fig. 5 Relationship between theoretical flow rate and BoE | |
随荷电电压增加,液滴表面聚集的电荷逐渐增多,电场力的作用效果增强,液滴不能再保持球形状态而发生形变,当表面电荷量接近瑞利极限时[8],液滴将发生破碎,形成枝杈状破碎。图 6给出的是利用可视化显微高速摄像技术捕捉到的液体枝杈状破碎全过程,图 6(a)是枝杈破碎的整体形态特征,图 6(b)显示的是放大枝杈末端后得到的液滴释放过程的显微形貌特征。图 6(a)中,在主液桥上形成数个形貌特征相似的枝杈,通常产生3个主枝杈,液体通过与毛细管连接的液桥不断输送给各个枝杈,在每个枝杈的末端产生射流,微射流释放的大量微液滴进入连续相中。对枝杈末端进一步放大后,可以得到荷电液滴释放过程的显微细节特征,如图 6(b)所示。枝杈末端的液丝在电场力作用下不断拉伸变细,形成锥形液桥,在液桥末端产生3个与母液桥类似的小液丝,小液丝继续拉伸形成锥形液桥,如此反复,直到液桥所提供的液体不足以形成新的液丝时,液丝的末端发生破碎,释放细小液滴,同时主液桥脱离毛细管口形成较大液滴,整个枝杈进入下一个循环周期。这一过程中,液滴的粒径分布不均匀,产生液滴的粒径范围从几十微米到100多微米,均小于单滴和摆动模式下的液滴粒径,因此此模式下相间作用效果显著增强。但这种液滴破碎模式下液滴粒径分布不均匀,为定量讨论枝杈破碎模式下液滴的粒径分布规律,将采用理论模型Rosin-Rammler函数对荷电液滴尺寸分布进行描述[20],并将结合2.3节液滴在膜状破碎模式下的粒径分布规律进行分析讨论。

|
Download:
|
| 图 6 枝杈破碎模式中荷电液滴形成过程 Fig. 6 Charged droplet formation process in branch mode | |
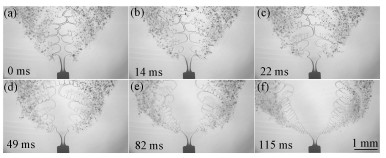
当荷电电压达到一定值时,与毛细管连接的主液桥和主液桥上的枝杈会拉伸扩展成很薄的液膜,并在液膜四周产生许多细小微射流,释放大量微米级液滴,这种液滴形成方式被称为膜状模式,如图 7所示。图 7中从(a)到(f)依次给出的是液桥从枝杈状液膜逐渐过渡到形状类似火焰的锥形液膜的演变过程。随所施加电压的提高,离散相液体获得更多的自由电荷,在电场力作用下各个主液桥和液桥边缘的液丝被拉伸延展变薄成为液膜,同时液膜边缘形成许多细小的微形射流,并释放带有电荷的微小液滴。尽管这些微小液滴的粒径难以准确测量,但通过测量微射流的直径可以间接得到其所释放微小液滴的粒径范围。从图 7(f)中可以测量得到液膜边缘微射流的直径仅在十几微米范围,则从微射流末端释放的小液滴粒径会更小,可达到数微米。可以看出图 7中整个液膜边缘微射流释放的小液滴尺寸微小且粒径分布均匀,这有利于提高不相溶液-液相间的接触面积,从而增强两相间的混合效果,达到强化传热传质的目的。值得注意的是,Swarup等[21]报道一种液膜和小液滴获得方法,在较高压力条件下,两个高流速的液柱通过相互强烈撞击并融合来产生液膜并在液膜边缘产生液丝,以获得毫米级小液滴。与这种采用液柱撞击形成液膜并获得液滴的方法相比,本文提出的通过外加电场形成液膜并释放微小液滴的方法更为高效节能[22-23]。
|
Download:
|
| 图 7 液膜和液滴的形成过程 Fig. 7 Droplet formation process in sheet mode | |
由于枝杈状破碎和本部分膜状破碎模式下,液滴数量较多,通过统计两种模式下的液滴粒径尺寸,采用Rosin-Rammler函数对两种破碎模式下的粒径分布规律进行分析[20],该函数可表示为
| $F(d)=\mathrm{e}^{-\left(d / d_{0}\right)^{m}}. $ | (6) |
式中:F(d)为分布函数;d为液滴粒径尺寸;d0为特征尺寸,约为F(d)=0.368时的粒径值;m为粒径均匀性系数,m越大, 表明雾滴尺寸分布越窄。将式(6)连续取两次对数后可得到
| $\ln (-\ln (1-F(d)))=m \ln d-m \ln d_{0}. $ | (7) |
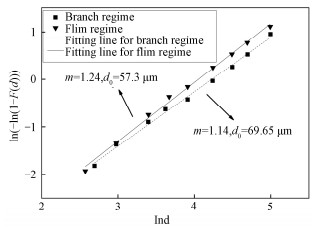
式(7)表明在双对数坐标中,Rosin-Rammler分布为一条直线,m表示直线斜率,mlnd0表示截距。根据式(7)对实验数据进行拟合后可获得枝杈破碎模式和膜状破碎模式下的液滴粒径Rosin-Rammler分布,如图 8所示。由图可见, 两种破碎模式下的实验结果拟合较好,说明这两种破碎模式下液滴粒径分布符合Rosin-Rammler规律。同时,膜状破碎模式下的粒径均匀性系数较大且粒径特征尺寸较小,表明该模式下粒径分布较窄且粒径尺寸小于枝杈破碎模式中的液滴粒径,液滴更加细小。
|
Download:
|
| 图 8 双对数坐标下Rosin-Rammler分布函数 Fig. 8 Rosin-Rammler distribution function in double logarithmic coordinates | |
通过式(6)可得到Rosin-Rammler分布函数的密度函数,即液滴粒径分布密度:
| $f(d)=\frac{m}{d_{0}} \times d^{m-1} \times \mathrm{e}^{-\left(d / d_{0}\right)^{m}}. $ | (8) |
在枝杈和膜状破碎模式下液滴粒径密度分布如图 9所示,在枝杈破碎模式下, 粒径谱相对较宽。膜状破碎模式下,密度曲线的峰值增大,即雾滴尺度变小, 分布变窄。此外, 两种破碎模式下荷电液滴的尺寸分布呈现明显的不对称性, 概率密度曲线的峰值偏左, 即峰值处的滴径要小于平均滴径, 这说明小液滴数量较多而尺寸分布较窄, 大雾滴数较少而尺寸分布较宽。电压较高时,液滴的这两种破碎模式有利于液液相间分散,这是由于在电压较高时, 单位体积的液滴带电量增大, 一些尺寸大的雾滴会发生二次破碎, 从而产生大量尺寸较小的液滴,使液滴分布变窄, 总体滴径分布更加均匀。

|
Download:
|
| 图 9 液滴粒径密度分布 Fig. 9 Droplet size density distribution | |
本文基于显微高速摄像技术通过实验研究电场作用下荷电乙醇液滴在油相中变形破碎现象的显微形貌特征和小液滴产生过程的细节演变机制。根据实验结果,定量分析得到液滴粒径分布规律和生成频率随荷电邦德数的变化关系,发现液滴粒径随电邦德数的增加而显著下降,液滴的生成频率随电邦德数提高而明显上升。给出低电压条件下球形液滴的粒径与流量和电邦德数的数量关系,表明液滴粒径主要受离散相流量和电邦德数影响,通过调节液体流量和荷电电压可以控制液滴的粒径大小。当电压较高时,离散相液滴会发生剧烈的变形和破碎,产生大量尺寸较小的液滴,并且小液滴主要通过位于枝杈末端和液膜边缘的微射流形成,液-液相间接触面积显著增加。荷电液滴在枝杈和膜状破碎模式下的液滴粒径分布符合Rosin-Rammler函数,且粒径分布细小均匀。因此在外加电场作用下不相溶液-液相分散过程会显著增强,有利于强化相间作用并增强传质传热效果。
| [1] |
Kockmann N, Roberge D M. Scale-up concept for modular microstructured reactors based on mixing, heat transfer, and reactor safety[J]. Chemical Engineering and Processing:Process Intensification, 2011, 50(10): 1017-1026. Doi:10.1016/j.cep.2011.05.021 |
| [2] |
Lai F C, Jiri J K, Suzana Y, et al. Kinetic studies on waste cooking oil into biodiesel via hydrodynamic cavitation[J]. Journal of Cleaner Production, 2017, 146: 47-56. Doi:10.1016/j.jclepro.2016.06.187 |
| [3] |
Graaf S van der, Schroën C G P H, Sman R G M van der, et al. Influence of dynamic interfacial tension on droplet formation during membrane emulsification[J]. Journal of Colloid and Interface Science, 2004, 277(2): 456-463. Doi:10.1016/j.jcis.2004.04.033 |
| [4] |
Federico A, Davide D, Romain E, et al. Influence of DC electric field upon the production of oil-in-water-in-oil double emulsions in upwards mm-scale channels at low electric field strength[J]. Experimental Thermal and Fluid Science, 2017, 81: 265-276. Doi:10.1016/j.expthermflusci.2016.10.023 |
| [5] |
Wang B B, Wang X D, Wang T H, et al. Electro-coalescence of two charged droplets under constant and pulsed DC electric fields[J]. International Journal of Heat and Mass Transfer, 2016, 98: 10-16. Doi:10.1016/j.ijheatmasstransfer.2016.02.083 |
| [6] |
Seyed-Yagoobi J, Bryan J E. Enhancement of heat transfer and mass transport in single-phase and two-phase flows with electrohydrodynamics[J]. Advances in Heat Transfer, 1999, 33: 95-186. Doi:10.1016/S0065-2717(08)70304-6 |
| [7] |
Eastwood C D, Armi L, Lasheras J C. The breakup of immiscible fluids in turbulent flows[J]. Journal of Fluid Mechanics, 2004, 502: 309-333. Doi:10.1017/S0022112003007730 |
| [8] |
Rayleigh L. On the equilibrium of liquid conducting masses charged with electricity[J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1882, 14(87): 184-186. Doi:10.1080/14786448208628425 |
| [9] |
Sato M, Hatori T, Saito M. Experimental investigation of droplet formation mechanisms by electrostatic dispersion in a liquid-liquid system[J]. IEEE Transactions on Industry Applications, 1997, 33(6): 1527-1534. Doi:10.1109/28.649965 |
| [10] |
Ha J W, Yang S M. Breakup of a multiple emulsion drop in a uniform electric field[J]. Journal of Colloid and Interface Science, 1999, 213(1): 92-100. Doi:10.1006/jcis.1999.6117 |
| [11] |
Eow J S, Ghadiri M, Sharif A. Experimental studies of deformation and break-up of aqueous drops in high electric fields[J]. Colloids Surface A, 2003, 225: 193-210. Doi:10.1016/S0927-7757(03)00330-3 |
| [12] |
Mhatre S, Vivacqua V, Ghadiri M, et al. Electrostatic phase separation:a review[J]. Chemical Engineering Research and Design, 2015, 96: 177-195. Doi:10.1016/j.cherd.2015.02.012 |
| [13] |
Taylor G. Disintegration of water drops in an electric field[J]. Proceedings of the Royal Society of London, 1964, 280: 383-397. |
| [14] |
梁坤峰, 贾雪迎, 高春燕, 等. 液-液分散雾化非相溶两相流界面追踪模拟[J]. 农业机械学报, 2015, 46(6): 364-371. |
| [15] |
王军锋, 孙成仁, 霍元平, 等. 醇在油相中荷电雾化的实验研究[J]. 工程热物理学报, 2016, 37(7): 1469-1474. |
| [16] |
王东保, 王军锋, 刘海龙, 等. 电场强化酯交换过程中醇油两相分散特性研究[J]. 工程热物理学报, 2017, 38(12): 2641-2645. |
| [17] |
Eow J S, Ghadiri M, Sharif A. Deformation and break-up of aqueous drops in dielectric liquids in high electric fields[J]. Journal of Electrostatics, 2001, 51: 463-469. |
| [18] |
Coelho R, and Debeau J. Properties of the tip-plane configuration[J]. Journal of Physics D:Applied Physics, 1971, 4(9): 1266-1280. Doi:10.1088/0022-3727/4/9/305 |
| [19] |
Reznik, S N, Yarin, A L, Theron A, et al. Transient and steady shapes of droplets attached to a surface in a strong electric field[J]. Journal of Fluid Mechanics, 2004, 516(516): 349-377. |
| [20] |
Macias G A, Cuerda-Correa E M, Diaz-Diez M A. Application of the Rosin-Rammler and Gates-Gaudin-Schuhmann models to the particle size distribution analysis of agglomerated cork[J]. Materials Characterization, 2004, 52(2): 159-164. Doi:10.1016/j.matchar.2004.04.007 |
| [21] |
Swarup Y J, Geetanjali Y, Mishra, D P. Visualizations of sheet breakup of non-Newtonian gels loaded with nanoparticles[J]. International Journal of Multiphase Flow, 2017, 100: 57-76. |
| [22] |
Shrimpton J S. Charge injection systems[M]. Berlin, Heidelberg: Springer-Verlag Press, 2009: 183-184.
|
| [23] |
Hokmabad B V, Faraji S, Dizajyekan T G, et al. Electric field-assisted manipulation of liquid jet and emanated droplets[J]. International Journal of Multiphase Flow, 2014, 65: 127-137. Doi:10.1016/j.ijmultiphaseflow.2014.03.009 |
 2020, Vol. 37
2020, Vol. 37 


